2.4有理数的除法

(共16张PPT)
教学目标：
1.经历根据除法是乘法的逆运算，归纳出有理数的除法法则的过程.
2.掌握有理数除法法则，理解零不能做除数.
3.理解除法转化为乘法，体验矛盾着的对立双方在一定的条件下互相转化的辨证唯物主义思想.
4.会运用除法法则求两个有理数的商，会进行简单的混合运算.
教学重点：
除法法则和除法运算.
教学难点：
根据除法是乘法的逆运算，归纳出除法法则.
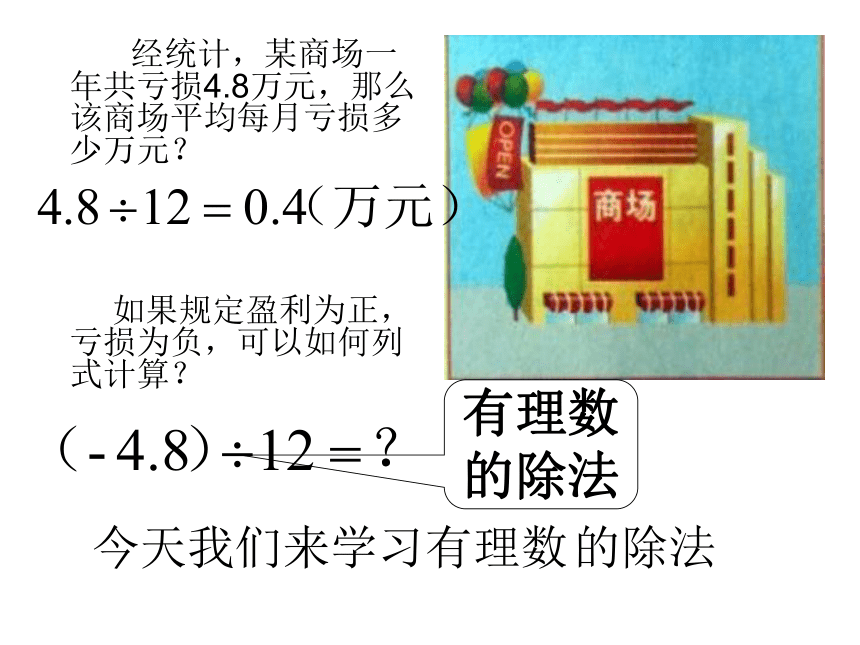
经统计，某商场一年共亏损4.8万元，那么该商场平均每月亏损多少万元？
如果规定盈利为正，亏损为负，可以如何列式计算？
有理数
的除法
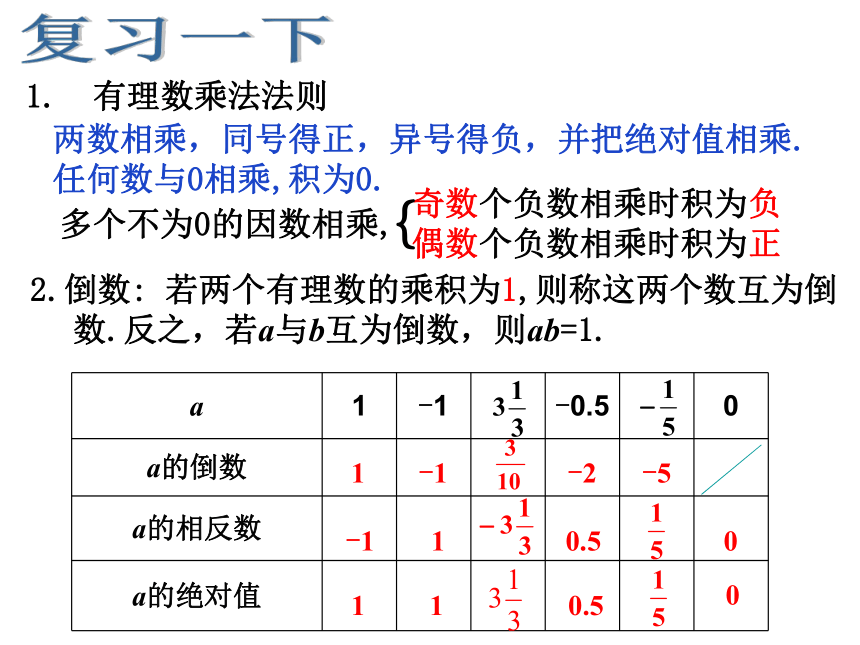
两数相乘，同号得正，异号得负，并把绝对值相乘.
任何数与0相乘,积为0.
1. 有理数乘法法则
奇数个负数相乘时积为负
偶数个负数相乘时积为正
多个不为0的因数相乘,
2.倒数: 若两个有理数的乘积为1,则称这两个数互为倒数.反之，若a与b互为倒数，则ab=1.
a 1 -1 -0.5 0
a的倒数
a的相反数
a的绝对值
1
-1
-2
-5
-1
1
1
0.5
0
0.5
1
0
｛
我们知道，对正有理数而言，除法是乘法的逆运算.例如，从3×2=6可得6÷3=2或6÷2=3.
对一般地有理数，除法也是乘法的逆运算.所以，12×（-0.4）=-4.8可得（-4.8）÷12=-0.4.
填空：
（1）由9×（-2）=-18，得
（-18）÷（-2）=（ ），（-18）÷9=（ ）.
（2）由（-9）×2 =-18，得
（-18）÷2=（ ），（-18）÷（-9）=（ ）.
（3）由（-9）×（-2）=18，得
18÷（-2）=（ ）， 18÷（-9）=（ ）.
（4）由0×a=0（a表示不等于零的有理数），得
0÷a=（ ）.
观察上面的结果，两个有理数相除，商的符号有什么规律？商的绝对值呢？
做一做 ZUOYIZUO
9
-2
-9
2
-9
-2
0
并把绝对值相除；
0÷a=____,
0
零除以任何非零数得零
有理数的除法法则：
两数相除，同号得正，异号得负，并把绝对值相除；0除以任何一个不等于0的数都得0.
注意： 0不能做除数.
你能利用除法是乘法的逆运算来说明除以一个数等于乘以这个数的倒数吗？
解：
探究
结论：除以一个数（不等于0），等于乘上这个数的倒数.
例1 计算
（1）（-8）÷（-4）.
（2）（-3.2）÷0.08.
（3）
解 （1）（-8）÷（-4）=+（8÷4）=2.
（2）（-3.2）÷0.08=-（3.2÷0.08）=-40.
（3）
一般地，有理数的乘法与除法之间有以下关系：
除以一个数（不等于0），等于乘这个数的倒数.
一般步骤：1.确定商的符号
2.绝对值相除
3.有时需把除法转化为乘法
注意:规范解题格式
(1) 120÷40 =
(2) (－21) ÷3=
(3) (－36) ÷(－ 9)=
(4)( － 24 ） ÷8=
(5) (－ 56 ）÷（ － 8）=
(6)96 ÷(－4)=
(7)7.5 ÷(－2.5)=
(8) =
－ 7
3
4
－24
－3
7
－ 3
－36
(1)
(2)
例2 计算
解（1）
（2）
除法没有
结合律
A. 任何一个数都有倒数
B. 一个数的倒数小于这个数
C. 0除以任何一个数商都是0
D. 两数商为0则只有被除数为0
D
1.两个数的商是正数,那么这两个数是( )
A.和为正 B.和为负 C.积为正 D.异号
2.下列说法正确的是（ ）
C
3.下列计算是否正确，若不正确，请指出，并改正。
除法没有
结合律
4.列式计算：
（1）-3与-2的和的倒数.
（2）-3与-2的倒数和.
（3）-3与-2的倒数的和.
4.若a, b互为倒数, 则ab=____
1
5.若a, b互为相反数, 且a、b不为0，则a+b=____，
0
-1
0
7. 则
则