4.2平行四边形及其性质(3) 课件 浙教版数学八年级下册
文档属性
| 名称 | 4.2平行四边形及其性质(3) 课件 浙教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 814.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-25 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
八 年 级 数学 下 册
《4.2平行四边形及其性质》
(第三课时)
新课导入
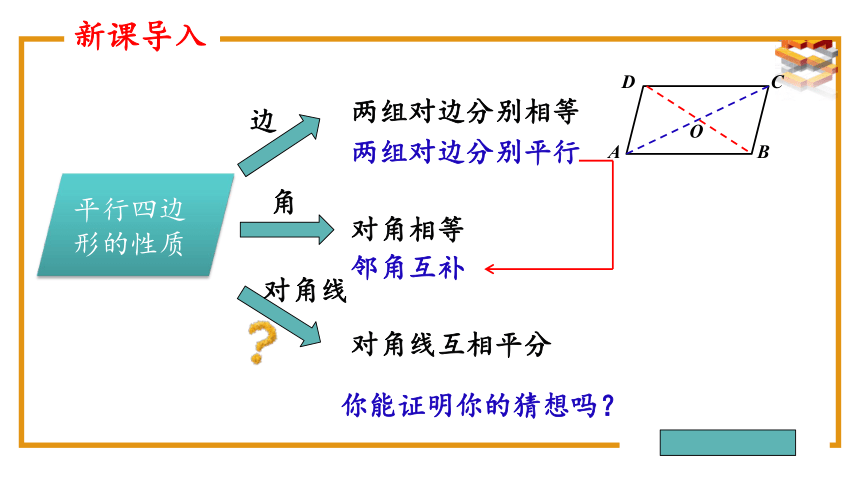
平行四边形的性质
角
边
对角线
两组对边分别相等
对角相等
对角线互相平分
D
A
B
C
O
你能证明你的猜想吗?
两组对边分别平行
邻角互补
求证: OA=OC,OB=OD.
∴∠1=∠2,∠3=∠4
又∵AD=BC(平行四边形的对边相等)
∴ △AOD≌ △COB(ASA)
∴OA=OC,OB=OD
探索新知
D
A
B
C
O
已知:如图,在 ABCD中,对角线AC,BD相交于点O.
在 ABCD中,
AD∥BC(平行四边形的定义)
2
1
3
4
思考:由已知条件你能得到什么结论?
证明:
AB∥CD,AB=CD
AD∥BC,AD=BC
∠ABC=∠CDA
∠DAB=∠BCD
D
A
B
C
O
2
2
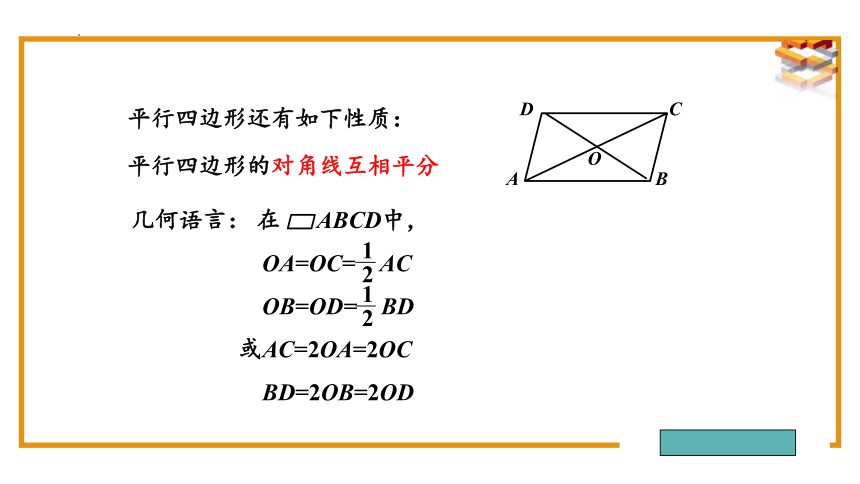
几何语言: 在 ABCD中,
OA=OC= AC
OB=OD= BD
或AC=2OA=2OC
BD=2OB=2OD
1
1
平行四边形还有如下性质:
平行四边形的对角线互相平分
小试牛刀
D
A
B
C
O
如图,在 ABCD中,AC与BD相交于点O,
(1)若AC=24cm,BD=18cm,则AO=______BO=______
又若AB=13cm,则△COD的周长为______
(2)若△AOB的周长为30cm,AB=12cm,则对角线AC与BD的和是______
(3)若AB=13cm ,△AOB 的周长比△AOD的周长大3cm,则AD=______
12cm
9cm
OA+OB+AB
OA+OD+AD
AB-AD
10cm
OA+OB+AB=30
即:OA+OB=18
36cm
34cm
12
9
25
9
12
13
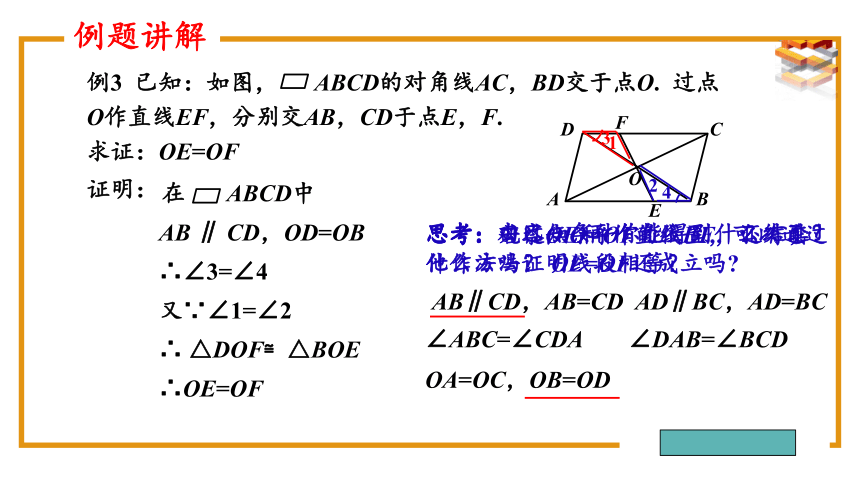
∴∠3=∠4
又∵∠1=∠2
∴ △DOF≌△BOE
∴OE=OF
AB ∥ CD,OD=OB
例3 已知:如图, ABCD的对角线AC,BD交于点O. 过点O作直线EF,分别交AB,CD于点E,F.
求证:OE=OF
D
A
B
C
O
F
E
思考:观察OE和OF的位置,可以通过什么方法证明线段相等?
思考:由已知条件你能得到什么结论?
例题讲解
在 ABCD中
证明:
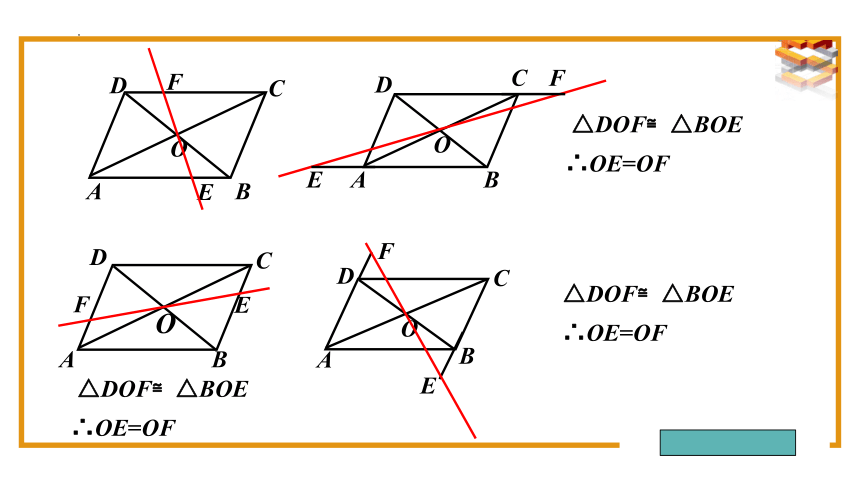
思考:若过点O再作直线EF,还有其他作法吗? OE=OF还成立吗
AB∥CD,AB=CD
AD∥BC,AD=BC
∠ABC=∠CDA
∠DAB=∠BCD
OA=OC,OB=OD
2
1
3
4
A
B
C
D
O
E
F
A
B
C
D
O
F
E
A
B
C
D
O
E
F
A
B
D
O
E
F
C
△DOF≌△BOE
∴OE=OF
△DOF≌△BOE
∴OE=OF
△DOF≌△BOE
∴OE=OF
A
B
C
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
A
B
D
O
E
F
C
思考:这两个部分的面积和周长有什么关系?
思考:结论还成立吗?
相等
仍然成立
你能得到什么结论呢?
过对角线的交点的直线把平行四边形分割成周长和面积相等的两部分
1.一块平行四边形草地中间有一水井在点M处,为了浇水的方便,经过水井修一条小路,并且把草地分成面积相等的两部分,请同学们画出这条小路的位置.
巩固新知
A
B
D
O
C
.M
例4 如图,在 ABCD中,对角线AC,BD交于点E,AC⊥BC,AC=4,AB=5,求BD的长.
A
B
C
D
E
思考:由已知条件你能求得哪些线段的长度?
5
3
4
BC=3
AE=EC=2
2
2
要求BD的长度可以先求哪条线段的长度?为什么?
求出BE的长度,因为平行四边形对角线互相平分,所以BD=2BE
例4 如图,在 ABCD中,对角线AC,BD交于点E,AC⊥BC,AC=4,AB=5,求BD的长.
A
B
C
D
E
5
3
4
2
2
解:∵AC⊥BC,AC=4,AB=5
∴BC=3
在 ABCD中
CE= AC=2
2
1
在 ABCD
∴BD=2BE=
∴
还有别的方法吗?
例4 如图,在 ABCD中,对角线AC,BD交于点E,AC⊥BC,AC=4,AB=5,求BD的长.
A
B
C
D
E
5
3
4
思考:可以用勾股定理直接求出BD的长度吗?
如何添加辅助线构造直角三角形?
F
你能求出CF和DF的长度吗?
3
3
4
请同学们把过程梳理出来.
例4 如图,在 ABCD中,对角线AC,BD交于点E,AC⊥BC,AC=4,AB=5,求BD的长.
A
B
C
D
E
5
3
4
F
3
3
4
解:过点D作DF∥AC交BC的延长线于点F
∵ AC⊥BC, DF∥AC
∴ DF⊥BF
∵AC=4,AB=5
∴ BC=3
AD=BC=3, AD∥BC
即AD∥CF
又∵DF∥AC
在 ABCD中
∴四边形ACFD是平
行四边形
∴DF=AC=4
CF=AD=3
∴BF=6
∵ DF⊥BF
∴
已知:如图, ABCD的对角线AC,BD相交于点O,点E,F分别在AO,CO上,且AE=CF.
求证:∠EBO=∠FDO.
∵ AE=CF
又∵∠AOB=∠COD
∴ △DOF≌△BOE
∴ ∠EBO=∠FDO
OA=OC,OD=OB
在 ABCD中
证明:
∴OA-AE=OC-CF
即OE=OF
思考:在平行四边形里,通常采取什么方法去证明线段相等或者角相等?
三角形全等
AB∥CD,AB=CD
AD∥BC,AD=BC
∠ABC=∠CDA
∠DAB=∠BCD
OA=OC,OB=OD
巩固新知
课堂小结
平行四边形
角
边
对角线
两组对边分别相等
对角相等
对角线互相平分
两组对边分别平行
邻角互补
八 年 级 数学 下 册
《4.2平行四边形及其性质》
(第三课时)
新课导入
平行四边形的性质
角
边
对角线
两组对边分别相等
对角相等
对角线互相平分
D
A
B
C
O
你能证明你的猜想吗?
两组对边分别平行
邻角互补
求证: OA=OC,OB=OD.
∴∠1=∠2,∠3=∠4
又∵AD=BC(平行四边形的对边相等)
∴ △AOD≌ △COB(ASA)
∴OA=OC,OB=OD
探索新知
D
A
B
C
O
已知:如图,在 ABCD中,对角线AC,BD相交于点O.
在 ABCD中,
AD∥BC(平行四边形的定义)
2
1
3
4
思考:由已知条件你能得到什么结论?
证明:
AB∥CD,AB=CD
AD∥BC,AD=BC
∠ABC=∠CDA
∠DAB=∠BCD
D
A
B
C
O
2
2
几何语言: 在 ABCD中,
OA=OC= AC
OB=OD= BD
或AC=2OA=2OC
BD=2OB=2OD
1
1
平行四边形还有如下性质:
平行四边形的对角线互相平分
小试牛刀
D
A
B
C
O
如图,在 ABCD中,AC与BD相交于点O,
(1)若AC=24cm,BD=18cm,则AO=______BO=______
又若AB=13cm,则△COD的周长为______
(2)若△AOB的周长为30cm,AB=12cm,则对角线AC与BD的和是______
(3)若AB=13cm ,△AOB 的周长比△AOD的周长大3cm,则AD=______
12cm
9cm
OA+OB+AB
OA+OD+AD
AB-AD
10cm
OA+OB+AB=30
即:OA+OB=18
36cm
34cm
12
9
25
9
12
13
∴∠3=∠4
又∵∠1=∠2
∴ △DOF≌△BOE
∴OE=OF
AB ∥ CD,OD=OB
例3 已知:如图, ABCD的对角线AC,BD交于点O. 过点O作直线EF,分别交AB,CD于点E,F.
求证:OE=OF
D
A
B
C
O
F
E
思考:观察OE和OF的位置,可以通过什么方法证明线段相等?
思考:由已知条件你能得到什么结论?
例题讲解
在 ABCD中
证明:
思考:若过点O再作直线EF,还有其他作法吗? OE=OF还成立吗
AB∥CD,AB=CD
AD∥BC,AD=BC
∠ABC=∠CDA
∠DAB=∠BCD
OA=OC,OB=OD
2
1
3
4
A
B
C
D
O
E
F
A
B
C
D
O
F
E
A
B
C
D
O
E
F
A
B
D
O
E
F
C
△DOF≌△BOE
∴OE=OF
△DOF≌△BOE
∴OE=OF
△DOF≌△BOE
∴OE=OF
A
B
C
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
A
B
D
O
E
F
C
思考:这两个部分的面积和周长有什么关系?
思考:结论还成立吗?
相等
仍然成立
你能得到什么结论呢?
过对角线的交点的直线把平行四边形分割成周长和面积相等的两部分
1.一块平行四边形草地中间有一水井在点M处,为了浇水的方便,经过水井修一条小路,并且把草地分成面积相等的两部分,请同学们画出这条小路的位置.
巩固新知
A
B
D
O
C
.M
例4 如图,在 ABCD中,对角线AC,BD交于点E,AC⊥BC,AC=4,AB=5,求BD的长.
A
B
C
D
E
思考:由已知条件你能求得哪些线段的长度?
5
3
4
BC=3
AE=EC=2
2
2
要求BD的长度可以先求哪条线段的长度?为什么?
求出BE的长度,因为平行四边形对角线互相平分,所以BD=2BE
例4 如图,在 ABCD中,对角线AC,BD交于点E,AC⊥BC,AC=4,AB=5,求BD的长.
A
B
C
D
E
5
3
4
2
2
解:∵AC⊥BC,AC=4,AB=5
∴BC=3
在 ABCD中
CE= AC=2
2
1
在 ABCD
∴BD=2BE=
∴
还有别的方法吗?
例4 如图,在 ABCD中,对角线AC,BD交于点E,AC⊥BC,AC=4,AB=5,求BD的长.
A
B
C
D
E
5
3
4
思考:可以用勾股定理直接求出BD的长度吗?
如何添加辅助线构造直角三角形?
F
你能求出CF和DF的长度吗?
3
3
4
请同学们把过程梳理出来.
例4 如图,在 ABCD中,对角线AC,BD交于点E,AC⊥BC,AC=4,AB=5,求BD的长.
A
B
C
D
E
5
3
4
F
3
3
4
解:过点D作DF∥AC交BC的延长线于点F
∵ AC⊥BC, DF∥AC
∴ DF⊥BF
∵AC=4,AB=5
∴ BC=3
AD=BC=3, AD∥BC
即AD∥CF
又∵DF∥AC
在 ABCD中
∴四边形ACFD是平
行四边形
∴DF=AC=4
CF=AD=3
∴BF=6
∵ DF⊥BF
∴
已知:如图, ABCD的对角线AC,BD相交于点O,点E,F分别在AO,CO上,且AE=CF.
求证:∠EBO=∠FDO.
∵ AE=CF
又∵∠AOB=∠COD
∴ △DOF≌△BOE
∴ ∠EBO=∠FDO
OA=OC,OD=OB
在 ABCD中
证明:
∴OA-AE=OC-CF
即OE=OF
思考:在平行四边形里,通常采取什么方法去证明线段相等或者角相等?
三角形全等
AB∥CD,AB=CD
AD∥BC,AD=BC
∠ABC=∠CDA
∠DAB=∠BCD
OA=OC,OB=OD
巩固新知
课堂小结
平行四边形
角
边
对角线
两组对边分别相等
对角相等
对角线互相平分
两组对边分别平行
邻角互补
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
