浙教版八下 第3章 数据分析初步 单元复习题(含解析)
文档属性
| 名称 | 浙教版八下 第3章 数据分析初步 单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 411.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 00:00:00 | ||
图片预览



文档简介
八下第三章单元复习
一、单选题
1.一组数据-1,2,5,0,3的中位数是( )
A.5 B.2 C.0 D.-1
2.某小学校园足球对22名队员年龄情况如下:
年龄/岁 9 10 11 12
人数 2 6 10 4
则这个队队员年龄的众数和中位数分别是( )
A.11,10 B.10,11 C.10,9 D.11,11
3.一组数据:5,7,10,5,7,5,6,这组数据的众数和中位数分别是( )
A.10和7 B.5和7 C.6和7 D.5和6
4.某中学为了组建校级篮球队,从七年级开始开设了篮球选修课,12名同学被分成甲、乙两组进行训练,他们的身高(单位:cm)如下表所示:
队员1 队员2 队员3 队员4 队员5 队员6
甲组 156 157 155 156 157 155
乙组 158 155 150 154 163 156
设两队队员身高的平均数依次为 , ,方差依次为 , ,下列关系中完全正确的是( )
A. = , >
B. = , <
C. < , <
D. > , >
5.甲、乙两名学生的十次数学考试成绩的平均分分别是145和146,成绩的方差分别是8.5和60.5,现在要从两人中选择一人参加数学竞赛,下列说法正确的是( )
A.甲、乙两人平均分相当,选谁都可以
B.乙的平均分比甲高,选乙
C.乙的平均分和方差都比甲高,选乙
D.两人的平均分相当,甲的方差小,成绩比乙稳定,选甲
6.某学校为了了解本校学生暑期参加劳动教育活动情况,随机调研了八年级的学生在暑期参加劳动教育活动的天数.如图,请根据图中提供的信息判断在这次抽样调查中,众数和中位数分别是( )
A.5,6 B.5,7 C.6,7 D.7,6
7.小茗同学对5月1日至7日的最高气温进行统计分析制作成统计图(如图所示),下列说法错误的是( )
A.中位数是33℃
B.众数是33℃
C.平均数是
D.4日至5日最高气温下降幅度较大
8.某气象台报告一周中白天的气温(单位:℃)为:3,4,0,3,1,-1,-3,这一周内白天温度的标准差(精确到0.1)是( )
A.2.1 B.2.2 C.2.3 D.2.4
9.为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断( )
①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150﹣180之间;
④该市居民家庭年用水量的平均数不超过180.
A.①③ B.①④ C.②③ D.②④
10.根据下表中的信息解决问题:
数据 37 38 39 40 41
频数 8 4 5 a 1
若该组数据的中位数不大于38,则符合条件的正整数a的取值共有( )
A.3个 B.4个 C.5个 D.6个
二、填空题
11.为选拔一名选手参加全国中学生游泳锦标赛自由泳比赛,我市四名中学生参加了男子100米自由泳训练,他们成绩的平均数 及其方差s2如下表所示:
甲 乙 丙 丁
1′05″33 1′04″26 1′04″26 1′07″29
s2 1.1 1.1 1.3 1.6
如果选拔一名学生去参赛,应派 去.
12.甲、乙两人进行射击测试,每人10次射击成绩的平均数都是9环,方差分别是:,,则射击成绩较稳定的是 .(填“甲”或“乙”)
13.我市体育中考有必考和选考项目,掷实心球是必考项目之一,在一次训练中,张华同学掷实心球10次的成绩依次是(单位:米)7.6,8.5,8.6,8.5,9.1,8.5,8.4,8.6,9.2,73.则张华同学撰实心球成绩的众数是 .
14.某学校九(1)班40名同学的期中测试成绩分别为 , , ,……, .已知 + + +……+ = 4800,y= + + +……+ ,当y取最小值时, 的值为 .
15.一组数据为1,3,5,12,a,其中整数a是这组数据的中位数,则该组数据的平均数是 .
三、解答题
16.某公司欲招聘一名工作人员,对甲、乙两位应聘者进行面试和笔试,他们的成绩(百分制)如表所示.
应聘者 面试 笔试
甲 87 90
乙 91 82
若公司分别赋予面试成绩和笔试成绩6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?
17.某校为了充实师资力量,决定招聘一位数学教师,对应聘者进行笔试和试讲两项综合考核,根据重要性,笔试成绩占30%,试讲成绩占70%.应聘者张颖、李默两人的得分如下表,如果你是校长,你会录用谁?请说明理由.
姓名 笔试 试讲
张颖 78分 94分
李默 92分 80分
18.光明中学数学活动小组为了调查居民的用水情况,从某社区的500户家庭中随机抽取了20户家庭的月用水量,结果如下表所示
月用水量(吨)
10
15 20 25
户数
8
6 4
2
(1)求这20户家庭月用水量的平均数、众数和中位数;
(2)根据上述数据,试估计该社区的月用水量.
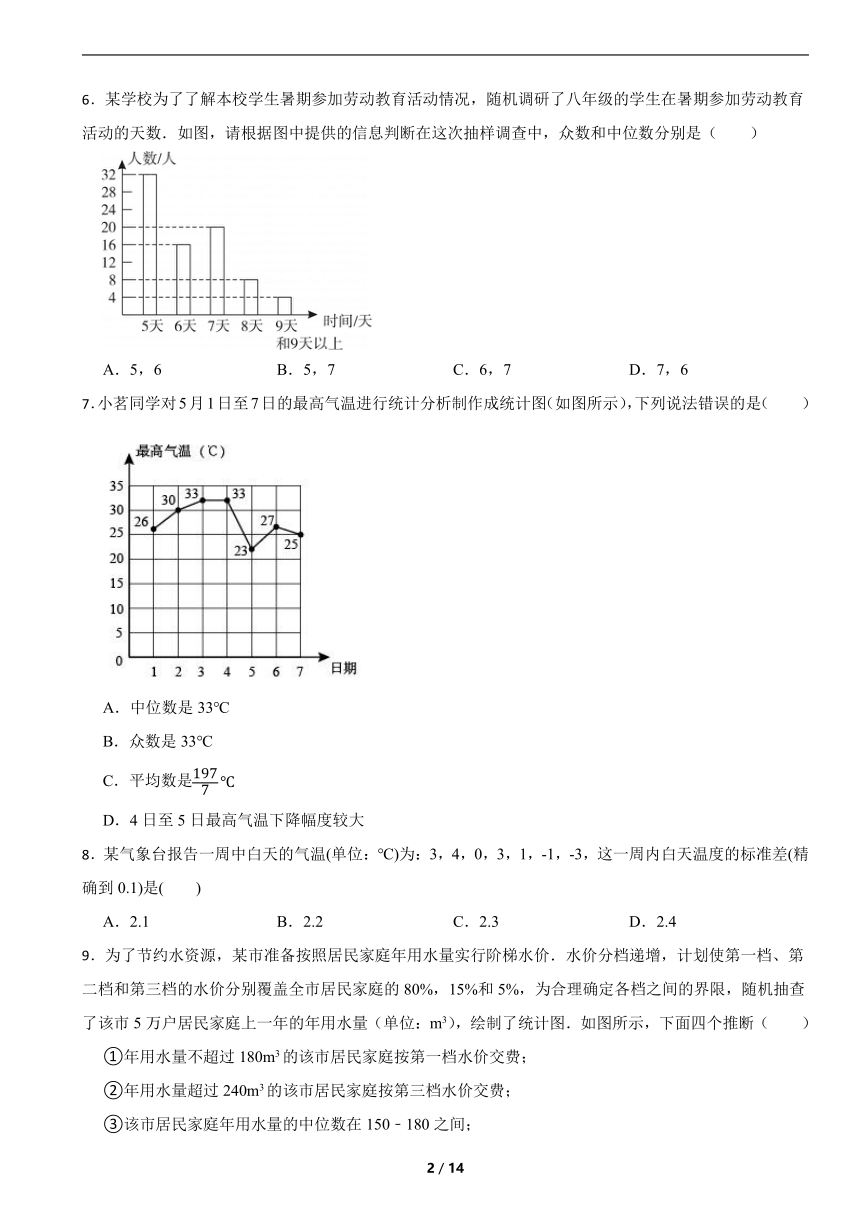
19.甲、乙两名队员参加射击训练,每人射击10次,成绩分别如下:根据以上信息,整理分析数据如下:
平均成绩/环 中位数/环 众数/环 方差
甲 a 7 7 1.2
乙 7 b 8 c
(1) , , .
(2)填空:(填“甲”或“乙”).
从中位数的角度来比较,成绩较好的是 ;从众数的角度来比较,成绩较好的是 ;成绩相对较稳定的是 .
(3)从甲、乙两名队员中选一名队员参加比赛,选谁更合适,为什么?
四、综合题
20.某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实,数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这
三个数中最小的数,例如M{1,2,9}= ,min{1,2,-3}=-3,
min(3,1,1}=1.请结合上述材料,解决下列问题:
(1)①MM{(-2)2,22,-22}= ,
②min{sin300,cos600,tan450}= ;
(2)若min(3-2x,1+3x,-5}=-5,则x的取值范围为 ;
(3)若M{-2x,x2,3}=2,求x的值;
(4)如果M{2,1+x,2x}=min{2,1+x,2x},求x的值.
21.“走进数学世界,感受完美生活.”为增进全体学生对数学文化的了解,临海学校组织了趣味数学知识竞赛,随机抽取若干名学生的成绩,对数据进行整理和分析,现将抽取的学生成绩用(分)表示,并将调查数据分成四组:A.,B.,C.,D.,其中A组分数段内,所有学生得分各不相同,B组学生的成绩分别为:86、86、88、86、83、86.
根据调查数据绘制了以下不完整的统计图:
根据图中信息回答下列问题:
(1)本次共抽查了 名学生,请补全条形统计图;
(2)扇形统计图中,C组所对应的圆心角的度数为 ;
(3)本次抽查的学生成绩的众数为 ,中位数为 ;
(4)竞赛成绩超过80分视作优秀,若该校有2400名学生,根据抽样调查结果,估计该校有 名学生获得优秀.
五、实践探究题
22.甲、乙两支运动队各有10名队员,他们的年龄分布情况分别如图、表所示:
甲、乙两队队员年龄统计表
平均数(近似值) 众数 中位数
甲队 a ① ②
乙队 20 ③ b
解决下列问题:
(1)求甲队队员的平均年龄a的值.(结果取整数)
(2)补全统计表中的①②③三处.
(3)阅读理解-----扇形图中求中位数的方法.
[阅读与思考]
小明同学在求乙队队员年龄的中位数b时,是这样思考的:因为中位数是将一组数据按大小排序后,排在中间位置的一个数或中间两个数的平均数,那就需要先找到数据按大小排序后,大致排在50%附近的数,再根据中位数的概念进行细化求解.
图2这个扇形图中的数据18~21是按大小顺序旋转排列的,我们就可以像图3所示的这样,先找到最大数据“21”与最小数据“18”的分界半径OM,为找到排在50%附近的数,再作出直径MN,那么射线ON指向的数据就是中位数.
王老师的评价:小明的这个方法是从中位数的概念出发,充分利用了扇形图的特性形象直观地解决问题.
[理解与应用]
请你利用小明的方法直接写出统计表中b的值.
答案解析部分
1.【答案】B
【解析】【解答】解:将这组数据按从小到大进行排序为,
则这组数据的中位数为2,
故答案为:B.
【分析】根据中位数的定义计算求解即可。
2.【答案】D
【解析】【解答】解:由表格可得,
这组数据的众数是11岁,
中位数是11岁.
故选D.
【分析】根据表格中的数据可以得到这组数据的众数和中位数.
3.【答案】D
【解析】【解答】解:将这组数据按从小到大排列为:5,5,5,6, 7,7,10
∵数据5出现3次,次数最多,
∴众数为:5;
∵第四个数为6,
∴中位数为6,
故答案为:D.
【分析】这组数据中出现次数最多的是5,根据众数的概念,即可得出答案;再将这组数据按从小到大排列,这组数据共有7个,故处于最中间位置的是排在第四的位置,根据中位数的定义即可得出答案。
4.【答案】B
【解析】【解答】解:∵ =(156+157+155+156+157+155)÷6=156(cm),
=(158+155+150+154+163+156)÷6=156(cm),
∴ ,
∵S2甲= [2×(156﹣156)2+2×(157﹣156)2+2×(155﹣156)2]= ,
S2乙= [(158﹣156)2+(155﹣156)2+(150﹣156)2+(154﹣156)2+(163﹣156)2+(156﹣156)2]=15 ,
∴S2甲<S2乙,
故答案为:B
【分析】根据平均数和方差的计算公式,逐个计算即可。
5.【答案】D
【解析】【解答】解:∵甲的方差是8.5,乙的方差是60.5,
∴甲的方差小于乙的方差,
∴甲的成绩比乙稳定;
∵甲、乙的平均成绩分别是145,146,
∴平均分相当;
故选:D.
【分析】根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
6.【答案】A
【解析】【解答】解:将数据从小到大排列,则中位数为6,
由于5天出现的次数最多,故众数为5,
故答案为:A
【分析】根据众数和中位数的定义即可求解。
7.【答案】A
【解析】【解答】7个数从小到大排序为:23,25,26,27,30,33,33
位于中间位置的数为27
中位数为27℃,故A符合题意;
出现次数最多的为33
众数是33℃,故B不符合题意;
平均数为℃,故C不符合题意;
观察图象可知,4日至5日最高气温下降幅度较大,故D不符合题意;
故答案为:A.
【分析】根据中位数、众数、平均数的计算和折线统计图的性质逐项判断即可。
8.【答案】C
【解析】解答:
.
所以 .
故选C
分析:考查标准差的计算公式,代入标准差的计算公式即可.
9.【答案】B
【解析】【解答】解:①由条形统计图可得:年用水量不超过180m3的该市居民家庭一共有(0.25+0.75+1.5+1.0+0.5)=4(万),
×100%=80%,故年用水量不超过180m3的该市居民家庭按第一档水价交费,正确;
②∵年用水量超过240m3的该市居民家庭有(0.15+0.15+0.05)=0.35(万),
∴ ×100%=7%≠5%,故年用水量超过240m3的该市居民家庭按第三档水价交费,故此选项错误;
③∵5万个数据的中间是第25000和25001的平均数,
∴该市居民家庭年用水量的中位数在120﹣150之间,故此选项错误;
④由①得,该市居民家庭年用水量的平均数不超过180,正确,
故选:B.
【分析】利用条形统计图结合中位数的定义分别分析得出答案.此题主要考查了频数分布直方图以及中位数的定义,正确利用条形统计图获取正确信息是解题关键.
10.【答案】C
【解析】【解答】当a=1时,有19个数据,最中间是:第10个数据,则中位数是38;
当a=2时,有20个数据,最中间是:第10和11个数据,则中位数是38;
当a=3时,有21个数据,最中间是:第11个数据,则中位数是38;
当a=4时,有22个数据,最中间是:第11和12个数据,则中位数是38;
当a=5时,有23个数据,最中间是:第12个数据,则中位数是38;
当a=6时,有24个数据,最中间是:第12和13个数据,则中位数是38.5;
故该组数据的中位数不大于38,则符合条件的正整数a的取值共有:5个.
故答案为:C.
【分析】根据中位数的定义先排序,由已知中位数不大于38得出处于中位数以上和以下的数据个数应相等,可分类讨论得出结果.
11.【答案】乙
【解析】【解答】∵x丁>x甲>x乙=x丙,
∴从乙和丙中选择一人参加比赛,
∵S 乙2<S 丙2,
∴选择乙参赛,
故答案是:乙.
【分析】根据方差越小,成绩越稳定可知,选乙参赛.
12.【答案】甲
【解析】【解答】解:∵=0.12,=0.6,
∴<,
∴射击成绩较稳定的是甲.
故答案为:甲.
【分析】方差越小,波动越小,据此即可得出答案.
13.【答案】8.5
【解析】【解答】解:由题意得8.5出现的次数最多,
∴张华同学撰实心球成绩的众数是8.5,
故答案为:8.5
【分析】根据众数的定义结合题意即可求解。
14.【答案】120
【解析】【解答】解:y=40a
2-2(a
1+a
2+a
3+…+a
40)a+a
12+a
22+a
3)
2+…+a
402,
因为40>0,
所以当a=
时,y有最小值.
【分析】 利用完全平方公式得到y=40a2-2(a1+a2+a3+…+a40)a+a12+a22+a3)2+…+a402,则可把y看作a的二次函数,然后根据二次函数的性质求解.
15.【答案】4.8或5或5.2
【解析】【解答】解:若a为数据的中位数,则数字排列在数据中第三个位置上。
当a=3时,平均数为
当a=4时,平均数为=5
当a=5时,平均数为=5.2
故答案为:4.8或5或5.2。
【分析】 找数据中的中位数,需要将数据由小到大进行排列,位于中间的数即为中位数,根据a的不同情况进行分类讨论即可。
16.【答案】解:甲的平均成绩为:(87×6+90×4)÷10=88.2(分),
乙的平均成绩为:(91×6+82×4)÷10=87.4(分),
因为甲的平均分数较高,
所以甲将被录取.
【解析】【分析】根据题意先算出甲、乙两位应聘者的加权平均数,再进行比较,即可得出答案.
17.【答案】解:录用张颖,理由如下:张颖的平均成绩是:=89.2(分),李默的平均成绩是:(分),所以录用张颖.
【解析】【分析】根据加权平均数公式,分别求出两人的平均得分即可.
18.【答案】解:(1)平均数:=1(5吨),众数:∵用水量为10吨的最多,∴众数是10吨;中位数:根据第10,11个数据都是15吨,∴中位数是15吨;(2)∵平均数为15吨,∴该社区的月用水量约为:15×500=7500(吨)。
【解析】【分析】此题主要考查了平均数、众数和中位数的定义以及利用样本估计总体,是初中阶段考查重点题型,同学们应重点掌握。
(1)根据图表中数据即可得出20个数据的平均数、众数和中位数;
(2)利用(1)中所求即可得出该社区的月用水量。
19.【答案】(1)7;7.5;4.2
(2)乙;乙;甲
(3)解:乙
【解析】【解答】 (1)如图:环
故第一空填:7
乙的成绩为(环):3,4,6,7,7,8,8,8,9,10,中位数是第五和第六个数据的平均值,
故第二空填:7.5
根据方差公式:
=4.2
故第三空填:4.2
(3)解:选乙更加合适。从中位数和众数的角度来看,乙成绩较好;甲乙平均成绩都是7环,稳定发挥的夺冠可能性较低, 说明乙超水平发挥的概率高,故选乙更加合适。
【分析】 (1) 掌握平均数、中位数、方差的计算方法; (2) 根据中位数和众数进行分析评价; (3)会根据方差判定数据的稳定性和波动性,但不是稳定性越小越好,要根据目标确定。
20.【答案】(1);
(2)-2≤x≤4
(3)解:i)当x>0时, x2 >-2x, 则得-2x最小,即-2x=2, ∴x=-1, 与假设矛盾,不符合。ii)当x≤0时,x2≤-2x, 得x≥-2, 即-2≤x≤0,x2=2, x=-,符合题意 ;x2≥-2x, 得x≤-2, 即-2x=2, x=-1, 与假设矛盾,不符合题意。综上所述,x=-.
(4)解: ∵ M{2,1+x,2x} =i)当即x≥1时,min{2,1+x,2x}=2 ,则x+1=2, x=1, 符合题意。ii)当即x≤1时,min{2,1+x,2x}=2 ,则x+1=2x, ∴x=1, 符合题意。iii)当即x=1时,min{2,1+x,2x}=2, x+1=x+1, 所以x=1符合题意。综上所述, x=1
【解析】【解答】解:(1)
.
(2)∵min(3-2x,1+3x,-5}=-5,∴解得x≤4且x≥-2,∴-2≤x≤4;
【分析】(1)根据条件给出的算法原理计算即可。
(2)根据 min{a,b,c} 算法是要求最小值,列不等式组,求不等式组的解集即可。
(3)根据新定义算法公式,分情况讨论,求出符合条件的x值。
(4)根据新定义算法公式,分别设最小值,求出x, 再验证是否符合条件。
21.【答案】(1)20C组人数为:(人),补全条形统计图如下:
(2)54
(3)86分;87分
(4)1800
【解析】【解答】解:(1)本次调查的学生为:9÷45%=20(名),
故答案为:20;
(2)扇形统计图中,C组所对应的圆心角的度数为:360°x =54°,
故答案为:54;
(3)∵A组分数段内,所有学生得分各不相同,B组学生的成绩分别为:86、86、88、86、83、86,
∴20名学生成绩中,86出现发的次数最多,故本次抽查的学生成绩的众数为86;
∵把20名学生成绩从小到大排列,排在中间的两个数是86,88,
∴中位数为:,
(4)由题意可得:(名),
即估计该校有1800名学生获得优秀,
故答案为:1800.
【分析】(1)根据统计图中的数据计算求解即可;
(2)用360°乘C组占比即可得答案;
(3)根据中位数和众数的定义计算求解即可;
(4)根据题意求出即可作答。
22.【答案】(1)解:
(2)19;19;19,20,21
(3)解:由题意和图3可得,
【解析】【解答】(2)解:由图1可得,众数是19,中位数是19,
由图2可得,19、20、21一样多且数据最大,则众数是19,20,21,
故答案为:19,19;19,20,21
【分析】(1)由图1可以计算出 a 的值;(2)根据图1和图2可以将表格中空格补充完整;(3)根据题意和图3可以直接写出b的值
1 / 1
一、单选题
1.一组数据-1,2,5,0,3的中位数是( )
A.5 B.2 C.0 D.-1
2.某小学校园足球对22名队员年龄情况如下:
年龄/岁 9 10 11 12
人数 2 6 10 4
则这个队队员年龄的众数和中位数分别是( )
A.11,10 B.10,11 C.10,9 D.11,11
3.一组数据:5,7,10,5,7,5,6,这组数据的众数和中位数分别是( )
A.10和7 B.5和7 C.6和7 D.5和6
4.某中学为了组建校级篮球队,从七年级开始开设了篮球选修课,12名同学被分成甲、乙两组进行训练,他们的身高(单位:cm)如下表所示:
队员1 队员2 队员3 队员4 队员5 队员6
甲组 156 157 155 156 157 155
乙组 158 155 150 154 163 156
设两队队员身高的平均数依次为 , ,方差依次为 , ,下列关系中完全正确的是( )
A. = , >
B. = , <
C. < , <
D. > , >
5.甲、乙两名学生的十次数学考试成绩的平均分分别是145和146,成绩的方差分别是8.5和60.5,现在要从两人中选择一人参加数学竞赛,下列说法正确的是( )
A.甲、乙两人平均分相当,选谁都可以
B.乙的平均分比甲高,选乙
C.乙的平均分和方差都比甲高,选乙
D.两人的平均分相当,甲的方差小,成绩比乙稳定,选甲
6.某学校为了了解本校学生暑期参加劳动教育活动情况,随机调研了八年级的学生在暑期参加劳动教育活动的天数.如图,请根据图中提供的信息判断在这次抽样调查中,众数和中位数分别是( )
A.5,6 B.5,7 C.6,7 D.7,6
7.小茗同学对5月1日至7日的最高气温进行统计分析制作成统计图(如图所示),下列说法错误的是( )
A.中位数是33℃
B.众数是33℃
C.平均数是
D.4日至5日最高气温下降幅度较大
8.某气象台报告一周中白天的气温(单位:℃)为:3,4,0,3,1,-1,-3,这一周内白天温度的标准差(精确到0.1)是( )
A.2.1 B.2.2 C.2.3 D.2.4
9.为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断( )
①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150﹣180之间;
④该市居民家庭年用水量的平均数不超过180.
A.①③ B.①④ C.②③ D.②④
10.根据下表中的信息解决问题:
数据 37 38 39 40 41
频数 8 4 5 a 1
若该组数据的中位数不大于38,则符合条件的正整数a的取值共有( )
A.3个 B.4个 C.5个 D.6个
二、填空题
11.为选拔一名选手参加全国中学生游泳锦标赛自由泳比赛,我市四名中学生参加了男子100米自由泳训练,他们成绩的平均数 及其方差s2如下表所示:
甲 乙 丙 丁
1′05″33 1′04″26 1′04″26 1′07″29
s2 1.1 1.1 1.3 1.6
如果选拔一名学生去参赛,应派 去.
12.甲、乙两人进行射击测试,每人10次射击成绩的平均数都是9环,方差分别是:,,则射击成绩较稳定的是 .(填“甲”或“乙”)
13.我市体育中考有必考和选考项目,掷实心球是必考项目之一,在一次训练中,张华同学掷实心球10次的成绩依次是(单位:米)7.6,8.5,8.6,8.5,9.1,8.5,8.4,8.6,9.2,73.则张华同学撰实心球成绩的众数是 .
14.某学校九(1)班40名同学的期中测试成绩分别为 , , ,……, .已知 + + +……+ = 4800,y= + + +……+ ,当y取最小值时, 的值为 .
15.一组数据为1,3,5,12,a,其中整数a是这组数据的中位数,则该组数据的平均数是 .
三、解答题
16.某公司欲招聘一名工作人员,对甲、乙两位应聘者进行面试和笔试,他们的成绩(百分制)如表所示.
应聘者 面试 笔试
甲 87 90
乙 91 82
若公司分别赋予面试成绩和笔试成绩6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?
17.某校为了充实师资力量,决定招聘一位数学教师,对应聘者进行笔试和试讲两项综合考核,根据重要性,笔试成绩占30%,试讲成绩占70%.应聘者张颖、李默两人的得分如下表,如果你是校长,你会录用谁?请说明理由.
姓名 笔试 试讲
张颖 78分 94分
李默 92分 80分
18.光明中学数学活动小组为了调查居民的用水情况,从某社区的500户家庭中随机抽取了20户家庭的月用水量,结果如下表所示
月用水量(吨)
10
15 20 25
户数
8
6 4
2
(1)求这20户家庭月用水量的平均数、众数和中位数;
(2)根据上述数据,试估计该社区的月用水量.
19.甲、乙两名队员参加射击训练,每人射击10次,成绩分别如下:根据以上信息,整理分析数据如下:
平均成绩/环 中位数/环 众数/环 方差
甲 a 7 7 1.2
乙 7 b 8 c
(1) , , .
(2)填空:(填“甲”或“乙”).
从中位数的角度来比较,成绩较好的是 ;从众数的角度来比较,成绩较好的是 ;成绩相对较稳定的是 .
(3)从甲、乙两名队员中选一名队员参加比赛,选谁更合适,为什么?
四、综合题
20.某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实,数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这
三个数中最小的数,例如M{1,2,9}= ,min{1,2,-3}=-3,
min(3,1,1}=1.请结合上述材料,解决下列问题:
(1)①MM{(-2)2,22,-22}= ,
②min{sin300,cos600,tan450}= ;
(2)若min(3-2x,1+3x,-5}=-5,则x的取值范围为 ;
(3)若M{-2x,x2,3}=2,求x的值;
(4)如果M{2,1+x,2x}=min{2,1+x,2x},求x的值.
21.“走进数学世界,感受完美生活.”为增进全体学生对数学文化的了解,临海学校组织了趣味数学知识竞赛,随机抽取若干名学生的成绩,对数据进行整理和分析,现将抽取的学生成绩用(分)表示,并将调查数据分成四组:A.,B.,C.,D.,其中A组分数段内,所有学生得分各不相同,B组学生的成绩分别为:86、86、88、86、83、86.
根据调查数据绘制了以下不完整的统计图:
根据图中信息回答下列问题:
(1)本次共抽查了 名学生,请补全条形统计图;
(2)扇形统计图中,C组所对应的圆心角的度数为 ;
(3)本次抽查的学生成绩的众数为 ,中位数为 ;
(4)竞赛成绩超过80分视作优秀,若该校有2400名学生,根据抽样调查结果,估计该校有 名学生获得优秀.
五、实践探究题
22.甲、乙两支运动队各有10名队员,他们的年龄分布情况分别如图、表所示:
甲、乙两队队员年龄统计表
平均数(近似值) 众数 中位数
甲队 a ① ②
乙队 20 ③ b
解决下列问题:
(1)求甲队队员的平均年龄a的值.(结果取整数)
(2)补全统计表中的①②③三处.
(3)阅读理解-----扇形图中求中位数的方法.
[阅读与思考]
小明同学在求乙队队员年龄的中位数b时,是这样思考的:因为中位数是将一组数据按大小排序后,排在中间位置的一个数或中间两个数的平均数,那就需要先找到数据按大小排序后,大致排在50%附近的数,再根据中位数的概念进行细化求解.
图2这个扇形图中的数据18~21是按大小顺序旋转排列的,我们就可以像图3所示的这样,先找到最大数据“21”与最小数据“18”的分界半径OM,为找到排在50%附近的数,再作出直径MN,那么射线ON指向的数据就是中位数.
王老师的评价:小明的这个方法是从中位数的概念出发,充分利用了扇形图的特性形象直观地解决问题.
[理解与应用]
请你利用小明的方法直接写出统计表中b的值.
答案解析部分
1.【答案】B
【解析】【解答】解:将这组数据按从小到大进行排序为,
则这组数据的中位数为2,
故答案为:B.
【分析】根据中位数的定义计算求解即可。
2.【答案】D
【解析】【解答】解:由表格可得,
这组数据的众数是11岁,
中位数是11岁.
故选D.
【分析】根据表格中的数据可以得到这组数据的众数和中位数.
3.【答案】D
【解析】【解答】解:将这组数据按从小到大排列为:5,5,5,6, 7,7,10
∵数据5出现3次,次数最多,
∴众数为:5;
∵第四个数为6,
∴中位数为6,
故答案为:D.
【分析】这组数据中出现次数最多的是5,根据众数的概念,即可得出答案;再将这组数据按从小到大排列,这组数据共有7个,故处于最中间位置的是排在第四的位置,根据中位数的定义即可得出答案。
4.【答案】B
【解析】【解答】解:∵ =(156+157+155+156+157+155)÷6=156(cm),
=(158+155+150+154+163+156)÷6=156(cm),
∴ ,
∵S2甲= [2×(156﹣156)2+2×(157﹣156)2+2×(155﹣156)2]= ,
S2乙= [(158﹣156)2+(155﹣156)2+(150﹣156)2+(154﹣156)2+(163﹣156)2+(156﹣156)2]=15 ,
∴S2甲<S2乙,
故答案为:B
【分析】根据平均数和方差的计算公式,逐个计算即可。
5.【答案】D
【解析】【解答】解:∵甲的方差是8.5,乙的方差是60.5,
∴甲的方差小于乙的方差,
∴甲的成绩比乙稳定;
∵甲、乙的平均成绩分别是145,146,
∴平均分相当;
故选:D.
【分析】根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
6.【答案】A
【解析】【解答】解:将数据从小到大排列,则中位数为6,
由于5天出现的次数最多,故众数为5,
故答案为:A
【分析】根据众数和中位数的定义即可求解。
7.【答案】A
【解析】【解答】7个数从小到大排序为:23,25,26,27,30,33,33
位于中间位置的数为27
中位数为27℃,故A符合题意;
出现次数最多的为33
众数是33℃,故B不符合题意;
平均数为℃,故C不符合题意;
观察图象可知,4日至5日最高气温下降幅度较大,故D不符合题意;
故答案为:A.
【分析】根据中位数、众数、平均数的计算和折线统计图的性质逐项判断即可。
8.【答案】C
【解析】解答:
.
所以 .
故选C
分析:考查标准差的计算公式,代入标准差的计算公式即可.
9.【答案】B
【解析】【解答】解:①由条形统计图可得:年用水量不超过180m3的该市居民家庭一共有(0.25+0.75+1.5+1.0+0.5)=4(万),
×100%=80%,故年用水量不超过180m3的该市居民家庭按第一档水价交费,正确;
②∵年用水量超过240m3的该市居民家庭有(0.15+0.15+0.05)=0.35(万),
∴ ×100%=7%≠5%,故年用水量超过240m3的该市居民家庭按第三档水价交费,故此选项错误;
③∵5万个数据的中间是第25000和25001的平均数,
∴该市居民家庭年用水量的中位数在120﹣150之间,故此选项错误;
④由①得,该市居民家庭年用水量的平均数不超过180,正确,
故选:B.
【分析】利用条形统计图结合中位数的定义分别分析得出答案.此题主要考查了频数分布直方图以及中位数的定义,正确利用条形统计图获取正确信息是解题关键.
10.【答案】C
【解析】【解答】当a=1时,有19个数据,最中间是:第10个数据,则中位数是38;
当a=2时,有20个数据,最中间是:第10和11个数据,则中位数是38;
当a=3时,有21个数据,最中间是:第11个数据,则中位数是38;
当a=4时,有22个数据,最中间是:第11和12个数据,则中位数是38;
当a=5时,有23个数据,最中间是:第12个数据,则中位数是38;
当a=6时,有24个数据,最中间是:第12和13个数据,则中位数是38.5;
故该组数据的中位数不大于38,则符合条件的正整数a的取值共有:5个.
故答案为:C.
【分析】根据中位数的定义先排序,由已知中位数不大于38得出处于中位数以上和以下的数据个数应相等,可分类讨论得出结果.
11.【答案】乙
【解析】【解答】∵x丁>x甲>x乙=x丙,
∴从乙和丙中选择一人参加比赛,
∵S 乙2<S 丙2,
∴选择乙参赛,
故答案是:乙.
【分析】根据方差越小,成绩越稳定可知,选乙参赛.
12.【答案】甲
【解析】【解答】解:∵=0.12,=0.6,
∴<,
∴射击成绩较稳定的是甲.
故答案为:甲.
【分析】方差越小,波动越小,据此即可得出答案.
13.【答案】8.5
【解析】【解答】解:由题意得8.5出现的次数最多,
∴张华同学撰实心球成绩的众数是8.5,
故答案为:8.5
【分析】根据众数的定义结合题意即可求解。
14.【答案】120
【解析】【解答】解:y=40a
2-2(a
1+a
2+a
3+…+a
40)a+a
12+a
22+a
3)
2+…+a
402,
因为40>0,
所以当a=
时,y有最小值.
【分析】 利用完全平方公式得到y=40a2-2(a1+a2+a3+…+a40)a+a12+a22+a3)2+…+a402,则可把y看作a的二次函数,然后根据二次函数的性质求解.
15.【答案】4.8或5或5.2
【解析】【解答】解:若a为数据的中位数,则数字排列在数据中第三个位置上。
当a=3时,平均数为
当a=4时,平均数为=5
当a=5时,平均数为=5.2
故答案为:4.8或5或5.2。
【分析】 找数据中的中位数,需要将数据由小到大进行排列,位于中间的数即为中位数,根据a的不同情况进行分类讨论即可。
16.【答案】解:甲的平均成绩为:(87×6+90×4)÷10=88.2(分),
乙的平均成绩为:(91×6+82×4)÷10=87.4(分),
因为甲的平均分数较高,
所以甲将被录取.
【解析】【分析】根据题意先算出甲、乙两位应聘者的加权平均数,再进行比较,即可得出答案.
17.【答案】解:录用张颖,理由如下:张颖的平均成绩是:=89.2(分),李默的平均成绩是:(分),所以录用张颖.
【解析】【分析】根据加权平均数公式,分别求出两人的平均得分即可.
18.【答案】解:(1)平均数:=1(5吨),众数:∵用水量为10吨的最多,∴众数是10吨;中位数:根据第10,11个数据都是15吨,∴中位数是15吨;(2)∵平均数为15吨,∴该社区的月用水量约为:15×500=7500(吨)。
【解析】【分析】此题主要考查了平均数、众数和中位数的定义以及利用样本估计总体,是初中阶段考查重点题型,同学们应重点掌握。
(1)根据图表中数据即可得出20个数据的平均数、众数和中位数;
(2)利用(1)中所求即可得出该社区的月用水量。
19.【答案】(1)7;7.5;4.2
(2)乙;乙;甲
(3)解:乙
【解析】【解答】 (1)如图:环
故第一空填:7
乙的成绩为(环):3,4,6,7,7,8,8,8,9,10,中位数是第五和第六个数据的平均值,
故第二空填:7.5
根据方差公式:
=4.2
故第三空填:4.2
(3)解:选乙更加合适。从中位数和众数的角度来看,乙成绩较好;甲乙平均成绩都是7环,稳定发挥的夺冠可能性较低, 说明乙超水平发挥的概率高,故选乙更加合适。
【分析】 (1) 掌握平均数、中位数、方差的计算方法; (2) 根据中位数和众数进行分析评价; (3)会根据方差判定数据的稳定性和波动性,但不是稳定性越小越好,要根据目标确定。
20.【答案】(1);
(2)-2≤x≤4
(3)解:i)当x>0时, x2 >-2x, 则得-2x最小,即-2x=2, ∴x=-1, 与假设矛盾,不符合。ii)当x≤0时,x2≤-2x, 得x≥-2, 即-2≤x≤0,x2=2, x=-,符合题意 ;x2≥-2x, 得x≤-2, 即-2x=2, x=-1, 与假设矛盾,不符合题意。综上所述,x=-.
(4)解: ∵ M{2,1+x,2x} =i)当即x≥1时,min{2,1+x,2x}=2 ,则x+1=2, x=1, 符合题意。ii)当即x≤1时,min{2,1+x,2x}=2 ,则x+1=2x, ∴x=1, 符合题意。iii)当即x=1时,min{2,1+x,2x}=2, x+1=x+1, 所以x=1符合题意。综上所述, x=1
【解析】【解答】解:(1)
.
(2)∵min(3-2x,1+3x,-5}=-5,∴解得x≤4且x≥-2,∴-2≤x≤4;
【分析】(1)根据条件给出的算法原理计算即可。
(2)根据 min{a,b,c} 算法是要求最小值,列不等式组,求不等式组的解集即可。
(3)根据新定义算法公式,分情况讨论,求出符合条件的x值。
(4)根据新定义算法公式,分别设最小值,求出x, 再验证是否符合条件。
21.【答案】(1)20C组人数为:(人),补全条形统计图如下:
(2)54
(3)86分;87分
(4)1800
【解析】【解答】解:(1)本次调查的学生为:9÷45%=20(名),
故答案为:20;
(2)扇形统计图中,C组所对应的圆心角的度数为:360°x =54°,
故答案为:54;
(3)∵A组分数段内,所有学生得分各不相同,B组学生的成绩分别为:86、86、88、86、83、86,
∴20名学生成绩中,86出现发的次数最多,故本次抽查的学生成绩的众数为86;
∵把20名学生成绩从小到大排列,排在中间的两个数是86,88,
∴中位数为:,
(4)由题意可得:(名),
即估计该校有1800名学生获得优秀,
故答案为:1800.
【分析】(1)根据统计图中的数据计算求解即可;
(2)用360°乘C组占比即可得答案;
(3)根据中位数和众数的定义计算求解即可;
(4)根据题意求出即可作答。
22.【答案】(1)解:
(2)19;19;19,20,21
(3)解:由题意和图3可得,
【解析】【解答】(2)解:由图1可得,众数是19,中位数是19,
由图2可得,19、20、21一样多且数据最大,则众数是19,20,21,
故答案为:19,19;19,20,21
【分析】(1)由图1可以计算出 a 的值;(2)根据图1和图2可以将表格中空格补充完整;(3)根据题意和图3可以直接写出b的值
1 / 1
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
