2023-2024学年浙教版八年级下第四章 平行四边形 单元检测(含解析)
文档属性
| 名称 | 2023-2024学年浙教版八年级下第四章 平行四边形 单元检测(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 607.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-25 00:00:00 | ||
图片预览


文档简介
2023-2024学年八年级下第四章单元检测
综合考试
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 xx 分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、单选题
得分
1.如图,分别是上海、南京、深圳、兰州4个城市的地铁标志,其中是中心对称图形的是( )
A. B. C. D.
2.一个多边形的内角和是它的外角和的6倍,则这个多边形是几边形?( )
A.十一边形 B.十二边形 C.十三边形 D.十四边形
3.小丽利用最近学习的数学知识,给同伴出了这样一道题:如图,小刚从点 A 出发,沿直线走 6米后向左转θ,接着沿直线前进 6 米后,再向左转θ……如此下去,当他第一次回到点A时,发现自己走了 72米,则θ的度数为( )
A.28° B.30° C.33° D.36°
4.如图所示的四边形中,若去掉一个50°的角得到一个五边形,则∠1+∠2等于( )
A.230° B.240° C.250° D.260°
5.过八边形一个顶点的所有对角线,把这个多边形分成三角形的个数是( )
A.5 B.6 C.7 D.8
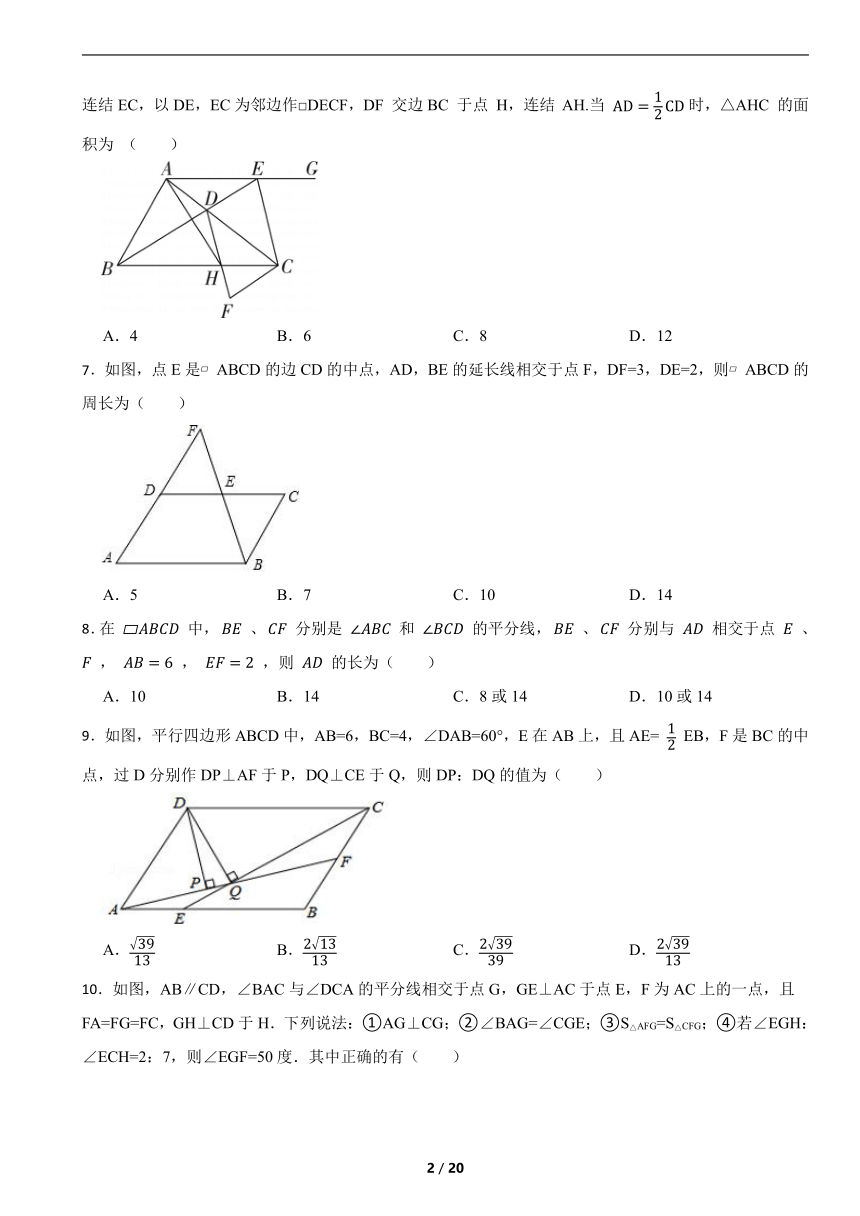
6.如图,△ABC的面积为 24,点D为边AC 上的一点,连结BD 并延长,交 BC 的平行线AG 于点E,连结EC,以DE,EC为邻边作□DECF,DF 交边BC 于点 H,连结 AH.当 时,△AHC 的面积为 ( )
A.4 B.6 C.8 D.12
7.如图,点E是 ABCD的边CD的中点,AD,BE的延长线相交于点F,DF=3,DE=2,则 ABCD的周长为( )
A.5 B.7 C.10 D.14
8.在 中, 、 分别是 和 的平分线, 、 分别与 相交于点 、 , , ,则 的长为( )
A.10 B.14 C.8或14 D.10或14
9.如图,平行四边形ABCD中,AB=6,BC=4,∠DAB=60°,E在AB上,且AE= EB,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ的值为( )
A. B. C. D.
10.如图,AB∥CD,∠BAC与∠DCA的平分线相交于点G,GE⊥AC于点E,F为AC上的一点,且FA=FG=FC,GH⊥CD于H.下列说法:①AG⊥CG;②∠BAG=∠CGE;③S△AFG=S△CFG;④若∠EGH:∠ECH=2:7,则∠EGF=50度.其中正确的有( )
A.①②③④ B.②③④ C.①③④ D.①②④
阅卷人 二、填空题
得分
11.若一个多边形的内角和为1800°,则这个多边形 边形.
12.如图,在 中, , 是 的角平分线,E是 中点,连接 ,若 ,则 .
13.已知如图所示,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,则当△PAB的周长取最小值时,∠APB的度数为 °.
14.如图,已知三角形ABC的面积为12,将三角形ABC沿BC平移到三角形A′B′C′,使B′与C重合,A C′交A′C ′与点D,点D是A ′C的中点,则三角形C ′DC的面积为 。
15.如图,在平面直角坐标系中,点A,B,C的坐标分别为,,.点M从坐标原点O出发,第一次跳跃到点,使得点与点O关于点A成中心对称;第二次跳跃到点,使得点与点关于点B成中心对称;第三次跳跃到点,使得点与点关于点C成中心对称;第四次跳跃到点,使得点与点关于点A成中心对称;…,依此方式跳跃,点的坐标是 .
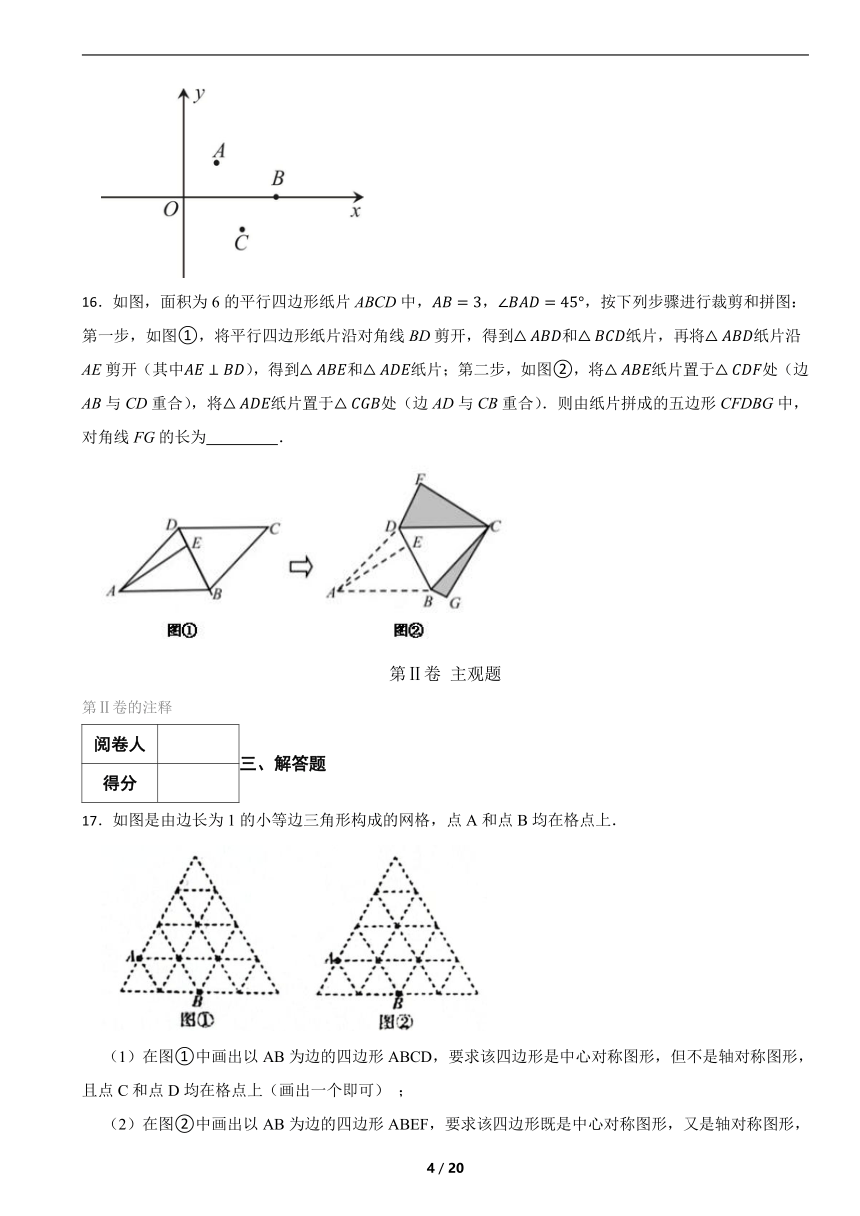
16.如图,面积为6的平行四边形纸片ABCD中,,,按下列步骤进行裁剪和拼图:第一步,如图①,将平行四边形纸片沿对角线BD剪开,得到和纸片,再将纸片沿AE剪开(其中),得到和纸片;第二步,如图②,将纸片置于处(边AB与CD重合),将纸片置于处(边AD与CB重合).则由纸片拼成的五边形CFDBG中,对角线FG的长为 .
第Ⅱ卷 主观题
第Ⅱ卷的注释
阅卷人 三、解答题
得分
17.如图是由边长为1的小等边三角形构成的网格,点A和点B均在格点上.
(1)在图①中画出以AB为边的四边形ABCD,要求该四边形是中心对称图形,但不是轴对称图形,且点C和点D均在格点上(画出一个即可) ;
(2)在图②中画出以AB为边的四边形ABEF,要求该四边形既是中心对称图形,又是轴对称图形,且点E和点F均在格点上(画出一个即可).
18.已知一个n边形的每一个内角都等于150°.
(1)求n.
(2)求这个n边形的内角和.
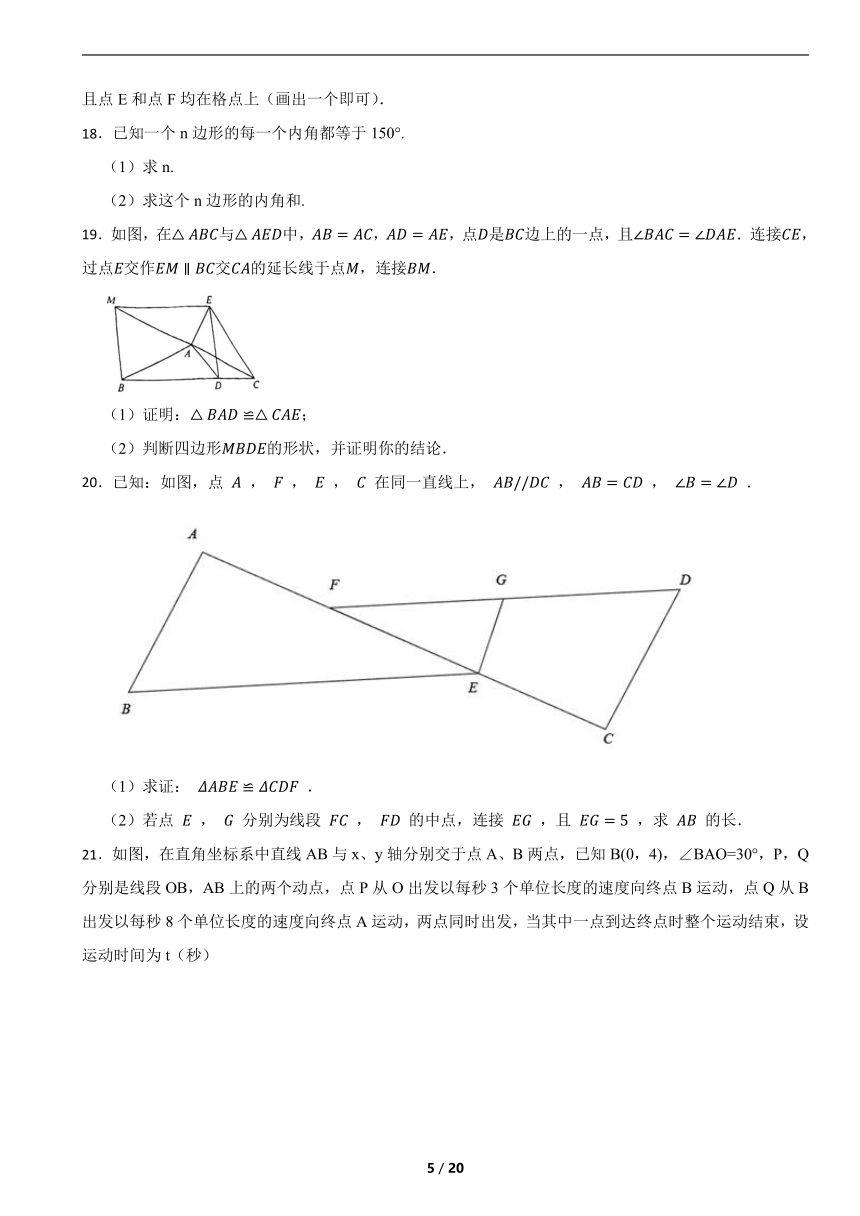
19.如图,在与中,,,点是边上的一点,且.连接,过点交作交的延长线于点,连接.
(1)证明:;
(2)判断四边形的形状,并证明你的结论.
20.已知:如图,点 , , , 在同一直线上, , , .
(1)求证: .
(2)若点 , 分别为线段 , 的中点,连接 ,且 ,求 的长.
21.如图,在直角坐标系中直线AB与x、y轴分别交于点A、B两点,已知B(0,4),∠BAO=30°,P,Q分别是线段OB,AB上的两个动点,点P从O出发以每秒3个单位长度的速度向终点B运动,点Q从B出发以每秒8个单位长度的速度向终点A运动,两点同时出发,当其中一点到达终点时整个运动结束,设运动时间为t(秒)
(1)求点A的坐标和线段AB的长;
(2)当t为何值时,△BPQ的面积为2 ;
(3)若C为OA的中点,连结QC,QP,以QC,QP为邻边作平行四边形PQCD,
①t为何值时,点D恰好落在坐标轴上;
②是否存在这样的 ,使x轴将平行四边形PQCD的面积分成1:3的两部分,若存在,请直接写出 的值。
22.探究题
(1)【证法回顾】
证明:三角形中位线定理.
已知:如图1,DE是△ABC的中位线.
求证:DE∥BC,DE= BC.
证明:添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;请继续完成证明过程:
(2)【问题解决】
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)【拓展研究】如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=3 ,DF=2,∠GEF=90°,求GF的长.
答案解析部分
1.【答案】C
【解析】【解答】A、是轴对称图形,不是中心对称图形,故不符合题意;
B、是轴对称图形,不是中心对称图形,故不符合题意;
C、既是轴对称图形,也是中心对称图形,故符合题意;
D、既不是轴对称图形,也不是中心对称图形,故不符合题意。
故答案为:C。
【分析】把一个平面图形,沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形;把一个平面图形,沿着某一点旋转180°后,能与自身重合的图形就是中心对称图形,根据定义即可一一判断得出答案。
2.【答案】D
【解析】【解答】解:设这个多边形的边数是n,
则(n-2)×180°=6×360°,
解得:n=14,
即这个多边形是十四边形;
故答案为:D.
【分析】设这个多边形的边数是n,根据多边形内角和定理:(n-2)·180° 与多边形的外角和等于360°列方程,求解即可得出答案.
3.【答案】B
【解析】【解答】解:∵小丽第一次回到点A时,所经过的路线刚好构成一个正多边形,
∴多边形的边数=72÷6=12,
∵多边形的外角和=360°,
∴小丽每次转过的角度θ=360°÷12=30°.
故答案为:B.
【分析】根据小丽第一次回到点A时,所经过的路线刚好构成一个正多边形,可求出这个多边形的边数,然后根据多边形的外角和等于360度可求解.
4.【答案】A
【解析】【解答】如图,
在四边形ABCD中,∠A+∠B+∠C+∠D=360°,
∴∠B+∠C+∠D=360° ∠A,
在五边形中,∠1+∠2+∠B+∠C+∠D=(5 2)×180°=540°
∴∠1+∠2=540° (∠B+∠C+∠D)=540° (360° ∠A)=540° 360°+∠A=180°+50°=230°.
故答案为:A.
【分析】根据多边形内角和定理,分别求出四边形、五边形内角和,分析即可求得 ∠1+∠2 。
5.【答案】B
【解析】【解答】解:∵过八边形一个顶点的对角线有5条对角线,它们把八边形分为了6个三角形,
∴分成的三角形个数是8.
故答案为:B.
【分析】根据过n边形一个顶点出发的对角线分得的三角形个数=n-2,可得:过八边形一个顶点的所有对角线,把这个多边形分成6个三角形.
6.【答案】C
【解析】【解答】解:如图,连接,
的面积为,,
,
,
,,
,
四边形是平行四边形,
,
,
故答案为:C.
【分析】本题考查平行四边形的性质,三角形的面积公式.先连接,根据的面积为,,可推出;又知,可推出,
由面积的和差关系可求得,再结合可得出答案.
7.【答案】D
【解析】【解答】解:∵四边形ABCD为平行四边形,
∴DC AB,AD BC,
∵E为CD的中点,
∴DE为△FAB的中位线,
∴AD=DF,DE= AB,
∵DF=3,DE=2,
∴AD=3,AB=4,
∴四边形ABCD的周长为:2(AD+AB)=14.
故选D.
【分析】根据平行四边形的性质可知DC AB,然后根据E为CD的中点可证DE为△FAB的中位线,已知DF=3,DE=2,可求得AD,AB的长度,继而可求得ABCD的周长.
8.【答案】D
【解析】【解答】分两种情况进行讨论
如图1:
在 中,AB=CD,AD//BC
∴
又∵BE平分
∴
∴
∴AB=AE=6
同理可得:DF=DC=6
∵EF=2
∴AD=AE+DF-EF=10
如图2:
在 中,AB=CD,AD//BC
∴
又∵BE平分
∴
∴
∴AB=AE=6
同理可得:DF=DC=6
∵EF=2
∴AD=AE+DF+EF=14
综上所述:AD的值为10或14
故答案为:D.
【分析】当BE与CF相交时,由平行四边形的性质以及平行线的性质可得∠AEB=∠EBC,由角平分线的概念可得∠ABE=∠EBC,进而可得到AB=AE=6,同理可得:DF=DC=6,据此求解,同理可求出当BE与CF不相交时,AD的值.
9.【答案】D
【解析】【解答】解:连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,如图所示,
由题意得:
,,
∴,
∴,
,
∵四边形ABCD是平行四边形,
∴AD//BC,
∵∠DAB = 60° ,
∴∠CBN =∠DAB= 60° ,
∴∠BFN=∠MCB=30°,
又∵BC=4,AE:EB=1:2,AB=6,F是BC的中点,
∴BF=2,BN=1,BE=4,BM=2,
由勾股定理得:
,,
,
,
∴,
∴=,
故答案为:D.
【分析】连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,根据三角形的面积和平行四边形的面积以及"同底等高"可知,,得出,再根据勾股定理得出AF、CE的值,代入求比即可.
10.【答案】A
【解析】【分析】灵活利用平行线的性质、等角的余角相等、四边形的内角和、等边对等角、三角形的面积公式、角平分线的性质进行分析。
【解答】①中,根据两条直线平行,同旁内角互补,得∠BAC+∠ACD=180°,
再根据角平分线的概念,得∠GAC+∠GCA=∠BAC+∠ACD=×180°=90°,
再根据三角形的内角和是180°,得AG⊥CG;
②中,根据等角的余角相等,得∠CGE=∠GAC,故∠BAG=∠CGE;
③中,根据三角形的面积公式,
∵AF=CF,∴S△AFG=S△CFG;
④中,根据题意,得:在四边形GECH中,∠EGH+∠ECH=180°.
又∠EGH:∠ECH=2:7,则∠EGH=180°×=40°,∠ECH=180°×=140°.
∵CG平分∠ECH,∴∠FCG=∠ECH=70°,
根据直角三角形的两个锐角互余,得∠EGC=20°.
∵FG=FC,
∴∠FGC=∠FCG=70°,
∴∠EGF=50°.
故上述四个都是正确的。
【点评】此题的综合性较强,运用了平行线的性质、等角的余角相等、四边形的内角和公式、等边对等角、三角形的面积公式、角平分线的概念。
11.【答案】十二
【解析】【解答】解:设这个多边形的边数是n,
则,
解得:.
故答案为:十二.
【分析】根据多边形的内角和公式(n-2)×180°进行计算.
12.【答案】6
【解析】【解答】解:∵AB=AC,AD平分∠BAC,
∴D为BC的中点,
∵E为AC的中点,
∴AB=2DE=6.
故答案为:6.
【分析】利用等腰三角形三线合一的性质可证得D为BC的中点,再由点E是AC的中点,可证得DE是△ABC的中位线,利用三角形的中位线定理,可求出AB的长.
13.【答案】100
【解析】【解答】如图,作出P点关于OM、ON的对称点P1,P2连接P1,P2交OM,ON于A、B两点,此时△PAB的周长最小,由题意可知∠P1PP2=180°-∠MON=180°-40°=140°,
∴∠P1PA+∠P2PB=∠P1+∠P2=180°-∠P1PP2=40°,
∴∠APB=140°-40°=100°.
故答案为:100°.
【分析】作出P点关于OM、ON的对称点P1,P2连接P1,P2交OM,ON于A、B两点,此时△PAB的周长最小,再由四边形内和定理即可求出答案.
14.【答案】6
【解析】【解答】解:根据题意得,∠B=∠A′CC′,BC=B′C′,
∴CD∥AB,
∴CD=AB,
∵点C′到A′C的距离等于点C到AB的距离,
∴△C′DC的面积=△ABC的面积=12×12=6.
故答案为:6.
【分析】 根据平移的性质得出∠B=∠A′CC′,BC=B′C′,再根据同位角相等,两直线平行得CD∥AB,根据三角形中位线定理得出CD=AB,再根据点C′到A′C的距离等于点C到AB的距离,得出△C′DC的面积=△ABC的面积,即可得出答案.
15.【答案】
【解析】【解答】解:∵点M从坐标原点O出发,第一次跳跃到点M1,点M1与点O关于点A成中心对称,点的坐标为(1,1),
点的坐标为(2,2),
点与点M1关于点B成中心对称,点的坐标为(3,0),
点的坐标为(4,-2),
点与点M2关于点C成中心对称,点C的坐标为(2,-1),
点的坐标为(0,0),
点又回到了原点,
∴按照此规律跳跃,每三个点循环一次,
,
∴点正好在原点,
∴点的坐标为(0,0).
故答案为:(0,0).
【分析】根据中心对称的性质分别求出M1、M2、M3的坐标,可知按照此规律跳跃,每三个点循环一次,由于,可知点M2022刚好和M3的坐标一致,即得结论;
16.【答案】
17.【答案】(1)解:如图①所示,四边形ABCD即为所求.
(2)解:如图②所示,四边形ABEF即为所求.
【解析】【分析】(1)根据中心对称图形、轴对称图形的含义作图即可;
(2)同理,根据中心对称图形、轴对称图形的含义作图。
18.【答案】(1)解:∵每一个内角都等于150°,
∴每一个外角都等于180°-150°=30°,
∴边数n=360°÷30°=12;
(2)解:内角和:12×150°=1800°.
【解析】【分析】(1)首先求出外角度数,再用360°除以外角度数可得答案;(2)利用每一个内角度数150°×内角的个数即可.
19.【答案】(1)证明:∵.即∠BAD+∠CAD=∠CAE+∠CAD,
∴∠BAD=∠CAE,
∵,,
∴;
(2)解:四边形MBDE为平行四边形,证明如下:
∵,
∴BD=CE,∠ABD=∠ACE,
∵AB=AC,
∴∠ABD=∠ACB,
∴∠ACE =∠ACB,
∵ME∥BC,
∴∠AC B =∠EMC,
∴∠EMC=∠ACE,
∴ME=CE,
∴BD=ME,
又∵BD∥ME,
∴四边形MBDE为平行四边形.
【解析】【分析】(1) 由,可推出∠BAD=∠CAE,根据SAS证明;
(2) 四边形MBDE为平行四边形,证明:由可得BD=CE,∠ABD=∠ACE,再根据等腰三角形的性质及平行线的性质可推出BD=ME,由BD∥ME,根据平行四边形的判定即证.
20.【答案】(1)证明:∵ ,
∴ ,
在 与 中 ,
∴
(2)解:∵点 , 分别为线段 , 的中点,
∴ ,
∵ ,
∴ ,
∵ ,
∴
【解析】【分析】(1) 利用三角形全等即可;
(2)由点 , 分别为线段 , 的中点,得出,由,得出 的长.
21.【答案】(1)解:∵∠BAO=30°,OB=4,
∴AB=2OB=8,
∴OA=ABcos30°=8×=4,
∴A(4,0).
(2)解:作 QH⊥OB 于H,
∵BQ=8t
∴
OP=3t,BP=4-3t
∴
∴
(3)①当 D 在 y 轴上时,QC∥BD,
得 BQ=8t=4,
当 D 在 x 轴上时,PQ∥AD
得 0.5BQ+OP=4
4t+3t=4,
②
若 x 轴恰好将平行四边形 PQCD 的面积分成 1∶3 的两部分,则 E 为 PD 的中点,
∴DF=OP=3t
可以证得 DF=HP
∴3t+3t+4t=4,
【解析】【分析】(1)根据B点坐标得出OB的长,再用含30度角的直角三角形的性质求出OA,即可解答;
(2) 作 QH⊥OB 于H, 分别把BQ和BP用含t的代数式表示,结合含30度角的直角三角形的性质把HQ表示出来,然后根据△BPQ的面积为2 建立方程求解,即可解答;
(3)①分两种情况讨论, 当D在y轴上时,QC∥BD,当D在x轴上时,PQ∥AD,分别利用平行四边形的性质建立方程,即可解答;②根据这个三角形和平行四边形等高的特点先确定出点E是DP中点,则可得出DF= OP,再利用三角形全等求出DF= PH,据此列方程求解即可.
22.【答案】(1)证明:如图,延长DE 到点F,使得EF=DE,连接CF
在△ADE和△CFE中, ,
∴△ADE≌△CFE(SAS),
∴∠A=∠ECF,AD=CF,
∴CF∥AB,
又∵AD=BD,
∴CF=BD,
∴四边形BCFD是平行四边形,
∴DE∥BC,DE= BC.
故答案为:DE∥BC,DE= BC
(2)如图2,延长GE、FD交于点H,
∵E为AD中点,
∴EA=ED,且∠A=∠EDH=90°,
在△AEG和△DEH中,
∴△AEG≌△DEH(ASA),
∴AG=HD=2,EG=EH,
∵∠GEF=90°,
∴EF垂直平分GH,
∴GF=HF=DH+DF=2+3=5;
(3)如图3,过点D作AB的平行线交GE的延长线于点H,过H作CD的垂线,垂足为P,连接HF,
同(1)可知△AEG≌△DEH,GF=HF,
∴∠A=∠HDE=105°,AG=HD= ,
∵∠ADC=120°,
∴∠HDF=360°﹣105°﹣120°=135°,
∴∠HDP=45°,
∴△PDH为等腰直角三角形,
∴PD=PH=3,
∴PF=PD+DF=3+2=5,
在Rt△HFP中,∠HPF=90°,HP=3,PF=5,
∴HF= ═
∴GF= .
【解析】【分析】(1)利用“边角边”证明△ADE和△CEF全等,根据全等三角形对应边相等可得AD=CF,然后判断出四边形BCFD是平行四边形,根据平行四边形的性质可得;(2)先判断出△AEG≌△DEH(ASA)进而判断出EF垂直平分GH,即可得出结论;(3)先求出AG=HD= ,进而判断出△PDH为等腰直角三角形,再用勾股定理求出HF即可得出结论.
1 / 1
综合考试
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 xx 分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、单选题
得分
1.如图,分别是上海、南京、深圳、兰州4个城市的地铁标志,其中是中心对称图形的是( )
A. B. C. D.
2.一个多边形的内角和是它的外角和的6倍,则这个多边形是几边形?( )
A.十一边形 B.十二边形 C.十三边形 D.十四边形
3.小丽利用最近学习的数学知识,给同伴出了这样一道题:如图,小刚从点 A 出发,沿直线走 6米后向左转θ,接着沿直线前进 6 米后,再向左转θ……如此下去,当他第一次回到点A时,发现自己走了 72米,则θ的度数为( )
A.28° B.30° C.33° D.36°
4.如图所示的四边形中,若去掉一个50°的角得到一个五边形,则∠1+∠2等于( )
A.230° B.240° C.250° D.260°
5.过八边形一个顶点的所有对角线,把这个多边形分成三角形的个数是( )
A.5 B.6 C.7 D.8
6.如图,△ABC的面积为 24,点D为边AC 上的一点,连结BD 并延长,交 BC 的平行线AG 于点E,连结EC,以DE,EC为邻边作□DECF,DF 交边BC 于点 H,连结 AH.当 时,△AHC 的面积为 ( )
A.4 B.6 C.8 D.12
7.如图,点E是 ABCD的边CD的中点,AD,BE的延长线相交于点F,DF=3,DE=2,则 ABCD的周长为( )
A.5 B.7 C.10 D.14
8.在 中, 、 分别是 和 的平分线, 、 分别与 相交于点 、 , , ,则 的长为( )
A.10 B.14 C.8或14 D.10或14
9.如图,平行四边形ABCD中,AB=6,BC=4,∠DAB=60°,E在AB上,且AE= EB,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ的值为( )
A. B. C. D.
10.如图,AB∥CD,∠BAC与∠DCA的平分线相交于点G,GE⊥AC于点E,F为AC上的一点,且FA=FG=FC,GH⊥CD于H.下列说法:①AG⊥CG;②∠BAG=∠CGE;③S△AFG=S△CFG;④若∠EGH:∠ECH=2:7,则∠EGF=50度.其中正确的有( )
A.①②③④ B.②③④ C.①③④ D.①②④
阅卷人 二、填空题
得分
11.若一个多边形的内角和为1800°,则这个多边形 边形.
12.如图,在 中, , 是 的角平分线,E是 中点,连接 ,若 ,则 .
13.已知如图所示,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,则当△PAB的周长取最小值时,∠APB的度数为 °.
14.如图,已知三角形ABC的面积为12,将三角形ABC沿BC平移到三角形A′B′C′,使B′与C重合,A C′交A′C ′与点D,点D是A ′C的中点,则三角形C ′DC的面积为 。
15.如图,在平面直角坐标系中,点A,B,C的坐标分别为,,.点M从坐标原点O出发,第一次跳跃到点,使得点与点O关于点A成中心对称;第二次跳跃到点,使得点与点关于点B成中心对称;第三次跳跃到点,使得点与点关于点C成中心对称;第四次跳跃到点,使得点与点关于点A成中心对称;…,依此方式跳跃,点的坐标是 .
16.如图,面积为6的平行四边形纸片ABCD中,,,按下列步骤进行裁剪和拼图:第一步,如图①,将平行四边形纸片沿对角线BD剪开,得到和纸片,再将纸片沿AE剪开(其中),得到和纸片;第二步,如图②,将纸片置于处(边AB与CD重合),将纸片置于处(边AD与CB重合).则由纸片拼成的五边形CFDBG中,对角线FG的长为 .
第Ⅱ卷 主观题
第Ⅱ卷的注释
阅卷人 三、解答题
得分
17.如图是由边长为1的小等边三角形构成的网格,点A和点B均在格点上.
(1)在图①中画出以AB为边的四边形ABCD,要求该四边形是中心对称图形,但不是轴对称图形,且点C和点D均在格点上(画出一个即可) ;
(2)在图②中画出以AB为边的四边形ABEF,要求该四边形既是中心对称图形,又是轴对称图形,且点E和点F均在格点上(画出一个即可).
18.已知一个n边形的每一个内角都等于150°.
(1)求n.
(2)求这个n边形的内角和.
19.如图,在与中,,,点是边上的一点,且.连接,过点交作交的延长线于点,连接.
(1)证明:;
(2)判断四边形的形状,并证明你的结论.
20.已知:如图,点 , , , 在同一直线上, , , .
(1)求证: .
(2)若点 , 分别为线段 , 的中点,连接 ,且 ,求 的长.
21.如图,在直角坐标系中直线AB与x、y轴分别交于点A、B两点,已知B(0,4),∠BAO=30°,P,Q分别是线段OB,AB上的两个动点,点P从O出发以每秒3个单位长度的速度向终点B运动,点Q从B出发以每秒8个单位长度的速度向终点A运动,两点同时出发,当其中一点到达终点时整个运动结束,设运动时间为t(秒)
(1)求点A的坐标和线段AB的长;
(2)当t为何值时,△BPQ的面积为2 ;
(3)若C为OA的中点,连结QC,QP,以QC,QP为邻边作平行四边形PQCD,
①t为何值时,点D恰好落在坐标轴上;
②是否存在这样的 ,使x轴将平行四边形PQCD的面积分成1:3的两部分,若存在,请直接写出 的值。
22.探究题
(1)【证法回顾】
证明:三角形中位线定理.
已知:如图1,DE是△ABC的中位线.
求证:DE∥BC,DE= BC.
证明:添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;请继续完成证明过程:
(2)【问题解决】
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)【拓展研究】如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=3 ,DF=2,∠GEF=90°,求GF的长.
答案解析部分
1.【答案】C
【解析】【解答】A、是轴对称图形,不是中心对称图形,故不符合题意;
B、是轴对称图形,不是中心对称图形,故不符合题意;
C、既是轴对称图形,也是中心对称图形,故符合题意;
D、既不是轴对称图形,也不是中心对称图形,故不符合题意。
故答案为:C。
【分析】把一个平面图形,沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形;把一个平面图形,沿着某一点旋转180°后,能与自身重合的图形就是中心对称图形,根据定义即可一一判断得出答案。
2.【答案】D
【解析】【解答】解:设这个多边形的边数是n,
则(n-2)×180°=6×360°,
解得:n=14,
即这个多边形是十四边形;
故答案为:D.
【分析】设这个多边形的边数是n,根据多边形内角和定理:(n-2)·180° 与多边形的外角和等于360°列方程,求解即可得出答案.
3.【答案】B
【解析】【解答】解:∵小丽第一次回到点A时,所经过的路线刚好构成一个正多边形,
∴多边形的边数=72÷6=12,
∵多边形的外角和=360°,
∴小丽每次转过的角度θ=360°÷12=30°.
故答案为:B.
【分析】根据小丽第一次回到点A时,所经过的路线刚好构成一个正多边形,可求出这个多边形的边数,然后根据多边形的外角和等于360度可求解.
4.【答案】A
【解析】【解答】如图,
在四边形ABCD中,∠A+∠B+∠C+∠D=360°,
∴∠B+∠C+∠D=360° ∠A,
在五边形中,∠1+∠2+∠B+∠C+∠D=(5 2)×180°=540°
∴∠1+∠2=540° (∠B+∠C+∠D)=540° (360° ∠A)=540° 360°+∠A=180°+50°=230°.
故答案为:A.
【分析】根据多边形内角和定理,分别求出四边形、五边形内角和,分析即可求得 ∠1+∠2 。
5.【答案】B
【解析】【解答】解:∵过八边形一个顶点的对角线有5条对角线,它们把八边形分为了6个三角形,
∴分成的三角形个数是8.
故答案为:B.
【分析】根据过n边形一个顶点出发的对角线分得的三角形个数=n-2,可得:过八边形一个顶点的所有对角线,把这个多边形分成6个三角形.
6.【答案】C
【解析】【解答】解:如图,连接,
的面积为,,
,
,
,,
,
四边形是平行四边形,
,
,
故答案为:C.
【分析】本题考查平行四边形的性质,三角形的面积公式.先连接,根据的面积为,,可推出;又知,可推出,
由面积的和差关系可求得,再结合可得出答案.
7.【答案】D
【解析】【解答】解:∵四边形ABCD为平行四边形,
∴DC AB,AD BC,
∵E为CD的中点,
∴DE为△FAB的中位线,
∴AD=DF,DE= AB,
∵DF=3,DE=2,
∴AD=3,AB=4,
∴四边形ABCD的周长为:2(AD+AB)=14.
故选D.
【分析】根据平行四边形的性质可知DC AB,然后根据E为CD的中点可证DE为△FAB的中位线,已知DF=3,DE=2,可求得AD,AB的长度,继而可求得ABCD的周长.
8.【答案】D
【解析】【解答】分两种情况进行讨论
如图1:
在 中,AB=CD,AD//BC
∴
又∵BE平分
∴
∴
∴AB=AE=6
同理可得:DF=DC=6
∵EF=2
∴AD=AE+DF-EF=10
如图2:
在 中,AB=CD,AD//BC
∴
又∵BE平分
∴
∴
∴AB=AE=6
同理可得:DF=DC=6
∵EF=2
∴AD=AE+DF+EF=14
综上所述:AD的值为10或14
故答案为:D.
【分析】当BE与CF相交时,由平行四边形的性质以及平行线的性质可得∠AEB=∠EBC,由角平分线的概念可得∠ABE=∠EBC,进而可得到AB=AE=6,同理可得:DF=DC=6,据此求解,同理可求出当BE与CF不相交时,AD的值.
9.【答案】D
【解析】【解答】解:连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,如图所示,
由题意得:
,,
∴,
∴,
,
∵四边形ABCD是平行四边形,
∴AD//BC,
∵∠DAB = 60° ,
∴∠CBN =∠DAB= 60° ,
∴∠BFN=∠MCB=30°,
又∵BC=4,AE:EB=1:2,AB=6,F是BC的中点,
∴BF=2,BN=1,BE=4,BM=2,
由勾股定理得:
,,
,
,
∴,
∴=,
故答案为:D.
【分析】连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,根据三角形的面积和平行四边形的面积以及"同底等高"可知,,得出,再根据勾股定理得出AF、CE的值,代入求比即可.
10.【答案】A
【解析】【分析】灵活利用平行线的性质、等角的余角相等、四边形的内角和、等边对等角、三角形的面积公式、角平分线的性质进行分析。
【解答】①中,根据两条直线平行,同旁内角互补,得∠BAC+∠ACD=180°,
再根据角平分线的概念,得∠GAC+∠GCA=∠BAC+∠ACD=×180°=90°,
再根据三角形的内角和是180°,得AG⊥CG;
②中,根据等角的余角相等,得∠CGE=∠GAC,故∠BAG=∠CGE;
③中,根据三角形的面积公式,
∵AF=CF,∴S△AFG=S△CFG;
④中,根据题意,得:在四边形GECH中,∠EGH+∠ECH=180°.
又∠EGH:∠ECH=2:7,则∠EGH=180°×=40°,∠ECH=180°×=140°.
∵CG平分∠ECH,∴∠FCG=∠ECH=70°,
根据直角三角形的两个锐角互余,得∠EGC=20°.
∵FG=FC,
∴∠FGC=∠FCG=70°,
∴∠EGF=50°.
故上述四个都是正确的。
【点评】此题的综合性较强,运用了平行线的性质、等角的余角相等、四边形的内角和公式、等边对等角、三角形的面积公式、角平分线的概念。
11.【答案】十二
【解析】【解答】解:设这个多边形的边数是n,
则,
解得:.
故答案为:十二.
【分析】根据多边形的内角和公式(n-2)×180°进行计算.
12.【答案】6
【解析】【解答】解:∵AB=AC,AD平分∠BAC,
∴D为BC的中点,
∵E为AC的中点,
∴AB=2DE=6.
故答案为:6.
【分析】利用等腰三角形三线合一的性质可证得D为BC的中点,再由点E是AC的中点,可证得DE是△ABC的中位线,利用三角形的中位线定理,可求出AB的长.
13.【答案】100
【解析】【解答】如图,作出P点关于OM、ON的对称点P1,P2连接P1,P2交OM,ON于A、B两点,此时△PAB的周长最小,由题意可知∠P1PP2=180°-∠MON=180°-40°=140°,
∴∠P1PA+∠P2PB=∠P1+∠P2=180°-∠P1PP2=40°,
∴∠APB=140°-40°=100°.
故答案为:100°.
【分析】作出P点关于OM、ON的对称点P1,P2连接P1,P2交OM,ON于A、B两点,此时△PAB的周长最小,再由四边形内和定理即可求出答案.
14.【答案】6
【解析】【解答】解:根据题意得,∠B=∠A′CC′,BC=B′C′,
∴CD∥AB,
∴CD=AB,
∵点C′到A′C的距离等于点C到AB的距离,
∴△C′DC的面积=△ABC的面积=12×12=6.
故答案为:6.
【分析】 根据平移的性质得出∠B=∠A′CC′,BC=B′C′,再根据同位角相等,两直线平行得CD∥AB,根据三角形中位线定理得出CD=AB,再根据点C′到A′C的距离等于点C到AB的距离,得出△C′DC的面积=△ABC的面积,即可得出答案.
15.【答案】
【解析】【解答】解:∵点M从坐标原点O出发,第一次跳跃到点M1,点M1与点O关于点A成中心对称,点的坐标为(1,1),
点的坐标为(2,2),
点与点M1关于点B成中心对称,点的坐标为(3,0),
点的坐标为(4,-2),
点与点M2关于点C成中心对称,点C的坐标为(2,-1),
点的坐标为(0,0),
点又回到了原点,
∴按照此规律跳跃,每三个点循环一次,
,
∴点正好在原点,
∴点的坐标为(0,0).
故答案为:(0,0).
【分析】根据中心对称的性质分别求出M1、M2、M3的坐标,可知按照此规律跳跃,每三个点循环一次,由于,可知点M2022刚好和M3的坐标一致,即得结论;
16.【答案】
17.【答案】(1)解:如图①所示,四边形ABCD即为所求.
(2)解:如图②所示,四边形ABEF即为所求.
【解析】【分析】(1)根据中心对称图形、轴对称图形的含义作图即可;
(2)同理,根据中心对称图形、轴对称图形的含义作图。
18.【答案】(1)解:∵每一个内角都等于150°,
∴每一个外角都等于180°-150°=30°,
∴边数n=360°÷30°=12;
(2)解:内角和:12×150°=1800°.
【解析】【分析】(1)首先求出外角度数,再用360°除以外角度数可得答案;(2)利用每一个内角度数150°×内角的个数即可.
19.【答案】(1)证明:∵.即∠BAD+∠CAD=∠CAE+∠CAD,
∴∠BAD=∠CAE,
∵,,
∴;
(2)解:四边形MBDE为平行四边形,证明如下:
∵,
∴BD=CE,∠ABD=∠ACE,
∵AB=AC,
∴∠ABD=∠ACB,
∴∠ACE =∠ACB,
∵ME∥BC,
∴∠AC B =∠EMC,
∴∠EMC=∠ACE,
∴ME=CE,
∴BD=ME,
又∵BD∥ME,
∴四边形MBDE为平行四边形.
【解析】【分析】(1) 由,可推出∠BAD=∠CAE,根据SAS证明;
(2) 四边形MBDE为平行四边形,证明:由可得BD=CE,∠ABD=∠ACE,再根据等腰三角形的性质及平行线的性质可推出BD=ME,由BD∥ME,根据平行四边形的判定即证.
20.【答案】(1)证明:∵ ,
∴ ,
在 与 中 ,
∴
(2)解:∵点 , 分别为线段 , 的中点,
∴ ,
∵ ,
∴ ,
∵ ,
∴
【解析】【分析】(1) 利用三角形全等即可;
(2)由点 , 分别为线段 , 的中点,得出,由,得出 的长.
21.【答案】(1)解:∵∠BAO=30°,OB=4,
∴AB=2OB=8,
∴OA=ABcos30°=8×=4,
∴A(4,0).
(2)解:作 QH⊥OB 于H,
∵BQ=8t
∴
OP=3t,BP=4-3t
∴
∴
(3)①当 D 在 y 轴上时,QC∥BD,
得 BQ=8t=4,
当 D 在 x 轴上时,PQ∥AD
得 0.5BQ+OP=4
4t+3t=4,
②
若 x 轴恰好将平行四边形 PQCD 的面积分成 1∶3 的两部分,则 E 为 PD 的中点,
∴DF=OP=3t
可以证得 DF=HP
∴3t+3t+4t=4,
【解析】【分析】(1)根据B点坐标得出OB的长,再用含30度角的直角三角形的性质求出OA,即可解答;
(2) 作 QH⊥OB 于H, 分别把BQ和BP用含t的代数式表示,结合含30度角的直角三角形的性质把HQ表示出来,然后根据△BPQ的面积为2 建立方程求解,即可解答;
(3)①分两种情况讨论, 当D在y轴上时,QC∥BD,当D在x轴上时,PQ∥AD,分别利用平行四边形的性质建立方程,即可解答;②根据这个三角形和平行四边形等高的特点先确定出点E是DP中点,则可得出DF= OP,再利用三角形全等求出DF= PH,据此列方程求解即可.
22.【答案】(1)证明:如图,延长DE 到点F,使得EF=DE,连接CF
在△ADE和△CFE中, ,
∴△ADE≌△CFE(SAS),
∴∠A=∠ECF,AD=CF,
∴CF∥AB,
又∵AD=BD,
∴CF=BD,
∴四边形BCFD是平行四边形,
∴DE∥BC,DE= BC.
故答案为:DE∥BC,DE= BC
(2)如图2,延长GE、FD交于点H,
∵E为AD中点,
∴EA=ED,且∠A=∠EDH=90°,
在△AEG和△DEH中,
∴△AEG≌△DEH(ASA),
∴AG=HD=2,EG=EH,
∵∠GEF=90°,
∴EF垂直平分GH,
∴GF=HF=DH+DF=2+3=5;
(3)如图3,过点D作AB的平行线交GE的延长线于点H,过H作CD的垂线,垂足为P,连接HF,
同(1)可知△AEG≌△DEH,GF=HF,
∴∠A=∠HDE=105°,AG=HD= ,
∵∠ADC=120°,
∴∠HDF=360°﹣105°﹣120°=135°,
∴∠HDP=45°,
∴△PDH为等腰直角三角形,
∴PD=PH=3,
∴PF=PD+DF=3+2=5,
在Rt△HFP中,∠HPF=90°,HP=3,PF=5,
∴HF= ═
∴GF= .
【解析】【分析】(1)利用“边角边”证明△ADE和△CEF全等,根据全等三角形对应边相等可得AD=CF,然后判断出四边形BCFD是平行四边形,根据平行四边形的性质可得;(2)先判断出△AEG≌△DEH(ASA)进而判断出EF垂直平分GH,即可得出结论;(3)先求出AG=HD= ,进而判断出△PDH为等腰直角三角形,再用勾股定理求出HF即可得出结论.
1 / 1
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
