浙教版数学八年级下册八下第五章 特殊平行四边形 拔尖训练(含答案)
文档属性
| 名称 | 浙教版数学八年级下册八下第五章 特殊平行四边形 拔尖训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 658.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-25 14:15:25 | ||
图片预览

文档简介
八下第五章特殊平行四边形拔尖训练
一、单选题
1.如图,在菱形ABCD中,不一定成立的是( ).
A.四边形ABCD是平行四边形 B.AC⊥BD
C.ABD是等边三角形 D.∠CAB=∠CAD
2.菱形的两条对角线长分别为6与8,则此菱形的面积为( )
A.48 B.20 C.14 D.24
3.矩形、菱形、正方形都具有的性质是( )
A.每一条对角线都平分一组对角 B.对角线相等
C.对角线互相垂直 D.对角线互相平分
4.如图,菱形ABCD中,AC交BD于O, 于点E,连接OE,若 ,则 的度数是( )
A.20° B.30° C.50° D.70°
5.如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,若AC=6,则DE的长为( )
A.3 B. C. D.4
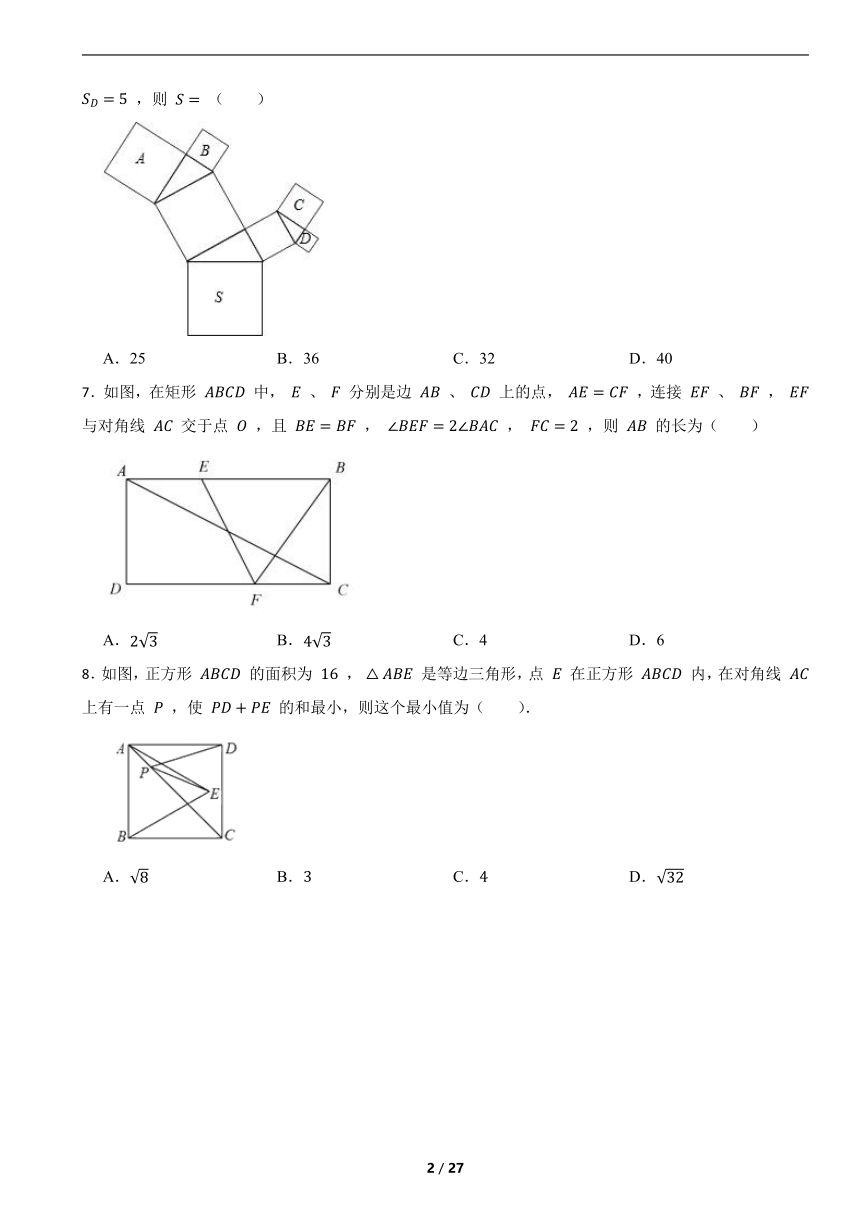
6.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中 , , , ,则 ( )
A.25 B.36 C.32 D.40
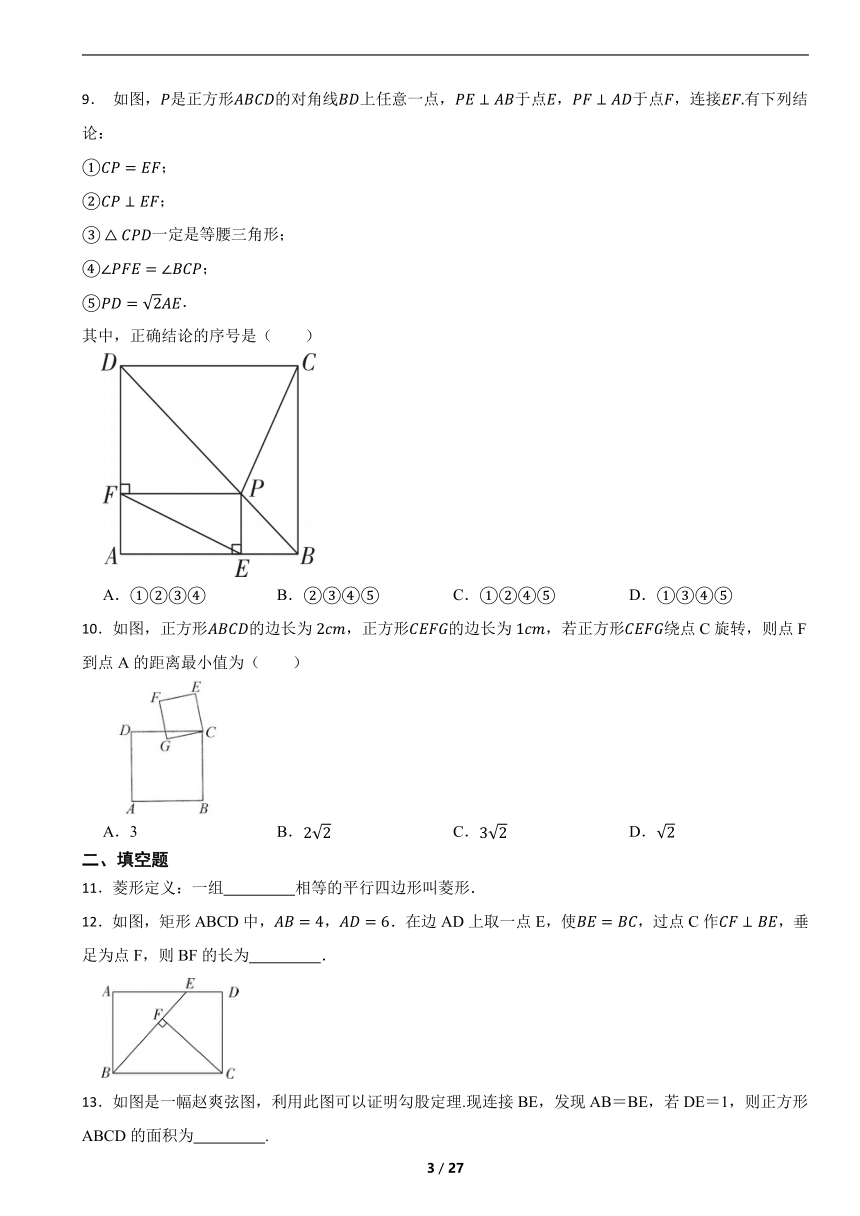
7.如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )
A. B. C.4 D.6
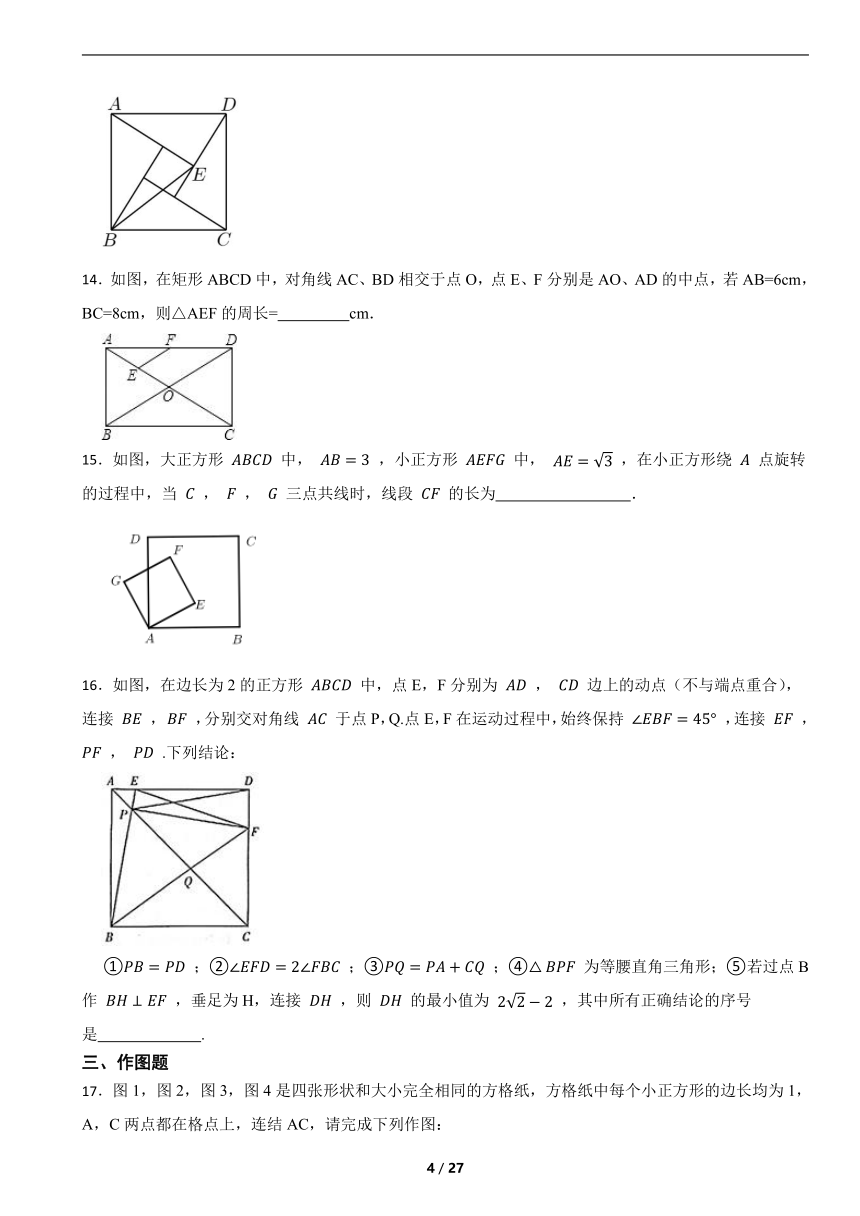
8.如图,正方形 的面积为 , 是等边三角形,点 在正方形 内,在对角线 上有一点 ,使 的和最小,则这个最小值为( ).
A. B. C. D.
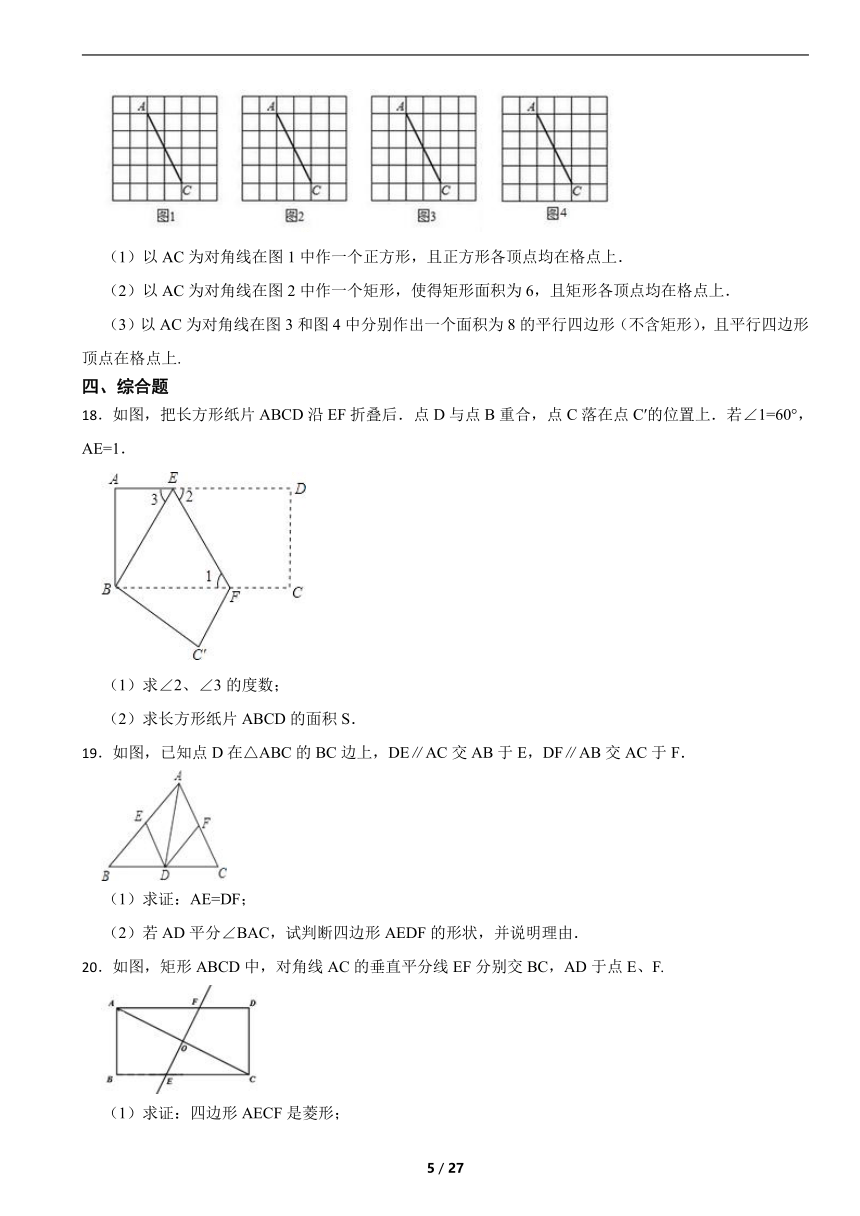
9. 如图,是正方形的对角线上任意一点,于点,于点,连接有下列结论:
;
;
一定是等腰三角形;
;
.
其中,正确结论的序号是( )
A. B. C. D.
10.如图,正方形的边长为,正方形的边长为,若正方形绕点C旋转,则点F到点A的距离最小值为( )
A.3 B. C. D.
二、填空题
11.菱形定义:一组 相等的平行四边形叫菱形.
12.如图,矩形ABCD中,,.在边AD上取一点E,使,过点C作,垂足为点F,则BF的长为 .
13.如图是一幅赵爽弦图,利用此图可以证明勾股定理.现连接BE,发现AB=BE,若DE=1,则正方形ABCD的面积为 .
14.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则△AEF的周长= cm.
15.如图,大正方形 中, ,小正方形 中, ,在小正方形绕 点旋转的过程中,当 , , 三点共线时,线段 的长为 .
16.如图,在边长为2的正方形 中,点E,F分别为 , 边上的动点(不与端点重合),连接 , ,分别交对角线 于点P,Q.点E,F在运动过程中,始终保持 ,连接 , , .下列结论:
① ;② ;③ ;④ 为等腰直角三角形;⑤若过点B作 ,垂足为H,连接 ,则 的最小值为 ,其中所有正确结论的序号是 .
三、作图题
17.图1,图2,图3,图4是四张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,A,C两点都在格点上,连结AC,请完成下列作图:
(1)以AC为对角线在图1中作一个正方形,且正方形各顶点均在格点上.
(2)以AC为对角线在图2中作一个矩形,使得矩形面积为6,且矩形各顶点均在格点上.
(3)以AC为对角线在图3和图4中分别作出一个面积为8的平行四边形(不含矩形),且平行四边形顶点在格点上.
四、综合题
18.如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.
(1)求∠2、∠3的度数;
(2)求长方形纸片ABCD的面积S.
19.如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.
(1)求证:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
20.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E、F.
(1)求证:四边形AECF是菱形;
(2)当BE=3,AF=5时,求AC的长.
21.如图,AC是平行四边形ABCD的对角线,∠BAC=∠DAC.
(1)求证:AB=BC;
(2)若AB=4,AC=4 ,求平行四边形ABCD的面积.
22.如图,在菱形ABCD中,AB=10,S菱形ABCD=60,点E从点B出发在边BC上向终点C运动.过点E作边BC的垂线,交菱形其它的边于点F,在EF的右侧作矩形EFGH.
(1)如图1,点G在AC上.
①求证:FA=FG;
②若点G是AC的中点,求证:BF=FG;
(2)若EF=FG,当EF过AC中点时,求AG的长.
23.已知:在边长为 的正方形 中,点 为对角线 上一点,且 .将三角板的直角顶点与点 重合,一条直角边与直线 交于点 ,另一条直角边与射线 交于点 (点 不与点 重合),将三角板绕点 旋转.
(1)如图,当点 、 在线段 、 上时,求证: ;
(2)当 时,求 的面积;
(3)当 为等腰三角形时,求线段 的长.
五、实践探究题
24.如图,点为正方形内一动点,.过点作,且,连接,.
(1)求证:;
(2)延长交于点,求证:;
(3)在(2)的条件下,若点在运动过程中,存在四边形为平行四边形,试探究此时、满足的数量关系.
答案解析部分
1.【答案】C
【解析】【解答】菱形是特殊的平行四边形,故A正确,根据菱形的性质:对角线互相平分且平分对角得B、D正确,所以选C.
【分析】此题主要考查菱形的基本性质:菱形的对角线互相垂直平分,且每一条对角线平分一组对角;以及和平行四边形的联系.
2.【答案】D
【解析】【解答】6×8÷2=24
故答案为:D.
【分析】根据S菱形等于两对角线乘积的一半可求解.
3.【答案】D
【解析】【解答】解: 矩形、菱形、正方形都具有的性质是:对角线互相平分,
故答案为:D.
【分析】根据矩形、菱形、正方形的性质判断求解即可。
4.【答案】A
【解析】【解答】解:∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,AB=BC,AO=OC,
∵ ,
∴∠ABD= ∠ABC=∠CDB=20°,
∴∠OCD=70°,
∵AE⊥DC,
∴∠EAC+∠OCD=90°,
∴∠EAC=20°,
∵在Rt△AEC中,AO=OC,
∴OE=OA,
∴∠OEA=∠EAC=20°.
所以答案为A选项.
【分析】根据菱形的基本性质得出∠ABD=∠CDB=20°,然后进一步得出∠EAC的度数,最后根据直角三角形斜边中线性质得出OA=OE,从而进一步得出答案即可.
5.【答案】A
【解析】【解答】解:∵E为AB的中点,DE⊥AB,
∴AD=DB,
∵四边形ABCD是菱形,
∴AB=AD,
∴AD=DB=AB,
∴△ABD为等边三角形.
∵四边形ABCD是菱形,
∴BD⊥AC于O,AO= AC= ×6=3,
由(1)可知DE和AO都是等边△ABD的高,
∴DE=AO=3.
故答案为:A
【分析】根据菱形的性质,可判断出△ABD为等边三角形,得出DE的长度。
6.【答案】B
【解析】【解答】解:根据勾股定理的几何意义,可知:
S=SF+SG
=SA+SB+SC+SD
=36;
故答案为:B.
【分析】根据正方形的性质和勾股定理的几何意义解答即可.
7.【答案】D
【解析】【解答】解:如图,连接BO,
∵四边形ABCD是矩形,
∴DC∥AB,∠DCB=90°
∴∠FCO=∠EAO,
在△AOE和△COF中,
,
∴△AOE≌△COF,
∴OE=OF,OA=OC,
∵BF=BE,
∴BO⊥EF,∠BOF=90°,
∵∠FEB=2∠CAB=∠CAB+∠AOE,
∴∠EAO=∠EOA,
∴EA=EO=OF=FC=2,
在Rt△BFO和Rt△BFC中,
,
∴Rt△BFO≌Rt△BFC,
∴BO=BC,
在Rt△ABC中,∵AO=OC,
∴BO=AO=OC=BC,
∴△BOC是等边三角形,
∴∠BCO=60°,∠BAC=30°,
∴∠FEB=2∠CAB=60°,
∵BE=BF,
∴△BEF是等边三角形,
∴EB=EF=4,
∴AB=AE+EB=2+4=6.
故答案为:D.
【分析】连接BO,根据矩形的性质可得DC∥AB,∠DCB=90°,根据平行线的性质可得∠FCO=∠EAO,证明△AOE≌△COF,得到OE=OF,OA=OC,推出∠EAO=∠EOA,则EA=EO=OF=FC=2,证明Rt△BFO≌Rt△BFC,得到BO=BC,易得△BOC是等边三角形,得到∠BCO=60°,∠BAC=30°,则∠FEB=2∠CAB=60°,进而推出△BEF是等边三角形,则EB=EF=4,然后根据AB=AE+EB进行计算.
8.【答案】C
【解析】【解答】连接 、 、 关于 AC 对称.
∴ .
∴ ,当 、 、 三点共线得 最小.
∴ ,选C.
【分析】连接 、 ,由于 关于 对称,可得PB=PD,由于,可得当 、 、 三点共线得 最小,最小值等于BE的长,据此解答即可.
9.【答案】B
【解析】【解答】解:过作于点,
点是正方形的对角线上一点,
,
在中,,
,
,
同理,得
,
,
,,
,
≌,
;
,
延长到上于一点,
,
,
,即;
点是正方形的对角线上任意一点,度,
当度或度或度时,是等腰三角形,
除此之外,不是等腰三角形,故错误.
,
,
又,
,
,
在中,,
.
其中正确结论的序号是.
故选:.
【分析】根据正方形的性质,全等三角形的判定定理及性质,等腰三角形的判定定理及勾股定理即可求出答案。
10.【答案】D
【解析】【解答】解:当点F在正方形的对角线AC上时,由三角形三边关系可知,
当点F不在正方形的对角线AC上时,由三角形三边关系可知,
∴当点F在正方形的对角线AC上时,点F到点A的距离最小值.
∵正方形的边长为,正方形的边长为,
,
∴,
故答案为:D.
【分析】当F在对角线AC上时,点F到点A的距离最小,根据AF=AC-CF即可求解.
11.【答案】邻边
【解析】【解答】解:由题意知,一组邻边相等的平行四边形叫菱形;
故答案为:邻边.
【分析】由菱形的定义可得答案。
12.【答案】
【解析】【解答】解:如图,连接CE,
∵四边形ABCD是矩形,
∴AD=BC=6,
∵BE=BC,
∴BE=6,
∵S△BCE=BC·AB=BE·CF,
∴6×4=6CF,
∴CF=4,
在Rt△BFC中,由勾股定理得.
故答案为:.
【分析】根据矩形的性质及已知可得BE=6,由等面积法可得S△BCE=BC·AB=BE·CF,据此建立方程可求出CF的长,进而在Rt△BFC中,利用勾股定理可算出BF的长.
13.【答案】5
【解析】【解答】解:如图:由题意得,,
,,
,
,
正方形的面积,
故答案为:5.
【分析】由题意得AH=DE=1,由等腰三角形的性质可得AE=2BH=2AH=2,由勾股定理可求出AB的值,进而可得正方形ABCD的面积.
14.【答案】9
【解析】【解答】解:在Rt△ABC中,AC= =10cm,
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,EF= OD= BD= AC= cm,AF= AD= BC=4cm,AE= AO= AC= cm,
∴△AEF的周长=AE+AF+EF=9cm.
故答案为:9.
【分析】先求出矩形的对角线AC,根据中位线定理可得出EF,继而可得出△AEF的周长.
15.【答案】 或
【解析】【解答】连接AC,
∵正方形 中, ,
∴ ;
∵正方形 中, ,
∴ ;
当 , , 三点共线时,如图1,
在Rt△AGC中, ,
∴ ;
当 , , 三点共线时,如图2,
在Rt△AGC中, ,
∴ .
综上,CF的长为 或 .
故答案为: 或 .
【分析】分两种情况,再结合图象利用勾股定理求解即可。
16.【答案】①②④⑤
【解析】【解答】解:如图,连接BD,
∵正方形ABCD,
∴AP与BD互相垂直平分,
∴PB=PD,
∴①符合题意;
如图,延长DA使得AK=CF,连接BK,
又∵AB=BC,∠BAK=∠BCF=90°,
∴△BAK≌△BCF(SAS),
∴∠CBF=∠ABK,BK=BF,∠K=∠BFC,
∵∠EBF=45°,
∴∠ABE+∠CBF=45°,
∴∠KBF=∠ABK+∠ABE=45°,
∴∠EBK=∠EBF,
∴△EBK≌△EBF(SAS),
∴∠K=∠EFB,∠KEB=∠FEB,
∴∠EFB=∠BFC,
∴∠EFD=180°-(∠EFB+∠BFC)=180°-2∠BFC=180°-2(90°-∠FBC),
∴∠EFD=2∠FBC
∴②符合题意;
如图,作∠CBG=∠ABP,使得BG=BP,与AC的延长线交于点M,连接CG,
∴∠PBM=∠ABC=90°,
∵∠BPM>45°,
∴∠GMC<45°,
易证△ABP≌△CBG(SAS),
∴∠BAP=∠BCG=45°,
∴∠GCM=∠PCG=90°,
∴GC≠CM,即AP≠CM,
∴PQ≠PA+CQ,
∴③不符合题意;
∵正方形ABCD,
∴∠EBF=∠BCP=∠FCP=45°,∠PQB=∠FQC,
∴△BQP∽△CQF,
∴BQ:CQ=PQ:FQ,
又∵∠BQC=∠PQF,
∴∠BCQ=∠PFQ=45°,
∴∠PBF=∠PFB=45°,
∴△BPF是等腰直角三角形,
∴④符合题意;
如图所示,连接BD,
∴当点B、H、D三点共线时,DH的值最小,
∵BC=CD=BA=AD=2,
∴BD=2,
∵∠EPF=∠EDF=90°,
∴E,D,F,P四点共圆,
∴∠PEF=∠PDF,
∵PB=PD=PF,
∴∠PDF=∠PFD,
∵∠AEB+∠DEP=180°,∠DEP+∠DFP=180°,
∴∠AEB=∠DFP=∠PDF=∠PEF,
∴∠AEB=∠BEH,
∵BH⊥EF,
∴∠BAE=∠BHE=90°,
∵BE=BE,
∴△BEA≌△BEH(AAS),
∴BA=BH=2,
∴DHmin=BD-BH=2-2.
∴正确的有①②④⑤.
故答案为:①②④⑤
【分析】如图,连接BD,根据正方形性质及线段垂直平分线的性质易得PB=PD,故①符合题意;如图,延长DA使得AK=CF,连接BK,先由“SAS”定理证出△BAK≌△BCF,得∠CBF=∠ABK,BK=BF,∠K=∠BFC,通过角的和差关系推出∠EBK=∠EBF,由“SAS”定理证出△EBK≌△EBF,得∠K=∠EFB,∠KEB=∠FEB,从而得∠EFB=∠BFC,通过角的互补关系及角的和差关系推出∠EFD=2∠FBC,故②符合题意;作∠CBG=∠ABP,使得BG=BP,与AC延长线交于点M,连接CG,由∠PBM=∠ABC=90°,则∠BPM>45°,∠GMC<45°,易证△ABP≌△CBG,得∠BAP=∠BCG=45°,∠GCM=∠PCG=90°,可知GC≠CM,即AP≠CM,PQ≠PA+CQ,故③不符合题意;由两组角相等易证出△BQP∽△CQF,由相似性质及角的等量关系可得∠PBF=∠PFB=45°,即得出△BPF是等腰直角三角形,故④符合题意;如图所示,连接BD,当点B、H、D三点共线时,DH值最小,易求得BD=2,根据∠EPF=∠EDF=90°,则E,D,F,P四点共圆,由圆周角定理和角的等量关系代换可得∠AEB=∠BEH,又∠BAE=∠BHE=90°,BE=BE,即证出△BEA≌△BEH,可得BA=BH=2,再由DHmin=BD-BH,代入数据计算即可求解.
17.【答案】(1)解:如图所示:
(2)解:如图所示:
(3)解:如图所示,
【解析】【分析】(1)利用正方形的性质和格点特点,画出以AC为对角线的格点正方形.
(2)利用矩形的面积等于长×宽,画出以AC为对角线的格点矩形的面积为6即可.
(3)利用平行四边形的面积公式,可知对角线分得的一个三角形的面积为4,由此可画出以AC为对角线的面积为8的格点矩形.
18.【答案】(1)解:如图,∵AD∥BC,∴∠2=∠1=60°;又∵∠4=∠2=60°,
∴∠3=180°﹣60°﹣60°=60°
(2)解:在直角△ABE中,由(1)知∠3=60°,
∴∠5=90°﹣60°=30°;
∴BE=2AE=2,
∴AB= = ;
∴AD=AE+DE=AE+BE=1+2=3,
∴长方形纸片ABCD的面积S为:AB AD= ×3=3 .
【解析】【分析】(1)根据矩形的性质得出AD∥BC,由二直线平行内错角相等得出∠2=∠1=60°;根据折叠的性质∠4=∠2=60°,根据平角的定义得出∠3的度数;
(2)根据矩形的性质得出∠A=90°,根据三角形的内角和得出∠5=30°,根据含30°直角三角形的边之间的关系得出BE的长,根据勾股定理算出AB的长,由AD=AE+DE算出AD的长,根据矩形的面积计算方法即可算出答案。
19.【答案】(1)证明:∵DE∥AC,∠ADE=∠DAF,同理∠DAE=∠FDA,
∵AD=DA,
∴△ADE≌△DAF( ASA ),
∴AE=DF
(2)解:若AD平分∠BAC,四边形AEDF是菱形,∵DE∥AC,DF∥AB,∴四边形AEDF是平行四边形,∵若AD平分∠BAC∴∠EAD=∠DAF,又∵∠ADE=∠DAF,
∴∠EAD=∠ADE
∴AE=DE.
∴平行四边形AEDF为菱形
【解析】【分析】(1)根据二直线平行,内错角相等得出∠ADE=∠DAF,∠DAE=∠FDA,又AD=DA,根据ASA判断出△ADE≌△DAF,根据全等三角形对应边相等得出AE=DF
(2)若AD平分∠BAC,四边形AEDF是菱形,根据两组对边分别平行的四边形是平行四边形得出四边形AEDF是平行四边形,根据角的平分线,及等量代换得出∠EAD=∠ADE,根据等角对等边得出AE=DE.根据有一组邻边相等的平行四边形是菱形即可得出结论。
20.【答案】(1)证明:如图,连接AE,CF,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵EF垂直平分AC,
∴AF=FC,AE=EC,
∴∠FAC=∠FCA,
∴∠FCA=∠ACB,
∵∠FCA+∠CFE=90°,∠ACB+∠CEF=90°,
∴∠CFE=∠CEF,
∴CE=CF,
∴AF=FC=CE=AE,
∴四边形AECF是菱形;
(2)解:∵四边形AECF是菱形,AF=5,
∴CE=AF=AE=5,
由∠B=90°,
∴在Rt△ABE中,
AB= .
∵BC=BE+EC=8,
【解析】【分析】(1)根据四边相等的四边形是菱形即可判断;(2)在Rt△ABE中,利用勾股定理可求得AB的长,在Rt△ABC中,利用勾股定理解答即可.
21.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠BCA,
∵∠BAC=∠DAC,
∴∠BAC=∠BCA,
∴AB=BC;
(2)解:连接BD交AC于O,如图所示:
∵四边形ABCD是平行四边形,AB=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,OA=OC= AC=2 ,OB=OD= BD,
∴OB= ═2,
∴BD=2OB=4,
∴平行四边形ABCD的面积= AC BD= ×
【解析】【分析】(1)根据平行四边形的性质得出AD∥BC,根据平行线的性质得出∠DAC=∠BCA,求出∠BAC=∠BCA即可;(2)求出四边形ABCD是菱形,根据勾股定理求出BO,求出BD,根据面积公式求出即可.
22.【答案】(1)①证明:∵菱形ABCD,
∴AB=BC,
∴∠BAC=∠BCA,
∵矩形EFGH,
∴FG∥EH,
∴∠EGA=∠BCA,
∴∠BAC=∠EGA,即∠FAG=∠EGA,
∴FA=FG;
②解:如图1,连接BG,
∵FG∥BC,G为AC中点,
∴FG为△ABC中位线,
∴F为AB的中点,
∵G为AC中点,BA=BC,
∴BG⊥AC,即∠BGA=90°,
∴FG=BF.
(2)解:如图2,点E在BC上运动,过点E作边BC的垂线EF交AD于点F,交AC于点O,在EF的右侧作矩形EFGH,再过点A作AM⊥BC于点M,
∵S菱形ABCD=60,AB=10
∴S△ABC=30,BC=10,
∴AM=6,
∴BM==8,
∴MC=2,
∵矩形EFGH,
∵AF∥EC,AM⊥ME,
∴四边形AMEF为矩形,
∴AF=ME,AF∥ME,
又∵∠AOF=∠COE,OA=OC,
∴△AOF≌△COE(AAS),
∴AF=EC,
∴ME=EC=1,
∴AF=1,
又∵EF=FG,EF=AM=6,
∴AG=AF+FG=1+6=7.
【解析】【分析】(1)①由菱形性质推出∠BAC=∠BCA,由矩形性质推出∠EGA=∠BCA,即得∠BAC=∠EGA,从而得∠FAG=∠EGA,进而推出FA=FG;②如图1,连接BG,易得FG为△ABC中位线,即得F为AB的中点,再由等腰三角形三线合一可得BG⊥AC,即∠BGA=90°,再由直角三角形斜边上中线等于斜边一半即可推出FG=BF;
(2)如图2,点E在BC上运动,过点E作边BC的垂线EF交AD于点F,交AC于点O,在EF的右侧作矩形EFGH,再过点A作AM⊥BC于点M,由菱形性质推出S△ABC=30,BC=10,由三角形面积公式可计算出AM=6,由勾股定理求得BM=8,从而得MC=2,由矩形AMEF性质,易推出四边形AMEF为矩形,则AF=ME,AF∥ME,又∠AOF=∠COE,OA=OC,可推出△AOF≌△COE,即得AF=EC,求得AF=1,再根据EF=FG,EF=AM=6,代入AG=AF+FG中,即可求出AG的长.
23.【答案】(1)解:如图1,过点 作 , ,垂足分别为点 、 .
四边形 为正方形,
, .
.
四边形 为正方形.
,
∵ ,
,
即 .
在 和 中,
.
.
(2)解:如图2,过点 作 ,垂足为点 ,
当 时, ,
在 中,设 ,则 , .
在 中, , .
,
.
.
(3)解:(一)当点 在 延长线上时,
因为 ,
所以只有 .
如图3,同理可证: ,
.
,
.
.
(二)当点 在射线 上时,
①如图4, ,
,
,
.
② .
,
,
此时,点 和点 重合,舍去.
③如图5, .同理可证: ,
.
.
综上所述, 的长为 , 或 .
【解析】【分析】(1)先求出 , 再证明三角形全等求解即可;
(2)利用勾股定理和三角形的面积公式计算求解即可;
(3)分类讨论,结合图形,利用全等三角形的性质求解即可。
24.【答案】(1)证明:四边形是正方形,
,,
,,
,
又,
,
(2)证明:如图,延长交于点,
,
,
,
,
,
四边形是矩形,
又,
矩形是正方形,
;
(3)证明:.理由如下:
如图,过点作交于,
,
,
,
,
,
,
又,,
,
,
,,
四边形是正方形,四边形为平行四边形,
,
又,
,
,
,
.
【解析】【分析】⑴、论证两角相等,结合图形考虑证明两角所在三角形全等。由四边形ABCD是正方形可知AB=CB,∠ABC=90°,又BG⊥BE,所以∠EBG=90°,利用同角的余角相等可得∠ABE=∠CBG,又BG=BE,由边角边论证三角形ABE和三角形CBG全等,由全等三角形性质可得结论。
⑵、由图知EF和BE同属于同一个四边形的两边,所以考虑证明四边形BEFG是正方形或菱形,由题易知四边形有三个角是直角,且有一组邻边相等,易证四边形BEFG是正方形,所以EF=EB成立。
⑶、猜想DE=CD,所以论证DE等于正方形ABCD的边长即可。通过添加辅助线DK⊥AE,和连接EC、BF,论证△DAK≌△ABE≌△CBG;又四边形CEBF是平行四边形,可得CF=BE,可论证DK=AE,∠DKE=∠AEB,KE=EB,所以△DKE≌△AEB,利用全等三角形性质得DE=AB,又AB=CD,等量代换即可得结论。
1 / 1
一、单选题
1.如图,在菱形ABCD中,不一定成立的是( ).
A.四边形ABCD是平行四边形 B.AC⊥BD
C.ABD是等边三角形 D.∠CAB=∠CAD
2.菱形的两条对角线长分别为6与8,则此菱形的面积为( )
A.48 B.20 C.14 D.24
3.矩形、菱形、正方形都具有的性质是( )
A.每一条对角线都平分一组对角 B.对角线相等
C.对角线互相垂直 D.对角线互相平分
4.如图,菱形ABCD中,AC交BD于O, 于点E,连接OE,若 ,则 的度数是( )
A.20° B.30° C.50° D.70°
5.如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,若AC=6,则DE的长为( )
A.3 B. C. D.4
6.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中 , , , ,则 ( )
A.25 B.36 C.32 D.40
7.如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )
A. B. C.4 D.6
8.如图,正方形 的面积为 , 是等边三角形,点 在正方形 内,在对角线 上有一点 ,使 的和最小,则这个最小值为( ).
A. B. C. D.
9. 如图,是正方形的对角线上任意一点,于点,于点,连接有下列结论:
;
;
一定是等腰三角形;
;
.
其中,正确结论的序号是( )
A. B. C. D.
10.如图,正方形的边长为,正方形的边长为,若正方形绕点C旋转,则点F到点A的距离最小值为( )
A.3 B. C. D.
二、填空题
11.菱形定义:一组 相等的平行四边形叫菱形.
12.如图,矩形ABCD中,,.在边AD上取一点E,使,过点C作,垂足为点F,则BF的长为 .
13.如图是一幅赵爽弦图,利用此图可以证明勾股定理.现连接BE,发现AB=BE,若DE=1,则正方形ABCD的面积为 .
14.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则△AEF的周长= cm.
15.如图,大正方形 中, ,小正方形 中, ,在小正方形绕 点旋转的过程中,当 , , 三点共线时,线段 的长为 .
16.如图,在边长为2的正方形 中,点E,F分别为 , 边上的动点(不与端点重合),连接 , ,分别交对角线 于点P,Q.点E,F在运动过程中,始终保持 ,连接 , , .下列结论:
① ;② ;③ ;④ 为等腰直角三角形;⑤若过点B作 ,垂足为H,连接 ,则 的最小值为 ,其中所有正确结论的序号是 .
三、作图题
17.图1,图2,图3,图4是四张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,A,C两点都在格点上,连结AC,请完成下列作图:
(1)以AC为对角线在图1中作一个正方形,且正方形各顶点均在格点上.
(2)以AC为对角线在图2中作一个矩形,使得矩形面积为6,且矩形各顶点均在格点上.
(3)以AC为对角线在图3和图4中分别作出一个面积为8的平行四边形(不含矩形),且平行四边形顶点在格点上.
四、综合题
18.如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.
(1)求∠2、∠3的度数;
(2)求长方形纸片ABCD的面积S.
19.如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.
(1)求证:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
20.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E、F.
(1)求证:四边形AECF是菱形;
(2)当BE=3,AF=5时,求AC的长.
21.如图,AC是平行四边形ABCD的对角线,∠BAC=∠DAC.
(1)求证:AB=BC;
(2)若AB=4,AC=4 ,求平行四边形ABCD的面积.
22.如图,在菱形ABCD中,AB=10,S菱形ABCD=60,点E从点B出发在边BC上向终点C运动.过点E作边BC的垂线,交菱形其它的边于点F,在EF的右侧作矩形EFGH.
(1)如图1,点G在AC上.
①求证:FA=FG;
②若点G是AC的中点,求证:BF=FG;
(2)若EF=FG,当EF过AC中点时,求AG的长.
23.已知:在边长为 的正方形 中,点 为对角线 上一点,且 .将三角板的直角顶点与点 重合,一条直角边与直线 交于点 ,另一条直角边与射线 交于点 (点 不与点 重合),将三角板绕点 旋转.
(1)如图,当点 、 在线段 、 上时,求证: ;
(2)当 时,求 的面积;
(3)当 为等腰三角形时,求线段 的长.
五、实践探究题
24.如图,点为正方形内一动点,.过点作,且,连接,.
(1)求证:;
(2)延长交于点,求证:;
(3)在(2)的条件下,若点在运动过程中,存在四边形为平行四边形,试探究此时、满足的数量关系.
答案解析部分
1.【答案】C
【解析】【解答】菱形是特殊的平行四边形,故A正确,根据菱形的性质:对角线互相平分且平分对角得B、D正确,所以选C.
【分析】此题主要考查菱形的基本性质:菱形的对角线互相垂直平分,且每一条对角线平分一组对角;以及和平行四边形的联系.
2.【答案】D
【解析】【解答】6×8÷2=24
故答案为:D.
【分析】根据S菱形等于两对角线乘积的一半可求解.
3.【答案】D
【解析】【解答】解: 矩形、菱形、正方形都具有的性质是:对角线互相平分,
故答案为:D.
【分析】根据矩形、菱形、正方形的性质判断求解即可。
4.【答案】A
【解析】【解答】解:∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,AB=BC,AO=OC,
∵ ,
∴∠ABD= ∠ABC=∠CDB=20°,
∴∠OCD=70°,
∵AE⊥DC,
∴∠EAC+∠OCD=90°,
∴∠EAC=20°,
∵在Rt△AEC中,AO=OC,
∴OE=OA,
∴∠OEA=∠EAC=20°.
所以答案为A选项.
【分析】根据菱形的基本性质得出∠ABD=∠CDB=20°,然后进一步得出∠EAC的度数,最后根据直角三角形斜边中线性质得出OA=OE,从而进一步得出答案即可.
5.【答案】A
【解析】【解答】解:∵E为AB的中点,DE⊥AB,
∴AD=DB,
∵四边形ABCD是菱形,
∴AB=AD,
∴AD=DB=AB,
∴△ABD为等边三角形.
∵四边形ABCD是菱形,
∴BD⊥AC于O,AO= AC= ×6=3,
由(1)可知DE和AO都是等边△ABD的高,
∴DE=AO=3.
故答案为:A
【分析】根据菱形的性质,可判断出△ABD为等边三角形,得出DE的长度。
6.【答案】B
【解析】【解答】解:根据勾股定理的几何意义,可知:
S=SF+SG
=SA+SB+SC+SD
=36;
故答案为:B.
【分析】根据正方形的性质和勾股定理的几何意义解答即可.
7.【答案】D
【解析】【解答】解:如图,连接BO,
∵四边形ABCD是矩形,
∴DC∥AB,∠DCB=90°
∴∠FCO=∠EAO,
在△AOE和△COF中,
,
∴△AOE≌△COF,
∴OE=OF,OA=OC,
∵BF=BE,
∴BO⊥EF,∠BOF=90°,
∵∠FEB=2∠CAB=∠CAB+∠AOE,
∴∠EAO=∠EOA,
∴EA=EO=OF=FC=2,
在Rt△BFO和Rt△BFC中,
,
∴Rt△BFO≌Rt△BFC,
∴BO=BC,
在Rt△ABC中,∵AO=OC,
∴BO=AO=OC=BC,
∴△BOC是等边三角形,
∴∠BCO=60°,∠BAC=30°,
∴∠FEB=2∠CAB=60°,
∵BE=BF,
∴△BEF是等边三角形,
∴EB=EF=4,
∴AB=AE+EB=2+4=6.
故答案为:D.
【分析】连接BO,根据矩形的性质可得DC∥AB,∠DCB=90°,根据平行线的性质可得∠FCO=∠EAO,证明△AOE≌△COF,得到OE=OF,OA=OC,推出∠EAO=∠EOA,则EA=EO=OF=FC=2,证明Rt△BFO≌Rt△BFC,得到BO=BC,易得△BOC是等边三角形,得到∠BCO=60°,∠BAC=30°,则∠FEB=2∠CAB=60°,进而推出△BEF是等边三角形,则EB=EF=4,然后根据AB=AE+EB进行计算.
8.【答案】C
【解析】【解答】连接 、 、 关于 AC 对称.
∴ .
∴ ,当 、 、 三点共线得 最小.
∴ ,选C.
【分析】连接 、 ,由于 关于 对称,可得PB=PD,由于,可得当 、 、 三点共线得 最小,最小值等于BE的长,据此解答即可.
9.【答案】B
【解析】【解答】解:过作于点,
点是正方形的对角线上一点,
,
在中,,
,
,
同理,得
,
,
,,
,
≌,
;
,
延长到上于一点,
,
,
,即;
点是正方形的对角线上任意一点,度,
当度或度或度时,是等腰三角形,
除此之外,不是等腰三角形,故错误.
,
,
又,
,
,
在中,,
.
其中正确结论的序号是.
故选:.
【分析】根据正方形的性质,全等三角形的判定定理及性质,等腰三角形的判定定理及勾股定理即可求出答案。
10.【答案】D
【解析】【解答】解:当点F在正方形的对角线AC上时,由三角形三边关系可知,
当点F不在正方形的对角线AC上时,由三角形三边关系可知,
∴当点F在正方形的对角线AC上时,点F到点A的距离最小值.
∵正方形的边长为,正方形的边长为,
,
∴,
故答案为:D.
【分析】当F在对角线AC上时,点F到点A的距离最小,根据AF=AC-CF即可求解.
11.【答案】邻边
【解析】【解答】解:由题意知,一组邻边相等的平行四边形叫菱形;
故答案为:邻边.
【分析】由菱形的定义可得答案。
12.【答案】
【解析】【解答】解:如图,连接CE,
∵四边形ABCD是矩形,
∴AD=BC=6,
∵BE=BC,
∴BE=6,
∵S△BCE=BC·AB=BE·CF,
∴6×4=6CF,
∴CF=4,
在Rt△BFC中,由勾股定理得.
故答案为:.
【分析】根据矩形的性质及已知可得BE=6,由等面积法可得S△BCE=BC·AB=BE·CF,据此建立方程可求出CF的长,进而在Rt△BFC中,利用勾股定理可算出BF的长.
13.【答案】5
【解析】【解答】解:如图:由题意得,,
,,
,
,
正方形的面积,
故答案为:5.
【分析】由题意得AH=DE=1,由等腰三角形的性质可得AE=2BH=2AH=2,由勾股定理可求出AB的值,进而可得正方形ABCD的面积.
14.【答案】9
【解析】【解答】解:在Rt△ABC中,AC= =10cm,
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,EF= OD= BD= AC= cm,AF= AD= BC=4cm,AE= AO= AC= cm,
∴△AEF的周长=AE+AF+EF=9cm.
故答案为:9.
【分析】先求出矩形的对角线AC,根据中位线定理可得出EF,继而可得出△AEF的周长.
15.【答案】 或
【解析】【解答】连接AC,
∵正方形 中, ,
∴ ;
∵正方形 中, ,
∴ ;
当 , , 三点共线时,如图1,
在Rt△AGC中, ,
∴ ;
当 , , 三点共线时,如图2,
在Rt△AGC中, ,
∴ .
综上,CF的长为 或 .
故答案为: 或 .
【分析】分两种情况,再结合图象利用勾股定理求解即可。
16.【答案】①②④⑤
【解析】【解答】解:如图,连接BD,
∵正方形ABCD,
∴AP与BD互相垂直平分,
∴PB=PD,
∴①符合题意;
如图,延长DA使得AK=CF,连接BK,
又∵AB=BC,∠BAK=∠BCF=90°,
∴△BAK≌△BCF(SAS),
∴∠CBF=∠ABK,BK=BF,∠K=∠BFC,
∵∠EBF=45°,
∴∠ABE+∠CBF=45°,
∴∠KBF=∠ABK+∠ABE=45°,
∴∠EBK=∠EBF,
∴△EBK≌△EBF(SAS),
∴∠K=∠EFB,∠KEB=∠FEB,
∴∠EFB=∠BFC,
∴∠EFD=180°-(∠EFB+∠BFC)=180°-2∠BFC=180°-2(90°-∠FBC),
∴∠EFD=2∠FBC
∴②符合题意;
如图,作∠CBG=∠ABP,使得BG=BP,与AC的延长线交于点M,连接CG,
∴∠PBM=∠ABC=90°,
∵∠BPM>45°,
∴∠GMC<45°,
易证△ABP≌△CBG(SAS),
∴∠BAP=∠BCG=45°,
∴∠GCM=∠PCG=90°,
∴GC≠CM,即AP≠CM,
∴PQ≠PA+CQ,
∴③不符合题意;
∵正方形ABCD,
∴∠EBF=∠BCP=∠FCP=45°,∠PQB=∠FQC,
∴△BQP∽△CQF,
∴BQ:CQ=PQ:FQ,
又∵∠BQC=∠PQF,
∴∠BCQ=∠PFQ=45°,
∴∠PBF=∠PFB=45°,
∴△BPF是等腰直角三角形,
∴④符合题意;
如图所示,连接BD,
∴当点B、H、D三点共线时,DH的值最小,
∵BC=CD=BA=AD=2,
∴BD=2,
∵∠EPF=∠EDF=90°,
∴E,D,F,P四点共圆,
∴∠PEF=∠PDF,
∵PB=PD=PF,
∴∠PDF=∠PFD,
∵∠AEB+∠DEP=180°,∠DEP+∠DFP=180°,
∴∠AEB=∠DFP=∠PDF=∠PEF,
∴∠AEB=∠BEH,
∵BH⊥EF,
∴∠BAE=∠BHE=90°,
∵BE=BE,
∴△BEA≌△BEH(AAS),
∴BA=BH=2,
∴DHmin=BD-BH=2-2.
∴正确的有①②④⑤.
故答案为:①②④⑤
【分析】如图,连接BD,根据正方形性质及线段垂直平分线的性质易得PB=PD,故①符合题意;如图,延长DA使得AK=CF,连接BK,先由“SAS”定理证出△BAK≌△BCF,得∠CBF=∠ABK,BK=BF,∠K=∠BFC,通过角的和差关系推出∠EBK=∠EBF,由“SAS”定理证出△EBK≌△EBF,得∠K=∠EFB,∠KEB=∠FEB,从而得∠EFB=∠BFC,通过角的互补关系及角的和差关系推出∠EFD=2∠FBC,故②符合题意;作∠CBG=∠ABP,使得BG=BP,与AC延长线交于点M,连接CG,由∠PBM=∠ABC=90°,则∠BPM>45°,∠GMC<45°,易证△ABP≌△CBG,得∠BAP=∠BCG=45°,∠GCM=∠PCG=90°,可知GC≠CM,即AP≠CM,PQ≠PA+CQ,故③不符合题意;由两组角相等易证出△BQP∽△CQF,由相似性质及角的等量关系可得∠PBF=∠PFB=45°,即得出△BPF是等腰直角三角形,故④符合题意;如图所示,连接BD,当点B、H、D三点共线时,DH值最小,易求得BD=2,根据∠EPF=∠EDF=90°,则E,D,F,P四点共圆,由圆周角定理和角的等量关系代换可得∠AEB=∠BEH,又∠BAE=∠BHE=90°,BE=BE,即证出△BEA≌△BEH,可得BA=BH=2,再由DHmin=BD-BH,代入数据计算即可求解.
17.【答案】(1)解:如图所示:
(2)解:如图所示:
(3)解:如图所示,
【解析】【分析】(1)利用正方形的性质和格点特点,画出以AC为对角线的格点正方形.
(2)利用矩形的面积等于长×宽,画出以AC为对角线的格点矩形的面积为6即可.
(3)利用平行四边形的面积公式,可知对角线分得的一个三角形的面积为4,由此可画出以AC为对角线的面积为8的格点矩形.
18.【答案】(1)解:如图,∵AD∥BC,∴∠2=∠1=60°;又∵∠4=∠2=60°,
∴∠3=180°﹣60°﹣60°=60°
(2)解:在直角△ABE中,由(1)知∠3=60°,
∴∠5=90°﹣60°=30°;
∴BE=2AE=2,
∴AB= = ;
∴AD=AE+DE=AE+BE=1+2=3,
∴长方形纸片ABCD的面积S为:AB AD= ×3=3 .
【解析】【分析】(1)根据矩形的性质得出AD∥BC,由二直线平行内错角相等得出∠2=∠1=60°;根据折叠的性质∠4=∠2=60°,根据平角的定义得出∠3的度数;
(2)根据矩形的性质得出∠A=90°,根据三角形的内角和得出∠5=30°,根据含30°直角三角形的边之间的关系得出BE的长,根据勾股定理算出AB的长,由AD=AE+DE算出AD的长,根据矩形的面积计算方法即可算出答案。
19.【答案】(1)证明:∵DE∥AC,∠ADE=∠DAF,同理∠DAE=∠FDA,
∵AD=DA,
∴△ADE≌△DAF( ASA ),
∴AE=DF
(2)解:若AD平分∠BAC,四边形AEDF是菱形,∵DE∥AC,DF∥AB,∴四边形AEDF是平行四边形,∵若AD平分∠BAC∴∠EAD=∠DAF,又∵∠ADE=∠DAF,
∴∠EAD=∠ADE
∴AE=DE.
∴平行四边形AEDF为菱形
【解析】【分析】(1)根据二直线平行,内错角相等得出∠ADE=∠DAF,∠DAE=∠FDA,又AD=DA,根据ASA判断出△ADE≌△DAF,根据全等三角形对应边相等得出AE=DF
(2)若AD平分∠BAC,四边形AEDF是菱形,根据两组对边分别平行的四边形是平行四边形得出四边形AEDF是平行四边形,根据角的平分线,及等量代换得出∠EAD=∠ADE,根据等角对等边得出AE=DE.根据有一组邻边相等的平行四边形是菱形即可得出结论。
20.【答案】(1)证明:如图,连接AE,CF,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵EF垂直平分AC,
∴AF=FC,AE=EC,
∴∠FAC=∠FCA,
∴∠FCA=∠ACB,
∵∠FCA+∠CFE=90°,∠ACB+∠CEF=90°,
∴∠CFE=∠CEF,
∴CE=CF,
∴AF=FC=CE=AE,
∴四边形AECF是菱形;
(2)解:∵四边形AECF是菱形,AF=5,
∴CE=AF=AE=5,
由∠B=90°,
∴在Rt△ABE中,
AB= .
∵BC=BE+EC=8,
【解析】【分析】(1)根据四边相等的四边形是菱形即可判断;(2)在Rt△ABE中,利用勾股定理可求得AB的长,在Rt△ABC中,利用勾股定理解答即可.
21.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠BCA,
∵∠BAC=∠DAC,
∴∠BAC=∠BCA,
∴AB=BC;
(2)解:连接BD交AC于O,如图所示:
∵四边形ABCD是平行四边形,AB=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,OA=OC= AC=2 ,OB=OD= BD,
∴OB= ═2,
∴BD=2OB=4,
∴平行四边形ABCD的面积= AC BD= ×
【解析】【分析】(1)根据平行四边形的性质得出AD∥BC,根据平行线的性质得出∠DAC=∠BCA,求出∠BAC=∠BCA即可;(2)求出四边形ABCD是菱形,根据勾股定理求出BO,求出BD,根据面积公式求出即可.
22.【答案】(1)①证明:∵菱形ABCD,
∴AB=BC,
∴∠BAC=∠BCA,
∵矩形EFGH,
∴FG∥EH,
∴∠EGA=∠BCA,
∴∠BAC=∠EGA,即∠FAG=∠EGA,
∴FA=FG;
②解:如图1,连接BG,
∵FG∥BC,G为AC中点,
∴FG为△ABC中位线,
∴F为AB的中点,
∵G为AC中点,BA=BC,
∴BG⊥AC,即∠BGA=90°,
∴FG=BF.
(2)解:如图2,点E在BC上运动,过点E作边BC的垂线EF交AD于点F,交AC于点O,在EF的右侧作矩形EFGH,再过点A作AM⊥BC于点M,
∵S菱形ABCD=60,AB=10
∴S△ABC=30,BC=10,
∴AM=6,
∴BM==8,
∴MC=2,
∵矩形EFGH,
∵AF∥EC,AM⊥ME,
∴四边形AMEF为矩形,
∴AF=ME,AF∥ME,
又∵∠AOF=∠COE,OA=OC,
∴△AOF≌△COE(AAS),
∴AF=EC,
∴ME=EC=1,
∴AF=1,
又∵EF=FG,EF=AM=6,
∴AG=AF+FG=1+6=7.
【解析】【分析】(1)①由菱形性质推出∠BAC=∠BCA,由矩形性质推出∠EGA=∠BCA,即得∠BAC=∠EGA,从而得∠FAG=∠EGA,进而推出FA=FG;②如图1,连接BG,易得FG为△ABC中位线,即得F为AB的中点,再由等腰三角形三线合一可得BG⊥AC,即∠BGA=90°,再由直角三角形斜边上中线等于斜边一半即可推出FG=BF;
(2)如图2,点E在BC上运动,过点E作边BC的垂线EF交AD于点F,交AC于点O,在EF的右侧作矩形EFGH,再过点A作AM⊥BC于点M,由菱形性质推出S△ABC=30,BC=10,由三角形面积公式可计算出AM=6,由勾股定理求得BM=8,从而得MC=2,由矩形AMEF性质,易推出四边形AMEF为矩形,则AF=ME,AF∥ME,又∠AOF=∠COE,OA=OC,可推出△AOF≌△COE,即得AF=EC,求得AF=1,再根据EF=FG,EF=AM=6,代入AG=AF+FG中,即可求出AG的长.
23.【答案】(1)解:如图1,过点 作 , ,垂足分别为点 、 .
四边形 为正方形,
, .
.
四边形 为正方形.
,
∵ ,
,
即 .
在 和 中,
.
.
(2)解:如图2,过点 作 ,垂足为点 ,
当 时, ,
在 中,设 ,则 , .
在 中, , .
,
.
.
(3)解:(一)当点 在 延长线上时,
因为 ,
所以只有 .
如图3,同理可证: ,
.
,
.
.
(二)当点 在射线 上时,
①如图4, ,
,
,
.
② .
,
,
此时,点 和点 重合,舍去.
③如图5, .同理可证: ,
.
.
综上所述, 的长为 , 或 .
【解析】【分析】(1)先求出 , 再证明三角形全等求解即可;
(2)利用勾股定理和三角形的面积公式计算求解即可;
(3)分类讨论,结合图形,利用全等三角形的性质求解即可。
24.【答案】(1)证明:四边形是正方形,
,,
,,
,
又,
,
(2)证明:如图,延长交于点,
,
,
,
,
,
四边形是矩形,
又,
矩形是正方形,
;
(3)证明:.理由如下:
如图,过点作交于,
,
,
,
,
,
,
又,,
,
,
,,
四边形是正方形,四边形为平行四边形,
,
又,
,
,
,
.
【解析】【分析】⑴、论证两角相等,结合图形考虑证明两角所在三角形全等。由四边形ABCD是正方形可知AB=CB,∠ABC=90°,又BG⊥BE,所以∠EBG=90°,利用同角的余角相等可得∠ABE=∠CBG,又BG=BE,由边角边论证三角形ABE和三角形CBG全等,由全等三角形性质可得结论。
⑵、由图知EF和BE同属于同一个四边形的两边,所以考虑证明四边形BEFG是正方形或菱形,由题易知四边形有三个角是直角,且有一组邻边相等,易证四边形BEFG是正方形,所以EF=EB成立。
⑶、猜想DE=CD,所以论证DE等于正方形ABCD的边长即可。通过添加辅助线DK⊥AE,和连接EC、BF,论证△DAK≌△ABE≌△CBG;又四边形CEBF是平行四边形,可得CF=BE,可论证DK=AE,∠DKE=∠AEB,KE=EB,所以△DKE≌△AEB,利用全等三角形性质得DE=AB,又AB=CD,等量代换即可得结论。
1 / 1
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
