第六章 特殊平行四边形

第六章 特殊平行四边形
一、选择题（每小题3分，共30分）
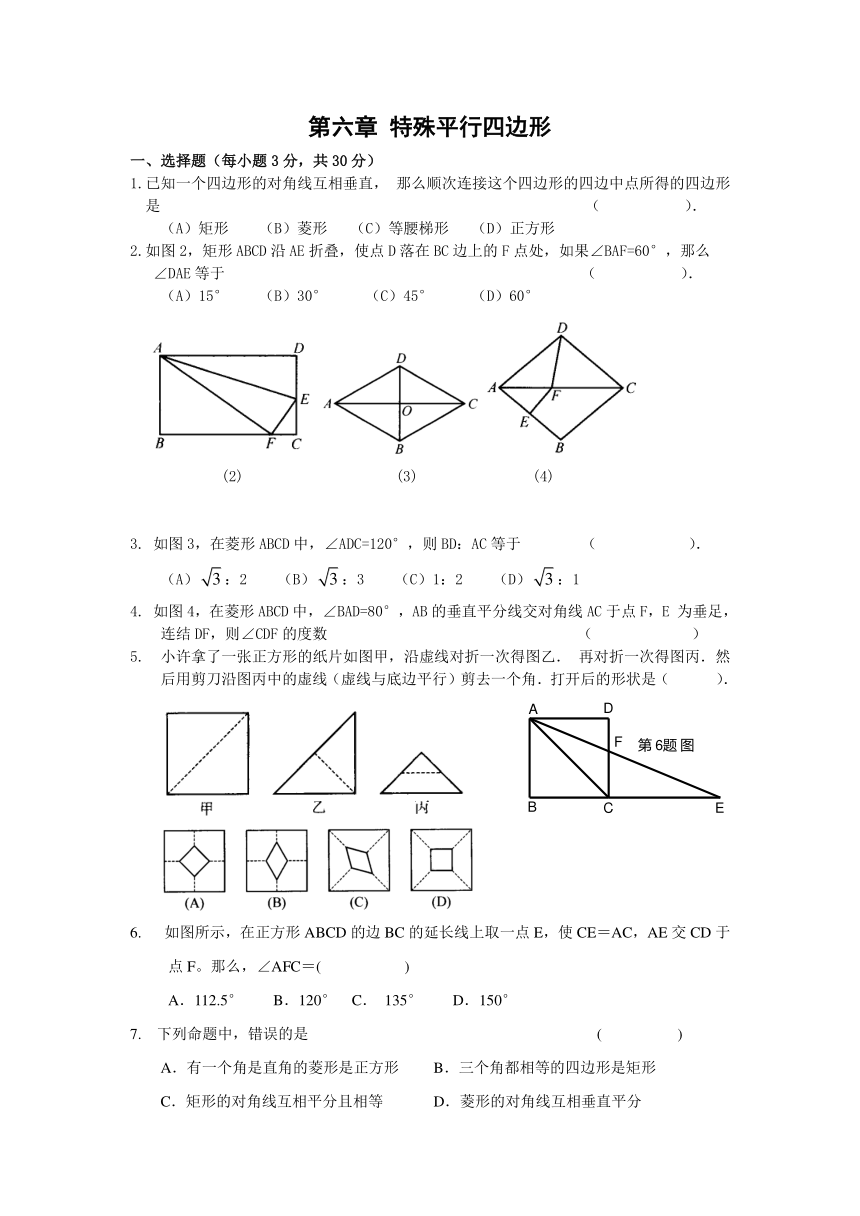
1.已知一个四边形的对角线互相垂直，那么顺次连接这个四边形的四边中点所得的四边形是 （ ）．
（A）矩形 （B）菱形 （C）等腰梯形 （D）正方形
2.如图2，矩形ABCD沿AE折叠，使点D落在BC边上的F点处，如果∠BAF=60°，那么
∠DAE等于 （ ）．
（A）15° （B）30° （C）45° （D）60°
(2) (3) (4)
3. 如图3，在菱形ABCD中，∠ADC=120°，则BD：AC等于 （ ）．
（A）：2 （B）：3 （C）1：2 （D）：1
4. 如图4，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，E为垂足， 连结DF，则∠CDF的度数 （ ）
5. 小许拿了一张正方形的纸片如图甲，沿虚线对折一次得图乙．再对折一次得图丙．然后用剪刀沿图丙中的虚线（虚线与底边平行）剪去一个角．打开后的形状是（ ）．
6. 如图所示，在正方形ABCD的边BC的延长线上取一点E，使CE＝AC，AE交CD于点F。那么，∠AFC＝( )
A．112.5° B．120° C． 135° D．150°
7. 下列命题中，错误的是 ( )
A．有一个角是直角的菱形是正方形 B．三个角都相等的四边形是矩形
C．矩形的对角线互相平分且相等 D．菱形的对角线互相垂直平分
8. 如图所示，矩形ABCD的对角线AC、BD相交于点O，如果△ABC的周长比△AOB的周长长10厘米，则矩形边AD的长是( )
A．5厘米 B．10厘米 C．7.5厘米 D．不能确定
（第10题）
9. 菱形相邻两角的比为1∶2，那么菱形的对角线与边长的比为( )
A．1∶2∶3 B．1∶2∶1 C．1∶∶2 D．1∶∶1
10. 如图，EF过矩形ABCD对角线交点O，且分别交AB、CD于点E、F，那么阴影部分的面积是矩形ABCD面积的 ( )
A． B． C． D．
二、填空题（每小题4分，共32分）
11. 在ABCD中，若添加一个条件________，则四边形ABCD是矩形；若添加一个条件_______，则四边形ABCD是菱形．
12. 已知矩形的对角线长为4cm，一条边长为2cm，则面积为________．
13. 菱形的两条对角线分别是6cm，8cm，则菱形的边长为_____，面积为______．
14. 现有一张长53cm，宽28cm的矩形纸片，要从中剪出长15cm，宽12cm的矩形小纸片，则最多能剪出______张．
15. 已知一直角三角形的两边长恰为方程x2－7x＋12＝0的两根，则此直角三角形斜边上的中线长是_______。
16 如图是某广告公司为某种商品设计的商标图案，图中阴影部分为红色．若每个小长方形的面积都是1，则红色的面积是_______。
17. 如图，已知方格纸中是4个相同的正方形，则∠1＋∠2＋∠3＝________。
18. 如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，则正方形A、B、C、D的面积的和是_______cm2。
(第18题)
三、解答题
19.（8分）已知：如图，在正方形ABCD中，AE⊥BF，垂足为P，AE与CD交于点E，BF与AD交于点F，求证：AE=BF．
20．如图，在菱形ABCD中，CE⊥AB交AB延长线于点E，CF⊥AD交AD延长线于点F，请你猜想CE和CF的大小关系，并证明你的猜想。
21. 根据要求拟编一道新题．
已知：如图所示，在矩形ABCD所在平面有一点P，且PA＝PD，请说明：PB＝PC．
请你将上述条件中的“矩形ABCD”改为另一种四边形，其余条件不变，使结论“PB＝PC”仍然成立，再根据改编后的题目画出图形，并说明理由．
22.把一个等腰直角三角形ABC沿斜边上的高线CD(裁剪线)剪一刀，从这个三角形中裁下一部分，与剩下部分能拼成一个平行四边形A'BCD(如图1)．
以下探究过程中有画图要求的，工具不限，不必写画法和证明．
探究一：
(1)想一想——判断四边形A'BCD是平行四边形的依据是__________；
(2)做一做——按上述的裁剪方法，请你拼一个与图1位置或形状不同的平行四边形，并在图2中画出示意图．
探究二：在等腰直角三角形ABC中，请你找出其它的剪裁线，把分割成的两部分拼出不同类型的特殊四边形．
(1)试一试——你能拼得所有不同类型的特殊四边形有_________，它们的裁剪线分别是_________．
(2)画一画——请在图3中画出一个你拼得的特殊四边形示意图。
www.1230.org ( http: / / www.1230.org ) 初中数学资源网 萧山朝晖初中诗梦雪上传
23. 如图所示，有两个并排在一起的正方形ACDE和BCFG．连结AF、DB，若将△AFC绕C点顺时针旋转90°，那么△AFC与△DBC能重合吗 请说明理由。
24. 如图，在四边形ABCD中，AC＝6，BD＝8且AC⊥BD，顺次连结四边形ABCD各边中点，得到四边形A1B1C1D1；再顺次连结四边形A1B1C1D1各边中点，得到四边形A2B2C2D2……如此进行下去得到四边形AnBnCnDn。
(1)证明：四边形A1B1C1D1是矩形；
(2)写出四边形A1B1C1D1和四边形A2B2C2D2的面积；
(3)写出四边形AnBnCnDn的面积；
(4)求四边形A5B5C5D5的周长。