1.5三角形全等的判定(一)课件

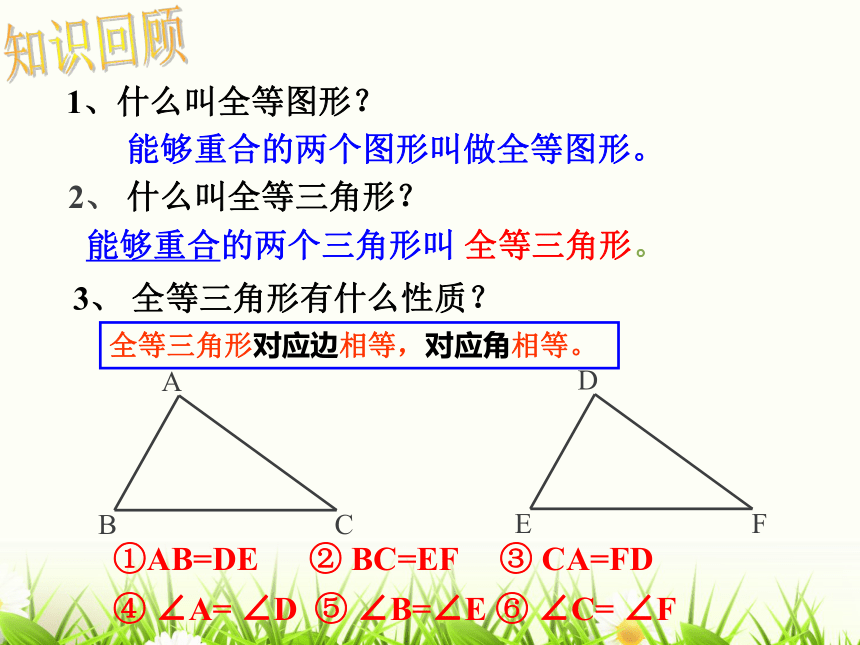
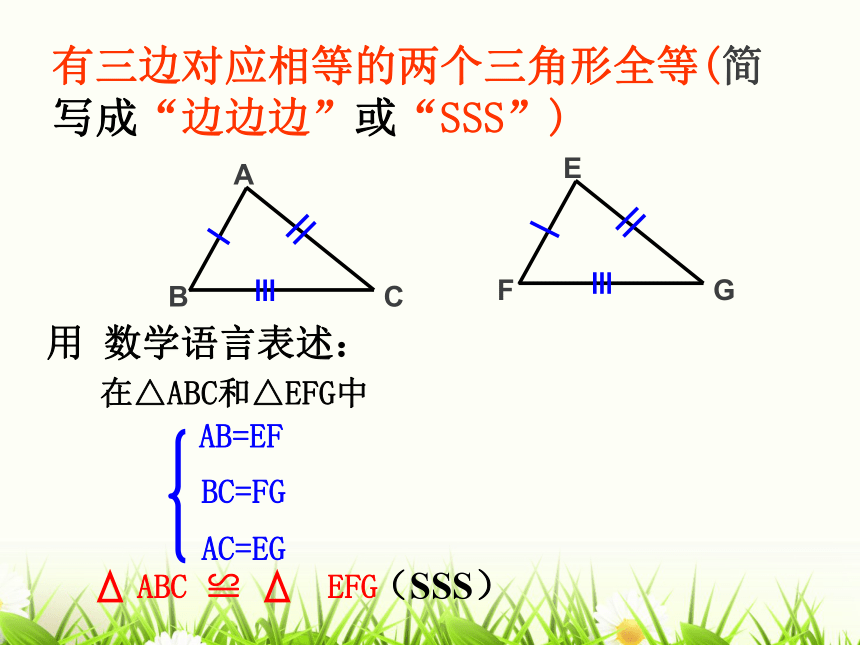
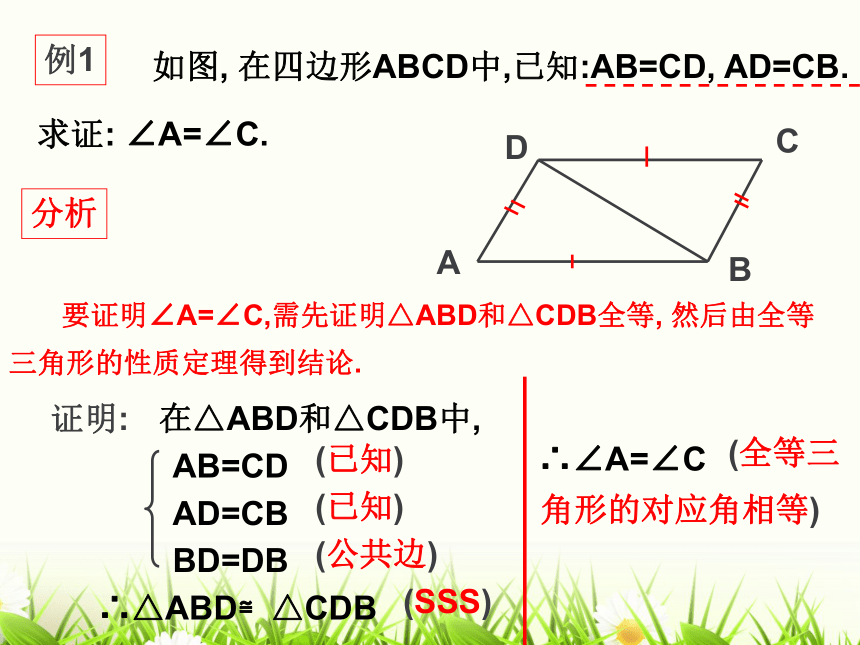
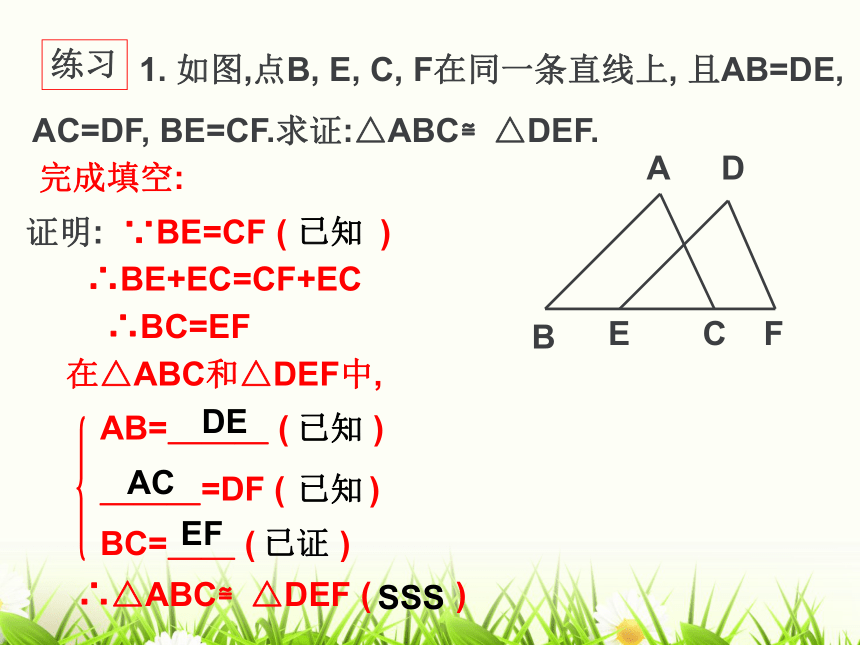
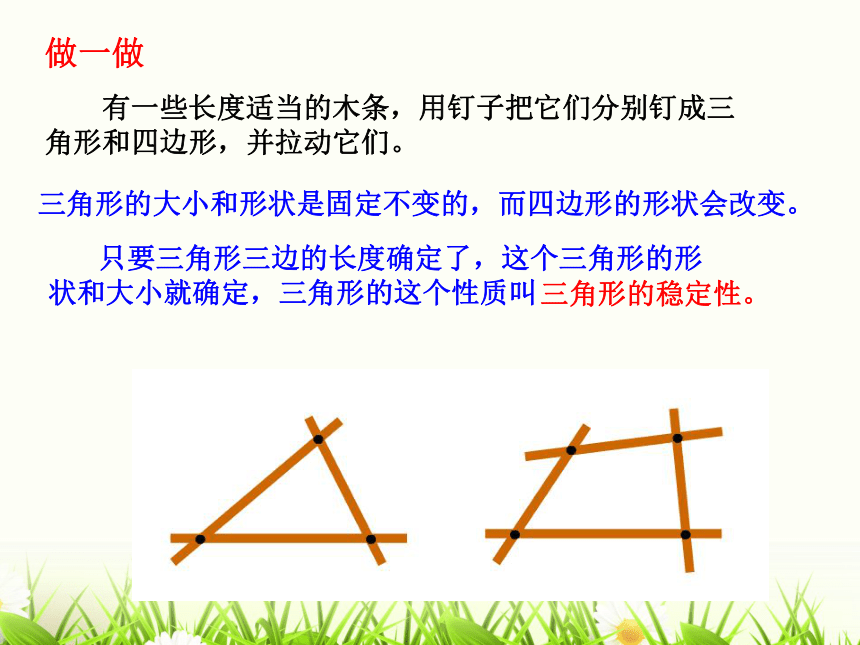
课件21张PPT。1.5 三角形全等的判定（1）知识回顾①AB=DE ② BC=EF ③ CA=FD ④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F2、 什么叫全等三角形？能够重合的两个三角形叫 全等三角形。3、 全等三角形有什么性质？1、什么叫全等图形？能够重合的两个图形叫做全等图形。全等三角形对应边相等，对应角相等。已知一个三角形的三条边分别为3cm，4cm，5cm，你能画出这个三角形吗？合作学习画法：1、画线段AB=3cm；2、分别以A、B为圆心，4cm和5cm长为半径画两条圆弧，交于点C；3、连结AC、BC；△ABC就是所求的三角形。把所画的三角形与其他同学比一比，发现了什么？有三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)例1如图, 在四边形ABCD中,已知:AB=CD, AD=CB.求证: ∠A=∠C.ABCD分析证明:在△ABD和△CDB中,AB=CD AD=CBBD=DB∴△ABD≌△CDB(已知)(已知)(公共边)(SSS)∴∠A=∠C练习1. 如图,点B, E, C, F在同一条直线上, 且AB=DE, AC=DF, BE=CF.求证:△ABC≌△DEF. ADBECF证明: ∵BE=CF ( )∴BE+EC=CF+EC∴BC=EF在△ABC和△DEF中,∴△ABC≌△DEF ( )已知已知DEACEF已知已证SSS完成填空:做一做 有一些长度适当的木条，用钉子把它们分别钉成三角形和四边形，并拉动它们。三角形的大小和形状是固定不变的，而四边形的形状会改变。 只要三角形三边的长度确定了，这个三角形的形
状和大小就确定，三角形的这个性质叫三角形的稳定性。 三角形的稳定性举例例2、 已知∠BAC，用直尺和圆规∠BAC的角平分线AD，并说明正确的理由。以上是角平分线的尺规画法作法：
1、以点A为圆心，适当的长为半径，与角的两边分别交于E、F两点。3、过点A、D作射线AD。射线AD为所求的平分线。请同学们说说理由练一练： 已知∠α，用直尺和圆规作∠ α的平分线（只要求作出图形，并保留作图痕迹）α知识运用1. 如图, 已知△ABC中,AD=AE, AB=AC=BE=CD,求证: △ABD≌△ACE.ABCDE证明: 学生自己写出过程.BE-DE=CD-DEBD=CE分析:BD=CE2. 如图, 在△ABC中,AB=AC, AD是BC边上的中线,则AD⊥BC. ABCD解:∵AD是BC边上的中线∴BD=CD在△ABD和△ACD中AB=AC ( )BD=CD ( )AD=AD ( )已知已证公共边∴△ABD≌△ACD ( )SSS∴∠ADB=∠ADC ( )全等三角形的对应角相等∵∠ADB+∠ADC=180°∴∠ADB=90°,∴AD⊥BC3. 如图, 已知AB=DE, BC=EF, AF=DC, 求证: ∠EFD=∠BCA.ABCDEF证明:∵AF=DC∴AF+FC=DC+FC在△ABC和△DEF中,AB=DE ( )BC=EF ( )AC=DF ( )∴△ABC≌△DEF ( )∴∠BCA=∠EFD ( )已知已知已证∴AC=DFSSS全等三角形的对应角相等请同学们谈谈本节课的收获与体会本节课你学到了什么？
发现了什么？
有什么收获？
还存在什么没有解决的问题？ 理解提升： 1.下列判断，其中正确的是（ ）
A．三个角对应相等的两个三角形全等
B．周长相等的两个三角形全等
C．周长相等的两个等边三角形全等
D．有两边和第三边上的高对应相等的两个三角形全等
2．如图1，已知AB=AD，如果要判定△ABC≌△ADC，则需增加条件______________．C 2．如图2，已知AB=CD，AD=BC，说出∠1=∠2的理由．
解：在_______和_______中
图1∴____________（ ）
∴∠1=∠2（ ）BC=CD △ABC △CDA AB=CD 已知 AD=BC 已知 AC=CA 公共边 △ABC≌△CDA SSS 全等三角形对应角相等 3．如图，已知△ABF≌△DEC，且AC=DF，说明△ABC≌△DEF的理由．
解：∵△ABF≌△DEC
∴AB=________ BF=________
又∵BC=BF+_________，EF=CE+________．
∴BC=_________．
在△ABC与△DEF中 ∴△ABC≌△DEF（ ）DECEFCFCEFAB=DE（已证）BC=EF（已证）AC=DF（已知）SSS4．如图，△ABC和△DBC中，AB=CD，AC=BD，AC和DB相交于O，说出∠1=∠2的理由．AB=CD(已知）AC=BD（已知）BC=CB（公共边）∴△ABC≌△DCB（SSS）∴∠ABC=∠DCB（全等三角形对应角相等）∴∠DBC=∠ACB （全等三角形对应角相等）∵∠1=∠ABC-∠DBC，∠2=∠DCB-∠ACB，∴∠1=∠2