1.5三角形全等的判定(二)课件

课件19张PPT。1.5全等三角形的判定
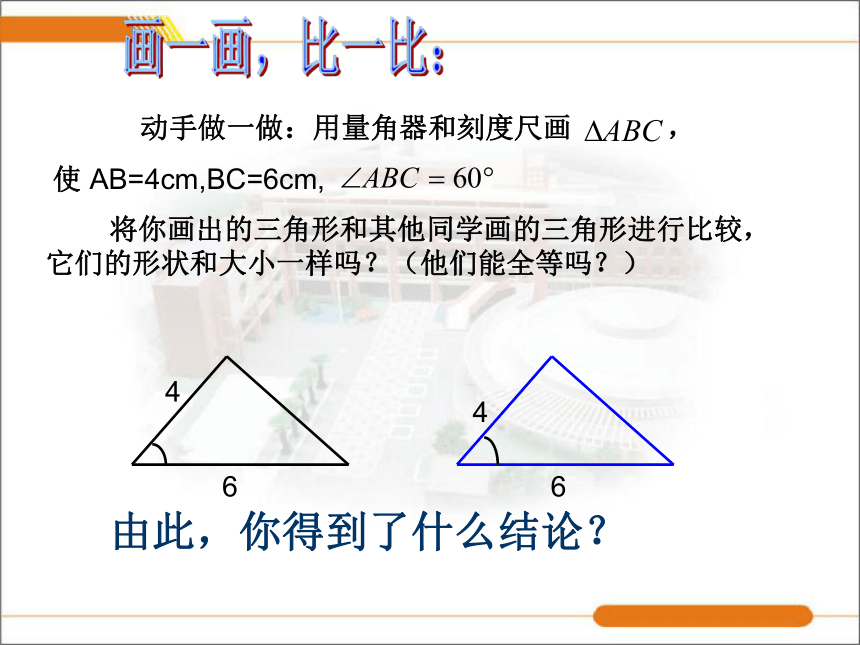
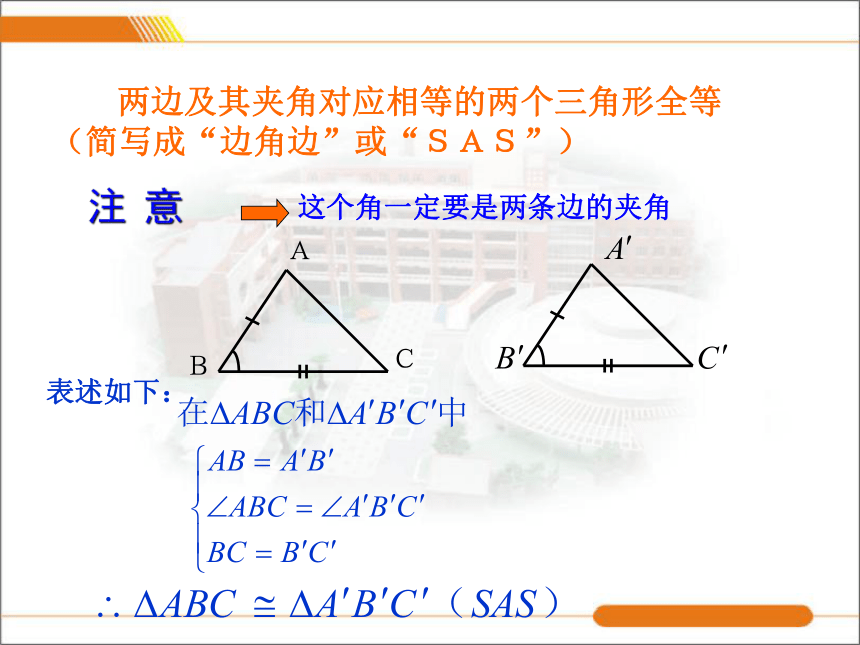
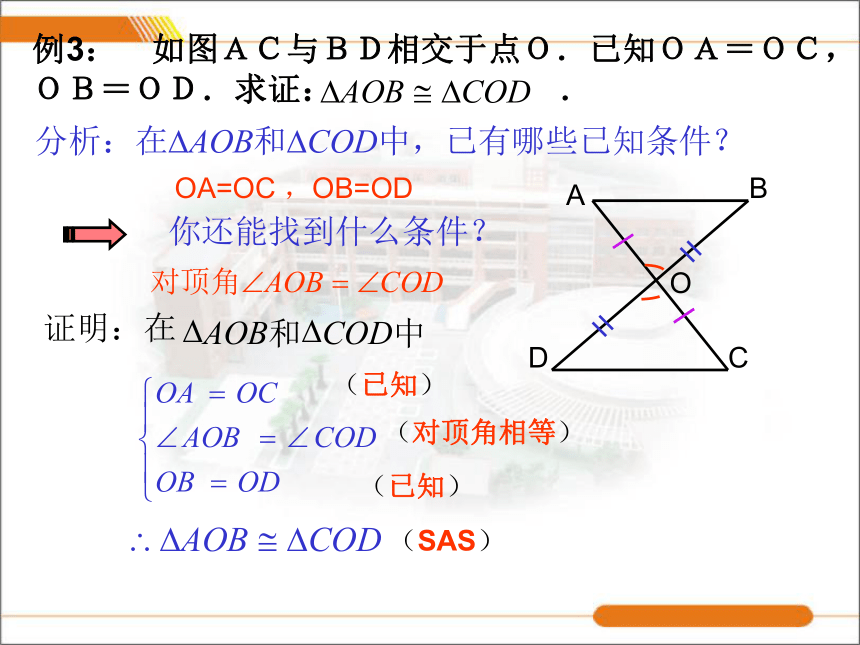
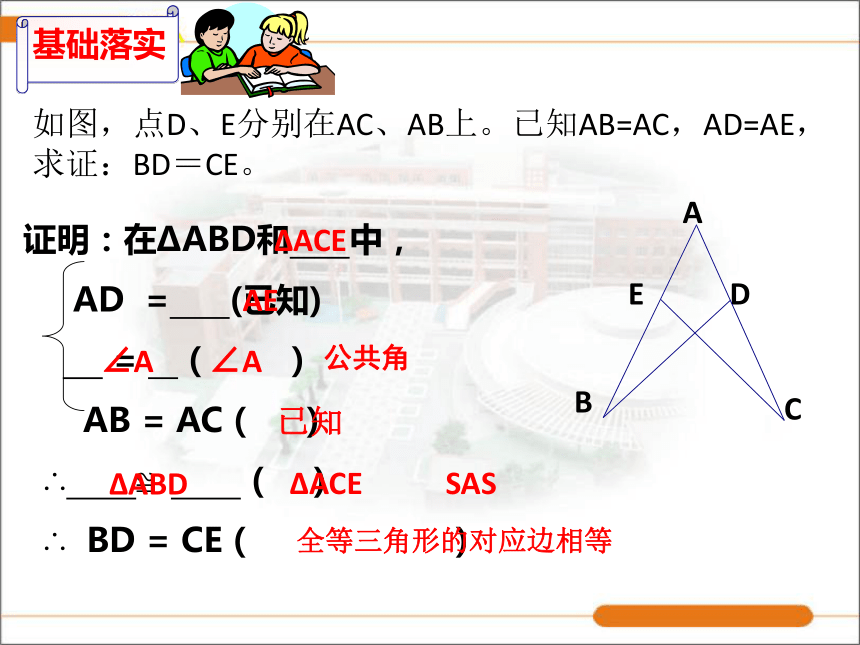
（2）画一画，比一比： 将你画出的三角形和其他同学画的三角形进行比较，它们的形状和大小一样吗？（他们能全等吗？）由此，你得到了什么结论？ 两边及其夹角对应相等的两个三角形全等（简写成“边角边”或“ＳＡＳ”）OA=OC ，OB=OD（已知）（对顶角相等）（已知）（SAS）如图，点D、E分别在AC、AB上。已知AB=AC，AD=AE，求证：BD＝CE。ΔACEAE∠A∠A已知ΔABDΔACESAS全等三角形的对应边相等公共角分析；
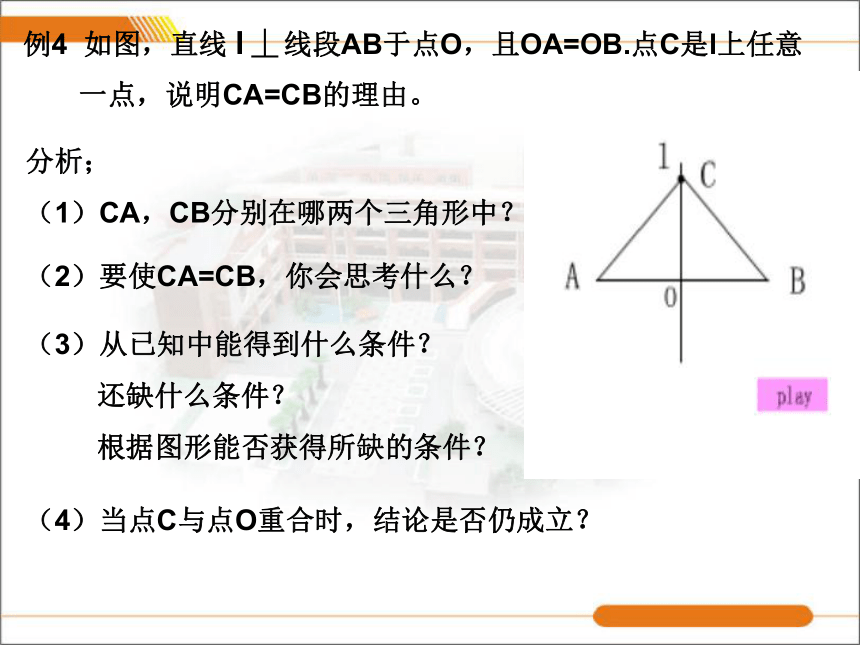
（1）CA，CB分别在哪两个三角形中？（2）要使CA=CB，你会思考什么？（3）从已知中能得到什么条件？
还缺什么条件？
根据图形能否获得所缺的条件？（4）当点C与点O重合时，结论是否仍成立？垂直平分线定义
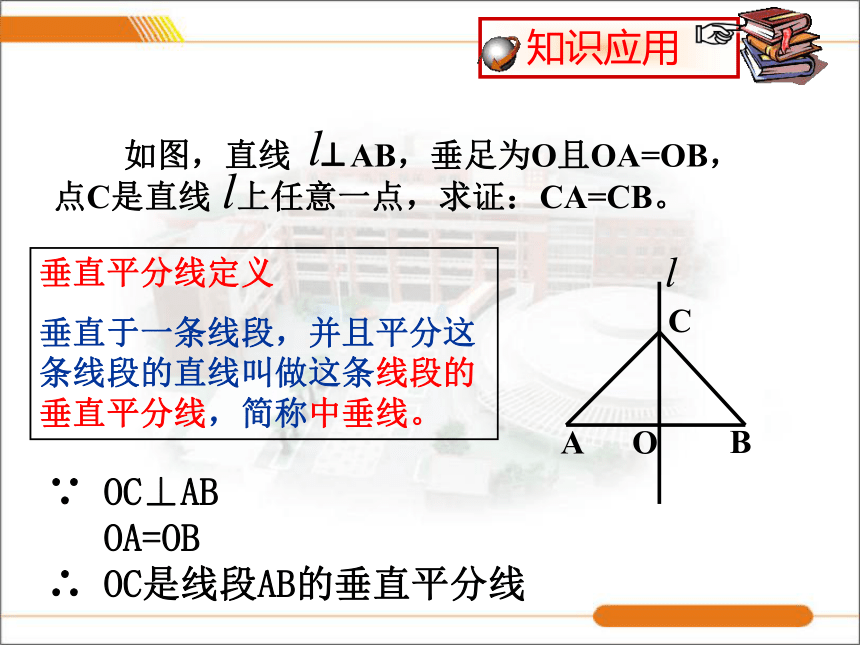
垂直于一条线段，并且平分这条线段的直线叫做这条线段的垂直平分线，简称中垂线。∵ OC⊥AB
OA=OB
∴ OC是线段AB的垂直平分线 点C是线段AB的垂直平分线上的特殊的
点，还是任意的点？由此你能得到什么结论？线段垂直平分线 上的点到线段两端的距离相等。（线段垂直平分线的性质）o( SSS )o在D ABC和D ADC和中补充练习：①. 如图(1)， △ABC中，BC=10cm，AB的中垂线交于BC于D，AC的中垂线交BC于E，则△ADE的周长是______.13cm10cm如图，已知：AB=AC，则添加什么条件可得△ABD≌ △ACD?请说明理由.拓展(1)补充∠ＢAＤ=∠ＣAＤAB=AC (已知)∠ＢAＤ=∠ＣAＤ(已知)AD=AＤ(公共边)∴ △AＢＤ≌△ACＤ（SAS）(2)补充ＢＤ＝ＣＤAB=AC (已知)AD=AＤ(公共边)∴ △AＢＤ≌△ACＤ(SSS)BD=CD(已知) 通过本堂课的学习和探索，你学会了什么?
2. 谈一谈!你对这堂课的感受?
　　　　　　　　　　　　　　　　　　　　　　在实际生活中, 我们面对不能直接测量物
体的宽度或距离时. 可以把它们转化为数学问
题,通过三角形全等,再利用对应边相等来解决!
　　　　　　　　　　　　　　　　　　忆一忆，谈一谈 在下面的图中，有①、②、③三个三角形，根据
图中条件，三角形_____和_____全等（填序号即可）①②拓展应用：3。已知，AB=AC，BD=CD，问AD所在的直线是
BC的垂直平分线吗？如果是，请写出理由。E你来说一说，这节课你学到了什么？课堂小结:2. 用尺规作图,已知一角与夹角两边的三角形3. 线段垂直平分线的概念1. 三角形全等的判定方法二,有一个角和夹这个角的两边也对应相等的两个三角形全等(边角边或SAS)4. 线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等.
1。已知B、C、E在同一条直线上，∠1= ∠2，AC=DC，
求证：AB=DB。补充练习：2。已知AB=AC，AD=AE， ∠1= ∠2，求证CE=BD。