浙教版八年级下册第四章平行四边形培优练习(含解析)
文档属性
| 名称 | 浙教版八年级下册第四章平行四边形培优练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 683.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 08:32:21 | ||
图片预览


文档简介
浙教版八年级下册第四章平行四边形培优练习
一、选择题
1.围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.如图为某对战局部棋谱,由黑白棋子摆成的图案是中心对称的是( )
A. B. C. D.
2.如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.6 B.7 C.8 D.9
3.在□ABCD中,若∠A:∠B:∠C=1:2:1,则∠D的度数为( )
A.67.5° B.90° C.112.5° D.120°
4.小明不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
A.①② B.①④ C.②③ D.③④
5.用反证法证明“四边形中至少有一个角是钝角或直角”,可假设四边形的四个角都是( )
A.钝角或直角 B.钝角 C.直角 D.锐角
6.如图,平行四边形的对角线,交于点,已知,,的周长为15,则的长为( )
A.5 B.6 C.7 D.8
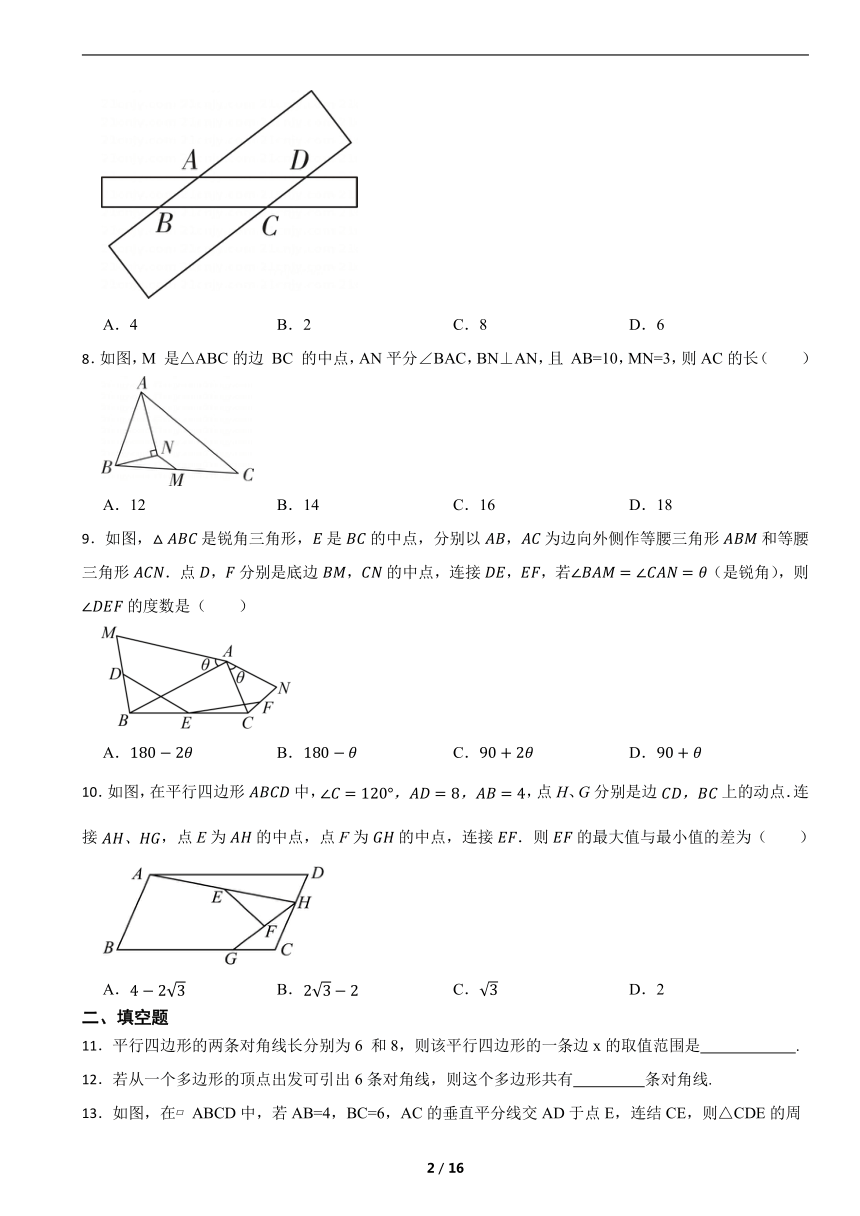
7.如图,两条宽度分别为1和2的长方形纸条交叉放置,重叠部分为四边形ABCD.若AB+BC=6,则四边形ABCD的面积为 ( )
A.4 B.2 C.8 D.6
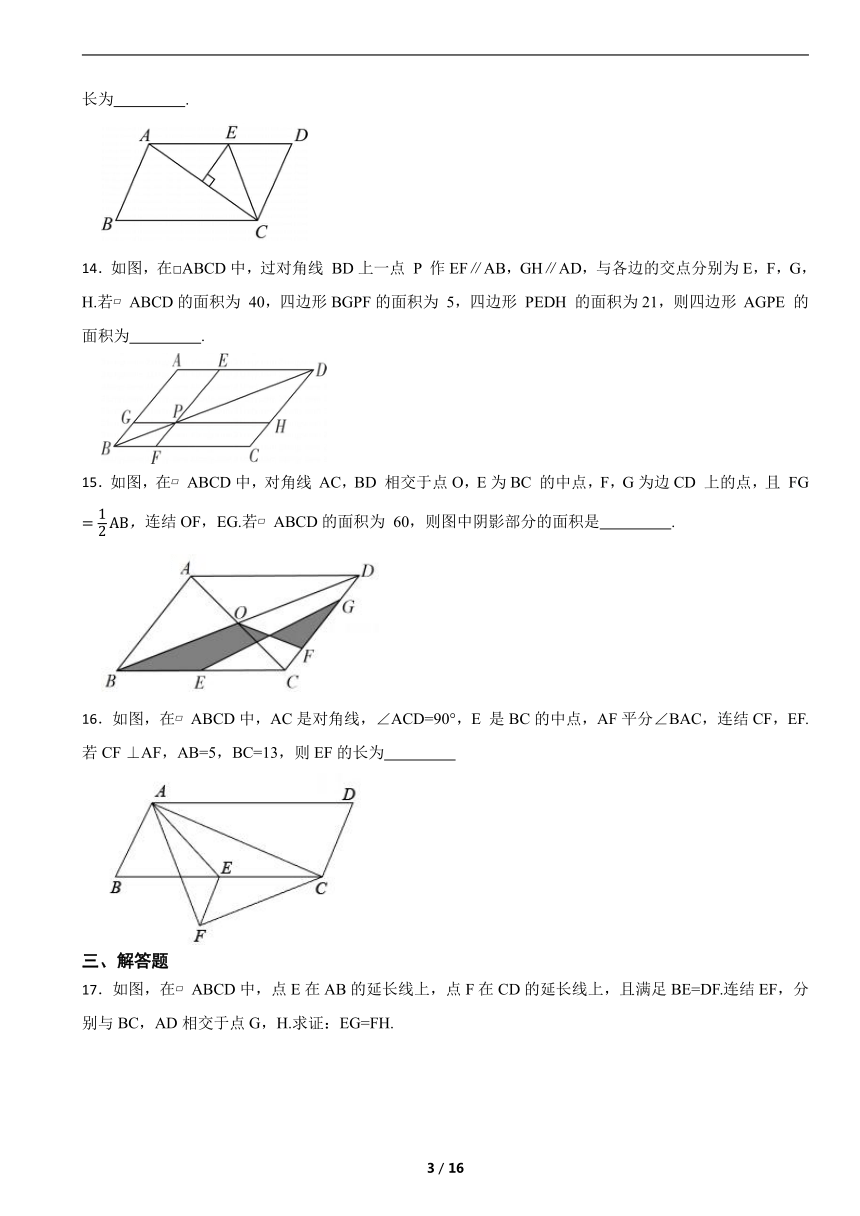
8.如图,M 是△ABC的边 BC 的中点,AN平分∠BAC,BN⊥AN,且 AB=10,MN=3,则AC的长( )
A.12 B.14 C.16 D.18
9.如图,是锐角三角形,是的中点,分别以,为边向外侧作等腰三角形和等腰三角形.点,分别是底边,的中点,连接,,若(是锐角),则的度数是( )
A. B. C. D.
10.如图,在平行四边形中,,点H、G分别是边上的动点.连接,点E为的中点,点F为的中点,连接.则的最大值与最小值的差为( )
A. B. C. D.2
二、填空题
11.平行四边形的两条对角线长分别为6 和8,则该平行四边形的一条边x的取值范围是 .
12.若从一个多边形的顶点出发可引出6条对角线,则这个多边形共有 条对角线.
13.如图,在 ABCD中,若AB=4,BC=6,AC的垂直平分线交AD于点E,连结CE,则△CDE的周长为 .
14.如图,在□ABCD中,过对角线 BD上一点 P 作EF∥AB,GH∥AD,与各边的交点分别为E,F,G,H.若 ABCD的面积为 40,四边形BGPF的面积为 5,四边形 PEDH 的面积为21,则四边形 AGPE 的面积为 .
15.如图,在 ABCD中,对角线 AC,BD 相交于点O,E为BC 的中点,F,G为边CD 上的点,且 FG 连结OF,EG.若 ABCD的面积为 60,则图中阴影部分的面积是 .
16.如图,在 ABCD中,AC是对角线,∠ACD=90°,E 是BC的中点,AF平分∠BAC,连结CF,EF.若CF ⊥AF,AB=5,BC=13,则EF的长为
三、解答题
17.如图,在 ABCD中,点E在AB的延长线上,点F在CD的延长线上,且满足BE=DF.连结EF,分别与BC,AD相交于点G,H.求证:EG=FH.
18.如图,在 Rt△ABC 中,∠BAC=90°,AD 是BC 边上的中线,E,F 分别是AB,AC的中点,连结 EF,ED,FD.求证:AD=EF.
19.如图,在ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上, 且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连结BD交AC于点O,若BD= 10,AE+CF=EF ,求EG的长.
20.如图,在ABCD中,点P是对角线AC上一动点,过点P作PM∥DC,且PM=DC,连结BM,CM,BP,PD.
(1)求证:△ADP≌△BCM;
(2)若PA=PC,设△ABP的面积为S,四边形BPCM的面积为T,求的值.
21.在 ABCD 中,∠C=45°,AD=BD,P为线段CD上的动点(点P不与点D 重合),连结 AP,过点P作EP⊥AP交直线BD 于点E.
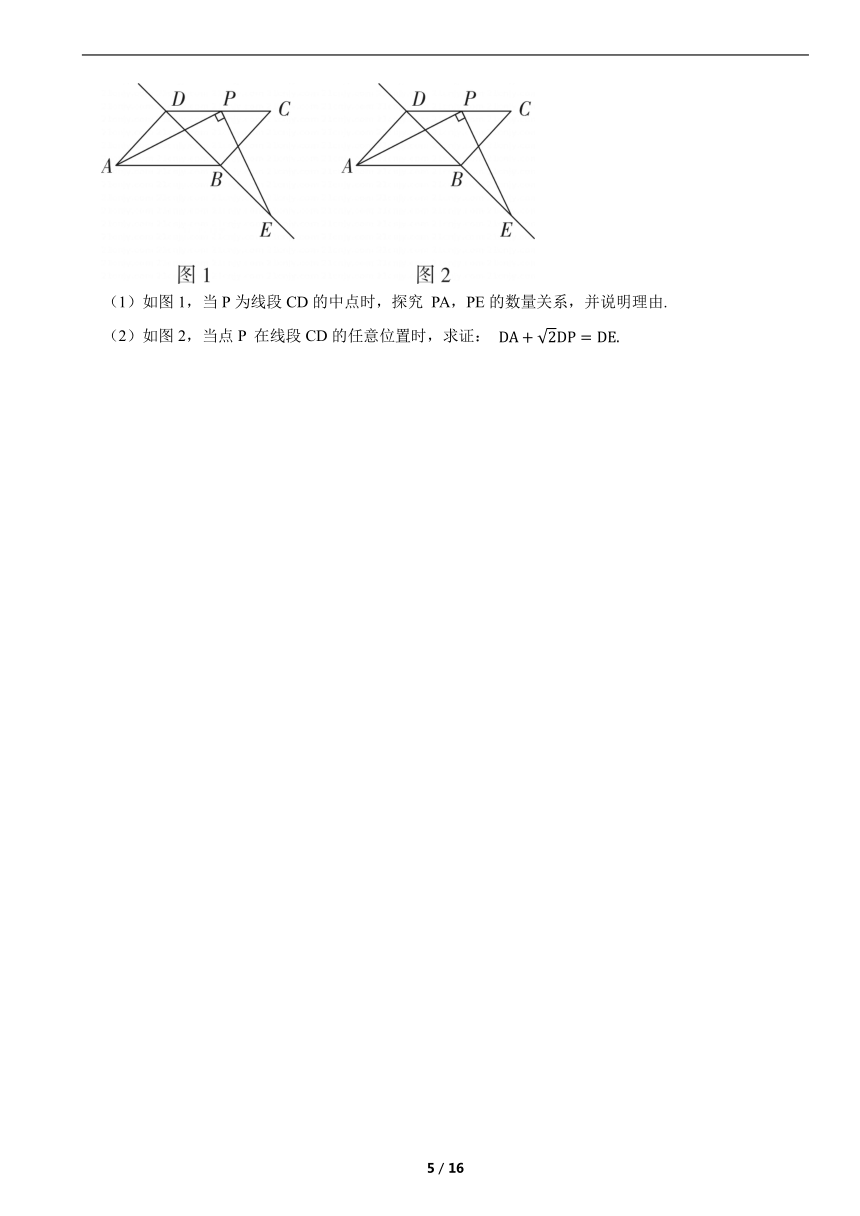
(1)如图1,当P为线段CD的中点时,探究 PA,PE的数量关系,并说明理由.
(2)如图2,当点P 在线段CD的任意位置时,求证:
答案解析部分
1.【答案】A
【解析】【解答】解:A、是中心对称图形,故符合题意;
B、不是中心对称图形,故不符合题意;
C、不是中心对称图形,故不符合题意;
D、不是中心对称图形,故不符合题意;
故答案为:A.
【分析】中心对称图形:把一个图形绕着某一点旋转180°后,旋转后的图形能够与原来的图形重合,据此判断即可.
2.【答案】C
【解析】【解答】解:由题意得:(n-2)×180°=3×360°,
解得:n=8;
故答案为:C.
【分析】根据多边形的内角和和外角和公式列式,求出n即可。
3.【答案】D
【解析】【解答】解: 在□ABCD中,∠A+∠B=180°,∠D=∠B,
∵∠A:∠B=1:2,
∴∠B=180°×=120°,
∴∠D=∠B=120°.
故答案为:D.
【分析】由平行四边形的性质可得∠A+∠B=180°,∠D=∠B,利用∠A:∠B=1:2求出∠B的度数即可.
4.【答案】C
【解析】【解答】∵ 只有②③两块碎玻璃的两边互相平行,且这两块有公共边
∴ 角的两边的延长线的交点就是平行四边形的顶点.
∴ 带②③两块玻璃就可以确定平行四边形的大小.
故答案为:C.
【分析】根据平行四边形的判定定理:两组对边分别平行的四边形是平行四边形.
四块玻璃中需要找到两边互相平行且可以连在一起的两块玻璃.
5.【答案】D
【解析】【解答】解:用反证法证明“四边形中至少有一个角是钝角或直角”,
可先假设四边形的四个角都是锐角.
故答案为:D.
【分析】利用反证法证明的第一步为:假设结论不成立,故只需找出至少有一个角是钝角或直角的反面即可.
6.【答案】C
【解析】【解答】∵平行四边形的对角线,交于点,已知,,
∴BO=DO=BD=5,CO=AO=AC=3,
∵的周长为15,
∴BC=15-(BO+CO)=15-(5+3)=7,
∴AD=BC=7,
故答案为:C.
【分析】先利用平行四边形的性质可得BO=DO=BD=5,CO=AO=AC=3,再利用三角形的周长公式求出BC的长,最后利用平行四边形的性质可得AD=BC.
7.【答案】A
【解析】【解答】解:依题意得:AB∥CD,AD∥BC,则四边形ABCD是平行四边形.
如图,过点A作AE⊥BC于点E,过点A作AF⊥CD于点F,
∴AE=1,AF=2,
∴BC AE=AB AF,
∴BC=2AB.
又∵AB+BC=6,
∴AB=2,BC=4
∴四边形ABCD的面积=2×2=4
故答案为:A.
【分析】本题考查了平行四边形的判定与性质.先作辅助线:过点A作AE⊥BC于点E,过点A作AF⊥CD于点F,平行四边形ABCD的面积可表示为:BC AE=AB AF,可推出:BC=2AB.进而得出AB与BC的数量关系:BC=2AB,结合AB+BC=6,可求AB和BC,即可求出平行四边形的面积.
8.【答案】C
【解析】【解答】解:延长线段BN交AC于E,
∵AN平分∠BAC,
∴∠BAN=∠EAN,
在△ABN和△AEN中
∴△ABN≌△AEN(ASA)
∴AE=AB=10,BN=EN,
而M是BC边的中点,
∴CE=2MN=2×3=6,
∴AC=AE+CE=10+6=16.
故答案为:C.
【分析】延长线段BN交AC于E,由角平分线定义可得∠BAN=∠EAN,结合已知用角边角可证△ABN≌△AEN,则AE=AB=10,BN=EN,由三角形中位线定理得CE=2MN求出CE的值,然后根据线段的构成AC=AE+CE可求解.
9.【答案】B
【解析】【解答】解:如图,连接、,
、是等腰三角形,
,,
,
,
,
,
,
,
点是的中点,点,分别是底边,的中点,
,,
,,
,
,
,
故答案为:B.
【分析】先利用等腰三角形的性质通过SAS证得,再通过三角形的内角和定理得到相等,然后利用中位线定理和外角的定义得到的和,进而求得的度数.
10.【答案】C
【解析】【解答】解:如下图所示:取AD的中点M,连接CM,AG,AC,过点A作AN⊥BC,
∵四边形ABCD是平行四边形,∠BCD=120°,AB=4,
∴∠D= 180°-∠BCD=60°,AB= CD=4,
∴AM=DM=DC=4,
∴△CDM是等边三角形,
∴∠DMC=∠MCD=60°,CM=AM,
∴∠MAC= ∠MCA=30°,
∴∠ACD =∠MCA+∠MCD= 90°,
∴,
∵∠ACN=∠DAC=30°,
∴,
∵AE = EH,GF = FH,
∴
∴EF的最大值与最小值的差为,
故答案为:C.
【分析】根据平行四边形的性质求出∠D= 180°-∠BCD=60°,AB= CD=4,再求出△CDM是等边三角形,最后利用勾股定理和直角三角形30°角的性质等计算求解即可。
11.【答案】1<x<7
【解析】【解答】解:如图,
∵四边形ABCD是平行四边形,对角线AC与BD相交于点O,且AC=6,BD=8,
∴OB=BD=4,OC=AC=3,
∴4-3<BC<4+3,
即1<BC<7,
∴ 该平行四边形的一条边x的取值范围1<x<7.
故答案为:1<x<7.
【分析】画出示意图,由平行四边形的对角线互相平分得OB=BD=4,OC=AC=3,进而根据三角形三边关系,任意两边之和大于第三边,任意两边之差小于第三边可得x的取值范围.
12.【答案】27
【解析】【解答】解:由题意得多边形边数为6+3=9,
∴ 这个多边形的对角线共有×9×(9-3)=27.
故答案为:27.
【分析】n边形从一个顶点出发可引出(n-3)条对角线,对角线的条数共有n(n-3)条,据此解答即可.
13.【答案】10
【解析】【解答】∵AC的垂直平分线交AD于点E,
∴EA=EC,
∵四边形ABCD是平行四边形,
∴CD=AB=4,AD=BC=6,
∴△CDE的周长=CD+EC+DE=CD+EA+DE=CD+AD=4+6=10.
故答案为:10.
【分析】由线段的垂直平分线的性质可得EA=EC,根据平行四边形的性质得CD=AB,AD=BC,然后根据三角形的周长等于三角形的三边之和可求解.
14.【答案】7
15.【答案】15
【解析】【解答】解:连接OE,如下图:
∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD,O为BD的中点,
∵点O、E分别是BD和BC的中点
∴OE∥CD且OE=CD=AB
∴∠EOF=∠GFO,∠OEG=∠EGF
∵FG=AB
∴OE=FG
∵∠EOF=∠GFO,OE=FG,∠OEG=∠EGF
∴△OEH≌△FGH(ASA)
∴OH=HF
∵S ABCD=BC×=AB×=60
∴S△BOE=×BE×=××BC×=×60=,
S△EOH=S△GFH=×OE×=×AB×=×60=;
∴S阴影部分=+2×=15
故答案为:15.
【分析】根据平行四边形的性质,可得AB=CD,AB∥CD;根据三角形的中点性质,可得OE∥CD且OE=CD;根据三角形全等的判定(ASA)和性质,可得OH=HF;根据平行四边形的面积公式和三角形的面积公式,即可求出阴影部分的面积.
16.【答案】
【解析】【解答】解:延长CF和AB,交于点H,如下图:
∵四边形ABCD是平行四边形
∴AB∥CD,
∴∠ACD=∠BAC=90°
∴AC=
∵AF平分∠BAC,且CF⊥AF
∴AH=AC=12,FH=FC
∵AB=5
∴BH=12-5=7
∵点E是BC的中点,FH=FC
∴EF=BH=
故答案为:.
【分析】根据平行四边形的性质,可得∠ACD=∠BAC;根据勾股定理,可得AC的长;根据等腰三角形三线合一的性质,可得AH=HC;根据三角形中线的性质,可得EF的长.
17.【答案】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∠ABC=∠CDA,
∴∠E=∠F,∠EBG=∠FDH,
∵ BE=DF ,
∴△EBG≌△FDH(ASA),
∴EG=FH.
【解析】【分析】利用性行四边形的性质可得AB∥CD,∠ABC=∠CDA,从而推出∠E=∠F,∠EBG=∠FDH,再用ASA证△EBG≌△FDH,利用全等三角形的性质即可得解.
18.【答案】证明:∵ ∠BAC=90°,AD是BC边上的中线,
∴ AD=BC,
∵ E,F分别是AB,AC的中点,
∴ EF=BC,
∴ AD=EF.
【解析】【分析】根据直角三角形的斜边中线等于斜边的一半可得AD=BC,根据三角形的中位线等于第三边的一半得EF=BC,即可求得.
19.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠GAE=∠HCF.
∵点G,H分别是AB ,CD的中点,AB= CD,∴AG=CH.∵AE=CF,
∴△AGE≌△CHF ( SAS),∴GE= HF, ∠AEG= ∠CFH,∴∠GEF =∠HFE,∴GE∥HF.又∵GE=HF,∴四边形EGFH是平行四边形.
(2)解:连结BD交AC于点O,如图.
∵四边形ABCD是平行四边形,
∴OA = OC, OB=0D. BD= 10,
∴ OB=OD=5.∵AE= CF ,OA=OC,
∴ OE=OF.∵AE+CF= EF,
∴2AE= EF=20E,∴AE=OE.又∵点G是AB的中点,∴EG是△ABO
的中位线,∴EG=OB=2.5,∴EG的长为2.5.
【解析】【分析】(1)根据平行四边形的性质可证出△AGE≌△CHF ( SAS),再根据全等三角形的性质可得出GF=HF且GF∥HF,从而证出四边形EGFH是平行四边形;
(2)根据平行四边形的性质和已知 AE+CF=EF ,可知E是OA的中点,所以EG是△ABO的中位线,根据中位线的性质可求出EG的长度.
20.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AD= BC,∠ADC+ ∠BCD =180°.∵PM∥ DC,且PM=DC,∴四边形PMCD是平行四边形,
∴PD=CM,∠PDC+∠DCM= 180°,∴∠ADP= ∠ BCM.在△ADP和△BCM中,,∴△ADP≌△BCM( SAS). .
(2)解:如图,作BH⊥AC于点H,DG⊥AC于点G,∵四边形ABCD是平行四边形,△ABC≌△CDA,∴BH= DG,
∴,即S△BCP = 2S△ABP,,即S△ADP=S△ABP.
∵△ADP≌△BCM,∴S△ADP=S△BCM,∴
【解析】【分析】(1)根据已知条件可知四边形PMCD是平行四边形,则根据平行四边形的性质可证△ADP≌△BCM;
(2)根据四边形ABCD是平行四边形,可知△ABC≌△CDA,从而得到同底边上的高BH= DG,得到S△BCP= 2S△ABP,而△ABP和△ADP是同底等高,所以面积相等,四边形BPCM的面积=△BCP的面积+△ACM的面积,而根据(1)可知△ACM的面积=△ADP的面积,从而可得出答案.
21.【答案】(1)解:PA=PE,理由如下:
连接PB,如下图:
∵四边形ABCD是平行四边形
∴AD=BC,∠ADC=180°-45°=135°
∵AD=BD
∴BD=BC
∵∠C=45°
∴三角形DBC是等腰直角三角形
∴∠BDC=45°,∠DBP=45°
∴∠PBE=∠ADC=135°
∵P是DC的中点
∴BP⊥DC,DP=BP
∴∠DPA+∠APB=∠APB+∠BPE=90°
∴∠DPA=∠BPE
∵∠DPA=∠BPE,DP=BP,∠PBE=∠ADC
∴△DPA≌△BPE(ASA)
∴PA=PE;
(2)证明:过点P作PF垂直CD交DE于点F,如下图:
∵PF⊥CD,EP⊥AP
∴∠DPE=∠APE=90°
∴∠DPA+∠APB=∠APB+∠FPE
∴∠DPA=∠FPE
∵四边形ABCD是平行四边形
∴∠C=∠DAB=45°,AB∥CD
∵AD=BD
∴∠DAB=∠DBA=45°
∴∠ADB=∠DBC=90°
∴∠PFD=45°
∴∠PFD=∠PDF
∴PD=PF
∴∠PDA=∠PFE=135°
∴△DPA≌△FPE((ASA)
∴AD=EF
∴DF=DP=DP
∵DE=DF+EF
∴DA+DP=DE;
【解析】【分析】(1)根据平行四边形的性质和等量代换原则可得BD=BC;根据等腰直角三角形的判定和性质可得∠BDC=45°,∠DBP=45°;根据三角形全等的判定(ASA)和性质可得PA=PE;
(2)根据等量代换原则可得∠DPA=∠FPE根据平行四边形的性质可得∠C=∠DAB=45°,AB∥CD;根据等腰直角三角形的性质和等量代换原则可得∠PFD=45°,∠PDA=∠PFE=135°;根据三角形全等的判定(ASA)和性质可得AD=EF;根据特殊角的三角函数的应用可得DF=DP,根据等量代换原则即可解题.
1 / 1
一、选择题
1.围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.如图为某对战局部棋谱,由黑白棋子摆成的图案是中心对称的是( )
A. B. C. D.
2.如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.6 B.7 C.8 D.9
3.在□ABCD中,若∠A:∠B:∠C=1:2:1,则∠D的度数为( )
A.67.5° B.90° C.112.5° D.120°
4.小明不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
A.①② B.①④ C.②③ D.③④
5.用反证法证明“四边形中至少有一个角是钝角或直角”,可假设四边形的四个角都是( )
A.钝角或直角 B.钝角 C.直角 D.锐角
6.如图,平行四边形的对角线,交于点,已知,,的周长为15,则的长为( )
A.5 B.6 C.7 D.8
7.如图,两条宽度分别为1和2的长方形纸条交叉放置,重叠部分为四边形ABCD.若AB+BC=6,则四边形ABCD的面积为 ( )
A.4 B.2 C.8 D.6
8.如图,M 是△ABC的边 BC 的中点,AN平分∠BAC,BN⊥AN,且 AB=10,MN=3,则AC的长( )
A.12 B.14 C.16 D.18
9.如图,是锐角三角形,是的中点,分别以,为边向外侧作等腰三角形和等腰三角形.点,分别是底边,的中点,连接,,若(是锐角),则的度数是( )
A. B. C. D.
10.如图,在平行四边形中,,点H、G分别是边上的动点.连接,点E为的中点,点F为的中点,连接.则的最大值与最小值的差为( )
A. B. C. D.2
二、填空题
11.平行四边形的两条对角线长分别为6 和8,则该平行四边形的一条边x的取值范围是 .
12.若从一个多边形的顶点出发可引出6条对角线,则这个多边形共有 条对角线.
13.如图,在 ABCD中,若AB=4,BC=6,AC的垂直平分线交AD于点E,连结CE,则△CDE的周长为 .
14.如图,在□ABCD中,过对角线 BD上一点 P 作EF∥AB,GH∥AD,与各边的交点分别为E,F,G,H.若 ABCD的面积为 40,四边形BGPF的面积为 5,四边形 PEDH 的面积为21,则四边形 AGPE 的面积为 .
15.如图,在 ABCD中,对角线 AC,BD 相交于点O,E为BC 的中点,F,G为边CD 上的点,且 FG 连结OF,EG.若 ABCD的面积为 60,则图中阴影部分的面积是 .
16.如图,在 ABCD中,AC是对角线,∠ACD=90°,E 是BC的中点,AF平分∠BAC,连结CF,EF.若CF ⊥AF,AB=5,BC=13,则EF的长为
三、解答题
17.如图,在 ABCD中,点E在AB的延长线上,点F在CD的延长线上,且满足BE=DF.连结EF,分别与BC,AD相交于点G,H.求证:EG=FH.
18.如图,在 Rt△ABC 中,∠BAC=90°,AD 是BC 边上的中线,E,F 分别是AB,AC的中点,连结 EF,ED,FD.求证:AD=EF.
19.如图,在ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上, 且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连结BD交AC于点O,若BD= 10,AE+CF=EF ,求EG的长.
20.如图,在ABCD中,点P是对角线AC上一动点,过点P作PM∥DC,且PM=DC,连结BM,CM,BP,PD.
(1)求证:△ADP≌△BCM;
(2)若PA=PC,设△ABP的面积为S,四边形BPCM的面积为T,求的值.
21.在 ABCD 中,∠C=45°,AD=BD,P为线段CD上的动点(点P不与点D 重合),连结 AP,过点P作EP⊥AP交直线BD 于点E.
(1)如图1,当P为线段CD的中点时,探究 PA,PE的数量关系,并说明理由.
(2)如图2,当点P 在线段CD的任意位置时,求证:
答案解析部分
1.【答案】A
【解析】【解答】解:A、是中心对称图形,故符合题意;
B、不是中心对称图形,故不符合题意;
C、不是中心对称图形,故不符合题意;
D、不是中心对称图形,故不符合题意;
故答案为:A.
【分析】中心对称图形:把一个图形绕着某一点旋转180°后,旋转后的图形能够与原来的图形重合,据此判断即可.
2.【答案】C
【解析】【解答】解:由题意得:(n-2)×180°=3×360°,
解得:n=8;
故答案为:C.
【分析】根据多边形的内角和和外角和公式列式,求出n即可。
3.【答案】D
【解析】【解答】解: 在□ABCD中,∠A+∠B=180°,∠D=∠B,
∵∠A:∠B=1:2,
∴∠B=180°×=120°,
∴∠D=∠B=120°.
故答案为:D.
【分析】由平行四边形的性质可得∠A+∠B=180°,∠D=∠B,利用∠A:∠B=1:2求出∠B的度数即可.
4.【答案】C
【解析】【解答】∵ 只有②③两块碎玻璃的两边互相平行,且这两块有公共边
∴ 角的两边的延长线的交点就是平行四边形的顶点.
∴ 带②③两块玻璃就可以确定平行四边形的大小.
故答案为:C.
【分析】根据平行四边形的判定定理:两组对边分别平行的四边形是平行四边形.
四块玻璃中需要找到两边互相平行且可以连在一起的两块玻璃.
5.【答案】D
【解析】【解答】解:用反证法证明“四边形中至少有一个角是钝角或直角”,
可先假设四边形的四个角都是锐角.
故答案为:D.
【分析】利用反证法证明的第一步为:假设结论不成立,故只需找出至少有一个角是钝角或直角的反面即可.
6.【答案】C
【解析】【解答】∵平行四边形的对角线,交于点,已知,,
∴BO=DO=BD=5,CO=AO=AC=3,
∵的周长为15,
∴BC=15-(BO+CO)=15-(5+3)=7,
∴AD=BC=7,
故答案为:C.
【分析】先利用平行四边形的性质可得BO=DO=BD=5,CO=AO=AC=3,再利用三角形的周长公式求出BC的长,最后利用平行四边形的性质可得AD=BC.
7.【答案】A
【解析】【解答】解:依题意得:AB∥CD,AD∥BC,则四边形ABCD是平行四边形.
如图,过点A作AE⊥BC于点E,过点A作AF⊥CD于点F,
∴AE=1,AF=2,
∴BC AE=AB AF,
∴BC=2AB.
又∵AB+BC=6,
∴AB=2,BC=4
∴四边形ABCD的面积=2×2=4
故答案为:A.
【分析】本题考查了平行四边形的判定与性质.先作辅助线:过点A作AE⊥BC于点E,过点A作AF⊥CD于点F,平行四边形ABCD的面积可表示为:BC AE=AB AF,可推出:BC=2AB.进而得出AB与BC的数量关系:BC=2AB,结合AB+BC=6,可求AB和BC,即可求出平行四边形的面积.
8.【答案】C
【解析】【解答】解:延长线段BN交AC于E,
∵AN平分∠BAC,
∴∠BAN=∠EAN,
在△ABN和△AEN中
∴△ABN≌△AEN(ASA)
∴AE=AB=10,BN=EN,
而M是BC边的中点,
∴CE=2MN=2×3=6,
∴AC=AE+CE=10+6=16.
故答案为:C.
【分析】延长线段BN交AC于E,由角平分线定义可得∠BAN=∠EAN,结合已知用角边角可证△ABN≌△AEN,则AE=AB=10,BN=EN,由三角形中位线定理得CE=2MN求出CE的值,然后根据线段的构成AC=AE+CE可求解.
9.【答案】B
【解析】【解答】解:如图,连接、,
、是等腰三角形,
,,
,
,
,
,
,
,
点是的中点,点,分别是底边,的中点,
,,
,,
,
,
,
故答案为:B.
【分析】先利用等腰三角形的性质通过SAS证得,再通过三角形的内角和定理得到相等,然后利用中位线定理和外角的定义得到的和,进而求得的度数.
10.【答案】C
【解析】【解答】解:如下图所示:取AD的中点M,连接CM,AG,AC,过点A作AN⊥BC,
∵四边形ABCD是平行四边形,∠BCD=120°,AB=4,
∴∠D= 180°-∠BCD=60°,AB= CD=4,
∴AM=DM=DC=4,
∴△CDM是等边三角形,
∴∠DMC=∠MCD=60°,CM=AM,
∴∠MAC= ∠MCA=30°,
∴∠ACD =∠MCA+∠MCD= 90°,
∴,
∵∠ACN=∠DAC=30°,
∴,
∵AE = EH,GF = FH,
∴
∴EF的最大值与最小值的差为,
故答案为:C.
【分析】根据平行四边形的性质求出∠D= 180°-∠BCD=60°,AB= CD=4,再求出△CDM是等边三角形,最后利用勾股定理和直角三角形30°角的性质等计算求解即可。
11.【答案】1<x<7
【解析】【解答】解:如图,
∵四边形ABCD是平行四边形,对角线AC与BD相交于点O,且AC=6,BD=8,
∴OB=BD=4,OC=AC=3,
∴4-3<BC<4+3,
即1<BC<7,
∴ 该平行四边形的一条边x的取值范围1<x<7.
故答案为:1<x<7.
【分析】画出示意图,由平行四边形的对角线互相平分得OB=BD=4,OC=AC=3,进而根据三角形三边关系,任意两边之和大于第三边,任意两边之差小于第三边可得x的取值范围.
12.【答案】27
【解析】【解答】解:由题意得多边形边数为6+3=9,
∴ 这个多边形的对角线共有×9×(9-3)=27.
故答案为:27.
【分析】n边形从一个顶点出发可引出(n-3)条对角线,对角线的条数共有n(n-3)条,据此解答即可.
13.【答案】10
【解析】【解答】∵AC的垂直平分线交AD于点E,
∴EA=EC,
∵四边形ABCD是平行四边形,
∴CD=AB=4,AD=BC=6,
∴△CDE的周长=CD+EC+DE=CD+EA+DE=CD+AD=4+6=10.
故答案为:10.
【分析】由线段的垂直平分线的性质可得EA=EC,根据平行四边形的性质得CD=AB,AD=BC,然后根据三角形的周长等于三角形的三边之和可求解.
14.【答案】7
15.【答案】15
【解析】【解答】解:连接OE,如下图:
∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD,O为BD的中点,
∵点O、E分别是BD和BC的中点
∴OE∥CD且OE=CD=AB
∴∠EOF=∠GFO,∠OEG=∠EGF
∵FG=AB
∴OE=FG
∵∠EOF=∠GFO,OE=FG,∠OEG=∠EGF
∴△OEH≌△FGH(ASA)
∴OH=HF
∵S ABCD=BC×=AB×=60
∴S△BOE=×BE×=××BC×=×60=,
S△EOH=S△GFH=×OE×=×AB×=×60=;
∴S阴影部分=+2×=15
故答案为:15.
【分析】根据平行四边形的性质,可得AB=CD,AB∥CD;根据三角形的中点性质,可得OE∥CD且OE=CD;根据三角形全等的判定(ASA)和性质,可得OH=HF;根据平行四边形的面积公式和三角形的面积公式,即可求出阴影部分的面积.
16.【答案】
【解析】【解答】解:延长CF和AB,交于点H,如下图:
∵四边形ABCD是平行四边形
∴AB∥CD,
∴∠ACD=∠BAC=90°
∴AC=
∵AF平分∠BAC,且CF⊥AF
∴AH=AC=12,FH=FC
∵AB=5
∴BH=12-5=7
∵点E是BC的中点,FH=FC
∴EF=BH=
故答案为:.
【分析】根据平行四边形的性质,可得∠ACD=∠BAC;根据勾股定理,可得AC的长;根据等腰三角形三线合一的性质,可得AH=HC;根据三角形中线的性质,可得EF的长.
17.【答案】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∠ABC=∠CDA,
∴∠E=∠F,∠EBG=∠FDH,
∵ BE=DF ,
∴△EBG≌△FDH(ASA),
∴EG=FH.
【解析】【分析】利用性行四边形的性质可得AB∥CD,∠ABC=∠CDA,从而推出∠E=∠F,∠EBG=∠FDH,再用ASA证△EBG≌△FDH,利用全等三角形的性质即可得解.
18.【答案】证明:∵ ∠BAC=90°,AD是BC边上的中线,
∴ AD=BC,
∵ E,F分别是AB,AC的中点,
∴ EF=BC,
∴ AD=EF.
【解析】【分析】根据直角三角形的斜边中线等于斜边的一半可得AD=BC,根据三角形的中位线等于第三边的一半得EF=BC,即可求得.
19.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠GAE=∠HCF.
∵点G,H分别是AB ,CD的中点,AB= CD,∴AG=CH.∵AE=CF,
∴△AGE≌△CHF ( SAS),∴GE= HF, ∠AEG= ∠CFH,∴∠GEF =∠HFE,∴GE∥HF.又∵GE=HF,∴四边形EGFH是平行四边形.
(2)解:连结BD交AC于点O,如图.
∵四边形ABCD是平行四边形,
∴OA = OC, OB=0D. BD= 10,
∴ OB=OD=5.∵AE= CF ,OA=OC,
∴ OE=OF.∵AE+CF= EF,
∴2AE= EF=20E,∴AE=OE.又∵点G是AB的中点,∴EG是△ABO
的中位线,∴EG=OB=2.5,∴EG的长为2.5.
【解析】【分析】(1)根据平行四边形的性质可证出△AGE≌△CHF ( SAS),再根据全等三角形的性质可得出GF=HF且GF∥HF,从而证出四边形EGFH是平行四边形;
(2)根据平行四边形的性质和已知 AE+CF=EF ,可知E是OA的中点,所以EG是△ABO的中位线,根据中位线的性质可求出EG的长度.
20.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AD= BC,∠ADC+ ∠BCD =180°.∵PM∥ DC,且PM=DC,∴四边形PMCD是平行四边形,
∴PD=CM,∠PDC+∠DCM= 180°,∴∠ADP= ∠ BCM.在△ADP和△BCM中,,∴△ADP≌△BCM( SAS). .
(2)解:如图,作BH⊥AC于点H,DG⊥AC于点G,∵四边形ABCD是平行四边形,△ABC≌△CDA,∴BH= DG,
∴,即S△BCP = 2S△ABP,,即S△ADP=S△ABP.
∵△ADP≌△BCM,∴S△ADP=S△BCM,∴
【解析】【分析】(1)根据已知条件可知四边形PMCD是平行四边形,则根据平行四边形的性质可证△ADP≌△BCM;
(2)根据四边形ABCD是平行四边形,可知△ABC≌△CDA,从而得到同底边上的高BH= DG,得到S△BCP= 2S△ABP,而△ABP和△ADP是同底等高,所以面积相等,四边形BPCM的面积=△BCP的面积+△ACM的面积,而根据(1)可知△ACM的面积=△ADP的面积,从而可得出答案.
21.【答案】(1)解:PA=PE,理由如下:
连接PB,如下图:
∵四边形ABCD是平行四边形
∴AD=BC,∠ADC=180°-45°=135°
∵AD=BD
∴BD=BC
∵∠C=45°
∴三角形DBC是等腰直角三角形
∴∠BDC=45°,∠DBP=45°
∴∠PBE=∠ADC=135°
∵P是DC的中点
∴BP⊥DC,DP=BP
∴∠DPA+∠APB=∠APB+∠BPE=90°
∴∠DPA=∠BPE
∵∠DPA=∠BPE,DP=BP,∠PBE=∠ADC
∴△DPA≌△BPE(ASA)
∴PA=PE;
(2)证明:过点P作PF垂直CD交DE于点F,如下图:
∵PF⊥CD,EP⊥AP
∴∠DPE=∠APE=90°
∴∠DPA+∠APB=∠APB+∠FPE
∴∠DPA=∠FPE
∵四边形ABCD是平行四边形
∴∠C=∠DAB=45°,AB∥CD
∵AD=BD
∴∠DAB=∠DBA=45°
∴∠ADB=∠DBC=90°
∴∠PFD=45°
∴∠PFD=∠PDF
∴PD=PF
∴∠PDA=∠PFE=135°
∴△DPA≌△FPE((ASA)
∴AD=EF
∴DF=DP=DP
∵DE=DF+EF
∴DA+DP=DE;
【解析】【分析】(1)根据平行四边形的性质和等量代换原则可得BD=BC;根据等腰直角三角形的判定和性质可得∠BDC=45°,∠DBP=45°;根据三角形全等的判定(ASA)和性质可得PA=PE;
(2)根据等量代换原则可得∠DPA=∠FPE根据平行四边形的性质可得∠C=∠DAB=45°,AB∥CD;根据等腰直角三角形的性质和等量代换原则可得∠PFD=45°,∠PDA=∠PFE=135°;根据三角形全等的判定(ASA)和性质可得AD=EF;根据特殊角的三角函数的应用可得DF=DP,根据等量代换原则即可解题.
1 / 1
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
