第4章 平行四边形课时练习（含解析）

中小学教育资源及组卷应用平台
第四次 质量评估试卷
[考查范围：第4章　总分：120分]
一、选择题(每小题3分，共30分)
1．在 ABCD中，∠A∶∠B＝7∶2，则∠C等于( 　)
A．20° B．40° C．120° D．140°
2．下列平面图形中，既是中心对称图形又是轴对称图形的是(　 　)
INCLUDEPICTURE "D:\\8-35a.TIF" \* MERGEFORMATINET
第2题图 第4题
3．已知 ABCD的一边长为5，则对角线AC，BD的长可取下列数据中的(　 　)
A．2和4 B．3和4 C．4和5 D．5和6
4．如图所示，在△ABC中，D，E分别是边AC，AB的中点，连结BD.若BD平分∠ABC，则下列结论错误的是(　 　)
A．BC＝2BE B．∠A＝∠EDA C．BC＝2AD D．BD⊥AC
5．能说明命题“关于x的方程x2－4x＋m＝0一定有实数根”是假命题的反例为(　 　)
A．m＝－1 B．m＝0 C．m＝4 D．m＝5
6．已知△ABC(如图1)，按图2、图3所示的尺规作图痕迹，不需借助三角形全等，就能推出四边形ABCD是平行四边形的依据是(　 　)
A．两组对边分别平行的四边形是平行四边形 B．对角线互相平分的四边形是平行四边形
C．一组对边平行且相等的四边形是平行四边形 D．两组对边分别相等的四边形是平行四边形
第6题图 第7题图 第8题图
7．如图所示，在四边形ABCD中，AB＝CD，对角线AC，BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连结AF，CE，若DE＝BF，则下列结论：①CF＝AE；②OE＝OF；③四边形ABCD是平行四边形；④图中共有四对全等三角形．其中正确结论的个数是(　 　)
A．4个 B．3个 C．2个 D．1个
8．如图所示，已知四边形ABCD中，R，P 分别是BC，CD上的点，E，F分别是AP，RP的中点，当点P在CD上从C向D 移动而点R不动时，那么下列结论成立的是(　 　)
A．线段EF的长逐渐增大 B．线段EF的长逐渐减小
C．线段EF的长不变 D．线段EF的长与点P的位置有关
9．在平行四边形ABCD中，∠ABC的平分线BE交AD边于点E，∠DCB的平分线交AD边于点F，若AB＝7，EF＝3，则BC的长为(　 　)
A．11或17　　　　　B．11或12 C．12或17　　　　　D．11或12或17
10．已知四边形的四条边的长分别是m，n，p，q，且满足m2＋n2＋p2＋q2＝2mn＋2pq.则这个四边形是(　 　)
A．平行四边形　 B．对角线互相垂直的四边形　
C．平行四边形或对角线互相垂直的四边形　　D．对角线相等的四边形
二、填空题(每小题4分，共24分)
11．五边形的内角和是____．
12．如图，在 ABCD中，∠A＝45°，BC＝ cm，则AB与CD之间的距离为 cm.
第12题图 第13题图 第14题图 第15题图 第16题图
13．如图，在平面直角坐标系xOy中，已知点A(，0)，B(1，1).若平移点B到点D，使四边形OADB是平行四边形，则点D的坐标是 ．
14．如图，在△ABC中，D，E分别为AB，AC的中点，延长DE到点F，使EF＝DE，若AB＝10，BC＝8，则四边形BCFD的周长＝____．
15．如图，在 ABCD中，BE⊥AB交对角线AC于点E，若∠1＝20°，则∠2的度数为 °
16．如图所示，在 ABCD中，∠BCD＝30°，BC＝4，CD＝3，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连结A′C，则A′C长度的最小值是 ．
三、解答题(7个小题，共66分)
17．(6分)如图所示，在 ABCD中，AE，AF分别为BC，CD上的高，且∠EAF＝40°.求 ABCD各内角的度数．
18．(8分)用反证法证明：等腰三角形的底角必定是锐角．
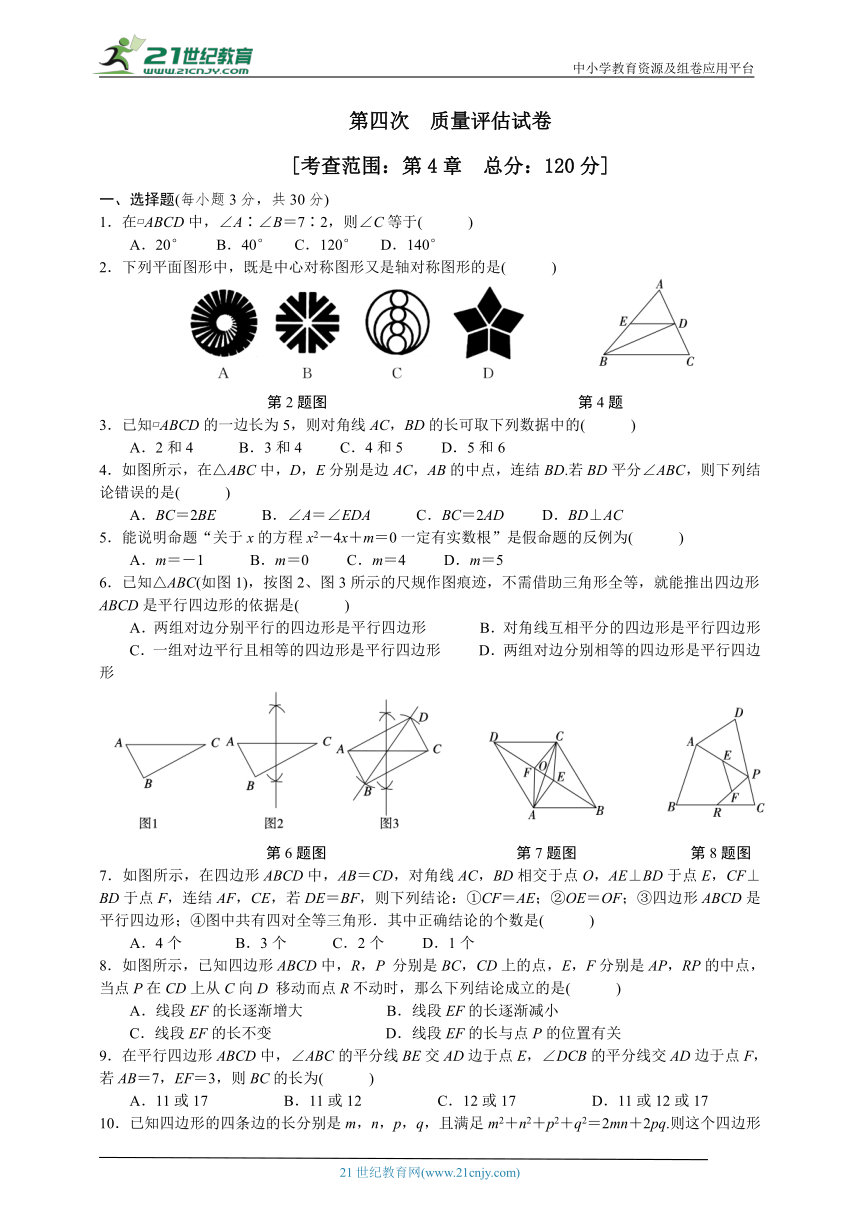
19．(10分)一天，聪聪和明明在一起下棋，这时聪聪灵机一动，象棋中也有很多数学知识，如图，我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1)，根据象棋中“马”走“日”的规定，若“马”的位置在图中的点P.
(1)写出下一步“马”可能到达的点的坐标；
(2)明明想了想，他还有两个问题：
①如果顺次连结(1)中的所有点，得到的图形是_ _图形(选填“中心对称”或“轴对称”)；
②指出(1)中关于点P成中心对称的点．
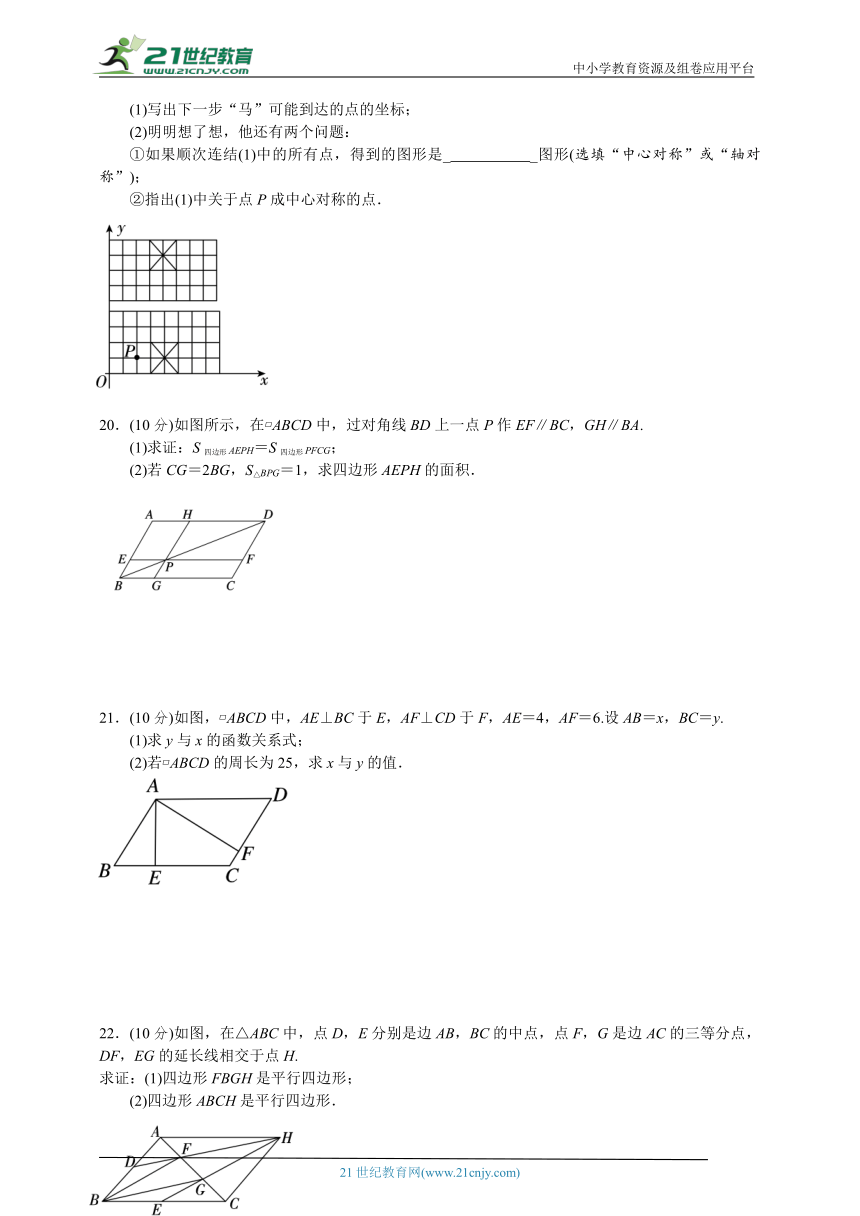
20．(10分)如图所示，在 ABCD中，过对角线BD上一点P作EF∥BC，GH∥BA.
(1)求证：S四边形AEPH＝S四边形PFCG；
(2)若CG＝2BG，S△BPG＝1，求四边形AEPH的面积．
21．(10分)如图， ABCD中，AE⊥BC于E，AF⊥CD于F，AE＝4，AF＝6.设AB＝x，BC＝y.
(1)求y与x的函数关系式；
(2)若 ABCD的周长为25，求x与y的值．
22．(10分)如图，在△ABC中，点D，E分别是边AB，BC的中点，点F，G是边AC的三等分点，DF，EG的延长线相交于点H.
求证：(1)四边形FBGH是平行四边形；
(2)四边形ABCH是平行四边形．
23．(12分)如图，△ABC是等边三角形，D是边BC上的一点，以AD为边作等边△ADE，过点C作CF∥DE交AB于点F.
(1)若点D是BC边的中点，如图1，求证：EF＝CD；
(2)在(1)的条件下直接写出△AEF和△ABC的面积比；
(3)若D是BC边上的任意一点(除B，C外)，如图2，那么(1)中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．
第四次 质量评估试卷答案
D 2．B 3．D　4．C 5．D 6．B 7．B 8．C 9．A
10.【解析】 m2＋n2＋p2＋q2＝2mn＋2pq可化简为
(m－n)2＋(p－q)2＝0，
∴m＝n，p＝q.
∵m，n，p，q分别为四边形的四边长，
∴当m，n为对边，p，q为对边时，可确定其为平行四边形；
当m，n为邻边时，可以证明有两个顶点在一条对角线的垂直平分线上，
∴四边形是对角线互相垂直的四边形．
11.540° 12.1 13.(＋1，1)_ 14.26 15.110 16.5
17.解：∵AE，AF分别为BC，CD上的高，
∴∠AEC＝∠AFC＝90°.
∵∠EAF＝40°，
∴∠C＝360°－∠EAF－∠AEC－∠AFC＝140°.
∵四边形ABCD是平行四边形，
∴∠BAD＝∠C＝140°，∠B＝∠D＝180°－∠C＝40°，
∴ ABCD各内角的度数分别为：140°，40°，140°，40°.
18.证明：①设等腰三角形底角∠B，∠C都是直角，则∠B＋∠C＝180°，所以∠A＋∠B＋∠C＝180°＋∠A＞180°，这与三角形内角和等于180°矛盾；
INCLUDEPICTURE "D:\\+17.EPS" \* MERGEFORMATINET INCLUDEPICTURE "D:\\+17.EPS" \* MERGEFORMATINET INCLUDEPICTURE "D:\\+17.EPS" \* MERGEFORMATINET
②设等腰三角形的底角∠B，∠C都是钝角，则∠B＋∠C＞180°，所以∠A＋∠B＋∠C＞180°，这与三角形内角和等于180°矛盾．
综上所述，①，②的假设错误，所以∠B，∠C只能为锐角，
故等腰三角形的底角必为锐角．
19.解：(1)根据分析可得，下一步“马”可能到达的点的坐标为：
(0，0)，(0，2)，(1，3)，(3，3)，(4，2)，(4，0).
(2)①__轴对称__ ②根据中心对称的定义可得，(1)中关于点P成中心对称的点为：点(0，0)和点(4，2)；点(0，2)和点(4，0).
20.解：(1)证明：∵EF∥BC，GH∥BA，
∴四边形HPFD，BEPG，AEPH，CFPG为平行四边形，
∴S△PEB＝S△BGP，S△PHD＝S△DFP，S△ABD＝S△CDB.
∴S△ABD－S△PEB－S△PHD＝S△CDB－S△BGP－S△DFP，即S四边形AEPH＝S四边形PFCG.
(2)∵CG＝2BG，S△BPG＝1，
∴S四边形AEPH＝S四边形PFCG＝4×1＝4.
21.解：(1)根据平行四边形的面积公式得，S平行四边形ABCD＝AB·AF＝BC·AE，
∴6x＝4y，∴y＝x.
(2)∵ ABCD的周长为25，
∴2(x＋y)＝25，∴y＝，
把y＝x代入y＝中，得x＝，
解得x＝5，∴y＝.
22.证明：(1)∵点F，G是边AC的三等分点，
∴F，G分别是AG，CF的中点．
∵点D是AB的中点，
∴DF∥BG，即FH∥BG.
同理，GH∥BF，
∴四边形FBGH是平行四边形．
(2)如图，连结BH，交FG于点O.
∵四边形FBGH是平行四边形，
∴OB＝OH，OF＝OG.
∵AF＝CG，∴OA＝OC，
∴四边形ABCH是平行四边形．
23.解：(1)证明：∵△ABC是等边三角形，D是BC的中点，
∴AD⊥BC，且∠BAD＝∠BAC＝30°.
∵△AED是等边三角形，∴AD＝AE，∠ADE＝60°，
∴∠EDB＝90°－∠ADE＝90°－60°＝30°.
∵ED∥CF，∴∠FCB＝∠EDB＝30°.
∵∠ACB＝60°，∴∠ACF＝∠ACB－∠FCB＝30°，
∴∠ACF＝∠BAD＝30°.
在△ABD和△CAF中，
∵
∴△ABD≌△CAF(ASA)，∴AD＝CF.
∵AD＝ED，∴ED＝CF.
又∵ED∥CF，
∴四边形EDCF是平行四边形，∴EF＝CD.
(2)△AEF和△ABC的面积比为1∶4.
(3)成立．证明如下：
∵ED∥FC，∴∠EDB＝∠FCB.
∵∠AFC＝∠B＋∠BCF＝60°＋∠BCF，
∠BDA＝∠ADE＋∠EDB＝60°＋∠EDB，
∴∠AFC＝∠BDA.
在△ABD和△CAF中，
∵
∴△ABD≌△CAF(AAS)，∴AD＝CF.
∵AD＝ED，∴ED＝CF.又∵ED∥CF，
∴四边形EDCF是平行四边形，∴EF＝CD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)