第4章 平行四边形阶段性测试(七)课时练习(含解析)
文档属性
| 名称 | 第4章 平行四边形阶段性测试(七)课时练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 21:13:15 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
阶 段 性 测 试(七)
[考查范围:第4章 4.4~4.6 总分:100分]
一、选择题(每小题5分,共40分)
1.用反证法证明“x>1”时应假设( )
A.x>-1 B.x<1 C.x=1 D.x≤1
2.在四边形ABCD中,对角线AC,BD相交于点O,∠ADB=∠CBD,添加下列一个条件后,仍不能判定四边形ABCD是平行四边形的是( D )
A.∠ABD=∠CDB B.∠DAB=∠BCD C.∠ABC=∠CDA D.∠DAC=∠BCA
3.根据图中所给边长的长度及角度,判断下列选项中的四边形是平行四边形的是( )
4. 如图,点D、E分别是△ABC边BA、BC的中点,AC=3,则DE的长为( )
A.2 B. C.3 D.
5.如图,平行四边形ABCD中,E,F分别为边AB,DC的中点,则图中平行四边形的个数是( )
A.3 B.4 C.5 D.6
第5题图 第6题图 第7题图
6.如图,在 ABCD中,E,F是对角线AC上的两点,且AE=CF,有下列结论:①BE=DF;②BE∥DF;③AB=DE;④四边形EBFD为平行四边形;⑤AF=CE;⑥S△ADE=S△ABE.其中正确结论的个数是( )
A.3 B.4 C.5 D.6
7.如图,将△ABC绕边AC的中点O顺时针旋转180°.嘉淇发现,旋转后的△CDA与△ABC构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵CB=AD,”和“∴四边形…”之间作补充,下列正确的是( )
A.嘉淇推理严谨,不必补充 B.应补充:且AB=CD
C.应补充:且AB∥CD D.应补充:且OA=OC
8.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为 N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )
A. B.2 C. D.3
二、填空题(每小题5分,共25分)
9.如图所示,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连结AB,AD,CD,得 ABCD,判定的依据是 .
10.用反证法证明“三角形三个内角中最多有一个直角”的第一步应假设:
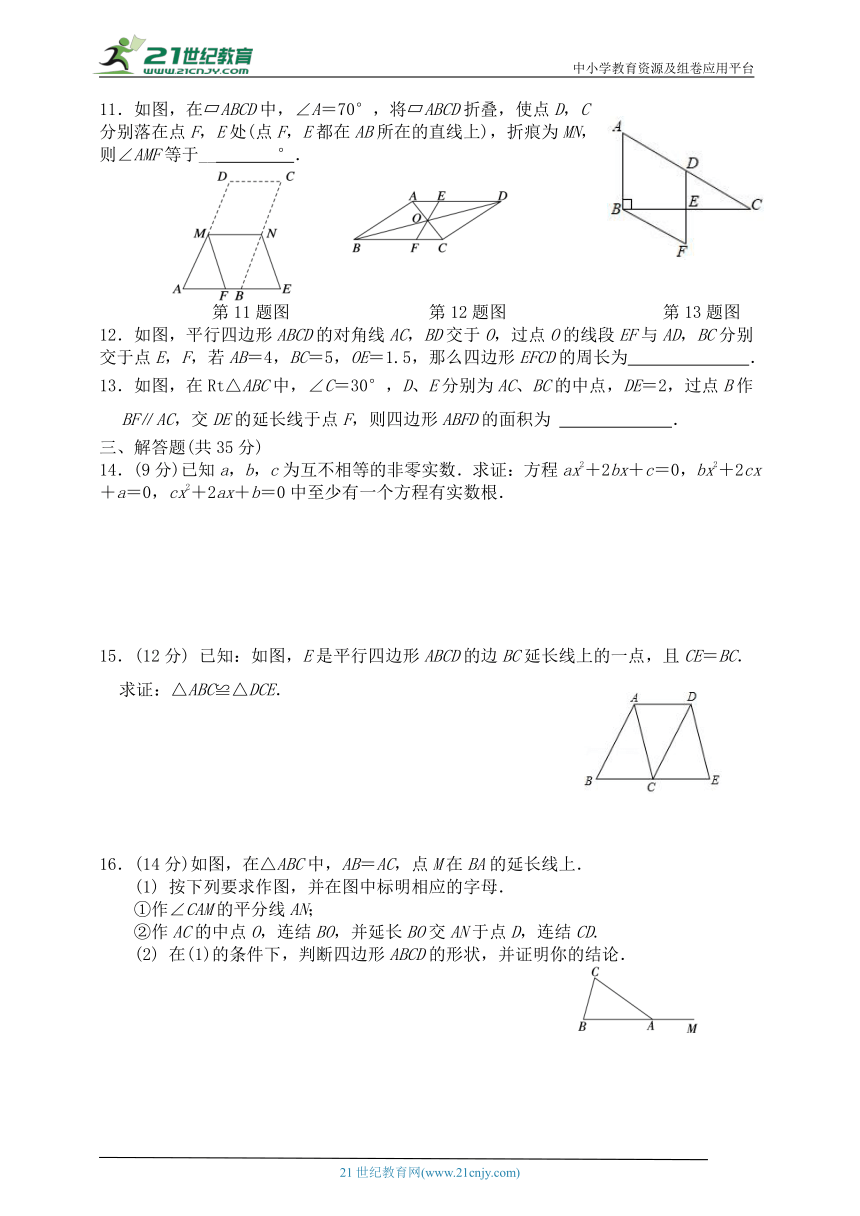
11.如图,在 ABCD中,∠A=70°,将 ABCD折叠,使点D,C分别落在点F,E处(点F,E都在AB所在的直线上),折痕为MN,则∠AMF等于__ °.
第11题图 第12题图 第13题图
12.如图,平行四边形ABCD的对角线AC,BD交于O,过点O的线段EF与AD,BC分别交于点E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为 .
13.如图,在Rt△ABC中,∠C=30°,D、E分别为AC、BC的中点,DE=2,过点B作BF∥AC,交DE的延长线于点F,则四边形ABFD的面积为 .
三、解答题(共35分)
14.(9分)已知a,b,c为互不相等的非零实数.求证:方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0中至少有一个方程有实数根.
15.(12分) 已知:如图,E是平行四边形ABCD的边BC延长线上的一点,且CE=BC.
求证:△ABC≌△DCE.
16.(14分)如图,在△ABC中,AB=AC,点M在BA的延长线上.
(1) 按下列要求作图,并在图中标明相应的字母.
①作∠CAM的平分线AN;
②作AC的中点O,连结BO,并延长BO交AN于点D,连结CD.
(2) 在(1)的条件下,判断四边形ABCD的形状,并证明你的结论.
阶 段 性 测 试(七)答案
D 2.D 3.B 4.D 5.D 6.C 7.B 8.C 9.__两组对边分别相等的四边形是平行四边形__
10._三角形三个内角中最少有两个直角__11._40° 12.12 13.8
14.证明:假设题中的三个方程都没有实数根,不妨设这三个方程的根的判别式为Δ1,Δ2,Δ3,则有
Δ1=4b2-4ac<0①,Δ2=4c2-4ab<0②,Δ3=4a2-4bc<0③.
由①+②+③,得Δ1+Δ2+Δ3<0.
即4a2+4b2+4c2-4ab-4ac-4bc
=2(2a2+2b2+2c2-2ab-2bc-2ca)
=2[(a2-2ab+b2)+(b2-2bc+c2)+(c2-2ca+a2)]
=2[(a-b)2+(b-c)2+(c-a)2]<0.④
由题意知a,b,c互不相等,所以④式不成立.
故三个方程中至少有一个方程有实数根.
15.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠B=∠DCE,
在△ABC和△DCE中,
∴△ABC≌△DCE(SAS).
16.解:(1)作∠MAC的角
INCLUDEPICTURE "D:\\+11.EPS" \* MERGEFORMATINET INCLUDEPICTURE "D:\\+11.EPS" \* MERGEFORMATINET INCLUDEPICTURE "D:\\+11.EPS" \* MERGEFORMATINET INCLUDEPICTURE "../+11.EPS" \* MERGEFORMAT
平分线AN,作AC的中垂线得到AC的中点O,连结BO,并延长BO交AN于点D,连结CD,如图.
(2)四边形ABCD是平行四边形.
理由如下:
∵AB=AC,∴∠ACB=∠ABC.
∵AN平分∠MAC,∴∠MAN=∠CAN.
∵∠MAC=∠ABC+∠ACB,
∴∠ACB=∠CAD.
∴BC∥AD.
∵AC的中点是O,∴AO=CO.
在△BOC和△DOA中,
∴△BOC≌△DOA,
∴BC=DA.又∵BC∥DA,
∴四边形ABCD是平行四边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
阶 段 性 测 试(七)
[考查范围:第4章 4.4~4.6 总分:100分]
一、选择题(每小题5分,共40分)
1.用反证法证明“x>1”时应假设( )
A.x>-1 B.x<1 C.x=1 D.x≤1
2.在四边形ABCD中,对角线AC,BD相交于点O,∠ADB=∠CBD,添加下列一个条件后,仍不能判定四边形ABCD是平行四边形的是( D )
A.∠ABD=∠CDB B.∠DAB=∠BCD C.∠ABC=∠CDA D.∠DAC=∠BCA
3.根据图中所给边长的长度及角度,判断下列选项中的四边形是平行四边形的是( )
4. 如图,点D、E分别是△ABC边BA、BC的中点,AC=3,则DE的长为( )
A.2 B. C.3 D.
5.如图,平行四边形ABCD中,E,F分别为边AB,DC的中点,则图中平行四边形的个数是( )
A.3 B.4 C.5 D.6
第5题图 第6题图 第7题图
6.如图,在 ABCD中,E,F是对角线AC上的两点,且AE=CF,有下列结论:①BE=DF;②BE∥DF;③AB=DE;④四边形EBFD为平行四边形;⑤AF=CE;⑥S△ADE=S△ABE.其中正确结论的个数是( )
A.3 B.4 C.5 D.6
7.如图,将△ABC绕边AC的中点O顺时针旋转180°.嘉淇发现,旋转后的△CDA与△ABC构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵CB=AD,”和“∴四边形…”之间作补充,下列正确的是( )
A.嘉淇推理严谨,不必补充 B.应补充:且AB=CD
C.应补充:且AB∥CD D.应补充:且OA=OC
8.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为 N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )
A. B.2 C. D.3
二、填空题(每小题5分,共25分)
9.如图所示,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连结AB,AD,CD,得 ABCD,判定的依据是 .
10.用反证法证明“三角形三个内角中最多有一个直角”的第一步应假设:
11.如图,在 ABCD中,∠A=70°,将 ABCD折叠,使点D,C分别落在点F,E处(点F,E都在AB所在的直线上),折痕为MN,则∠AMF等于__ °.
第11题图 第12题图 第13题图
12.如图,平行四边形ABCD的对角线AC,BD交于O,过点O的线段EF与AD,BC分别交于点E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为 .
13.如图,在Rt△ABC中,∠C=30°,D、E分别为AC、BC的中点,DE=2,过点B作BF∥AC,交DE的延长线于点F,则四边形ABFD的面积为 .
三、解答题(共35分)
14.(9分)已知a,b,c为互不相等的非零实数.求证:方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0中至少有一个方程有实数根.
15.(12分) 已知:如图,E是平行四边形ABCD的边BC延长线上的一点,且CE=BC.
求证:△ABC≌△DCE.
16.(14分)如图,在△ABC中,AB=AC,点M在BA的延长线上.
(1) 按下列要求作图,并在图中标明相应的字母.
①作∠CAM的平分线AN;
②作AC的中点O,连结BO,并延长BO交AN于点D,连结CD.
(2) 在(1)的条件下,判断四边形ABCD的形状,并证明你的结论.
阶 段 性 测 试(七)答案
D 2.D 3.B 4.D 5.D 6.C 7.B 8.C 9.__两组对边分别相等的四边形是平行四边形__
10._三角形三个内角中最少有两个直角__11._40° 12.12 13.8
14.证明:假设题中的三个方程都没有实数根,不妨设这三个方程的根的判别式为Δ1,Δ2,Δ3,则有
Δ1=4b2-4ac<0①,Δ2=4c2-4ab<0②,Δ3=4a2-4bc<0③.
由①+②+③,得Δ1+Δ2+Δ3<0.
即4a2+4b2+4c2-4ab-4ac-4bc
=2(2a2+2b2+2c2-2ab-2bc-2ca)
=2[(a2-2ab+b2)+(b2-2bc+c2)+(c2-2ca+a2)]
=2[(a-b)2+(b-c)2+(c-a)2]<0.④
由题意知a,b,c互不相等,所以④式不成立.
故三个方程中至少有一个方程有实数根.
15.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠B=∠DCE,
在△ABC和△DCE中,
∴△ABC≌△DCE(SAS).
16.解:(1)作∠MAC的角
INCLUDEPICTURE "D:\\+11.EPS" \* MERGEFORMATINET INCLUDEPICTURE "D:\\+11.EPS" \* MERGEFORMATINET INCLUDEPICTURE "D:\\+11.EPS" \* MERGEFORMATINET INCLUDEPICTURE "../+11.EPS" \* MERGEFORMAT
平分线AN,作AC的中垂线得到AC的中点O,连结BO,并延长BO交AN于点D,连结CD,如图.
(2)四边形ABCD是平行四边形.
理由如下:
∵AB=AC,∴∠ACB=∠ABC.
∵AN平分∠MAC,∴∠MAN=∠CAN.
∵∠MAC=∠ABC+∠ACB,
∴∠ACB=∠CAD.
∴BC∥AD.
∵AC的中点是O,∴AO=CO.
在△BOC和△DOA中,
∴△BOC≌△DOA,
∴BC=DA.又∵BC∥DA,
∴四边形ABCD是平行四边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
