九年级数学上册试题 3.8 弧长及扇形的面积同步测试-浙教版(含解析)
文档属性
| 名称 | 九年级数学上册试题 3.8 弧长及扇形的面积同步测试-浙教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 07:22:40 | ||
图片预览


文档简介
3.8 弧长及扇形的面积
一、单选题
1.如图,的半径为3,是的弦,直径,,则的长为( )
A. B. C. D.
2.如图,在中,,将绕点按逆时针方向旋转后得到,则阴影部分面积为( )
A.8 B.9 C.16 D.18
3.如图,∠MON=40°,以O为圆心,4为半径作弧交OM于点A,交ON于点B,分别以点A,B为圆心,大于的长为半径画弧,两弧在∠MON的内部相交于点C,画射线OC交于点D,E为OA上一动点,连接BE,DE,则阴影部分周长的最小值为( )
A. B. C. D.
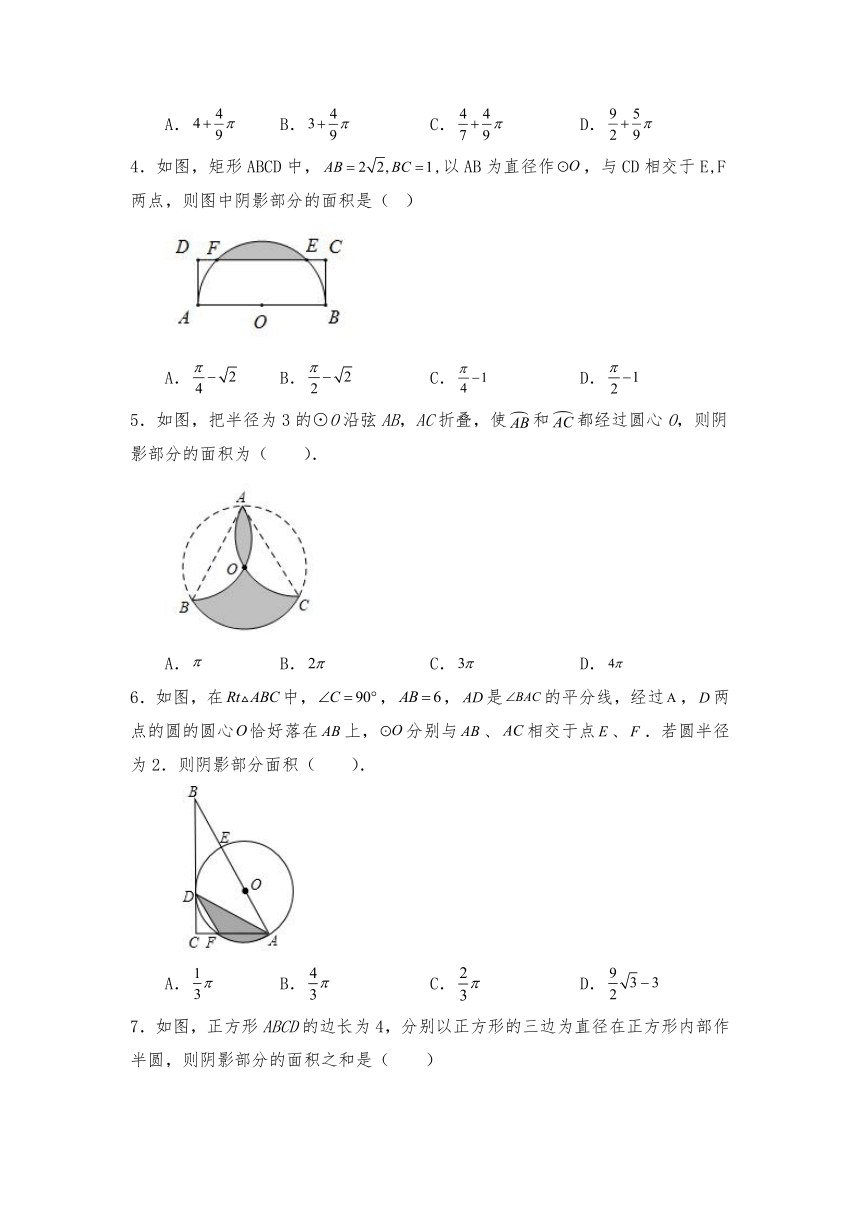
4.如图,矩形ABCD中,,以AB为直径作,与CD相交于E,F两点,则图中阴影部分的面积是( )
A. B. C. D.
5.如图,把半径为3的⊙O沿弦AB,AC折叠,使和都经过圆心O,则阴影部分的面积为( ).
A. B. C. D.
6.如图,在中,,,是的平分线,经过,两点的圆的圆心恰好落在上,分别与、相交于点、.若圆半径为2.则阴影部分面积( ).
A. B. C. D.
7.如图,正方形ABCD的边长为4,分别以正方形的三边为直径在正方形内部作半圆,则阴影部分的面积之和是( )
A.8 B.4 C.16π D.4π
8.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A. B. C. D.
9.如图,矩形A′B′C′D′是由矩形ABCD绕C点顺时针旋转而得,且点A、C、D′在同一条直线上,在Rt△ABC中,若AB=2,AD=2,则对角线AC旋转所扫过的扇形面积为( )
A. B. C. D.
10.如图,在矩形中,为对角线,,,以为圆心,长为半径画弧,交于点,交于点,则阴影部分的面积为( )
A. B. C. D.
二、填空题
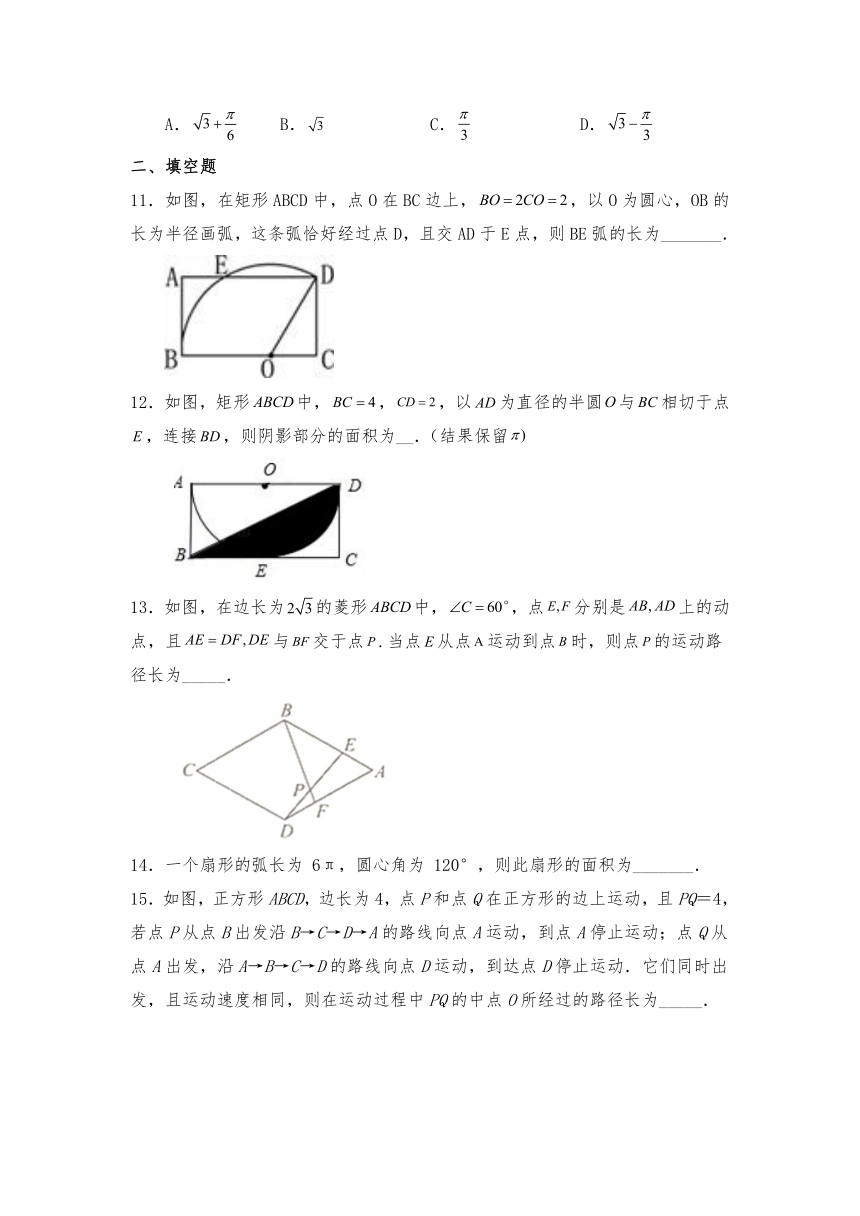
11.如图,在矩形ABCD中,点O在BC边上,,以O为圆心,OB的长为半径画弧,这条弧恰好经过点D,且交AD于E点,则BE弧的长为_______.
12.如图,矩形中,,,以为直径的半圆与相切于点,连接,则阴影部分的面积为__.(结果保留
13.如图,在边长为的菱形中,,点分别是上的动点,且与交于点.当点从点运动到点时,则点的运动路径长为_____.
14.一个扇形的弧长为 6π,圆心角为 120°,则此扇形的面积为_______.
15.如图,正方形ABCD,边长为4,点P和点Q在正方形的边上运动,且PQ=4,若点P从点B出发沿B→C→D→A的路线向点A运动,到点A停止运动;点Q从点A出发,沿A→B→C→D的路线向点D运动,到达点D停止运动.它们同时出发,且运动速度相同,则在运动过程中PQ的中点O所经过的路径长为_____.
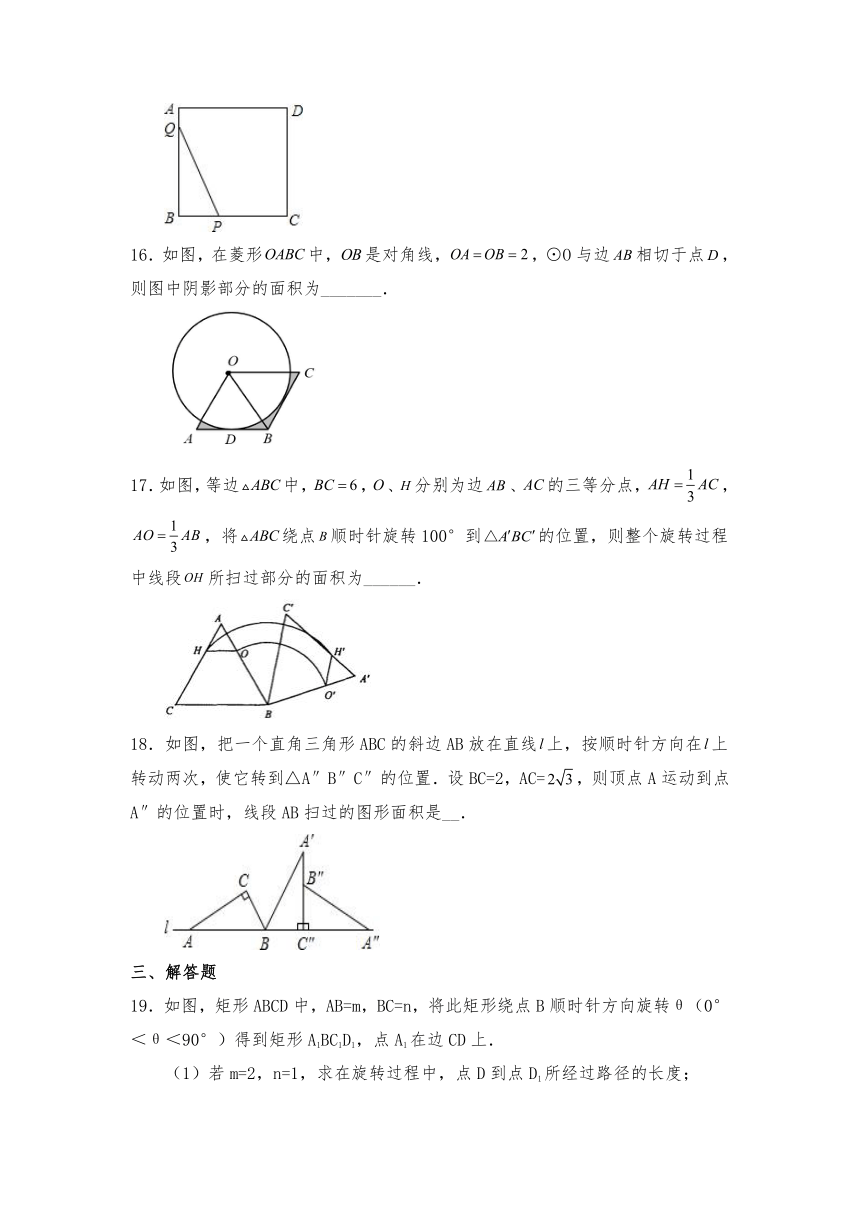
16.如图,在菱形中,是对角线,,⊙O与边相切于点,则图中阴影部分的面积为_______.
17.如图,等边中,,、分别为边、的三等分点,,,将绕点顺时针旋转100°到的位置,则整个旋转过程中线段所扫过部分的面积为______.
18.如图,把一个直角三角形ABC的斜边AB放在直线上,按顺时针方向在上转动两次,使它转到△A″B″C″的位置.设BC=2,AC=,则顶点A运动到点A″的位置时,线段AB扫过的图形面积是__.
三、解答题
19.如图,矩形ABCD中,AB=m,BC=n,将此矩形绕点B顺时针方向旋转θ(0°<θ<90°)得到矩形A1BC1D1,点A1在边CD上.
(1)若m=2,n=1,求在旋转过程中,点D到点D1所经过路径的长度;
(2)将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2,点D2在BC的延长线上,设边A2B与CD交于点E,若=﹣1,求的值.
20.在扇形中,半径,点P在OA上,连结PB,将沿PB折叠得到.
(1)如图1,若,且与所在的圆相切于点B.
①求的度数.
②求AP的长.
(2)如图2,与相交于点D,若点D为的中点,且,求的长.
21.如图,的直径为,弦为的平分线交于点.
(1)求的长;
(2)试探究之间的等量关系,并证明你的结论;
(3)连接为半圆上任意一点,过点作于点,设的内心为,当点在半圆上从点运动到点时,求内心所经过的路径长
22.如图,正方形ABCD的边长为4cm,点E、F分别从点D和点C出发,沿着射线DA、射线CD运动,且DE=CF,直线AF、直线BE交于H点.
(1)当点E从点D向点A运动的过程中:
①求证:AF⊥BE;
②在图中画出点H运动路径并求出点H运动的路径长;
(2)在整个运动过程中:
①线段DH长度的最小值为______.
②线段DH长度的最大值为_________ .
23.如图,在半径为2的⊙O中,点Q为优弧MN的中点,圆心角∠MON=60°,在弧QN上有一动点P,且点P到弦MN所在直线的距离为x.
(1) 求弦MN的长;
(2) 试求阴影部分面积y与x的函数关系式,并写出自变量x的取值范围;
(3) 试分析比较,阴影部分面积y与的大小关系.
24.已知:如图,BC为⊙O的弦,点A为⊙O上一个动点,△OBC的周长为16.过C作CD∥AB交⊙O于D,BD与AC相交于点P,过点P作PQ∥AB交于Q,设∠A的度数为α.
(1)如图1,求∠COB的度数(用含α的式子表示);
(2)如图2,若∠ABC=90°时,AB=8,求阴影部分面积(用含α的式子表示);
(3)如图1,当PQ=2,求的值.
答案
一、单选题
1.C
【分析】连接OC,利用垂径定理以及圆心角与圆周角的关系求出;再利用弧长公式即可求出的长.
解:连接OC
(同弧所对的圆心角是圆周角的2倍)
∵直径
∴=(垂径定理)
∴
故选C
2.C
【分析】旋转后△ABC≌△A1BC1,则阴影部分面积=S△ABA1+S△A1BC1-S△ABC.
解:∵在△ABC中,AB=6,旋转后△ABC≌△A1BC1,
∴A1B=AB=6,
∴△A1BA是等腰三角形,∠A1BA=30°,
∴S△ABA1==9,
∵阴影部分面积=S△ABA1+S△A1BC1-S△ABC,
∴阴影部分面积=9.
3.A
【分析】利用作图可知OA=OB=OD=4,∠BOD=∠DOA=20°,即可求出的长度,作D点关于OM的对称点F,连接EF、OF、BF,根据∠FOA=∠DOA=20°,OF=OD=OB,ED=EF,得到∠BOF=60°,得到△OBF是等边三角形,则有BE+DE=BE+EF的最小值为BF=4(B、E、F三点在同一直线上),则问题得解.
解:作D点关于OM的对称点F,连接EF、OF、BF,如图所示:
根据题条件可知,∠BOD=∠DOA=20°,
∴,
∵D、F关于OM对称,
∴∠FOA=∠DOA=20°,OF=OD=OB,ED=EF,
∴∠BOF=60°,
∴△OBF是等边三角形,BF=OB=4,
∵DE=EF,
∴BE+DE=BE+EF,
∵的长度为定值,
∴要想求阴影部分的周长最小即求BE+DE的最小值,
又∵BE+DE=BE+EF,
∴要求BE+EF的最小值,
由图可知当B、E、F三点在同一直线上时,BE+EF=BF,此时有最小值,
∵△OBF是等边三角形,BF=OB=4,
∴BE+EF=BF=4此时最小,
∴阴影部分的周长最小值为:,
故选:A.
4.D
【分析】连接OF、OE,过点O作OH⊥CD于点H,利用勾股定理求出FH=1,得到∠FOH=45°,根据等腰三角形的三线合一的性质得到EF=2FH=2,∠EOF=90°,再利用扇形EOF的面积减去△EOF的面积即可得到答案.
解:如图,连接OF、OE,过点O作OH⊥CD于点H,
∵OF=AB=,OH=BC=1,∠OHF=90°,
∴,
∴FH=OH,
∴∠FOH=45°,
∵OF=OE,
∴EF=2FH=2,∠EOF=90°,
∴阴影部分的面积是.
故选:D
5.C
【分析】阴影部分面积是不规则图形,因此首先连接OA,OB,OC,将不规则图形转化为规则图形求面积.求扇形面积需知道圆心角的度数,因此作圆心O关于弦AB,AC的对称点,即可得到OE=OA,即可得到∠AOC=∠AOB=∠BOC=120°,从而求出扇形BOC的面积即阴影部分面积.
解:如图,连接OA,OB,OC,并做O点关于AC的对称点D点,连接OD,叫AC于点E.
∵OA=OB=OC,
∴,
∴,
∵O点、D点关于AC的对称,
∴OE=DE=1,
∴OE=OA=OC,
∴∠OCE=∠OAE =30°
∴∠AOC=120°
同理可得∠AOB=120°,
∴∠BOC=120°,
∴,
故选C.
6.C
【分析】连接OD,OF.首先证明OD∥AC,推出S阴=S扇形OFA,再证明△AOF是等边三角形即可解决问题.
解:连接OD,OF.
∵AD是∠BAC的平分线,
∴∠DAB=∠DAC,
∵OD=OA,
∴∠ODA=∠OAD,
∴∠ODA=∠DAC,
∴OD∥AC,
∴∠ODB=∠C=90°,
∴S△AFD=S△OFA,
∴S阴=S扇形OFA,
∵OD=OA=2,AB=6,
∴OB=4,
∴OB=2OD,
∴∠B=30°,
∴∠A=60°,
∵OF=OA,
∴△AOF是等边三角形,
∴∠AOF=60°,
∴S阴=S扇形OFA=.
故选:C.
7.A
【分析】先判断出两半圆交点为正方形的中心,连接OA,OD,则可得出所产生的四个小弓形的面积相等,先得出2个小弓形的面积,即可求阴影部分面积.
解:由题意,易知两半圆的交点即为正方形的中心,设此点为O,连接AO,DO,
则图中的四个小弓形的面积相等,
∵两个小弓形面积=S半圆AOD-S△AOD=S半圆AOD-S正方形ABCD,
又正方形ABCD的边长为4,得各半圆的半径为2,
∴两个小弓形面积=×π×22﹣×4×4=2π﹣4,
∴S阴影=2×S半圆﹣4个小弓形面积=π 22﹣2(2π﹣4)=8,
故选:A.
8.B
解:分析:连接AC,AG,由OG垂直于AB,利用垂径定理得到O为AB的中点,由G的坐标确定出OG的长,在直角三角形AOG中,由AG与OG的长,利用勾股定理求出AO的长,进而确定出AB的长,由CG+GO求出OC的长,在直角三角形AOC中,利用勾股定理求出AC的长,由CF垂直于AE,得到三角形ACF始终为直角三角形,点F的运动轨迹为以AC为直径的半径,如图中红线所示,当E位于点B时,CO⊥AE,此时F与O重合;当E位于D时,CA⊥AE,此时F与A重合,可得出当点E从点B出发顺时针运动到点D时,点F所经过的路径长,在直角三角形ACO中,利用锐角三角函数定义求出∠ACO的度数,进而确定出所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出的长.
解:连接AC,AG,
∵GO⊥AB,
∴O为AB的中点,即AO=BO=AB,
∵G(0,1),即OG=1,
∴在Rt△AOG中,根据勾股定理得:AO=,
∴AB=2AO=2,
又CO=CG+GO=2+1=3,
∴在Rt△AOC中,根据勾股定理得:AC=,
∵CF⊥AE,
∴△ACF始终是直角三角形,点F的运动轨迹为以AC为直径的半圆,
当E位于点B时,CO⊥AE,此时F与O重合;当E位于D时,CA⊥AE,此时F与A重合,
∴当点E从点B出发顺时针运动到点D时,点F所经过的路径长,
在Rt△ACO中,tan∠ACO=,
∴∠ACO=30°,
∴度数为60°,
∵直径AC=2,
∴的长为,
则当点E从点B出发顺时针运动到点D时,点F所经过的路径长.
故选B.
9.A
解:根据题意得:∠ACB=30°,则∠A′CB′=30°,则∠ACA′=90°+30°=120°,根 据勾股定理可得AC=4,则S=.
10.D
【分析】如图,连接,过作于点,此时根据直角三角形的性质求得,,再根据等边三角形判定得出为等边三角形,进而将问题转化到新的三角形之中,利用勾股定理求得,最终求阴影部分的面积转化为求解即可.
解:如下图,连接,过作于点,
在矩形中,
∵,, ,
∴,,
又∵,,
∴为等边三角形,
∴,,
∴,
故选:D.
二、填空题
11.
分析:连接OE,根据矩形的性质,得到∠C=90°,进而得到∠ODC=90°,然后得出等边三角形EOD,可求∠BOE=60°,再根据弧长公式求解即可.
解:连接OE
∵矩形ABCD中,BO=2CO=2
∴DO=2CO=2
∴∠ODC=30°
∴∠EDO=∠DOC=60°
∵OE=OD
∴∠EOD=60°
∴∠BOE=60°
∴BE弧的长为.
故答案为.
12.π.
【分析】如图所示,连接OE交BD于点F,利用切线的性质得OD=2,OE⊥BC,易得四边形OECD为正方形,再证△EFB≌△OFD,即可将阴影部分面积转化为扇形OED的面积,最后利用扇形面积公式求解即可得出答案.
解:如图所示,连接OE交BD于点F,
∵以AD为直径的半圆O与BC相切于点E,
∴OD=2,OE⊥BC,
∴OE=OD=2,
在矩形中,
∵
∴四边形OECD为正方形,
∴CE=OD=2,
∴BE=BC-CE=2,
∴BE=DO,
∵AD//BC,
∴
∴△EFB≌△OFD,
∴阴影部分的面积= .
故答案为π.
13.
【分析】根据题意证得,推出∠BPE =60,∠BPD =120,得到C、B、P、D四点共圆,知点的运动路径长为的长,利用弧长公式即可求解.
解:连接BD,
∵菱形中,,
∴∠C=∠A=60,AB=BC=CD=AD,
∴△ABD和△CBD都为等边三角形,
∴BD=AD,∠BDF=∠DAE=60,
∵DF=AE,
∴,
∴∠DBF=∠ADE,
∵∠BPE=∠BDP+∠DBF =∠BDP+∠ADE=∠BDF =60,
∴∠BPD=180-∠BPE=120,
∵∠C=60,
∴∠C+∠BPD =180,
∴C、B、P、D四点共圆,即⊙O是的外接圆,
∴当点从点运动到点时,则点的运动路径长为的长,
∴∠BOD =2∠BCD =120,
作OG⊥BD于G,
根据垂径定理得:BG=GD=BD=,∠BOG =∠BOD =60,
∵,即,
∴,
从而点的路径长为.
14.27π
【分析】先根据弧长公式求出扇形的半径,再根据扇形的面积公式求解即可.
解:设扇形的半径为r,则
解得:
∴扇形的面积
故答案为:.
15.
解:画出点O运动的轨迹,如图虚线部分,
则点P从B到A的运动过程中,PQ的中点O所经过的路线长等于3π,
故答案为:3π.
16.
【分析】连接OD,先求出等边三角形OAB的面积,再求出扇形的面积,即可求出阴影部分的面积.
解:如图,连接OD,
∵AB是切线,则OD⊥AB,
在菱形中,
∴,
∴△AOB是等边三角形,
∴∠AOB=∠A=60°,
∴OD=,
∴,
∴扇形的面积为:,
∴阴影部分的面积为:;
故答案为:.
17.
【分析】连接BH、,过点H作HMBC于点M,根据等边三角形的性质和已知条件可求得AH=AO=2,HC=OB=4,在Rt△HCM中,求得CM=2,HM=2,在Rt△HBM中,求得,由旋转可得△HOB≌△,,即可得线段所扫过部分的面积为,由此即可求解.
解:连接BH、,过点H作HMBC于点M,
∵为等边三角形,,
∴,∠C=60°,
∵,,
∴AH=AO=2,
∴HC=OB=4,
在Rt△HCM中,∠C=60°,HC=4,
∴CM=2,HM=2,
∵BC=6,
∴BM=4,
在Rt△HBM中,BM=4,HM=2,
∴,
由旋转可得△HOB≌△,,
∴线段所扫过部分的面积为:.
故答案为:.
18.
【分析】在直角△ABC中,BC=2,AC=,根据勾股定理得到AB的长为4.求出∠CAB、∠CBA,顶点A运动到点A″的位置时,AB扫过的面积=扇形 BAA′+圆环BJKB′′+ 圆环 A′KLA′′-弓形BM,根据扇形的面积公式可以进行计算.
解:∵在Rt△ACB中,BC=2,AC=,
∴由勾股定理得:AB=4,
∴AB=2BC,
∴∠CAB=30°,∠CBA=60°,
∴∠ABA′=120°,∠A″C″A′=90°,
过点C′′作C′′F⊥A′B,作C′′F′⊥A′′B′′,垂足分别是F,F′,
∴C′′F′=C′′F=,
∴AB扫过的面积=扇形BAA′+圆环BJKB′′+圆环A′KLA′′-弓形BM,
=
=
=
故答案为:.
三、解答题
19.
解:(1)作A1H⊥AB于H,连接BD,BD1,则四边形ADA1H是矩形.
∴AD=HA1=n=1,
在Rt△A1HB中,∵BA1=BA=m=2,
∴BA1=2HA1,
∴∠ABA1=30°,
∴旋转角为30°,
∵BD=,
∴D到点D1所经过路径的长度=
(2)∵△BCE∽△BA2D2,
∴,
∴CE=
∵-1
∴,
∴A1C= ,
∴BH=A1C= ,
∴m2-n2=6 ,
∴m4-m2n2=6n4,
1-=6 ,
∴(负根已经舍弃).
20.
解:(1)①如图1,为圆的切线.
由题意可得,,.
,
②如图1,连结,交BP于点Q.则有.
在中,.
在中,,
.
(2)如图2.连结OD.设.
∵点D为的中点.
.
由题意可得,.
又
,,解得.
.
21.
解:是直径
是的平分线
在中,
,证明如下
延长到,使,连接
又
为等腰直角三角形
连接
点为的内心
所以点在以为弦,并且所对的圆周角为的两段劣弧上(分左右两种情况);
设所在圆的圆心
弧的长为=
点经过路径长为=
22.
解:(1)①∵四边形ABCD是正方形,
∴AB=DA=CD,∠BAE=∠ADF=90°,
∵DE=CF,
∴AE=DF,
∴△ABE≌△DAF,
∴∠ABE=∠DAF,
∵∠ABE+∠AEB=90°,
∴∠DAF+∠AEB=90°,
∴∠AHE=90°,
∴AF⊥BE;
②点H运动路径画图如下,
∵∠AHB=90°,且AB是定长,
∴点H在以AB为直径的圆上,且H可以与M,B重合即运动路径是一段优弧,
设AB的中点为点O,连接BD,设BD 的中点为点M,连接OM
∴∠BOM=90°,
∵AB=4,
∴圆的半径为2,
∴弧长为=3π;
(2)①根据圆的性质,当O,H,D共线,且H在O,D之间时最短,当H与点G重合时,最短,
∵AD=4,AO=2,
∴DO==;
∴DH=DO-OG=,
故答案为:.
②根据圆的性质,当O,H,D共线,且H在O,D之外时最大,当H与点Q重合时,最大,
∵AD=4,AO=2,
∴DO==;
∴DH=DO+OQ=,
故答案为:.
23.
解:(1) ∵OM=ON,∠MON=60°,∴△MON是等边三角形,∴MN=OM=ON=2.
(2) 作OH⊥MN于H点,∴.在Rt△OHN中, ,
∴.,
∴,即.
(3) 令,即,∴.当时,;
当时,;当时,.
24.
解:(1)∵∠A的度数为α,
∴∠COB=2∠A=2α,
(2)当∠ABC=90°时,AC为⊙O的直径,
∵CD∥AB,
∴∠DCB=180°﹣90°=90,
∴BD为⊙O的直径,
∴P与圆心O重合,
∵PQ∥AB交于Q,
∴OQ⊥BC,
∴CQ=BQ,
∵AB=8,
∴OQ=AB=4,
设⊙O的半径为r,
∵△OBC的周长为16,
∴CQ=8﹣r,
∴(8﹣r)2+42=r2,
解得r=5,CB=6,
∴阴影部分面积=;
(3)∵CD∥AB∥PQ,
∴△BPQ∽△BDC,△CPQ∽△CAB,
∴,
∴,
∵PQ=2,
∴,
∴=2.
一、单选题
1.如图,的半径为3,是的弦,直径,,则的长为( )
A. B. C. D.
2.如图,在中,,将绕点按逆时针方向旋转后得到,则阴影部分面积为( )
A.8 B.9 C.16 D.18
3.如图,∠MON=40°,以O为圆心,4为半径作弧交OM于点A,交ON于点B,分别以点A,B为圆心,大于的长为半径画弧,两弧在∠MON的内部相交于点C,画射线OC交于点D,E为OA上一动点,连接BE,DE,则阴影部分周长的最小值为( )
A. B. C. D.
4.如图,矩形ABCD中,,以AB为直径作,与CD相交于E,F两点,则图中阴影部分的面积是( )
A. B. C. D.
5.如图,把半径为3的⊙O沿弦AB,AC折叠,使和都经过圆心O,则阴影部分的面积为( ).
A. B. C. D.
6.如图,在中,,,是的平分线,经过,两点的圆的圆心恰好落在上,分别与、相交于点、.若圆半径为2.则阴影部分面积( ).
A. B. C. D.
7.如图,正方形ABCD的边长为4,分别以正方形的三边为直径在正方形内部作半圆,则阴影部分的面积之和是( )
A.8 B.4 C.16π D.4π
8.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A. B. C. D.
9.如图,矩形A′B′C′D′是由矩形ABCD绕C点顺时针旋转而得,且点A、C、D′在同一条直线上,在Rt△ABC中,若AB=2,AD=2,则对角线AC旋转所扫过的扇形面积为( )
A. B. C. D.
10.如图,在矩形中,为对角线,,,以为圆心,长为半径画弧,交于点,交于点,则阴影部分的面积为( )
A. B. C. D.
二、填空题
11.如图,在矩形ABCD中,点O在BC边上,,以O为圆心,OB的长为半径画弧,这条弧恰好经过点D,且交AD于E点,则BE弧的长为_______.
12.如图,矩形中,,,以为直径的半圆与相切于点,连接,则阴影部分的面积为__.(结果保留
13.如图,在边长为的菱形中,,点分别是上的动点,且与交于点.当点从点运动到点时,则点的运动路径长为_____.
14.一个扇形的弧长为 6π,圆心角为 120°,则此扇形的面积为_______.
15.如图,正方形ABCD,边长为4,点P和点Q在正方形的边上运动,且PQ=4,若点P从点B出发沿B→C→D→A的路线向点A运动,到点A停止运动;点Q从点A出发,沿A→B→C→D的路线向点D运动,到达点D停止运动.它们同时出发,且运动速度相同,则在运动过程中PQ的中点O所经过的路径长为_____.
16.如图,在菱形中,是对角线,,⊙O与边相切于点,则图中阴影部分的面积为_______.
17.如图,等边中,,、分别为边、的三等分点,,,将绕点顺时针旋转100°到的位置,则整个旋转过程中线段所扫过部分的面积为______.
18.如图,把一个直角三角形ABC的斜边AB放在直线上,按顺时针方向在上转动两次,使它转到△A″B″C″的位置.设BC=2,AC=,则顶点A运动到点A″的位置时,线段AB扫过的图形面积是__.
三、解答题
19.如图,矩形ABCD中,AB=m,BC=n,将此矩形绕点B顺时针方向旋转θ(0°<θ<90°)得到矩形A1BC1D1,点A1在边CD上.
(1)若m=2,n=1,求在旋转过程中,点D到点D1所经过路径的长度;
(2)将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2,点D2在BC的延长线上,设边A2B与CD交于点E,若=﹣1,求的值.
20.在扇形中,半径,点P在OA上,连结PB,将沿PB折叠得到.
(1)如图1,若,且与所在的圆相切于点B.
①求的度数.
②求AP的长.
(2)如图2,与相交于点D,若点D为的中点,且,求的长.
21.如图,的直径为,弦为的平分线交于点.
(1)求的长;
(2)试探究之间的等量关系,并证明你的结论;
(3)连接为半圆上任意一点,过点作于点,设的内心为,当点在半圆上从点运动到点时,求内心所经过的路径长
22.如图,正方形ABCD的边长为4cm,点E、F分别从点D和点C出发,沿着射线DA、射线CD运动,且DE=CF,直线AF、直线BE交于H点.
(1)当点E从点D向点A运动的过程中:
①求证:AF⊥BE;
②在图中画出点H运动路径并求出点H运动的路径长;
(2)在整个运动过程中:
①线段DH长度的最小值为______.
②线段DH长度的最大值为_________ .
23.如图,在半径为2的⊙O中,点Q为优弧MN的中点,圆心角∠MON=60°,在弧QN上有一动点P,且点P到弦MN所在直线的距离为x.
(1) 求弦MN的长;
(2) 试求阴影部分面积y与x的函数关系式,并写出自变量x的取值范围;
(3) 试分析比较,阴影部分面积y与的大小关系.
24.已知:如图,BC为⊙O的弦,点A为⊙O上一个动点,△OBC的周长为16.过C作CD∥AB交⊙O于D,BD与AC相交于点P,过点P作PQ∥AB交于Q,设∠A的度数为α.
(1)如图1,求∠COB的度数(用含α的式子表示);
(2)如图2,若∠ABC=90°时,AB=8,求阴影部分面积(用含α的式子表示);
(3)如图1,当PQ=2,求的值.
答案
一、单选题
1.C
【分析】连接OC,利用垂径定理以及圆心角与圆周角的关系求出;再利用弧长公式即可求出的长.
解:连接OC
(同弧所对的圆心角是圆周角的2倍)
∵直径
∴=(垂径定理)
∴
故选C
2.C
【分析】旋转后△ABC≌△A1BC1,则阴影部分面积=S△ABA1+S△A1BC1-S△ABC.
解:∵在△ABC中,AB=6,旋转后△ABC≌△A1BC1,
∴A1B=AB=6,
∴△A1BA是等腰三角形,∠A1BA=30°,
∴S△ABA1==9,
∵阴影部分面积=S△ABA1+S△A1BC1-S△ABC,
∴阴影部分面积=9.
3.A
【分析】利用作图可知OA=OB=OD=4,∠BOD=∠DOA=20°,即可求出的长度,作D点关于OM的对称点F,连接EF、OF、BF,根据∠FOA=∠DOA=20°,OF=OD=OB,ED=EF,得到∠BOF=60°,得到△OBF是等边三角形,则有BE+DE=BE+EF的最小值为BF=4(B、E、F三点在同一直线上),则问题得解.
解:作D点关于OM的对称点F,连接EF、OF、BF,如图所示:
根据题条件可知,∠BOD=∠DOA=20°,
∴,
∵D、F关于OM对称,
∴∠FOA=∠DOA=20°,OF=OD=OB,ED=EF,
∴∠BOF=60°,
∴△OBF是等边三角形,BF=OB=4,
∵DE=EF,
∴BE+DE=BE+EF,
∵的长度为定值,
∴要想求阴影部分的周长最小即求BE+DE的最小值,
又∵BE+DE=BE+EF,
∴要求BE+EF的最小值,
由图可知当B、E、F三点在同一直线上时,BE+EF=BF,此时有最小值,
∵△OBF是等边三角形,BF=OB=4,
∴BE+EF=BF=4此时最小,
∴阴影部分的周长最小值为:,
故选:A.
4.D
【分析】连接OF、OE,过点O作OH⊥CD于点H,利用勾股定理求出FH=1,得到∠FOH=45°,根据等腰三角形的三线合一的性质得到EF=2FH=2,∠EOF=90°,再利用扇形EOF的面积减去△EOF的面积即可得到答案.
解:如图,连接OF、OE,过点O作OH⊥CD于点H,
∵OF=AB=,OH=BC=1,∠OHF=90°,
∴,
∴FH=OH,
∴∠FOH=45°,
∵OF=OE,
∴EF=2FH=2,∠EOF=90°,
∴阴影部分的面积是.
故选:D
5.C
【分析】阴影部分面积是不规则图形,因此首先连接OA,OB,OC,将不规则图形转化为规则图形求面积.求扇形面积需知道圆心角的度数,因此作圆心O关于弦AB,AC的对称点,即可得到OE=OA,即可得到∠AOC=∠AOB=∠BOC=120°,从而求出扇形BOC的面积即阴影部分面积.
解:如图,连接OA,OB,OC,并做O点关于AC的对称点D点,连接OD,叫AC于点E.
∵OA=OB=OC,
∴,
∴,
∵O点、D点关于AC的对称,
∴OE=DE=1,
∴OE=OA=OC,
∴∠OCE=∠OAE =30°
∴∠AOC=120°
同理可得∠AOB=120°,
∴∠BOC=120°,
∴,
故选C.
6.C
【分析】连接OD,OF.首先证明OD∥AC,推出S阴=S扇形OFA,再证明△AOF是等边三角形即可解决问题.
解:连接OD,OF.
∵AD是∠BAC的平分线,
∴∠DAB=∠DAC,
∵OD=OA,
∴∠ODA=∠OAD,
∴∠ODA=∠DAC,
∴OD∥AC,
∴∠ODB=∠C=90°,
∴S△AFD=S△OFA,
∴S阴=S扇形OFA,
∵OD=OA=2,AB=6,
∴OB=4,
∴OB=2OD,
∴∠B=30°,
∴∠A=60°,
∵OF=OA,
∴△AOF是等边三角形,
∴∠AOF=60°,
∴S阴=S扇形OFA=.
故选:C.
7.A
【分析】先判断出两半圆交点为正方形的中心,连接OA,OD,则可得出所产生的四个小弓形的面积相等,先得出2个小弓形的面积,即可求阴影部分面积.
解:由题意,易知两半圆的交点即为正方形的中心,设此点为O,连接AO,DO,
则图中的四个小弓形的面积相等,
∵两个小弓形面积=S半圆AOD-S△AOD=S半圆AOD-S正方形ABCD,
又正方形ABCD的边长为4,得各半圆的半径为2,
∴两个小弓形面积=×π×22﹣×4×4=2π﹣4,
∴S阴影=2×S半圆﹣4个小弓形面积=π 22﹣2(2π﹣4)=8,
故选:A.
8.B
解:分析:连接AC,AG,由OG垂直于AB,利用垂径定理得到O为AB的中点,由G的坐标确定出OG的长,在直角三角形AOG中,由AG与OG的长,利用勾股定理求出AO的长,进而确定出AB的长,由CG+GO求出OC的长,在直角三角形AOC中,利用勾股定理求出AC的长,由CF垂直于AE,得到三角形ACF始终为直角三角形,点F的运动轨迹为以AC为直径的半径,如图中红线所示,当E位于点B时,CO⊥AE,此时F与O重合;当E位于D时,CA⊥AE,此时F与A重合,可得出当点E从点B出发顺时针运动到点D时,点F所经过的路径长,在直角三角形ACO中,利用锐角三角函数定义求出∠ACO的度数,进而确定出所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出的长.
解:连接AC,AG,
∵GO⊥AB,
∴O为AB的中点,即AO=BO=AB,
∵G(0,1),即OG=1,
∴在Rt△AOG中,根据勾股定理得:AO=,
∴AB=2AO=2,
又CO=CG+GO=2+1=3,
∴在Rt△AOC中,根据勾股定理得:AC=,
∵CF⊥AE,
∴△ACF始终是直角三角形,点F的运动轨迹为以AC为直径的半圆,
当E位于点B时,CO⊥AE,此时F与O重合;当E位于D时,CA⊥AE,此时F与A重合,
∴当点E从点B出发顺时针运动到点D时,点F所经过的路径长,
在Rt△ACO中,tan∠ACO=,
∴∠ACO=30°,
∴度数为60°,
∵直径AC=2,
∴的长为,
则当点E从点B出发顺时针运动到点D时,点F所经过的路径长.
故选B.
9.A
解:根据题意得:∠ACB=30°,则∠A′CB′=30°,则∠ACA′=90°+30°=120°,根 据勾股定理可得AC=4,则S=.
10.D
【分析】如图,连接,过作于点,此时根据直角三角形的性质求得,,再根据等边三角形判定得出为等边三角形,进而将问题转化到新的三角形之中,利用勾股定理求得,最终求阴影部分的面积转化为求解即可.
解:如下图,连接,过作于点,
在矩形中,
∵,, ,
∴,,
又∵,,
∴为等边三角形,
∴,,
∴,
故选:D.
二、填空题
11.
分析:连接OE,根据矩形的性质,得到∠C=90°,进而得到∠ODC=90°,然后得出等边三角形EOD,可求∠BOE=60°,再根据弧长公式求解即可.
解:连接OE
∵矩形ABCD中,BO=2CO=2
∴DO=2CO=2
∴∠ODC=30°
∴∠EDO=∠DOC=60°
∵OE=OD
∴∠EOD=60°
∴∠BOE=60°
∴BE弧的长为.
故答案为.
12.π.
【分析】如图所示,连接OE交BD于点F,利用切线的性质得OD=2,OE⊥BC,易得四边形OECD为正方形,再证△EFB≌△OFD,即可将阴影部分面积转化为扇形OED的面积,最后利用扇形面积公式求解即可得出答案.
解:如图所示,连接OE交BD于点F,
∵以AD为直径的半圆O与BC相切于点E,
∴OD=2,OE⊥BC,
∴OE=OD=2,
在矩形中,
∵
∴四边形OECD为正方形,
∴CE=OD=2,
∴BE=BC-CE=2,
∴BE=DO,
∵AD//BC,
∴
∴△EFB≌△OFD,
∴阴影部分的面积= .
故答案为π.
13.
【分析】根据题意证得,推出∠BPE =60,∠BPD =120,得到C、B、P、D四点共圆,知点的运动路径长为的长,利用弧长公式即可求解.
解:连接BD,
∵菱形中,,
∴∠C=∠A=60,AB=BC=CD=AD,
∴△ABD和△CBD都为等边三角形,
∴BD=AD,∠BDF=∠DAE=60,
∵DF=AE,
∴,
∴∠DBF=∠ADE,
∵∠BPE=∠BDP+∠DBF =∠BDP+∠ADE=∠BDF =60,
∴∠BPD=180-∠BPE=120,
∵∠C=60,
∴∠C+∠BPD =180,
∴C、B、P、D四点共圆,即⊙O是的外接圆,
∴当点从点运动到点时,则点的运动路径长为的长,
∴∠BOD =2∠BCD =120,
作OG⊥BD于G,
根据垂径定理得:BG=GD=BD=,∠BOG =∠BOD =60,
∵,即,
∴,
从而点的路径长为.
14.27π
【分析】先根据弧长公式求出扇形的半径,再根据扇形的面积公式求解即可.
解:设扇形的半径为r,则
解得:
∴扇形的面积
故答案为:.
15.
解:画出点O运动的轨迹,如图虚线部分,
则点P从B到A的运动过程中,PQ的中点O所经过的路线长等于3π,
故答案为:3π.
16.
【分析】连接OD,先求出等边三角形OAB的面积,再求出扇形的面积,即可求出阴影部分的面积.
解:如图,连接OD,
∵AB是切线,则OD⊥AB,
在菱形中,
∴,
∴△AOB是等边三角形,
∴∠AOB=∠A=60°,
∴OD=,
∴,
∴扇形的面积为:,
∴阴影部分的面积为:;
故答案为:.
17.
【分析】连接BH、,过点H作HMBC于点M,根据等边三角形的性质和已知条件可求得AH=AO=2,HC=OB=4,在Rt△HCM中,求得CM=2,HM=2,在Rt△HBM中,求得,由旋转可得△HOB≌△,,即可得线段所扫过部分的面积为,由此即可求解.
解:连接BH、,过点H作HMBC于点M,
∵为等边三角形,,
∴,∠C=60°,
∵,,
∴AH=AO=2,
∴HC=OB=4,
在Rt△HCM中,∠C=60°,HC=4,
∴CM=2,HM=2,
∵BC=6,
∴BM=4,
在Rt△HBM中,BM=4,HM=2,
∴,
由旋转可得△HOB≌△,,
∴线段所扫过部分的面积为:.
故答案为:.
18.
【分析】在直角△ABC中,BC=2,AC=,根据勾股定理得到AB的长为4.求出∠CAB、∠CBA,顶点A运动到点A″的位置时,AB扫过的面积=扇形 BAA′+圆环BJKB′′+ 圆环 A′KLA′′-弓形BM,根据扇形的面积公式可以进行计算.
解:∵在Rt△ACB中,BC=2,AC=,
∴由勾股定理得:AB=4,
∴AB=2BC,
∴∠CAB=30°,∠CBA=60°,
∴∠ABA′=120°,∠A″C″A′=90°,
过点C′′作C′′F⊥A′B,作C′′F′⊥A′′B′′,垂足分别是F,F′,
∴C′′F′=C′′F=,
∴AB扫过的面积=扇形BAA′+圆环BJKB′′+圆环A′KLA′′-弓形BM,
=
=
=
故答案为:.
三、解答题
19.
解:(1)作A1H⊥AB于H,连接BD,BD1,则四边形ADA1H是矩形.
∴AD=HA1=n=1,
在Rt△A1HB中,∵BA1=BA=m=2,
∴BA1=2HA1,
∴∠ABA1=30°,
∴旋转角为30°,
∵BD=,
∴D到点D1所经过路径的长度=
(2)∵△BCE∽△BA2D2,
∴,
∴CE=
∵-1
∴,
∴A1C= ,
∴BH=A1C= ,
∴m2-n2=6 ,
∴m4-m2n2=6n4,
1-=6 ,
∴(负根已经舍弃).
20.
解:(1)①如图1,为圆的切线.
由题意可得,,.
,
②如图1,连结,交BP于点Q.则有.
在中,.
在中,,
.
(2)如图2.连结OD.设.
∵点D为的中点.
.
由题意可得,.
又
,,解得.
.
21.
解:是直径
是的平分线
在中,
,证明如下
延长到,使,连接
又
为等腰直角三角形
连接
点为的内心
所以点在以为弦,并且所对的圆周角为的两段劣弧上(分左右两种情况);
设所在圆的圆心
弧的长为=
点经过路径长为=
22.
解:(1)①∵四边形ABCD是正方形,
∴AB=DA=CD,∠BAE=∠ADF=90°,
∵DE=CF,
∴AE=DF,
∴△ABE≌△DAF,
∴∠ABE=∠DAF,
∵∠ABE+∠AEB=90°,
∴∠DAF+∠AEB=90°,
∴∠AHE=90°,
∴AF⊥BE;
②点H运动路径画图如下,
∵∠AHB=90°,且AB是定长,
∴点H在以AB为直径的圆上,且H可以与M,B重合即运动路径是一段优弧,
设AB的中点为点O,连接BD,设BD 的中点为点M,连接OM
∴∠BOM=90°,
∵AB=4,
∴圆的半径为2,
∴弧长为=3π;
(2)①根据圆的性质,当O,H,D共线,且H在O,D之间时最短,当H与点G重合时,最短,
∵AD=4,AO=2,
∴DO==;
∴DH=DO-OG=,
故答案为:.
②根据圆的性质,当O,H,D共线,且H在O,D之外时最大,当H与点Q重合时,最大,
∵AD=4,AO=2,
∴DO==;
∴DH=DO+OQ=,
故答案为:.
23.
解:(1) ∵OM=ON,∠MON=60°,∴△MON是等边三角形,∴MN=OM=ON=2.
(2) 作OH⊥MN于H点,∴.在Rt△OHN中, ,
∴.,
∴,即.
(3) 令,即,∴.当时,;
当时,;当时,.
24.
解:(1)∵∠A的度数为α,
∴∠COB=2∠A=2α,
(2)当∠ABC=90°时,AC为⊙O的直径,
∵CD∥AB,
∴∠DCB=180°﹣90°=90,
∴BD为⊙O的直径,
∴P与圆心O重合,
∵PQ∥AB交于Q,
∴OQ⊥BC,
∴CQ=BQ,
∵AB=8,
∴OQ=AB=4,
设⊙O的半径为r,
∵△OBC的周长为16,
∴CQ=8﹣r,
∴(8﹣r)2+42=r2,
解得r=5,CB=6,
∴阴影部分面积=;
(3)∵CD∥AB∥PQ,
∴△BPQ∽△BDC,△CPQ∽△CAB,
∴,
∴,
∵PQ=2,
∴,
∴=2.
同课章节目录
