九年级数学上册试题 3.8 弧长及扇形的面积-浙教版(含解析)
文档属性
| 名称 | 九年级数学上册试题 3.8 弧长及扇形的面积-浙教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 07:23:41 | ||
图片预览



文档简介
3.8 弧长及扇形的面积
一、单选题
1.已知扇形的半径为6,圆心角为20°,则扇形的面积为( )
A. B. C. D.
2.如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )
A.6π B.2π C.π D.π
3.若扇形的圆心角为,弧长为,则该扇形的半径为( )
A. B.6 C.12 D.
4.如果一弧长是其所在圆周长的,那么这条弧长所对的圆心角为( )
A.15度 B.16度 C.20度 D.24度
5.如图是边长为1的正方形组成的网格,△ABC的顶点都在格点上,将△ABC绕点C逆时针旋转60°,则顶点B所经过的路径长为( )
A. B. C. D.
6.如图,Rt△ABC中,∠ACB=90°,AC=BC=2,在以AB的中点O为坐标原点、AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴正半轴上的A′处,则图中阴影部分面积为( )
A.-2 B. C. D.-2
7.如图,在扇形中,∠,,则阴影部分的面积是( )
A. B.
C. D.
8.如图,正方形中,分别以,为圆心,以正方形的边长为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的面积为( )
A. B. C. D.
9.如图,在边长为6的正方形中,以为直径画半圆,则阴影部分的面积是( )
A.9 B.6 C.3 D.12
10.如图,一扇形纸扇完全打开后,外侧两条竹条AB、AC的夹角为120°,AB长为30cm,AD=10cm,贴纸部分的面积为( )
A.πcm2 B.πcm2 C.800πcm2 D.500πcm2
二、填空题
11.已知扇形的圆心角的度数是120 ,半径为9,则此扇形弧长是______.
12.在活动课上,“雄鹰组”用含30°角的直角三角尺设计风车.如图,∠C=90°,∠ABC=30°,AC=2,将直角三角尺绕点A逆时针旋转得到△AB′C′,使点C′落在AB边上,以此方法做下去……则B点通过一次旋转至B′所经过的路径长为 _____.(结果保留π)
13.如图,与轴相切,与轴相交于点,.
(1)的半径______;
(2)扇形的面积为______.
14.如图,将△ABC绕点C顺时针旋转120°得到△A'B'C,已知AC=3,BC=2,则=__________;线段AB扫过的图形(阴影部分)的面积为__________.
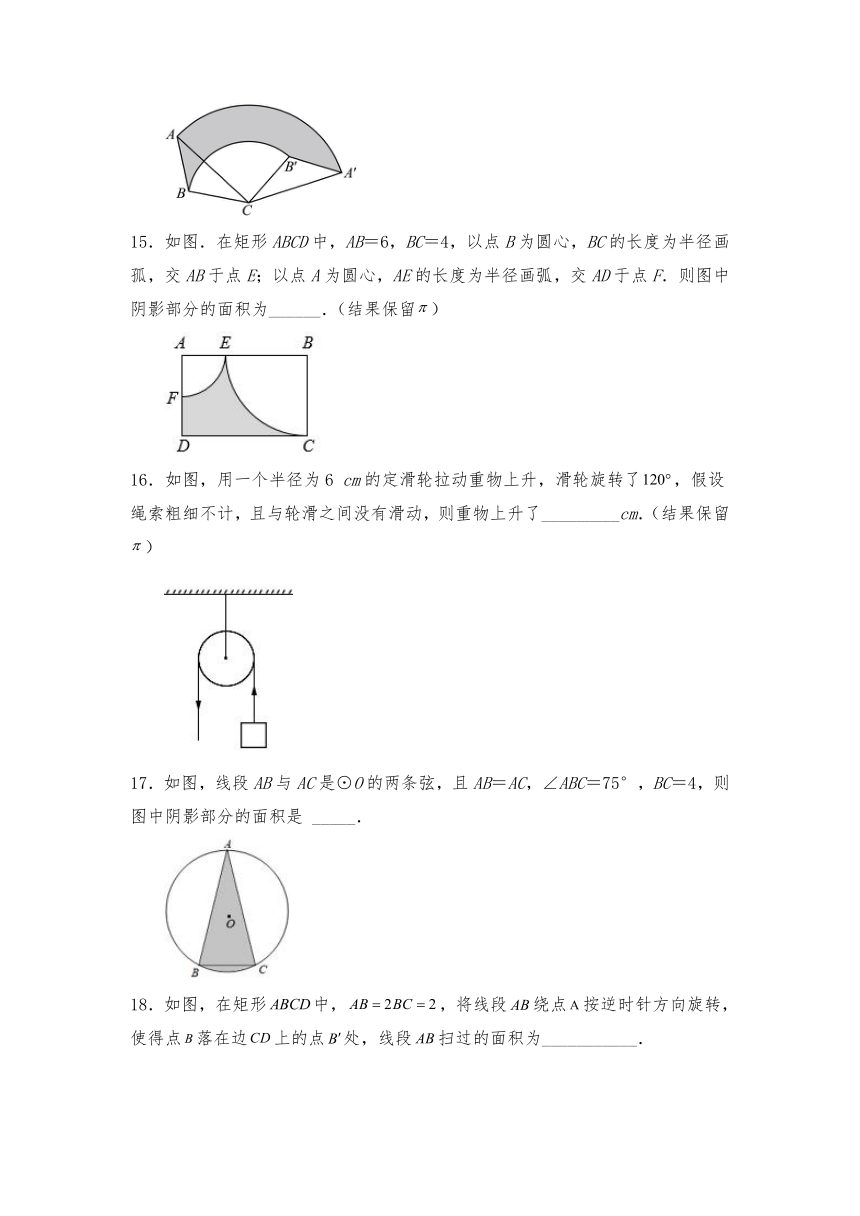
15.如图.在矩形ABCD中,AB=6,BC=4,以点B为圆心,BC的长度为半径画孤,交AB于点E;以点A为圆心,AE的长度为半径画弧,交AD于点F.则图中阴影部分的面积为______.(结果保留)
16.如图,用一个半径为6 cm的定滑轮拉动重物上升,滑轮旋转了,假设绳索粗细不计,且与轮滑之间没有滑动,则重物上升了_________cm.(结果保留)
17.如图,线段AB与AC是⊙O的两条弦,且AB=AC,∠ABC=75°,BC=4,则图中阴影部分的面积是 _____.
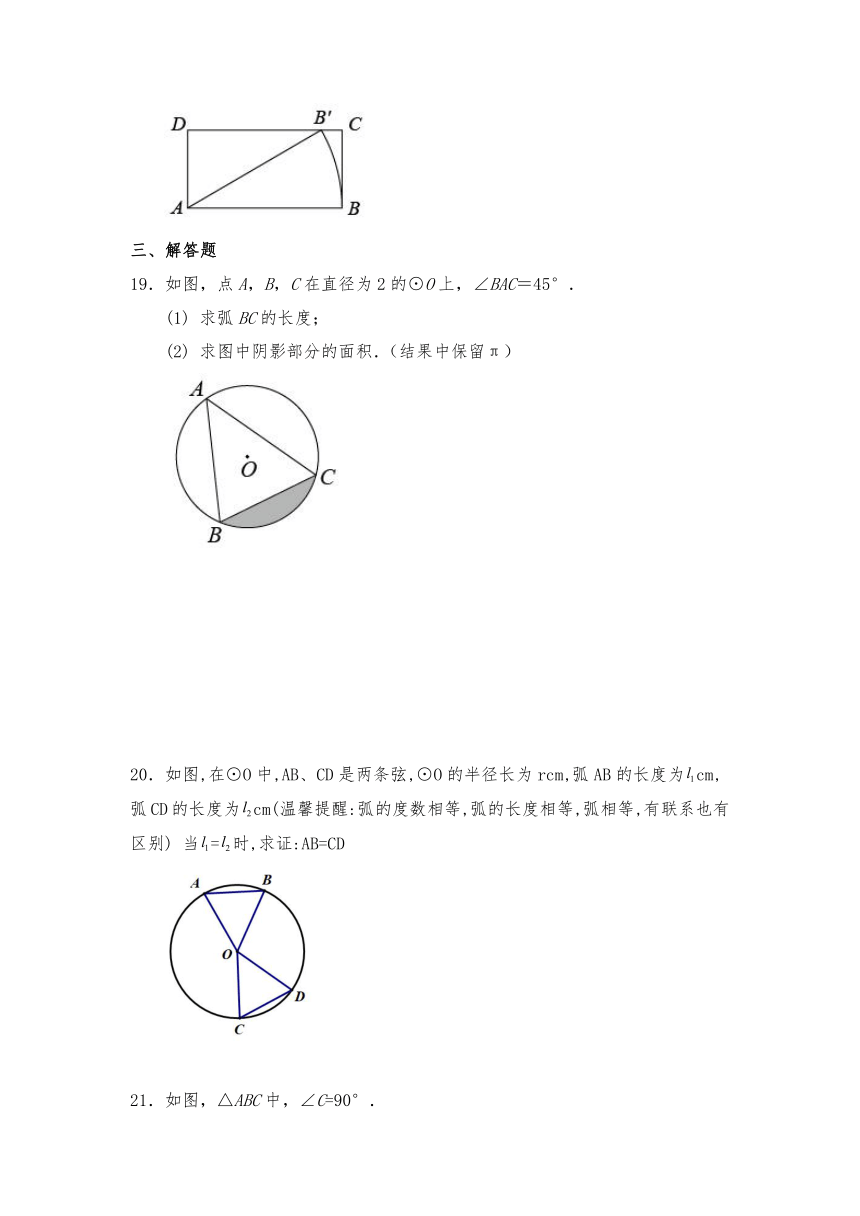
18.如图,在矩形中,,将线段绕点按逆时针方向旋转,使得点落在边上的点处,线段扫过的面积为___________.
三、解答题
19.如图,点A,B,C在直径为2的⊙O上,∠BAC=45°.
(1) 求弧BC的长度;
(2) 求图中阴影部分的面积.(结果中保留π)
20.如图,在⊙O中,AB、CD是两条弦,⊙O的半径长为rcm,弧AB的长度为cm,弧CD的长度为cm(温馨提醒:弧的度数相等,弧的长度相等,弧相等,有联系也有区别) 当=时,求证:AB=CD
21.如图,△ABC中,∠C=90°.
(1) 将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1;(不写画法,保留画图痕迹)
(2) 若AB=10,BC=6,求在旋转过程中,点C运动的路径长.
22.如图,一根长的绳子,一端拴在柱子上,另一端拴着一只羊(羊只能在草地上活动),请画出羊的活动区域.
23.如图Rt△ABC中,∠C=90°,AD平分∠BAC,AD交BC于点D,点E在AB上,以AE为直径的⊙O经过点D.
(1) 求证:直线BC是⊙O的切线.
(2) 若AC=6,∠B=30°,求图中阴影部分的面积.
24.如图,在△ABC中,经过A,B两点的⊙O与边BC交于点E,圆心O在BC上,过点O作OD⊥BC交⊙O于点D,连接AD交BC于点F,且AC=FC.
(1)试判断AC与⊙O的位置关系,并说明理由;
(2)若FC=,CE=1.求图中阴影部分的面积(结果保留π).
答案
一、单选题
1.D
【分析】根据扇形的面积公式即可得.
解:扇形的半径为6,圆心角为,
扇形的面积为,
故选:D.
2.D
【分析】先根据圆周角定理求出∠BOC=2∠A=60°,求出半径OB,再根据弧长公式求出答案即可.
解:∵直径AB=6,
∴半径OB=3,
∵圆周角∠A=30°,
∴圆心角∠BOC=2∠A=60°,
∴的长是=π,
故选:D.
3.B
【分析】根据弧长公式可以求得该扇形的半径的长度.
解:根据弧长的公式,知
=6,
即该扇形的半径为6.
故选:B.
4.C
【分析】根据弧长公式和圆的周长公式的关系即可得出答案
解:∵一弧长是其所在圆周长的,
∴
∴
∴这条弧长所对的圆心角为
故选:C
5.B
【分析】先根据勾股定理计算出BC=,顶点B所经过的路径为弧,根据旋转的性质得弧所对的圆心角为60°,然后根据弧长公式求解.
解:BC==,
所以顶点B所经过的路径长=.
故选:B.
6.C
解:试题分析:阴影部分的面积等于扇形ABA′的面积+Rt△A′C′B的面积-Rt△ABC的面积-扇形BCC′的面积.
7.D
【分析】利用阴影部分的面积等于扇形面积减去的面积即可求解.
解:
=
故选D
8.B
【分析】由图可知,树叶形图案的面积是两个圆心角为90°,且半径为a的扇形的面积与正方形的面积的差,可据此求出树叶形图案的面积.
解:树叶形图案的面积为:
.
故选:B.
9.A
【分析】设AC与半圆交于点E,半圆的圆心为O,连接BE,OE,证明BE=CE,得到弓形BE的面积=弓形CE的面积,则.
解:设AC与半圆交于点E,半圆的圆心为O,连接BE,OE,
∵四边形ABCD是正方形,
∴∠OCE=45°,
∵OE=OC,
∴∠OEC=∠OCE=45°,
∴∠EOC=90°,
∴OE垂直平分BC,
∴BE=CE,
∴弓形BE的面积=弓形CE的面积,
∴,
故选A.
10.A
【分析】贴纸部分的面积为大扇形面积减去小扇形面积,根据扇形面积公式解答.
解:贴纸部分的面积为(cm2),
故选:A.
二、填空题
11.6π
【分析】根据扇形的弧长公式计算即可.
解:∵圆心角的度数是120 ,半径为9,
∴扇形的弧长为:.
故答案为:6π.
12.
【分析】根据题意,点B所经过的路径是圆弧,根据直角三角形30°角所对的边等于斜边的一半,易知AB=4,结合旋转的性质可知∠BAB′=∠BAC=60°,,最后求出圆弧的长度即可.
解:∵∠C=90°,∠ABC=30°,AC=2,
∴AB=2AC=4,∠BAC=60°,
由旋转的性质得,∠BAB′=∠BAC=60°,
∴B点通过一次旋转至B′所经过的路径长为,
故答案为:.
13. 2; ##
【分析】作AF⊥BC,假设⊙A与x轴相切于E点,连接AE,做BD⊥AE,利用垂径定理的内容得出BF=CF,进而得出AD与半径的关系,从而得出△ABC为等边三角形,然后计算半径,再利用扇形面积公式求出即可.
解:作AF⊥BC,假设⊙A与x轴相切于E点,连接AE,BD⊥AE,
假设AE=x,图象与y轴相交于点B(0,1)、C(0,3),
∴OB=DE=1,AD=x-1,
∵AC=AB,AF⊥BC,
∴BF=CF=1,
∴AD=BF=1=x-1,
解得:x=2,
∴AB=BC=AC=2,
△ABC为等边三角形,
∴∠BAC=60°,
∴扇形BAC的面积=,
故答案为:2;.
14.
【分析】根据弧长公式可求得的长;根据图形可以得出AB扫过的图形的面积=S扇形ACA′+S△ABC-S扇形BCB′-S△A′B′C,由旋转的性质就可以得出S△ABC=S△A′B′C就可以得出AB扫过的图形的面积=S扇形ACA′-S扇形BCB′求出其值即可.
解:∵△ABC绕点C旋转120°得到△A′B′C,
∴△ABC≌△A′B′C,
∴S△ABC=S△A′B′C,∠BCB′=∠ACA′=120°.
∴的长为:2π;
∵AB扫过的图形的面积=S扇形ACA′+S△ABC-S扇形BCB′-S△A′B′C,
∴AB扫过的图形的面积=S扇形ACA′-S扇形BCB′,
∴AB扫过的图形的面积= .
故答案为:2π;.
15.
【分析】利用分割法求解即可.
解:在矩形ABCD中AB=6,BC=4,
∴BE=BC=4,
∴AE=AB-BE=6-4=2,
∴S阴=S矩形ABCD-S扇形AEF-S扇形BEC
=6×4-
=24-5π,
故答案为:24-5π.
16.
【分析】利用题意得到重物上升的高度为定滑轮中120°所对应的弧长,然后根据弧长公式计算即可.
解:根据题意,重物的高度为
(cm).
故答案为:.
17.8
【分析】如图,连接OA,OB,OC,延长AO交BC于点H.根据S阴=S△ABC﹣S△OBC +S扇形OBC,求解即可.
解:如图,连接OA,OB,OC,延长AO交BC于点H.
∵AB=AC,
∴∠ABC=∠ACB=75°,
∴∠BAC=30°,
∴∠BOC=2∠BAC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴OB=OC=BC=4,
∴OA=4,
∵AB=AC,
∴,
∴AO⊥BC,
∴BH=CH=2,
∴OH=2,
∴AH=4+2,
∴S△ABC BC AH4×(4+2)=8+4,S△OBC4,S扇形OBC
∴S阴=S△ABC﹣S△OBC+ S扇形OBC=8.
故答案为:8.
18.
【分析】由旋转的性质可得由锐角三角函数可求从而得出由扇形面积公式即可求解.
解:
∵矩形中,
由旋转可知,
∵,
∴
∴线段AB扫过的面积
故答案为:
三、解答题
19.
解:(1)如图,连接OB,OC.
∵∠BOC=2∠A,∠A=45°,
∴∠BOC=90°,
∵⊙O的直径为2,
∴OB=OC=1,
∴;
(2)∵∠BOC=90°,
∴△BOC是直角三角形,
∵⊙O的直径为2,
∴OB=OC=1,
∴△BOC的面积为,
∵,
即S阴=S扇形OBC﹣S△OBC=.
20.
解:令∠AOB=α,∠COD=β.
∵=
∴
∵AB和CD在同圆中,r1=r2
∴α=β
∴AB=CD
21.
(1)解:点C绕点A顺时针旋转90°得点C1,点B绕点A顺时针旋转90°得点B1,连结AB1,B1C1,AC1如图,△AB1C1为所画三角形;
;
(2)解:在中,∵∠C=90°,AB=10,BC=6,
∴.
∵绕点A顺时针旋转得到,
∴.
∴点C运动的路径长为:.
22.
解:如图,
以点O为圆心,5m长的绳子为半径画弧交草地左边界于点A,交OD的延长线于点B,再以D为圆心,DB长为半径画弧交草地的右边界于点C,
则扇形AOB和扇形BDC部分即为羊的活动区域.
23.
(1)证明:连接OD,
∵AD平分∠BAC,
∴∠OAD=∠CAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODB=90°,
∴OD⊥BC,
∴直线BC是⊙O的切线;
(2)解:由∠B=30°,∠C=90°,∠ODB=90°,
得:AB=2AC=12,OB=2OD,∠AOD=120°,
∠DAC=30°,
∵OA=OD,
∴OB=2OA,
∴OA=OD=4,
由∠DAC=30°,得DC=2,
∴S阴影=S扇形OAD-S△OAD
=
=π-4.
24.
解:(1)AC与⊙O的相切,理由如下,
,
,
,
,
又,
,
OD⊥BC,
,
,
,
是半径,
是的切线,
AC与⊙O的相切;
(2)过作于,如图,
设,
,
在中
,
,
,
解得,
,
,
,
,
,
在中,
,
,
扇形,
阴影部分扇形.
一、单选题
1.已知扇形的半径为6,圆心角为20°,则扇形的面积为( )
A. B. C. D.
2.如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )
A.6π B.2π C.π D.π
3.若扇形的圆心角为,弧长为,则该扇形的半径为( )
A. B.6 C.12 D.
4.如果一弧长是其所在圆周长的,那么这条弧长所对的圆心角为( )
A.15度 B.16度 C.20度 D.24度
5.如图是边长为1的正方形组成的网格,△ABC的顶点都在格点上,将△ABC绕点C逆时针旋转60°,则顶点B所经过的路径长为( )
A. B. C. D.
6.如图,Rt△ABC中,∠ACB=90°,AC=BC=2,在以AB的中点O为坐标原点、AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴正半轴上的A′处,则图中阴影部分面积为( )
A.-2 B. C. D.-2
7.如图,在扇形中,∠,,则阴影部分的面积是( )
A. B.
C. D.
8.如图,正方形中,分别以,为圆心,以正方形的边长为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的面积为( )
A. B. C. D.
9.如图,在边长为6的正方形中,以为直径画半圆,则阴影部分的面积是( )
A.9 B.6 C.3 D.12
10.如图,一扇形纸扇完全打开后,外侧两条竹条AB、AC的夹角为120°,AB长为30cm,AD=10cm,贴纸部分的面积为( )
A.πcm2 B.πcm2 C.800πcm2 D.500πcm2
二、填空题
11.已知扇形的圆心角的度数是120 ,半径为9,则此扇形弧长是______.
12.在活动课上,“雄鹰组”用含30°角的直角三角尺设计风车.如图,∠C=90°,∠ABC=30°,AC=2,将直角三角尺绕点A逆时针旋转得到△AB′C′,使点C′落在AB边上,以此方法做下去……则B点通过一次旋转至B′所经过的路径长为 _____.(结果保留π)
13.如图,与轴相切,与轴相交于点,.
(1)的半径______;
(2)扇形的面积为______.
14.如图,将△ABC绕点C顺时针旋转120°得到△A'B'C,已知AC=3,BC=2,则=__________;线段AB扫过的图形(阴影部分)的面积为__________.
15.如图.在矩形ABCD中,AB=6,BC=4,以点B为圆心,BC的长度为半径画孤,交AB于点E;以点A为圆心,AE的长度为半径画弧,交AD于点F.则图中阴影部分的面积为______.(结果保留)
16.如图,用一个半径为6 cm的定滑轮拉动重物上升,滑轮旋转了,假设绳索粗细不计,且与轮滑之间没有滑动,则重物上升了_________cm.(结果保留)
17.如图,线段AB与AC是⊙O的两条弦,且AB=AC,∠ABC=75°,BC=4,则图中阴影部分的面积是 _____.
18.如图,在矩形中,,将线段绕点按逆时针方向旋转,使得点落在边上的点处,线段扫过的面积为___________.
三、解答题
19.如图,点A,B,C在直径为2的⊙O上,∠BAC=45°.
(1) 求弧BC的长度;
(2) 求图中阴影部分的面积.(结果中保留π)
20.如图,在⊙O中,AB、CD是两条弦,⊙O的半径长为rcm,弧AB的长度为cm,弧CD的长度为cm(温馨提醒:弧的度数相等,弧的长度相等,弧相等,有联系也有区别) 当=时,求证:AB=CD
21.如图,△ABC中,∠C=90°.
(1) 将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1;(不写画法,保留画图痕迹)
(2) 若AB=10,BC=6,求在旋转过程中,点C运动的路径长.
22.如图,一根长的绳子,一端拴在柱子上,另一端拴着一只羊(羊只能在草地上活动),请画出羊的活动区域.
23.如图Rt△ABC中,∠C=90°,AD平分∠BAC,AD交BC于点D,点E在AB上,以AE为直径的⊙O经过点D.
(1) 求证:直线BC是⊙O的切线.
(2) 若AC=6,∠B=30°,求图中阴影部分的面积.
24.如图,在△ABC中,经过A,B两点的⊙O与边BC交于点E,圆心O在BC上,过点O作OD⊥BC交⊙O于点D,连接AD交BC于点F,且AC=FC.
(1)试判断AC与⊙O的位置关系,并说明理由;
(2)若FC=,CE=1.求图中阴影部分的面积(结果保留π).
答案
一、单选题
1.D
【分析】根据扇形的面积公式即可得.
解:扇形的半径为6,圆心角为,
扇形的面积为,
故选:D.
2.D
【分析】先根据圆周角定理求出∠BOC=2∠A=60°,求出半径OB,再根据弧长公式求出答案即可.
解:∵直径AB=6,
∴半径OB=3,
∵圆周角∠A=30°,
∴圆心角∠BOC=2∠A=60°,
∴的长是=π,
故选:D.
3.B
【分析】根据弧长公式可以求得该扇形的半径的长度.
解:根据弧长的公式,知
=6,
即该扇形的半径为6.
故选:B.
4.C
【分析】根据弧长公式和圆的周长公式的关系即可得出答案
解:∵一弧长是其所在圆周长的,
∴
∴
∴这条弧长所对的圆心角为
故选:C
5.B
【分析】先根据勾股定理计算出BC=,顶点B所经过的路径为弧,根据旋转的性质得弧所对的圆心角为60°,然后根据弧长公式求解.
解:BC==,
所以顶点B所经过的路径长=.
故选:B.
6.C
解:试题分析:阴影部分的面积等于扇形ABA′的面积+Rt△A′C′B的面积-Rt△ABC的面积-扇形BCC′的面积.
7.D
【分析】利用阴影部分的面积等于扇形面积减去的面积即可求解.
解:
=
故选D
8.B
【分析】由图可知,树叶形图案的面积是两个圆心角为90°,且半径为a的扇形的面积与正方形的面积的差,可据此求出树叶形图案的面积.
解:树叶形图案的面积为:
.
故选:B.
9.A
【分析】设AC与半圆交于点E,半圆的圆心为O,连接BE,OE,证明BE=CE,得到弓形BE的面积=弓形CE的面积,则.
解:设AC与半圆交于点E,半圆的圆心为O,连接BE,OE,
∵四边形ABCD是正方形,
∴∠OCE=45°,
∵OE=OC,
∴∠OEC=∠OCE=45°,
∴∠EOC=90°,
∴OE垂直平分BC,
∴BE=CE,
∴弓形BE的面积=弓形CE的面积,
∴,
故选A.
10.A
【分析】贴纸部分的面积为大扇形面积减去小扇形面积,根据扇形面积公式解答.
解:贴纸部分的面积为(cm2),
故选:A.
二、填空题
11.6π
【分析】根据扇形的弧长公式计算即可.
解:∵圆心角的度数是120 ,半径为9,
∴扇形的弧长为:.
故答案为:6π.
12.
【分析】根据题意,点B所经过的路径是圆弧,根据直角三角形30°角所对的边等于斜边的一半,易知AB=4,结合旋转的性质可知∠BAB′=∠BAC=60°,,最后求出圆弧的长度即可.
解:∵∠C=90°,∠ABC=30°,AC=2,
∴AB=2AC=4,∠BAC=60°,
由旋转的性质得,∠BAB′=∠BAC=60°,
∴B点通过一次旋转至B′所经过的路径长为,
故答案为:.
13. 2; ##
【分析】作AF⊥BC,假设⊙A与x轴相切于E点,连接AE,做BD⊥AE,利用垂径定理的内容得出BF=CF,进而得出AD与半径的关系,从而得出△ABC为等边三角形,然后计算半径,再利用扇形面积公式求出即可.
解:作AF⊥BC,假设⊙A与x轴相切于E点,连接AE,BD⊥AE,
假设AE=x,图象与y轴相交于点B(0,1)、C(0,3),
∴OB=DE=1,AD=x-1,
∵AC=AB,AF⊥BC,
∴BF=CF=1,
∴AD=BF=1=x-1,
解得:x=2,
∴AB=BC=AC=2,
△ABC为等边三角形,
∴∠BAC=60°,
∴扇形BAC的面积=,
故答案为:2;.
14.
【分析】根据弧长公式可求得的长;根据图形可以得出AB扫过的图形的面积=S扇形ACA′+S△ABC-S扇形BCB′-S△A′B′C,由旋转的性质就可以得出S△ABC=S△A′B′C就可以得出AB扫过的图形的面积=S扇形ACA′-S扇形BCB′求出其值即可.
解:∵△ABC绕点C旋转120°得到△A′B′C,
∴△ABC≌△A′B′C,
∴S△ABC=S△A′B′C,∠BCB′=∠ACA′=120°.
∴的长为:2π;
∵AB扫过的图形的面积=S扇形ACA′+S△ABC-S扇形BCB′-S△A′B′C,
∴AB扫过的图形的面积=S扇形ACA′-S扇形BCB′,
∴AB扫过的图形的面积= .
故答案为:2π;.
15.
【分析】利用分割法求解即可.
解:在矩形ABCD中AB=6,BC=4,
∴BE=BC=4,
∴AE=AB-BE=6-4=2,
∴S阴=S矩形ABCD-S扇形AEF-S扇形BEC
=6×4-
=24-5π,
故答案为:24-5π.
16.
【分析】利用题意得到重物上升的高度为定滑轮中120°所对应的弧长,然后根据弧长公式计算即可.
解:根据题意,重物的高度为
(cm).
故答案为:.
17.8
【分析】如图,连接OA,OB,OC,延长AO交BC于点H.根据S阴=S△ABC﹣S△OBC +S扇形OBC,求解即可.
解:如图,连接OA,OB,OC,延长AO交BC于点H.
∵AB=AC,
∴∠ABC=∠ACB=75°,
∴∠BAC=30°,
∴∠BOC=2∠BAC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴OB=OC=BC=4,
∴OA=4,
∵AB=AC,
∴,
∴AO⊥BC,
∴BH=CH=2,
∴OH=2,
∴AH=4+2,
∴S△ABC BC AH4×(4+2)=8+4,S△OBC4,S扇形OBC
∴S阴=S△ABC﹣S△OBC+ S扇形OBC=8.
故答案为:8.
18.
【分析】由旋转的性质可得由锐角三角函数可求从而得出由扇形面积公式即可求解.
解:
∵矩形中,
由旋转可知,
∵,
∴
∴线段AB扫过的面积
故答案为:
三、解答题
19.
解:(1)如图,连接OB,OC.
∵∠BOC=2∠A,∠A=45°,
∴∠BOC=90°,
∵⊙O的直径为2,
∴OB=OC=1,
∴;
(2)∵∠BOC=90°,
∴△BOC是直角三角形,
∵⊙O的直径为2,
∴OB=OC=1,
∴△BOC的面积为,
∵,
即S阴=S扇形OBC﹣S△OBC=.
20.
解:令∠AOB=α,∠COD=β.
∵=
∴
∵AB和CD在同圆中,r1=r2
∴α=β
∴AB=CD
21.
(1)解:点C绕点A顺时针旋转90°得点C1,点B绕点A顺时针旋转90°得点B1,连结AB1,B1C1,AC1如图,△AB1C1为所画三角形;
;
(2)解:在中,∵∠C=90°,AB=10,BC=6,
∴.
∵绕点A顺时针旋转得到,
∴.
∴点C运动的路径长为:.
22.
解:如图,
以点O为圆心,5m长的绳子为半径画弧交草地左边界于点A,交OD的延长线于点B,再以D为圆心,DB长为半径画弧交草地的右边界于点C,
则扇形AOB和扇形BDC部分即为羊的活动区域.
23.
(1)证明:连接OD,
∵AD平分∠BAC,
∴∠OAD=∠CAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODB=90°,
∴OD⊥BC,
∴直线BC是⊙O的切线;
(2)解:由∠B=30°,∠C=90°,∠ODB=90°,
得:AB=2AC=12,OB=2OD,∠AOD=120°,
∠DAC=30°,
∵OA=OD,
∴OB=2OA,
∴OA=OD=4,
由∠DAC=30°,得DC=2,
∴S阴影=S扇形OAD-S△OAD
=
=π-4.
24.
解:(1)AC与⊙O的相切,理由如下,
,
,
,
,
又,
,
OD⊥BC,
,
,
,
是半径,
是的切线,
AC与⊙O的相切;
(2)过作于,如图,
设,
,
在中
,
,
,
解得,
,
,
,
,
,
在中,
,
,
扇形,
阴影部分扇形.
同课章节目录
