九年级数学上册试题 3.8.1 圆锥的侧面积-浙教版(含解析)
文档属性
| 名称 | 九年级数学上册试题 3.8.1 圆锥的侧面积-浙教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 673.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 07:24:29 | ||
图片预览


文档简介
3.8.1 圆锥的侧面积
一、单选题
1.已知圆锥的底面半径为,母线长为,则圆锥的侧面积为( )
A. B. C. D.
2.圆锥的截面是一个等边三角形,则它的侧面展开图圆心角度数是( )
A.60° B.90° C.120° D.180°
3.把一个弧长为10π cm的扇形AOC围成一个圆锥,测得母线OA=13 cm,则圆锥的高h为( )
A.12 cm B.10 cm C.6 cm D.5 cm
4.如图,一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是( )
A.1 B. C. D.
5.一个底面直径为2,高为3的圆锥的体积是( )
A. B.2 C.3 D.4
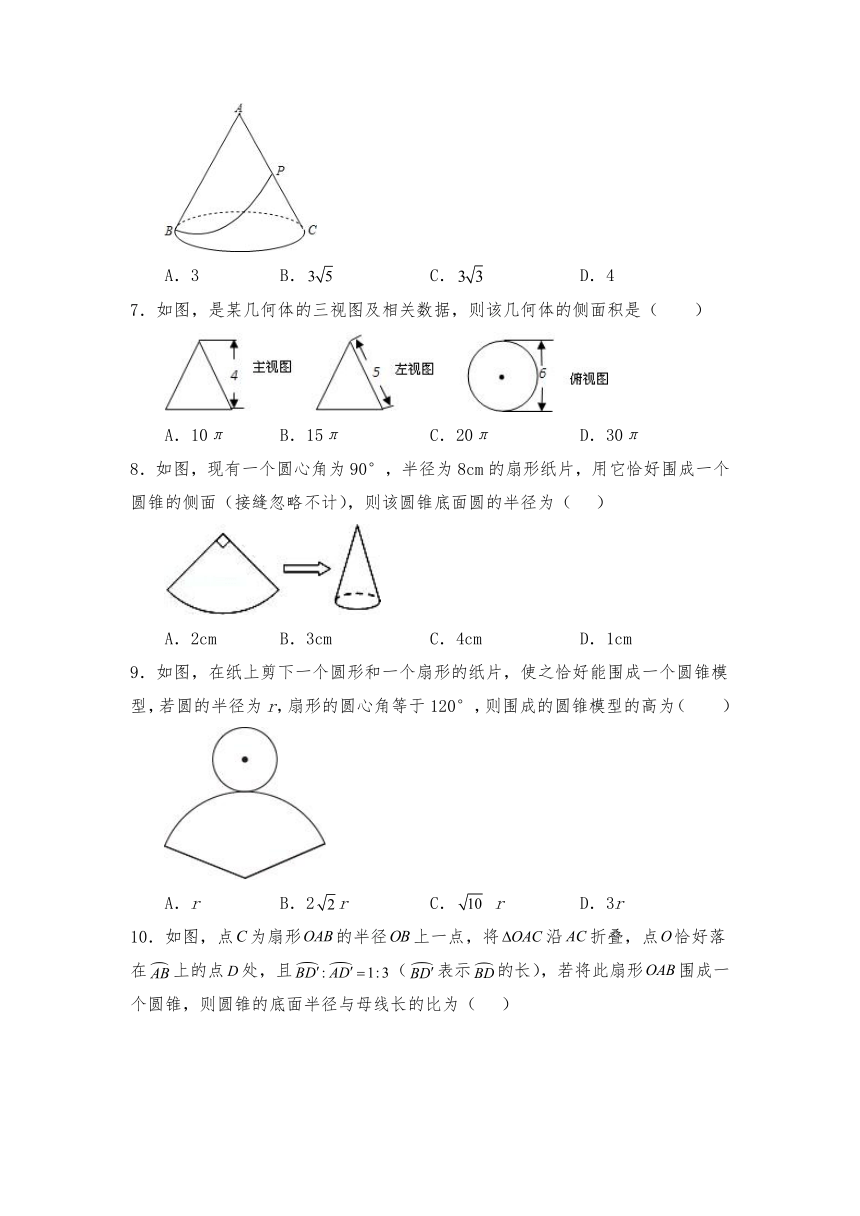
6.如图,有圆锥形粮堆,其正视图是边长为6的正三角形,粮堆母线的中点P处有一老鼠正在偷吃粮食,此时,小猫正在处,它要沿圆锥侧面到达P处,捕捉老鼠,则小猫所经过的最短路程是( )
A.3 B. C. D.4
7.如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( )
A.10π B.15π C.20π D.30π
8.如图,现有一个圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为( )
A.2cm B.3cm C.4cm D.1cm
9.如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )
A.r B.2r C. r D.3r
10.如图,点为扇形的半径上一点,将沿折叠,点恰好落在上的点处,且(表示的长),若将此扇形围成一个圆锥,则圆锥的底面半径与母线长的比为( )
A. B. C. D.
二、填空题
11.已知圆锥的母线长是9cm,它的侧面展开图的圆心角是120°,则圆锥的高为 _____cm.
12.若一个圆锥体的底面积是其表面积的,则其侧面展开图圆心角的度数为______________.
13.用一个半径为10cm半圆纸片围成一个圆锥的侧面(接缝忽略不计),则该圆锥的高为______.
14.如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,以边AC所在直线为轴将Rt△ABC旋转一周得到一个圆锥,则这个圆锥的侧面积是__________.
15.已知底面圆半径为1cm的圆锥的侧面积为3πcm2,则圆锥的母线长为_________cm.
16.如图,从一块直径是m的圆形铁皮上剪出一个圆心角为90°的扇形,将其围成一个圆锥,圆锥底面圆的半径是__________m.
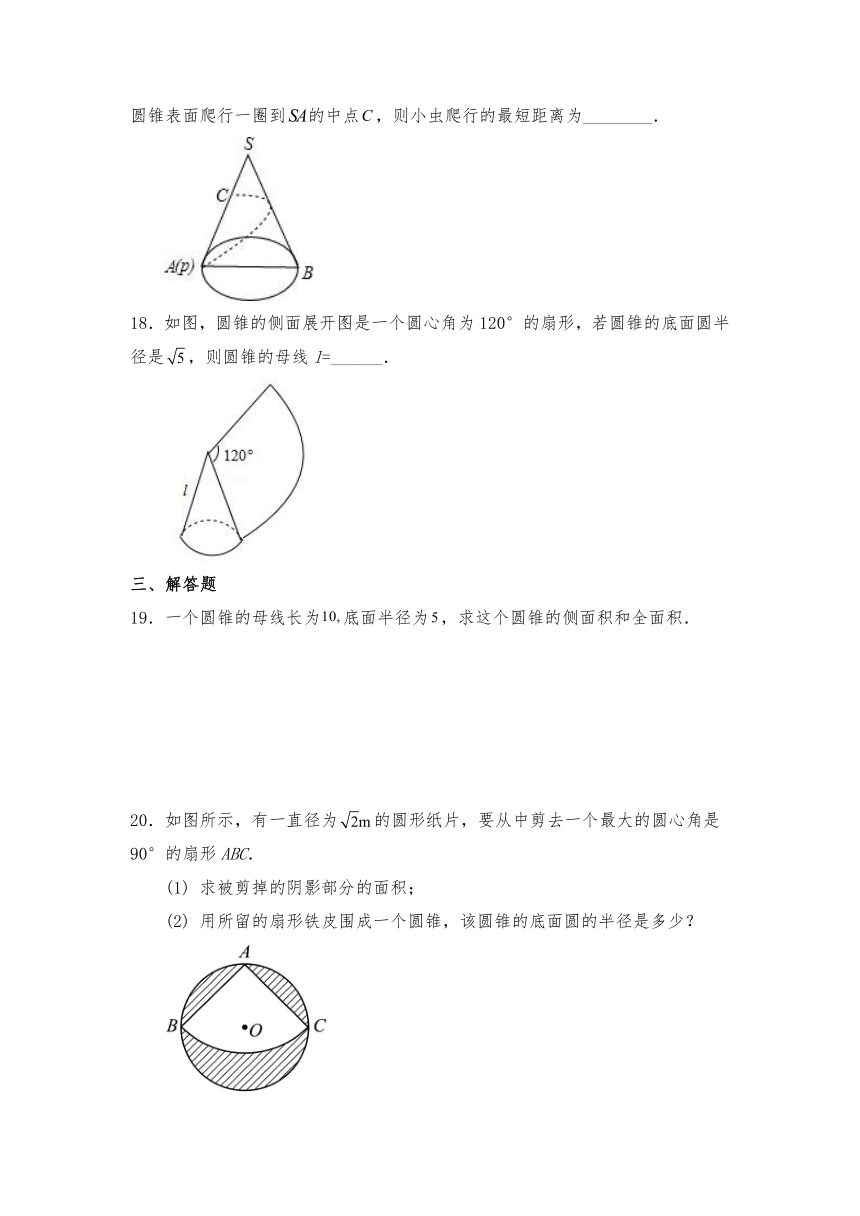
17.如图,圆锥的底面圆直径为,母线长为,若小虫从点开始绕着圆锥表面爬行一圈到的中点,则小虫爬行的最短距离为________.
18.如图,圆锥的侧面展开图是一个圆心角为120°的扇形,若圆锥的底面圆半径是,则圆锥的母线l=______.
三、解答题
19.一个圆锥的母线长为底面半径为,求这个圆锥的侧面积和全面积.
20.如图所示,有一直径为的圆形纸片,要从中剪去一个最大的圆心角是90°的扇形ABC.
(1) 求被剪掉的阴影部分的面积;
(2) 用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
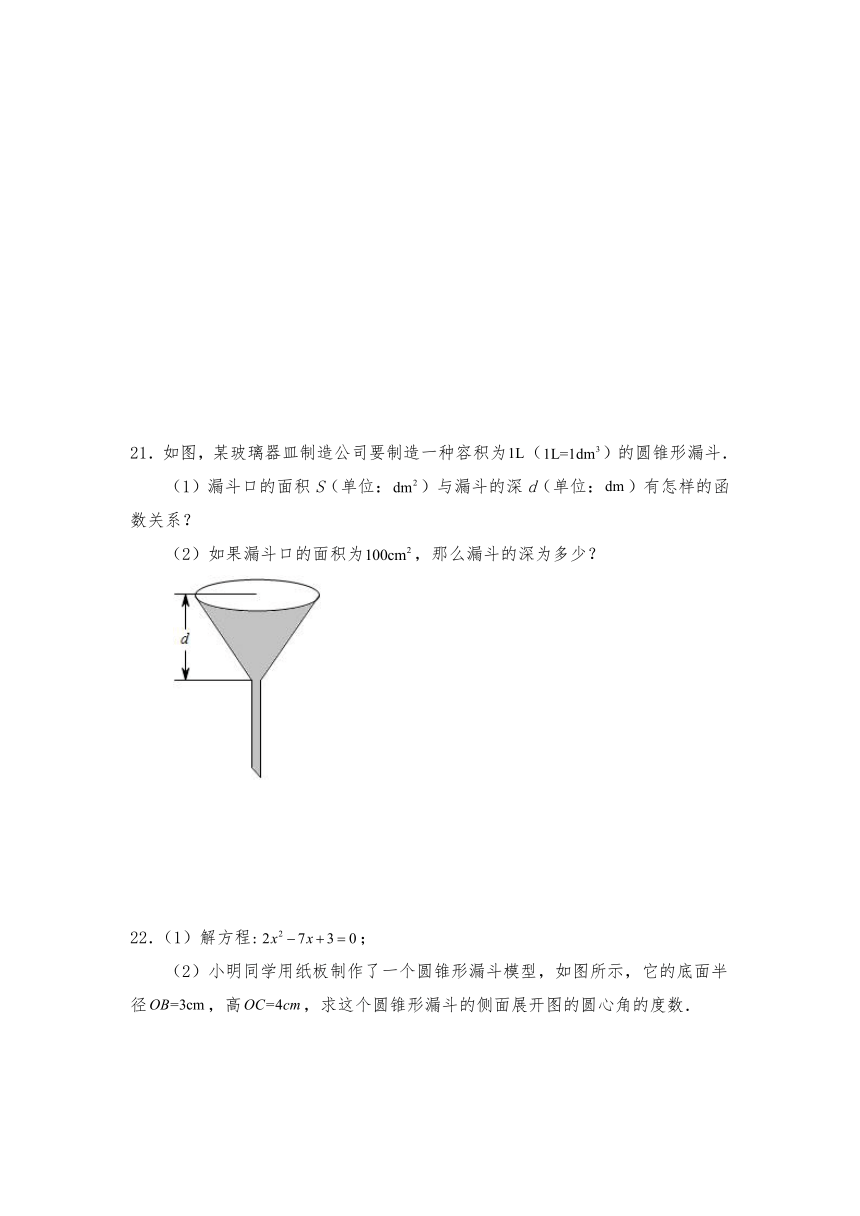
21.如图,某玻璃器皿制造公司要制造一种容积为()的圆锥形漏斗.
(1)漏斗口的面积S(单位:)与漏斗的深d(单位:)有怎样的函数关系?
(2)如果漏斗口的面积为,那么漏斗的深为多少?
22.(1)解方程:;
(2)小明同学用纸板制作了一个圆锥形漏斗模型,如图所示,它的底面半径,高,求这个圆锥形漏斗的侧面展开图的圆心角的度数.
23.如图,圆锥的轴截面是边长为的正三角形,P是母线的中点.求在圆锥的侧面上从B点到P点的最短路线的长.
24.如图,在一个半径为的圆形纸片中,剪一个圆心角为的扇形.
(1)求这个扇形的面积(保留);
(2)用所剪的纸片围成一个圆锥的侧面,求这个圆锥的底面圆的半径.
答案
一、单选题
1.B
【分析】利用圆锥侧面积计算公式计算即可:;
解: ,
故选B.
2.D
【分析】易得圆锥的底面直径与母线长相等,那么根据圆锥的底面周长等于侧面展开图的弧长即可得到这个圆锥的侧面展开图的圆心角度数.
解:设圆锥的底面半径为r,母线长为R,圆心角的度数为n度
∵它的轴截面是正三角形,∴R=2r,
∴2πr=,
解得n=180,
故展开图的圆心角为180°
故选:D.
3.A
【分析】利用弧长求出底面圆的半径,然后运用勾股定理求出圆锥的高.
解:设底面圆的半径为r,则:2πr=10π,得:r=5.
圆锥的高为:cm.
故选A.
4.C
【分析】根据侧面展开图的弧长等于圆锥的底面周长,即可求得底面周长,进而即可求得底面的半径长.
解:根据题意得:该圆锥的底面周长为,
∴该圆锥的底面半径是.
故选:C
5.A
【分析】圆锥的体积等于底面积乘以高的三分之一.
解:
故选A.
6.B
【分析】求这只小猫经过的最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离的问题.根据圆锥的轴截面是边长为的等边三角形可知,展开图是半径是6的半圆.点是半圆的一个端点,而点是平分半圆的半径的中点,根据勾股定理就可求出两点和在展开图中的距离,就是这只小猫经过的最短距离.
解:圆锥的底面周长是,则,
,即圆锥侧面展开图的圆心角是180度.
则在圆锥侧面展开图中,,度.
在圆锥侧面展开图中.
故小猫经过的最短距离是.故选:.
7.B
解:由三视图可知此几何体为圆锥,
∴圆锥的底面半径为3,母线长为5,
∵圆锥的底面周长等于圆锥的侧面展开扇形的弧长,
∴圆锥的底面周长=圆锥的侧面展开扇形的弧长=2πr=2π×3=6π,
∴圆锥的侧面积=lr=×6π×5=15π,
8.A
试题分析:本题的关键是利用弧长公式计算弧长,再利用底面周长=展开图的弧长可得.
解:L=,
解R=2cm.
故选 A.
9.B
解:∵圆的半径为r,扇形的弧长等于底面圆的周长得出2πr.
设圆锥的母线长为R,则=2πr,
解得:R=3r.
根据勾股定理得圆锥的高为2r.
故选:B.
10.D
【分析】连接OD,求出∠AOB,利用弧长公式和圆的周长公式求解即可.
解:连接交AC于.
由折叠的知识可得:,,
,
,
且,
设圆锥的底面半径为,母线长为,
,
.
故选D.
二、填空题
11.6
【分析】设圆锥底面半径为,那么圆锥底面圆周长为,所以侧面展开图的弧长为,然后利用扇形的面积公式即可得到关于的方程,解方程即可求得圆锥底面圆的半径,然后利用勾股定理求得圆锥的高即可.
解:设圆锥底面半径为,
那么圆锥底面圆周长为,
所以侧面展开图的弧长为,
,
解得:,
圆锥的高为,
故答案为:.
12.120°
【分析】根据圆锥的底面积是其表面积的,则得到圆锥底面半径和母线长的关系,根据圆锥侧面展开图的弧长=底面周长即可求得圆锥侧面展开图的圆心角度数.
解:设底面圆的半径为,侧面展开扇形的半径为R,扇形的圆心角为n°.
由题意得,
,
∵个圆锥体的底面积是其表面积的,
∴,
.
由得,
故.
由得:
,
解得.
故答案为:120°.
13.
【分析】根据半圆的弧长等于圆锥的底圆周长可以求出圆锥底圆的半径,又由半圆的半径等于圆锥的母线,然后利用勾股定理求出圆锥的高.
解:如图所示:
圆锥的侧面展开图的弧长为(cm),
∴圆锥的底面半径为(cm),
∴圆锥的高为:(cm).
故答案是:cm.
14.65π
【分析】先得到所得圆锥的母线和底面半径,再利用扇形面积计算.
解:由已知得,母线长AB=13,半径r为5,
∴圆锥的侧面积==65π,
故答案为:65π.
15.3
【分析】根据圆的周长公式求出圆锥的底面周长,根据圆锥的侧面积的计算公式计算即可.
设圆锥的母线长为Rcm,
解:圆锥的底面周长=2π×1=2π,设母线长为R,
则×2π×R=3π,
解得,R=3(cm),
故答案为3.
16.
【分析】首先求得扇形的弧长,然后利用圆的周长公式即可求解.
解:连接BC、AO,
∵⊙O的直径为m,
∴半径是m,
∵AB=AC,OB=OC,
∴BC⊥AO,AO=BO=m,
在Rt△ABO中,AB=m,
∴圆锥底面圆的弧长,
设圆锥底面圆的半径是r,
则,
∴m,
故答案为:.
17.
【分析】将圆锥的侧面展开,是一个扇形,AC就是小虫爬行的最短路程,利用弧长与圆心角的公式,求展开图的圆心角,R=4,l=2πr=2π,可求出n的大小,由于n=90 ,利用勾股定理可求AC的长即可.
解:把圆锥的侧面展开,弧长是2πr=2π,母线AS=4,
侧面展开的圆心角,n=90 即∠ASC=90 ,
C为AD的中点SD=2,
线段AC是小虫爬行的最短距离,
在Rt△SAC中,由勾股定理的AC=,
故答案为:.
18..
解:扇形的弧长和圆锥的底面周长相等,即:,解得:l=
三、解答题
19.
解:这个圆锥的侧面积
这个圆锥的全面积=50π+π×52=75π.
20.
(1)解:如图,连结BC,
∵∠A=90°,
∴BC为⊙O的直径.即,
在Rt△ABC中,AB=AC,且AB2+AC2=BC2,
∴AB=AC=1,
∴=;
(2)解:设圆锥底面半径为r,则的长为2πr,
∴,
∴.
21.
解:(1)根据圆锥体积=×底面积×高,得,
则,
故漏斗口的面积S与漏斗的深度d之间的函数关系为:;
(2)∵S=100cm2=1dm2,
∴,
解得d=3dm=30cm,
故漏斗口的面积为100cm2,那么漏斗的深为30cm.
22.
解:(1)
a=2,b=-7,c=3
∴x=
解得:;
(2)该圆锥侧面展开图的半径BC=
侧面展开图的弧长即为底面圆的周长为cm
∴侧面展开图的圆心角的度数为
答:这个圆锥形漏斗的侧面展开图的圆心角的度数为216°.
23.
解:圆锥底面是以BC为直径的圆,圆的周长是6π,将圆锥展开,就得到一个以A为圆心,以AB为半径的扇形,弧长是l=6π,
设展开后的圆心角是n°,则,
解得:n=180°,
则∠BAC=×180°=90°,
AP=AC=3,AB=6,
则在圆锥的侧面上从B点到P点的最短路线的长就是展开后线段BP的长,
如图,
由勾股定理得:BP=,
答:在圆锥的侧面上从B点到P点的最短路线的长是3cm.
24.
解:(1)如图,连接,∵,
∴为的直径,
∵为扇形,∵,
∴为等腰直角三角形,
∴
∴,
∴这个扇形的面积;
(2)设这个圆锥的底面圆的半径为,由题意得的长即为底面圆的周长
∵扇形中,的长,
∴,解得,即围成的这个圆锥的底面圆的半径为1.
一、单选题
1.已知圆锥的底面半径为,母线长为,则圆锥的侧面积为( )
A. B. C. D.
2.圆锥的截面是一个等边三角形,则它的侧面展开图圆心角度数是( )
A.60° B.90° C.120° D.180°
3.把一个弧长为10π cm的扇形AOC围成一个圆锥,测得母线OA=13 cm,则圆锥的高h为( )
A.12 cm B.10 cm C.6 cm D.5 cm
4.如图,一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是( )
A.1 B. C. D.
5.一个底面直径为2,高为3的圆锥的体积是( )
A. B.2 C.3 D.4
6.如图,有圆锥形粮堆,其正视图是边长为6的正三角形,粮堆母线的中点P处有一老鼠正在偷吃粮食,此时,小猫正在处,它要沿圆锥侧面到达P处,捕捉老鼠,则小猫所经过的最短路程是( )
A.3 B. C. D.4
7.如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( )
A.10π B.15π C.20π D.30π
8.如图,现有一个圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为( )
A.2cm B.3cm C.4cm D.1cm
9.如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )
A.r B.2r C. r D.3r
10.如图,点为扇形的半径上一点,将沿折叠,点恰好落在上的点处,且(表示的长),若将此扇形围成一个圆锥,则圆锥的底面半径与母线长的比为( )
A. B. C. D.
二、填空题
11.已知圆锥的母线长是9cm,它的侧面展开图的圆心角是120°,则圆锥的高为 _____cm.
12.若一个圆锥体的底面积是其表面积的,则其侧面展开图圆心角的度数为______________.
13.用一个半径为10cm半圆纸片围成一个圆锥的侧面(接缝忽略不计),则该圆锥的高为______.
14.如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,以边AC所在直线为轴将Rt△ABC旋转一周得到一个圆锥,则这个圆锥的侧面积是__________.
15.已知底面圆半径为1cm的圆锥的侧面积为3πcm2,则圆锥的母线长为_________cm.
16.如图,从一块直径是m的圆形铁皮上剪出一个圆心角为90°的扇形,将其围成一个圆锥,圆锥底面圆的半径是__________m.
17.如图,圆锥的底面圆直径为,母线长为,若小虫从点开始绕着圆锥表面爬行一圈到的中点,则小虫爬行的最短距离为________.
18.如图,圆锥的侧面展开图是一个圆心角为120°的扇形,若圆锥的底面圆半径是,则圆锥的母线l=______.
三、解答题
19.一个圆锥的母线长为底面半径为,求这个圆锥的侧面积和全面积.
20.如图所示,有一直径为的圆形纸片,要从中剪去一个最大的圆心角是90°的扇形ABC.
(1) 求被剪掉的阴影部分的面积;
(2) 用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
21.如图,某玻璃器皿制造公司要制造一种容积为()的圆锥形漏斗.
(1)漏斗口的面积S(单位:)与漏斗的深d(单位:)有怎样的函数关系?
(2)如果漏斗口的面积为,那么漏斗的深为多少?
22.(1)解方程:;
(2)小明同学用纸板制作了一个圆锥形漏斗模型,如图所示,它的底面半径,高,求这个圆锥形漏斗的侧面展开图的圆心角的度数.
23.如图,圆锥的轴截面是边长为的正三角形,P是母线的中点.求在圆锥的侧面上从B点到P点的最短路线的长.
24.如图,在一个半径为的圆形纸片中,剪一个圆心角为的扇形.
(1)求这个扇形的面积(保留);
(2)用所剪的纸片围成一个圆锥的侧面,求这个圆锥的底面圆的半径.
答案
一、单选题
1.B
【分析】利用圆锥侧面积计算公式计算即可:;
解: ,
故选B.
2.D
【分析】易得圆锥的底面直径与母线长相等,那么根据圆锥的底面周长等于侧面展开图的弧长即可得到这个圆锥的侧面展开图的圆心角度数.
解:设圆锥的底面半径为r,母线长为R,圆心角的度数为n度
∵它的轴截面是正三角形,∴R=2r,
∴2πr=,
解得n=180,
故展开图的圆心角为180°
故选:D.
3.A
【分析】利用弧长求出底面圆的半径,然后运用勾股定理求出圆锥的高.
解:设底面圆的半径为r,则:2πr=10π,得:r=5.
圆锥的高为:cm.
故选A.
4.C
【分析】根据侧面展开图的弧长等于圆锥的底面周长,即可求得底面周长,进而即可求得底面的半径长.
解:根据题意得:该圆锥的底面周长为,
∴该圆锥的底面半径是.
故选:C
5.A
【分析】圆锥的体积等于底面积乘以高的三分之一.
解:
故选A.
6.B
【分析】求这只小猫经过的最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离的问题.根据圆锥的轴截面是边长为的等边三角形可知,展开图是半径是6的半圆.点是半圆的一个端点,而点是平分半圆的半径的中点,根据勾股定理就可求出两点和在展开图中的距离,就是这只小猫经过的最短距离.
解:圆锥的底面周长是,则,
,即圆锥侧面展开图的圆心角是180度.
则在圆锥侧面展开图中,,度.
在圆锥侧面展开图中.
故小猫经过的最短距离是.故选:.
7.B
解:由三视图可知此几何体为圆锥,
∴圆锥的底面半径为3,母线长为5,
∵圆锥的底面周长等于圆锥的侧面展开扇形的弧长,
∴圆锥的底面周长=圆锥的侧面展开扇形的弧长=2πr=2π×3=6π,
∴圆锥的侧面积=lr=×6π×5=15π,
8.A
试题分析:本题的关键是利用弧长公式计算弧长,再利用底面周长=展开图的弧长可得.
解:L=,
解R=2cm.
故选 A.
9.B
解:∵圆的半径为r,扇形的弧长等于底面圆的周长得出2πr.
设圆锥的母线长为R,则=2πr,
解得:R=3r.
根据勾股定理得圆锥的高为2r.
故选:B.
10.D
【分析】连接OD,求出∠AOB,利用弧长公式和圆的周长公式求解即可.
解:连接交AC于.
由折叠的知识可得:,,
,
,
且,
设圆锥的底面半径为,母线长为,
,
.
故选D.
二、填空题
11.6
【分析】设圆锥底面半径为,那么圆锥底面圆周长为,所以侧面展开图的弧长为,然后利用扇形的面积公式即可得到关于的方程,解方程即可求得圆锥底面圆的半径,然后利用勾股定理求得圆锥的高即可.
解:设圆锥底面半径为,
那么圆锥底面圆周长为,
所以侧面展开图的弧长为,
,
解得:,
圆锥的高为,
故答案为:.
12.120°
【分析】根据圆锥的底面积是其表面积的,则得到圆锥底面半径和母线长的关系,根据圆锥侧面展开图的弧长=底面周长即可求得圆锥侧面展开图的圆心角度数.
解:设底面圆的半径为,侧面展开扇形的半径为R,扇形的圆心角为n°.
由题意得,
,
∵个圆锥体的底面积是其表面积的,
∴,
.
由得,
故.
由得:
,
解得.
故答案为:120°.
13.
【分析】根据半圆的弧长等于圆锥的底圆周长可以求出圆锥底圆的半径,又由半圆的半径等于圆锥的母线,然后利用勾股定理求出圆锥的高.
解:如图所示:
圆锥的侧面展开图的弧长为(cm),
∴圆锥的底面半径为(cm),
∴圆锥的高为:(cm).
故答案是:cm.
14.65π
【分析】先得到所得圆锥的母线和底面半径,再利用扇形面积计算.
解:由已知得,母线长AB=13,半径r为5,
∴圆锥的侧面积==65π,
故答案为:65π.
15.3
【分析】根据圆的周长公式求出圆锥的底面周长,根据圆锥的侧面积的计算公式计算即可.
设圆锥的母线长为Rcm,
解:圆锥的底面周长=2π×1=2π,设母线长为R,
则×2π×R=3π,
解得,R=3(cm),
故答案为3.
16.
【分析】首先求得扇形的弧长,然后利用圆的周长公式即可求解.
解:连接BC、AO,
∵⊙O的直径为m,
∴半径是m,
∵AB=AC,OB=OC,
∴BC⊥AO,AO=BO=m,
在Rt△ABO中,AB=m,
∴圆锥底面圆的弧长,
设圆锥底面圆的半径是r,
则,
∴m,
故答案为:.
17.
【分析】将圆锥的侧面展开,是一个扇形,AC就是小虫爬行的最短路程,利用弧长与圆心角的公式,求展开图的圆心角,R=4,l=2πr=2π,可求出n的大小,由于n=90 ,利用勾股定理可求AC的长即可.
解:把圆锥的侧面展开,弧长是2πr=2π,母线AS=4,
侧面展开的圆心角,n=90 即∠ASC=90 ,
C为AD的中点SD=2,
线段AC是小虫爬行的最短距离,
在Rt△SAC中,由勾股定理的AC=,
故答案为:.
18..
解:扇形的弧长和圆锥的底面周长相等,即:,解得:l=
三、解答题
19.
解:这个圆锥的侧面积
这个圆锥的全面积=50π+π×52=75π.
20.
(1)解:如图,连结BC,
∵∠A=90°,
∴BC为⊙O的直径.即,
在Rt△ABC中,AB=AC,且AB2+AC2=BC2,
∴AB=AC=1,
∴=;
(2)解:设圆锥底面半径为r,则的长为2πr,
∴,
∴.
21.
解:(1)根据圆锥体积=×底面积×高,得,
则,
故漏斗口的面积S与漏斗的深度d之间的函数关系为:;
(2)∵S=100cm2=1dm2,
∴,
解得d=3dm=30cm,
故漏斗口的面积为100cm2,那么漏斗的深为30cm.
22.
解:(1)
a=2,b=-7,c=3
∴x=
解得:;
(2)该圆锥侧面展开图的半径BC=
侧面展开图的弧长即为底面圆的周长为cm
∴侧面展开图的圆心角的度数为
答:这个圆锥形漏斗的侧面展开图的圆心角的度数为216°.
23.
解:圆锥底面是以BC为直径的圆,圆的周长是6π,将圆锥展开,就得到一个以A为圆心,以AB为半径的扇形,弧长是l=6π,
设展开后的圆心角是n°,则,
解得:n=180°,
则∠BAC=×180°=90°,
AP=AC=3,AB=6,
则在圆锥的侧面上从B点到P点的最短路线的长就是展开后线段BP的长,
如图,
由勾股定理得:BP=,
答:在圆锥的侧面上从B点到P点的最短路线的长是3cm.
24.
解:(1)如图,连接,∵,
∴为的直径,
∵为扇形,∵,
∴为等腰直角三角形,
∴
∴,
∴这个扇形的面积;
(2)设这个圆锥的底面圆的半径为,由题意得的长即为底面圆的周长
∵扇形中,的长,
∴,解得,即围成的这个圆锥的底面圆的半径为1.
同课章节目录
