九年级数学上册试题 3.8弧长及扇形的面积同步练习-浙教版(含解析)
文档属性
| 名称 | 九年级数学上册试题 3.8弧长及扇形的面积同步练习-浙教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 00:00:00 | ||
图片预览

文档简介
3.8弧长及扇形的面积
一、单选题
1.如图,将⊙O沿弦AB折叠,恰好经过圆心O,若⊙O的半径为3,则的长为( )
A. B. C. D.
2.一个扇形的弧长是,其圆心角是150°,此扇形的面积为( )
A. B. C. D.
3.一个扇形的弧长是12πcm,面积是108πcm2,则此扇形的圆心角的度数是( )
A.300° B.150° C.120° D.75°
4.如图,扇形OBA中,点C在弧AB上,连接BC,P为BC中点.若,,则点C沿弧从点B运动到点A的过程中,点P所经过的路径长为( )
A. B. C. D.6
5.如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接.若,则图中阴影部分的面积是( )
A. B. C. D.
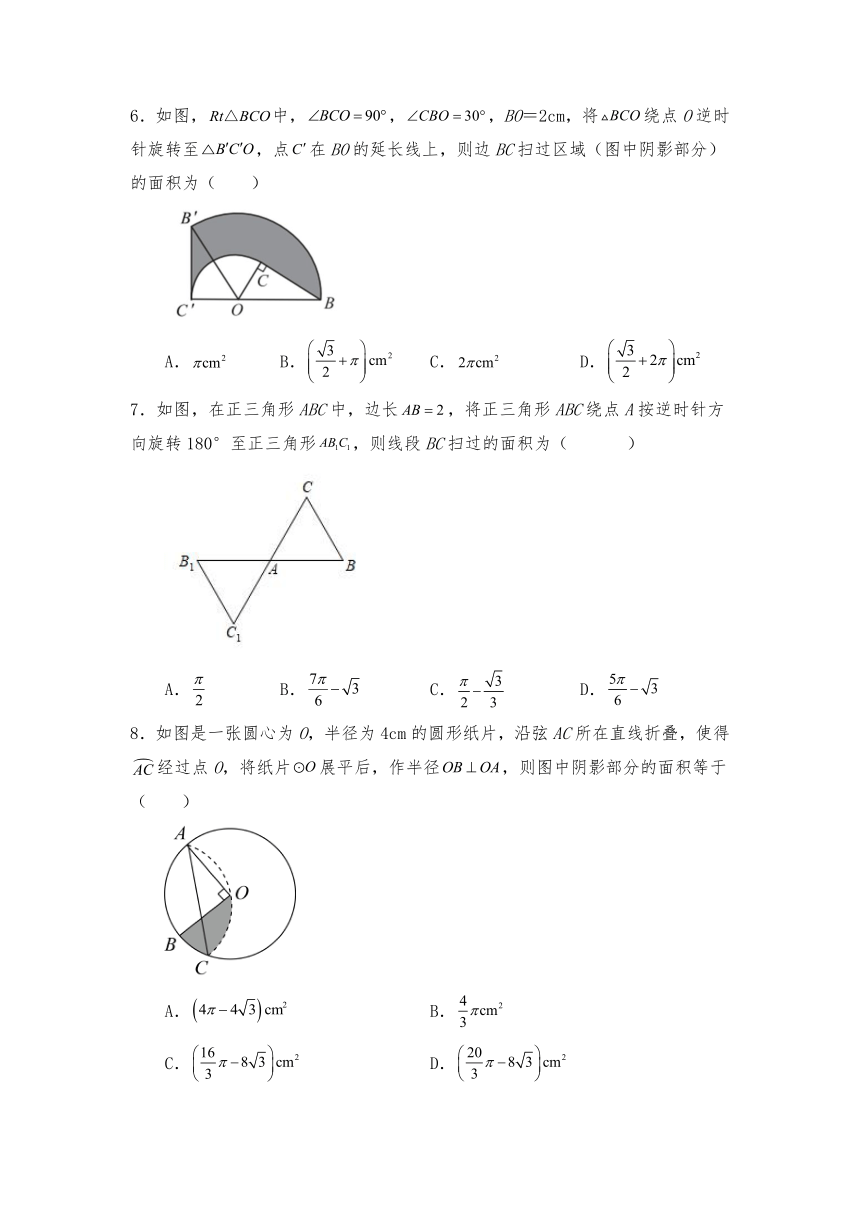
6.如图,中,,,BO=2cm,将绕点O逆时针旋转至,点在BO的延长线上,则边BC扫过区域(图中阴影部分)的面积为( )
A. B. C. D.
7.如图,在正三角形ABC中,边长,将正三角形ABC绕点A按逆时针方向旋转180°至正三角形,则线段BC扫过的面积为( )
A. B. C. D.
8.如图是一张圆心为O,半径为4cm的圆形纸片,沿弦AC所在直线折叠,使得经过点O,将纸片展平后,作半径,则图中阴影部分的面积等于( )
A. B.
C. D.
9.如图,在矩形ABCD中,AC为对角线,,,以B为圆心,AB长为半径画弧,交AC于点M,交BC于点N,则阴影部分的面积为( )
A. B. C. D.
10.如图,两个半径长均为的直角扇形的圆心分别在对方的圆弧上,扇形的圆心C是的中点,且扇形绕着点C旋转,半径,交于点G,半径,交于点H,则图中阴影面积等于( )
A. B. C. D.
二、填空题
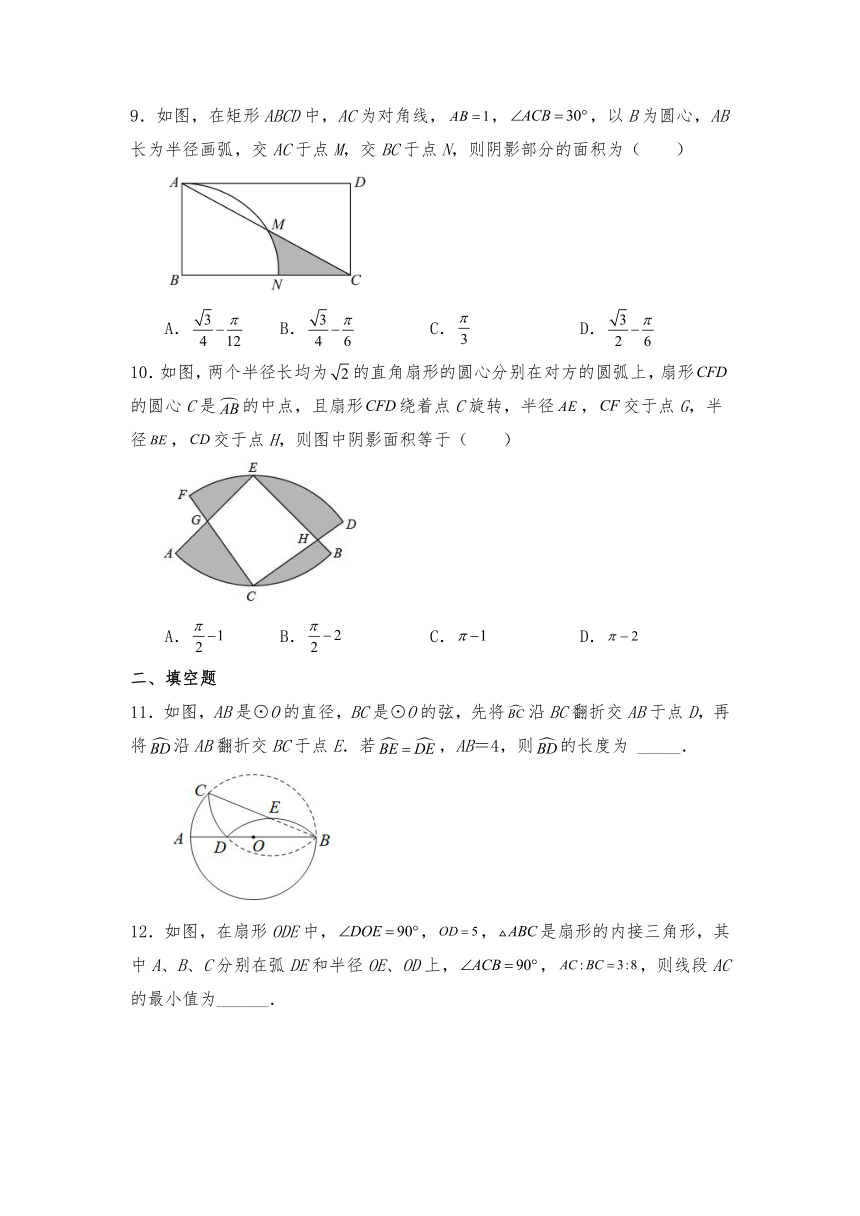
11.如图,AB是⊙O的直径,BC是⊙O的弦,先将沿BC翻折交AB于点D,再将沿AB翻折交BC于点E.若,AB=4,则的长度为 _____.
12.如图,在扇形ODE中,,,是扇形的内接三角形,其中A、B、C分别在弧DE和半径OE、OD上,,,则线段AC的最小值为______.
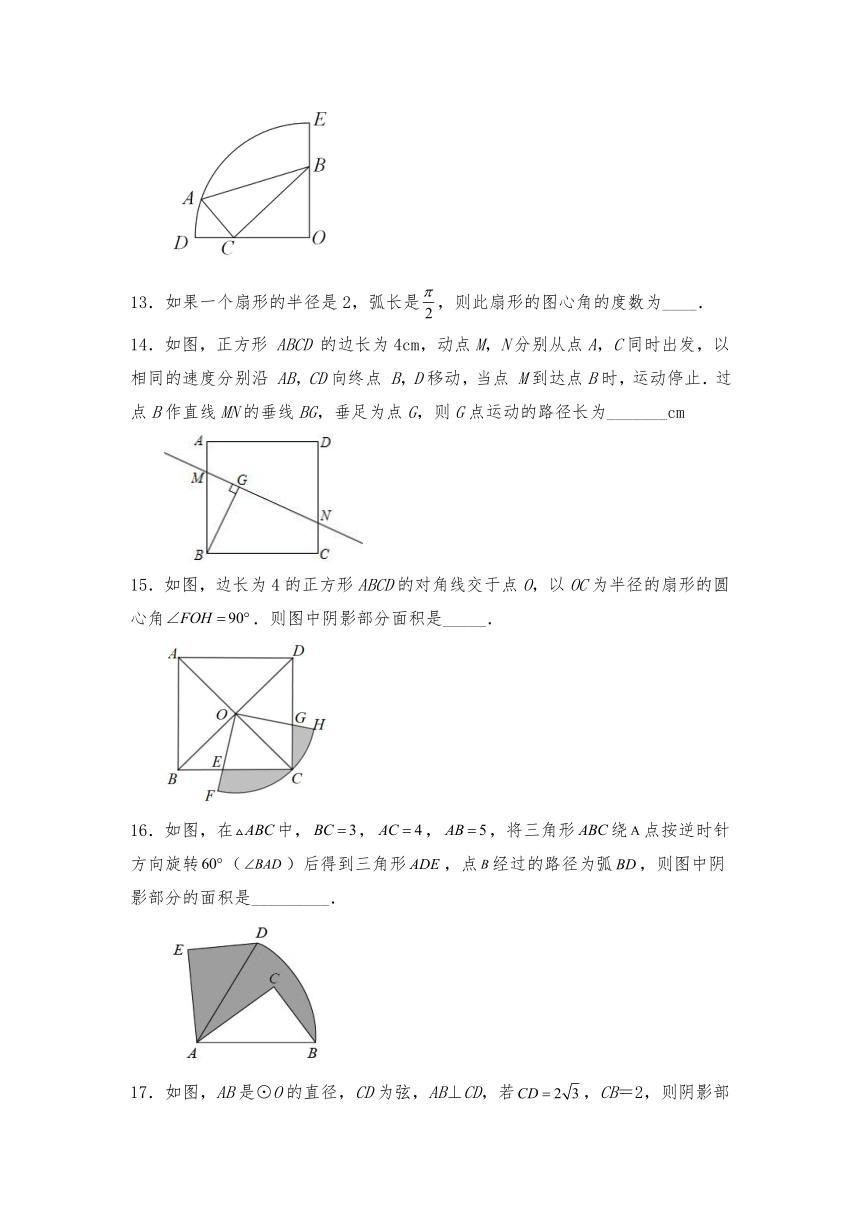
13.如果一个扇形的半径是2,弧长是,则此扇形的图心角的度数为____.
14.如图,正方形 ABCD 的边长为4cm,动点M,N分别从点A,C同时出发,以相同的速度分别沿 AB,CD向终点 B,D移动,当点 M到达点B时,运动停止.过点B作直线MN的垂线BG,垂足为点G,则G点运动的路径长为_______cm
15.如图,边长为4的正方形ABCD的对角线交于点O,以OC为半径的扇形的圆心角.则图中阴影部分面积是_____.
16.如图,在中,,,,将三角形绕点按逆时针方向旋转()后得到三角形,点经过的路径为弧,则图中阴影部分的面积是_________.
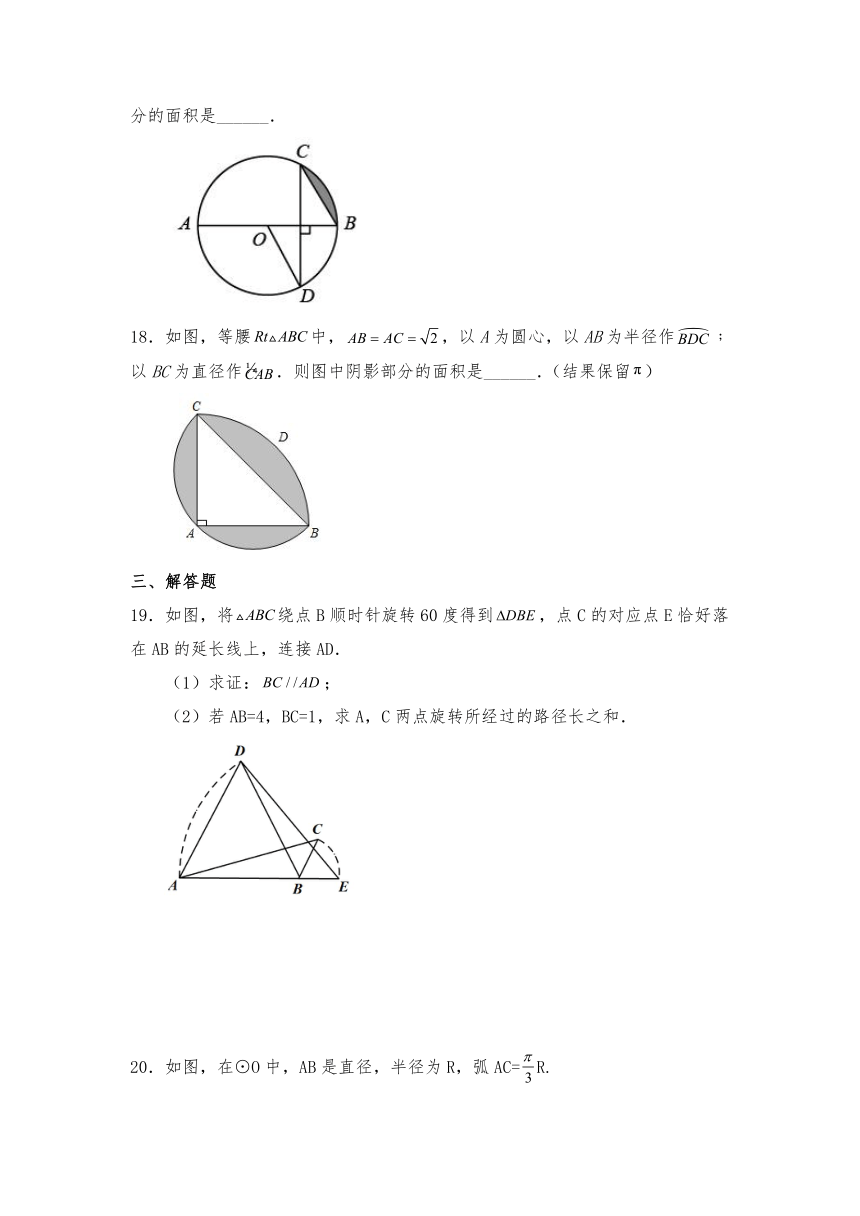
17.如图,AB是⊙O的直径,CD为弦,AB⊥CD,若,CB=2,则阴影部分的面积是______.
18.如图,等腰中,,以A为圆心,以AB为半径作﹔以BC为直径作.则图中阴影部分的面积是______.(结果保留)
三、解答题
19.如图,将绕点B顺时针旋转60度得到,点C的对应点E恰好落在AB的延长线上,连接AD.
(1)求证:;
(2)若AB=4,BC=1,求A,C两点旋转所经过的路径长之和.
20.如图,在⊙O中,AB是直径,半径为R,弧AC=R.
求:(1)∠AOC的度数.(2)若D为劣弧BC上的一动点,且弦AD与半径OC交于E点.试探求△AEC≌△DEO时,D点的位置.
21.如图,边长为的等边△ABC内接于⊙O,D为劣弧上一点,过点B作BE⊥OD于点E,当点D从点B沿劣弧运动到点C时,求点E经过的路径长.
22.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
23.如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°
(1)画出旋转之后的△AB′C′;
(2)求线段AC旋转过程中扫过的扇形的面积.
24.如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1)求证:OF∥BC;
(2)求证:△AFO≌△CEB;
(3)若EB=5cm,CD=cm,设OE=x,求x值及阴影部分的面积.
答案
一、单选题
1.C
【分析】连接OA、OB,作OC⊥AB于C,根据翻转变换的性质得到OC=OA,根据等腰三角形的性质、三角形内角和定理求出∠AOB,根据弧长公式计算即可.
解:连接OA、OB,作OC⊥AB于C,
由题意得,OC=OA,
∴∠OAC=30°,
∵OA=OB,
∴∠OBA=∠OAC=30°,
∴∠AOB=120°,
∴劣的长==2π,
故选:C.
2.B
【分析】先求出该扇形的半径,再求其面积即可;
解:该扇形的半径为:,
∴扇形的面积为:,
故选:B.
3.C
【分析】先根据扇形面积公式求出半径,再根据弧长公式解答即可.
解:设扇形所在的圆的半径为rcm,圆心角为n°,由题意得:,解得:r=18,
∵,
∴此扇形的圆心角n=120°.
故选:C.
4.B
【分析】连接OC、OP,易得∠OPB=90°,点P是在以OB的中点D为圆心,BD为半径的圆上运动,求即可.
解:连接OC、OP,
∵OB=OC,
∴△BOC为等腰三角形,
∵P为BC中点,
∴OP⊥BC(三线合一),
即∠OPB=90°,
∴点P是在以OB的中点D为圆心,BD为半径的圆上运动,如图所示,
当点C运动到点A时,点P到达位置,
点P所经过的路径长为,
连接,∵D为OB中点,为AB中点,
∴∥OA,
∴=,BD=OA=3,
∴,
即点P所经过的路径长为 ,
故选:B.
5.B
【分析】连接CO,且直线l与AO交于点D,解直角三角形求出,即可求出扇形的面积,再算出的面积,即可求出阴影部分面积.
解:连接CO,且直线l与AO交于点D,如图所示,
∵扇形中,,
∴,
∵点A与圆心O重合,
∴,,
∴,
∴,
由勾股定理得:,
∵,,
∴,
故选:B.
6.A
【分析】先在Rt△OCB中利用特殊角求出OC、BC、∠COB,进而可求出,接着可以求出,则可以表示出、、,则阴影部分的面积可求.
解:在Rt△OCB中,∠CBO=30°,BO=1,
∴∠COB=60°,2OC=BO=BC,
∴,BC=,OC=1,
∴,
∴,
根据旋转的性质可知,,,,
∴,,,
∴,
∴(cm2),
故选:A.
7.B
【分析】分别取BC,的中点为D,,把所求面积分解成三部分在进行求解即可;
解:如图,BC扫过的面积即为阴影部分的面积;
分别取BC,的中点为D,,
∴,
∵等于大半圆面积减去小半圆面积,,
∴,
∵是所对弓形的面积的一半,
∴,
∴,
∴;
故选B.
8.A
【分析】作OD⊥AC交圆于点D、交AC于点E,根据垂径定理,OD平分 和,又因为AC是对折线,所以OD与AC互相垂直平分,所以ODCO组成的图形面积是与组成的图形面积的一半,也就等于ADCEA组成图形面积,此部分面积可用扇形OAC的面积减去△OAC面积求出,再用求出的面积减去扇形ODB的面积即得阴影部分面积.
解:作OD⊥AC交圆于点D,交AC于点E,连接OC,如图,
∴OD垂直平分弦AC,平分 和,
∵AC是向圆内的折线,且弦AC折叠后经过点O,
∴点O是点D关于AC的对称点,即OD与AC互相垂直平分,
∴OE=DE=OD
设与弦AC构成的图形面积为SADC,与构成的图形面积为SADCO,与和线段OD构成的图形面积为SODC,
则SADC=SADCO,SODC=SADCO,
∴SODC=SADC,
∵OD、OA都是圆O的半径,半径为4cm,
∴OE=OD=OA=,
∴∠OAE=30°,
∴∠AOE=90°-30°=60°,
∴∠AOC=2∠AOE=2×60°=120°,
∴S扇形OAC==(cm2),
∵AC=2AE=cm,
∴S△OAC=(cm2),
∴SADC= S扇形OAC - S△OAC=()(cm2),
∴SODC=()(cm2),
∵OB⊥OA,∠AOE=60°,
∴∠BOD=∠AOB-∠AOE=90°-60°=30°,
∴S扇形OBD=(cm2),
∴S阴影=SODC- S扇形OBD==()(cm2),
故选 A.
9.A
【分析】连接BM,过M作MH⊥BC于H,由∠ACB=30°得到∠BAC=60°,求得△ABM是等边三角形,得到∠ABM=60°,推出∠MBN=30°,根据三角形和扇形的面积公式即可得到结论.
解:连接BM,过M作MH⊥BC于H,
在矩形ABCD中,∠ABC=90°,
∵AB=1,∠ACB=30°,
∴∠BAC=60°,AC=2AB=2,BC=,
∵BA=BM,
∴△ABM是等边三角形,
∴∠ABM=60°,
∴∠MBN=30°,
∴MH=BM=,
∴S阴=S△BCM-S扇形BMN==,
故选:A.
10.D
【分析】先根据扇形面积公式求出两扇形面积,再过C分别作CM⊥AE于M,CN⊥BE于N,连接EC,再证明△CMG≌△CNH,可证得白色部分的面积等于对角线为的正方形CMEN得面积,进而可求得阴影部分的面积.
解:∵两个直角扇形的半径长均为,
∴两个扇形面积和为,
过C分别作CM⊥AE于M,CN⊥BE于N,连接EC,则四边形CMEN是矩形,
∵C是的中点,
∴∠AEC=∠BEC,即EC平分∠AEB,
∴CM=CN,
∴四边形CMEN是正方形,
∴∠CMG=∠MCN=∠CNH,
∴∠MCG+∠GCN=∠NCH+∠GCN=90°,
∴∠MCG=∠NCH,
∴△CMG≌△CNH(ASA),
∴白色部分的面积等于对角线为的正方形CMEN的面积,
∴空白部分面积为,
∴阴影部分面积为,
故选:D.
二、填空题
11.
【分析】由同圆或等圆中相等的圆周角所对的弧相等可得,因此.结合AB是的直径,可得所对的圆心角的度数.再利用弧长公式计算的长即可.
解:∵、、、所在的圆是等圆
又∵、、所对的圆周角都是
∴==
又∵=
∴===
又∵ +++=
∴=
∴
又∵AB是的直径
∴所对的圆心角为
∴的长=
故答案为
12.
【分析】取BC的中点M,连接AM,OM,AO.AM+OM≥OA,当且仅当A、M、O三点共线时等号成立,这样问题迎刃而解.
解:取BC的中点M,连接AM,OM,AO.
∵AC:BC=3:8,
∴可以假设AC=3k,BC=8k,则CM=BM=4k,
∵∠ACB=∠COB=90°,
∴
∵AM+OM≥OA,
∴5k+4k≥5,
∴k≥,
∴k的最小值为,
∴AC的最小值为,
故答案为.
13.45°
【分析】直接利用扇形弧长公式代入求出即可.
解:∵扇形的弧长是,半径为2,
∴,
解得:n=45,
故答案为:45°.
14.
【分析】连接BD,AC相交于O,在运动过程中,,得到点G的轨迹为以OB 为直径的半圆,G点轨迹长度等于半圆弧长,即可算出.
解:连接BD,AC相交于O
在运动过程中,
故点G的轨迹为以OB为直径的半圆
G点轨迹长度等于半圆弧长,
即:
故答案为:.
15.
【分析】证明△OCG≌△OBE,经过观察易得出结论:阴影部分面积=扇形面积-正方形面积的.
解:∵四边形ABCD为正方形,
∴OB=OC,∠BOC=90°,∠OBE=∠OCG=45°,
∵扇形的圆心角,
∴∠BOC-∠COE=∠FOH-∠COE,即∠BOE=∠COG,
在△OCG和△OBE中,
∠OBE=∠OCG,∠BOE=∠COG, OB=OC
∴△OCG≌△OBE,
∵正方形边长为4,
∴AC=,
∴OC=
∵,
=
=
=
故答案为:
16.
【分析】把△ADE顺时针方向旋转60°到△ABC,要求的阴影部分的面积就是边长为5,角为60°的扇形面积.
解:圆形面积= =25π
扇形的面积= =
17.
【分析】连接OC,设CD与AB的交点为E,利用垂径定理、勾股定理判定△OBC是等边三角形,运用扇形的面积减去△OBC的面积即可.
解:连接OC,设CD与AB的交点为E,
∵AB是⊙O的直径,AB⊥CD,,CB=2,
∴,,
∴∠ECB=30°,∠CBE=60°,
∵CO=BO,
∴△OBC是等边三角形,
∴∠BOC=60°,OC=OB=2,
∴
=,
故答案为:.
18.
【分析】由图可知:阴影部分的面积=半圆CAB的面积-△ABC的面积+扇形ABC的面积-△ABC的面积,可根据各自的面积计算方法求出面积即可.
解:∵等腰中,
∴BC=2
∴S扇形ACB,S半圆CABπ×(1)2,S△ABC=1;
所以阴影部分的面积=S半圆CAB-S△ABC+S扇形ACB-S△ABC .
故答案是:.
三、解答题
19.
(1)证明:由旋转性质得:
是等边三角形
所以
∴;
(2)依题意得:AB=BD=4,BC=BE=1,
所以A,C两点经过的路径长之和为.
20.
解:(1)设∠AOC=n°,
∵AC=R,
∴R,
∴n=60°,
∴∠AOC=60°;
(2)∵∠AOC=60°,OA=OC,
∴△AOC是等边三角形,
∴∠ACO=∠AOC=60°.
∵△AEC≌△DEO,
∴∠CAO=∠DOB=∠C=60°,
∴AC∥OD,
∴∠BOD=∠CAO=60°, ∠COD=∠C=60°,
∴D是劣弧BC的中点,
∴D的位置,只要满足∠DOB=60°,或AC∥OD或劣弧BC的中点即可.
21.
解:
如图,以OB为直径画⊙K交AB于T,连接TK,图中的优弧,即为点E的运动轨迹.
∵△ABC是等边三角形,
∴∠OBA=∠OBC=30°,
∴∠TKO=60°,
∵AB=BC=AC=,
∴OB=2,
∴KO=1,
∴点E经过的路径长为.
22.
解:(1)证明:连接,
,
,
∵AB=AC,
∴∠ABC=∠ACB.
∴∠ODB=∠ACB,
∴OD∥AC.
∵DF是⊙O的切线,
∴DF⊥OD.
∴DF⊥AC.
(2)连接OE,
∵DF⊥AC,∠CDF=22.5°.
∴∠ABC=∠ACB=67.5°,
∴∠BAC=45°.
∵OA=OE,
∴∠AOE=90°.
的半径为4,
,,
.
23.
解:(1)△AB′C′如图所示:
(2)由图可知,AC=2,
∴线段AC旋转过程中扫过的扇形的面积.
24.
(1)证明:∵AB为⊙O的直径,
∴AC⊥BC
又∵OF⊥AC
∴OF∥BC
(2)证明:∵AB⊥CD
∴
∴∠CAB=∠BCD
又∵∠AFO=∠CEB=90°,OF=BE,
∴△AFO≌△CEB
(3)连接DO.设OE=x,
∵AB⊥CD
∴CE=CD=5cm.
在△OCB中,OC=OB=x+5(cm),
根据勾股定理可得:(x+5)2=(5)2+x2
解得:x=5,即OE=5cm,
∴tan∠COE=,
∴∠COE=60°
∴∠COD=120°,
∴扇形COD的面积是:cm2
△COD的面积是:CD OE=×10×5=25cm2
∴阴影部分的面积是:()cm2.
一、单选题
1.如图,将⊙O沿弦AB折叠,恰好经过圆心O,若⊙O的半径为3,则的长为( )
A. B. C. D.
2.一个扇形的弧长是,其圆心角是150°,此扇形的面积为( )
A. B. C. D.
3.一个扇形的弧长是12πcm,面积是108πcm2,则此扇形的圆心角的度数是( )
A.300° B.150° C.120° D.75°
4.如图,扇形OBA中,点C在弧AB上,连接BC,P为BC中点.若,,则点C沿弧从点B运动到点A的过程中,点P所经过的路径长为( )
A. B. C. D.6
5.如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接.若,则图中阴影部分的面积是( )
A. B. C. D.
6.如图,中,,,BO=2cm,将绕点O逆时针旋转至,点在BO的延长线上,则边BC扫过区域(图中阴影部分)的面积为( )
A. B. C. D.
7.如图,在正三角形ABC中,边长,将正三角形ABC绕点A按逆时针方向旋转180°至正三角形,则线段BC扫过的面积为( )
A. B. C. D.
8.如图是一张圆心为O,半径为4cm的圆形纸片,沿弦AC所在直线折叠,使得经过点O,将纸片展平后,作半径,则图中阴影部分的面积等于( )
A. B.
C. D.
9.如图,在矩形ABCD中,AC为对角线,,,以B为圆心,AB长为半径画弧,交AC于点M,交BC于点N,则阴影部分的面积为( )
A. B. C. D.
10.如图,两个半径长均为的直角扇形的圆心分别在对方的圆弧上,扇形的圆心C是的中点,且扇形绕着点C旋转,半径,交于点G,半径,交于点H,则图中阴影面积等于( )
A. B. C. D.
二、填空题
11.如图,AB是⊙O的直径,BC是⊙O的弦,先将沿BC翻折交AB于点D,再将沿AB翻折交BC于点E.若,AB=4,则的长度为 _____.
12.如图,在扇形ODE中,,,是扇形的内接三角形,其中A、B、C分别在弧DE和半径OE、OD上,,,则线段AC的最小值为______.
13.如果一个扇形的半径是2,弧长是,则此扇形的图心角的度数为____.
14.如图,正方形 ABCD 的边长为4cm,动点M,N分别从点A,C同时出发,以相同的速度分别沿 AB,CD向终点 B,D移动,当点 M到达点B时,运动停止.过点B作直线MN的垂线BG,垂足为点G,则G点运动的路径长为_______cm
15.如图,边长为4的正方形ABCD的对角线交于点O,以OC为半径的扇形的圆心角.则图中阴影部分面积是_____.
16.如图,在中,,,,将三角形绕点按逆时针方向旋转()后得到三角形,点经过的路径为弧,则图中阴影部分的面积是_________.
17.如图,AB是⊙O的直径,CD为弦,AB⊥CD,若,CB=2,则阴影部分的面积是______.
18.如图,等腰中,,以A为圆心,以AB为半径作﹔以BC为直径作.则图中阴影部分的面积是______.(结果保留)
三、解答题
19.如图,将绕点B顺时针旋转60度得到,点C的对应点E恰好落在AB的延长线上,连接AD.
(1)求证:;
(2)若AB=4,BC=1,求A,C两点旋转所经过的路径长之和.
20.如图,在⊙O中,AB是直径,半径为R,弧AC=R.
求:(1)∠AOC的度数.(2)若D为劣弧BC上的一动点,且弦AD与半径OC交于E点.试探求△AEC≌△DEO时,D点的位置.
21.如图,边长为的等边△ABC内接于⊙O,D为劣弧上一点,过点B作BE⊥OD于点E,当点D从点B沿劣弧运动到点C时,求点E经过的路径长.
22.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
23.如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°
(1)画出旋转之后的△AB′C′;
(2)求线段AC旋转过程中扫过的扇形的面积.
24.如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1)求证:OF∥BC;
(2)求证:△AFO≌△CEB;
(3)若EB=5cm,CD=cm,设OE=x,求x值及阴影部分的面积.
答案
一、单选题
1.C
【分析】连接OA、OB,作OC⊥AB于C,根据翻转变换的性质得到OC=OA,根据等腰三角形的性质、三角形内角和定理求出∠AOB,根据弧长公式计算即可.
解:连接OA、OB,作OC⊥AB于C,
由题意得,OC=OA,
∴∠OAC=30°,
∵OA=OB,
∴∠OBA=∠OAC=30°,
∴∠AOB=120°,
∴劣的长==2π,
故选:C.
2.B
【分析】先求出该扇形的半径,再求其面积即可;
解:该扇形的半径为:,
∴扇形的面积为:,
故选:B.
3.C
【分析】先根据扇形面积公式求出半径,再根据弧长公式解答即可.
解:设扇形所在的圆的半径为rcm,圆心角为n°,由题意得:,解得:r=18,
∵,
∴此扇形的圆心角n=120°.
故选:C.
4.B
【分析】连接OC、OP,易得∠OPB=90°,点P是在以OB的中点D为圆心,BD为半径的圆上运动,求即可.
解:连接OC、OP,
∵OB=OC,
∴△BOC为等腰三角形,
∵P为BC中点,
∴OP⊥BC(三线合一),
即∠OPB=90°,
∴点P是在以OB的中点D为圆心,BD为半径的圆上运动,如图所示,
当点C运动到点A时,点P到达位置,
点P所经过的路径长为,
连接,∵D为OB中点,为AB中点,
∴∥OA,
∴=,BD=OA=3,
∴,
即点P所经过的路径长为 ,
故选:B.
5.B
【分析】连接CO,且直线l与AO交于点D,解直角三角形求出,即可求出扇形的面积,再算出的面积,即可求出阴影部分面积.
解:连接CO,且直线l与AO交于点D,如图所示,
∵扇形中,,
∴,
∵点A与圆心O重合,
∴,,
∴,
∴,
由勾股定理得:,
∵,,
∴,
故选:B.
6.A
【分析】先在Rt△OCB中利用特殊角求出OC、BC、∠COB,进而可求出,接着可以求出,则可以表示出、、,则阴影部分的面积可求.
解:在Rt△OCB中,∠CBO=30°,BO=1,
∴∠COB=60°,2OC=BO=BC,
∴,BC=,OC=1,
∴,
∴,
根据旋转的性质可知,,,,
∴,,,
∴,
∴(cm2),
故选:A.
7.B
【分析】分别取BC,的中点为D,,把所求面积分解成三部分在进行求解即可;
解:如图,BC扫过的面积即为阴影部分的面积;
分别取BC,的中点为D,,
∴,
∵等于大半圆面积减去小半圆面积,,
∴,
∵是所对弓形的面积的一半,
∴,
∴,
∴;
故选B.
8.A
【分析】作OD⊥AC交圆于点D、交AC于点E,根据垂径定理,OD平分 和,又因为AC是对折线,所以OD与AC互相垂直平分,所以ODCO组成的图形面积是与组成的图形面积的一半,也就等于ADCEA组成图形面积,此部分面积可用扇形OAC的面积减去△OAC面积求出,再用求出的面积减去扇形ODB的面积即得阴影部分面积.
解:作OD⊥AC交圆于点D,交AC于点E,连接OC,如图,
∴OD垂直平分弦AC,平分 和,
∵AC是向圆内的折线,且弦AC折叠后经过点O,
∴点O是点D关于AC的对称点,即OD与AC互相垂直平分,
∴OE=DE=OD
设与弦AC构成的图形面积为SADC,与构成的图形面积为SADCO,与和线段OD构成的图形面积为SODC,
则SADC=SADCO,SODC=SADCO,
∴SODC=SADC,
∵OD、OA都是圆O的半径,半径为4cm,
∴OE=OD=OA=,
∴∠OAE=30°,
∴∠AOE=90°-30°=60°,
∴∠AOC=2∠AOE=2×60°=120°,
∴S扇形OAC==(cm2),
∵AC=2AE=cm,
∴S△OAC=(cm2),
∴SADC= S扇形OAC - S△OAC=()(cm2),
∴SODC=()(cm2),
∵OB⊥OA,∠AOE=60°,
∴∠BOD=∠AOB-∠AOE=90°-60°=30°,
∴S扇形OBD=(cm2),
∴S阴影=SODC- S扇形OBD==()(cm2),
故选 A.
9.A
【分析】连接BM,过M作MH⊥BC于H,由∠ACB=30°得到∠BAC=60°,求得△ABM是等边三角形,得到∠ABM=60°,推出∠MBN=30°,根据三角形和扇形的面积公式即可得到结论.
解:连接BM,过M作MH⊥BC于H,
在矩形ABCD中,∠ABC=90°,
∵AB=1,∠ACB=30°,
∴∠BAC=60°,AC=2AB=2,BC=,
∵BA=BM,
∴△ABM是等边三角形,
∴∠ABM=60°,
∴∠MBN=30°,
∴MH=BM=,
∴S阴=S△BCM-S扇形BMN==,
故选:A.
10.D
【分析】先根据扇形面积公式求出两扇形面积,再过C分别作CM⊥AE于M,CN⊥BE于N,连接EC,再证明△CMG≌△CNH,可证得白色部分的面积等于对角线为的正方形CMEN得面积,进而可求得阴影部分的面积.
解:∵两个直角扇形的半径长均为,
∴两个扇形面积和为,
过C分别作CM⊥AE于M,CN⊥BE于N,连接EC,则四边形CMEN是矩形,
∵C是的中点,
∴∠AEC=∠BEC,即EC平分∠AEB,
∴CM=CN,
∴四边形CMEN是正方形,
∴∠CMG=∠MCN=∠CNH,
∴∠MCG+∠GCN=∠NCH+∠GCN=90°,
∴∠MCG=∠NCH,
∴△CMG≌△CNH(ASA),
∴白色部分的面积等于对角线为的正方形CMEN的面积,
∴空白部分面积为,
∴阴影部分面积为,
故选:D.
二、填空题
11.
【分析】由同圆或等圆中相等的圆周角所对的弧相等可得,因此.结合AB是的直径,可得所对的圆心角的度数.再利用弧长公式计算的长即可.
解:∵、、、所在的圆是等圆
又∵、、所对的圆周角都是
∴==
又∵=
∴===
又∵ +++=
∴=
∴
又∵AB是的直径
∴所对的圆心角为
∴的长=
故答案为
12.
【分析】取BC的中点M,连接AM,OM,AO.AM+OM≥OA,当且仅当A、M、O三点共线时等号成立,这样问题迎刃而解.
解:取BC的中点M,连接AM,OM,AO.
∵AC:BC=3:8,
∴可以假设AC=3k,BC=8k,则CM=BM=4k,
∵∠ACB=∠COB=90°,
∴
∵AM+OM≥OA,
∴5k+4k≥5,
∴k≥,
∴k的最小值为,
∴AC的最小值为,
故答案为.
13.45°
【分析】直接利用扇形弧长公式代入求出即可.
解:∵扇形的弧长是,半径为2,
∴,
解得:n=45,
故答案为:45°.
14.
【分析】连接BD,AC相交于O,在运动过程中,,得到点G的轨迹为以OB 为直径的半圆,G点轨迹长度等于半圆弧长,即可算出.
解:连接BD,AC相交于O
在运动过程中,
故点G的轨迹为以OB为直径的半圆
G点轨迹长度等于半圆弧长,
即:
故答案为:.
15.
【分析】证明△OCG≌△OBE,经过观察易得出结论:阴影部分面积=扇形面积-正方形面积的.
解:∵四边形ABCD为正方形,
∴OB=OC,∠BOC=90°,∠OBE=∠OCG=45°,
∵扇形的圆心角,
∴∠BOC-∠COE=∠FOH-∠COE,即∠BOE=∠COG,
在△OCG和△OBE中,
∠OBE=∠OCG,∠BOE=∠COG, OB=OC
∴△OCG≌△OBE,
∵正方形边长为4,
∴AC=,
∴OC=
∵,
=
=
=
故答案为:
16.
【分析】把△ADE顺时针方向旋转60°到△ABC,要求的阴影部分的面积就是边长为5,角为60°的扇形面积.
解:圆形面积= =25π
扇形的面积= =
17.
【分析】连接OC,设CD与AB的交点为E,利用垂径定理、勾股定理判定△OBC是等边三角形,运用扇形的面积减去△OBC的面积即可.
解:连接OC,设CD与AB的交点为E,
∵AB是⊙O的直径,AB⊥CD,,CB=2,
∴,,
∴∠ECB=30°,∠CBE=60°,
∵CO=BO,
∴△OBC是等边三角形,
∴∠BOC=60°,OC=OB=2,
∴
=,
故答案为:.
18.
【分析】由图可知:阴影部分的面积=半圆CAB的面积-△ABC的面积+扇形ABC的面积-△ABC的面积,可根据各自的面积计算方法求出面积即可.
解:∵等腰中,
∴BC=2
∴S扇形ACB,S半圆CABπ×(1)2,S△ABC=1;
所以阴影部分的面积=S半圆CAB-S△ABC+S扇形ACB-S△ABC .
故答案是:.
三、解答题
19.
(1)证明:由旋转性质得:
是等边三角形
所以
∴;
(2)依题意得:AB=BD=4,BC=BE=1,
所以A,C两点经过的路径长之和为.
20.
解:(1)设∠AOC=n°,
∵AC=R,
∴R,
∴n=60°,
∴∠AOC=60°;
(2)∵∠AOC=60°,OA=OC,
∴△AOC是等边三角形,
∴∠ACO=∠AOC=60°.
∵△AEC≌△DEO,
∴∠CAO=∠DOB=∠C=60°,
∴AC∥OD,
∴∠BOD=∠CAO=60°, ∠COD=∠C=60°,
∴D是劣弧BC的中点,
∴D的位置,只要满足∠DOB=60°,或AC∥OD或劣弧BC的中点即可.
21.
解:
如图,以OB为直径画⊙K交AB于T,连接TK,图中的优弧,即为点E的运动轨迹.
∵△ABC是等边三角形,
∴∠OBA=∠OBC=30°,
∴∠TKO=60°,
∵AB=BC=AC=,
∴OB=2,
∴KO=1,
∴点E经过的路径长为.
22.
解:(1)证明:连接,
,
,
∵AB=AC,
∴∠ABC=∠ACB.
∴∠ODB=∠ACB,
∴OD∥AC.
∵DF是⊙O的切线,
∴DF⊥OD.
∴DF⊥AC.
(2)连接OE,
∵DF⊥AC,∠CDF=22.5°.
∴∠ABC=∠ACB=67.5°,
∴∠BAC=45°.
∵OA=OE,
∴∠AOE=90°.
的半径为4,
,,
.
23.
解:(1)△AB′C′如图所示:
(2)由图可知,AC=2,
∴线段AC旋转过程中扫过的扇形的面积.
24.
(1)证明:∵AB为⊙O的直径,
∴AC⊥BC
又∵OF⊥AC
∴OF∥BC
(2)证明:∵AB⊥CD
∴
∴∠CAB=∠BCD
又∵∠AFO=∠CEB=90°,OF=BE,
∴△AFO≌△CEB
(3)连接DO.设OE=x,
∵AB⊥CD
∴CE=CD=5cm.
在△OCB中,OC=OB=x+5(cm),
根据勾股定理可得:(x+5)2=(5)2+x2
解得:x=5,即OE=5cm,
∴tan∠COE=,
∴∠COE=60°
∴∠COD=120°,
∴扇形COD的面积是:cm2
△COD的面积是:CD OE=×10×5=25cm2
∴阴影部分的面积是:()cm2.
同课章节目录
