九年级数学上册试题 第三章《圆的基本性质》全章复习-浙教版(含解析)
文档属性
| 名称 | 九年级数学上册试题 第三章《圆的基本性质》全章复习-浙教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 07:55:47 | ||
图片预览


文档简介
第三章《圆的基本性质》全章复习
一、单选题
1.下列关于圆的说法,正确的是( )
A.弦是直径,直径也是弦
B.半圆是圆中最长的弧
C.圆的每一条直径所在的直线都是它的对称轴
D.过三点可以作一个圆
2.如图,在等边△ABC中,D是AC的中点,则点D与以AB为直径的⊙O的位置关系是( )
A.圆上 B.圆内 C.圆外 D.不能确定
3.如图,线段AB是⊙O的直径,弦CD⊥AB,BC=OD=2,DC的长等于( )
A.2 B.4 C. D.2
4.如图,在半径为5的中,弦BC,DE所对的圆心角分别是,.若,,则弦BC的弦心距为( ).
A. B. C.4 D.3
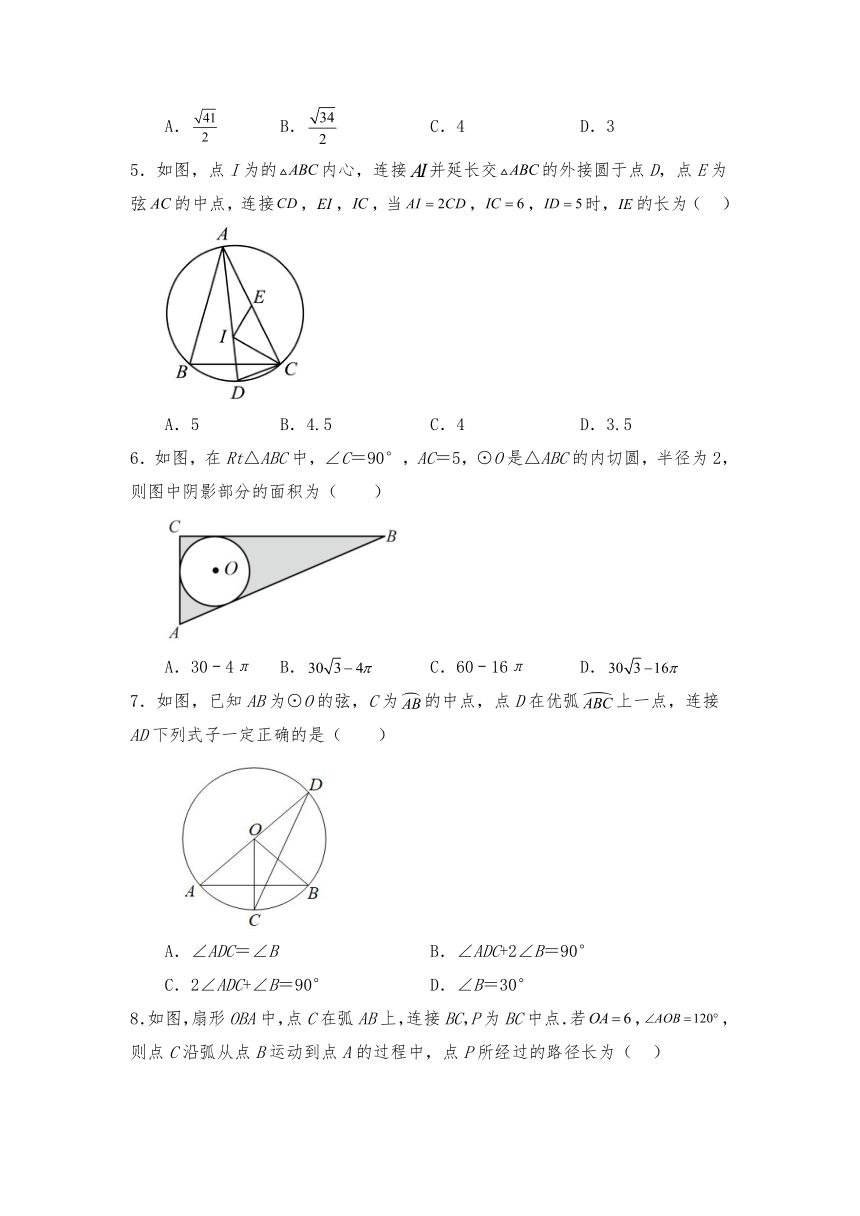
5.如图,点I为的内心,连接并延长交的外接圆于点D,点E为弦的中点,连接,,,当,,时,的长为( )
A.5 B.4.5 C.4 D.3.5
6.如图,在Rt△ABC中,∠C=90°,AC=5,⊙O是△ABC的内切圆,半径为2,则图中阴影部分的面积为( )
A.30﹣4π B. C.60﹣16π D.
7.如图,已知AB为⊙O的弦,C为的中点,点D在优弧上一点,连接AD下列式子一定正确的是( )
A.∠ADC=∠B B.∠ADC+2∠B=90°
C.2∠ADC+∠B=90° D.∠B=30°
8.如图,扇形OBA中,点C在弧AB上,连接BC,P为BC中点.若,,则点C沿弧从点B运动到点A的过程中,点P所经过的路径长为( )
A. B. C. D.6
9.如图,将两个正方形如图放置(B,C,E共线,D,C,G共线),若AB=3,EF=2,点O在线段BC上,以OF为半径作⊙O,点A,点F都在⊙O上,则OD的长是( )
A.4 B. C. D.
10.如图,C为半圆内一点,O为圆心,直径长为,,将绕圆心O逆时针旋转至,点在上,则边扫过区域(图中阴影部分)的面积为( )
A. B. C. D.
二、填空题
11.如图,的半径为13,,分别以点A,B为圆心,大于的长为半径作弧,两弧相交于点M,N,作直线交于点C,则________.
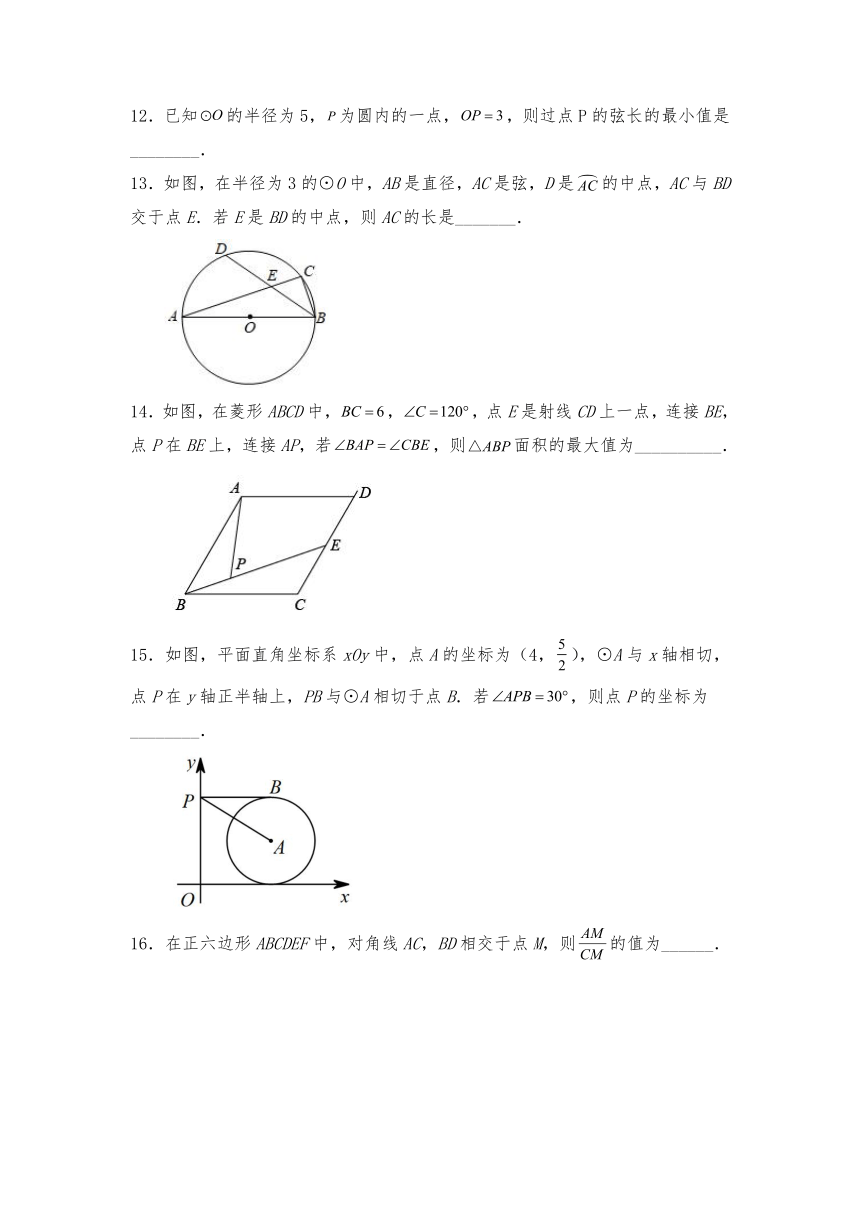
12.已知的半径为5,为圆内的一点,,则过点P的弦长的最小值是________.
13.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是_______.
14.如图,在菱形ABCD中,,,点E是射线CD上一点,连接BE,点P在BE上,连接AP,若,则面积的最大值为__________.
15.如图,平面直角坐标系xOy中,点A的坐标为(4,),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若,则点P的坐标为________.
16.在正六边形ABCDEF中,对角线AC,BD相交于点M,则的值为______.
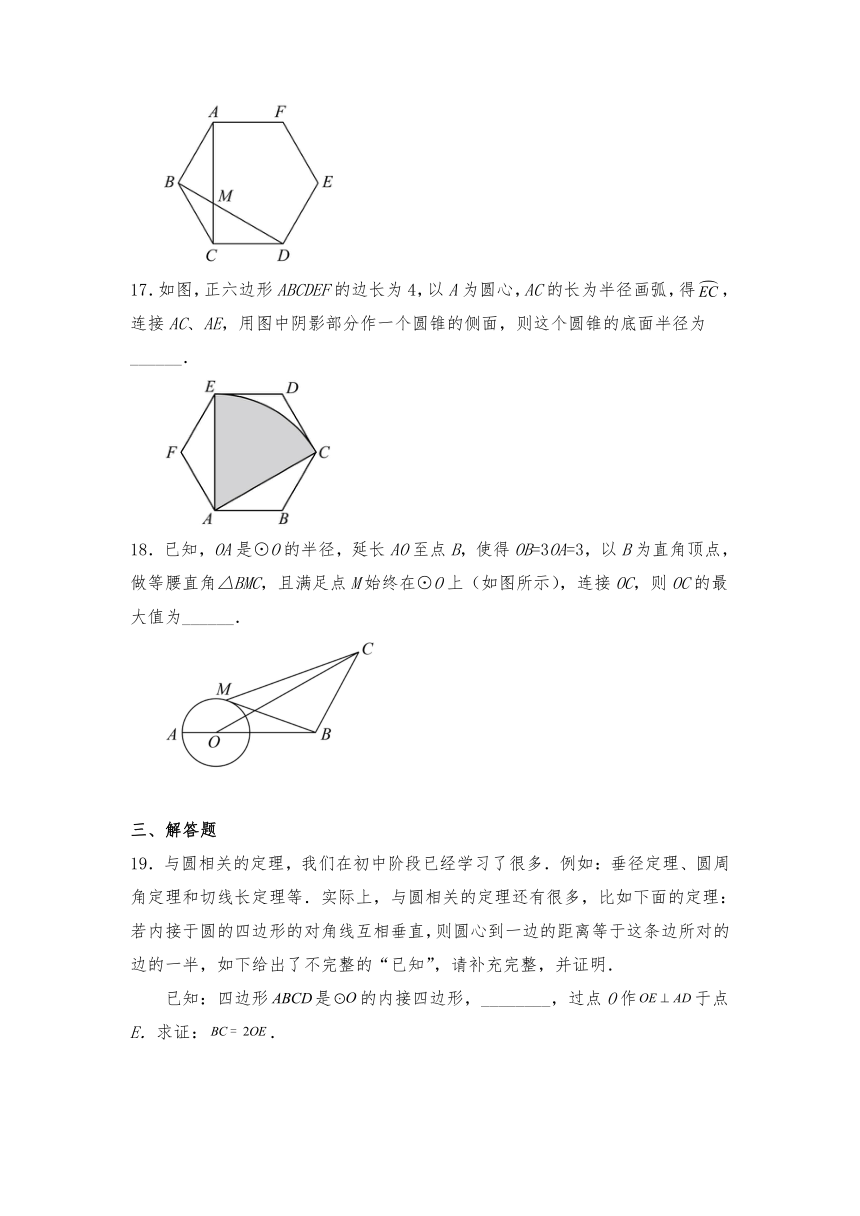
17.如图,正六边形ABCDEF的边长为4,以A为圆心,AC的长为半径画弧,得,连接AC、AE,用图中阴影部分作一个圆锥的侧面,则这个圆锥的底面半径为______.
18.已知,OA是⊙O的半径,延长AO至点B,使得OB=3OA=3,以B为直角顶点,做等腰直角△BMC,且满足点M始终在⊙O上(如图所示),连接OC,则OC的最大值为______.
三、解答题
19.与圆相关的定理,我们在初中阶段已经学习了很多.例如:垂径定理、圆周角定理和切线长定理等.实际上,与圆相关的定理还有很多,比如下面的定理:若内接于圆的四边形的对角线互相垂直,则圆心到一边的距离等于这条边所对的边的一半,如下给出了不完整的“已知”,请补充完整,并证明.
已知:四边形是的内接四边形,________,过点O作于点E.求证:.
20.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
21.已知是的直径,弦与相交,.
(Ⅰ)如图①,若为的中点,求和的大小;
(Ⅱ)如图②,过点作的切线,与的延长线交于点,若,求的大小.
22.如图,AB是⊙O的直径,点C是⊙O上的一点,OD⊥AB交AC于点E,∠D=2∠A.
(1) 求证:CD是⊙O的切线;
(2) 求证:DE=DC;
(3) 若OD=5,CD=3,求AE的长.
23.如图,正方形的边长为4,以为直径在正方形内部作半圆O,点E在边上,,连接,和.
(1) 求证:是半圆O的切线;
(2) 请直接写出图中阴影部分的面积(用含π的代数式表示).
24.阅读与思考:阿基米德(公元前287年-公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家、静态力学和流体静力学的奠基人,并且享有“力学之父”的美称,留给后人的最有价值的书是《阿基米德全集》.在该书的“引理集”中有这样一道题:
如图1,以为直径作半圆O,弦是一个内接正五边形的一条边(即:),点D是的中点,连接并延长与直径的延长线交于点E,连接交于点F,过点F作于点M.求证:是半圆的半径.
下面是勤奋小组的部分证明过程:
证明:如图2,过点D作于点H.
∵,
∴.(依据1)
∵点D是的中点,
∴.
∵,
∴.
∴.(依据2)
∵以为直径作半圆O,
∴.(依据3)
∴.
∵四边形是半圆O的内接四边形,
∴.(依据4)
∵,
∴.
∵于点M,
∴.
∵,
∴.
∵.
∵.
∴.
∴.
……
通过上面的阅读,完成下列任务:
(1)任务一:直接写出依据1,依据2,依据3和依据4;
(2)任务二:根据勤奋小组的解答过程完成该题的证明过程.(提示:先求出的度数,再根据等腰三角形的性质或判定完成该题的证明过程)
答案
一、单选题
1.C
【分析】根据弧、弦的概念、对称轴的概念、过三点的圆的条件判断即可.
解:A、弦不一定是直径,但直径是弦,本选项说法错误,不符合题意;
B、半圆小于优弧,半圆是圆中最长的弧说法错误,本选项不符合题意;
C、圆的每一条直径所在的直线都是它的对称轴,本选项说法正确,符合题意;
D、过不在同一直线上的三点可以作一个圆,本选项说法错误,不符合题意;
故选:C.
2.A
【分析】根据题意可知,的中点为点,连接,先根据等边三角形的性质可得,再根据三角形中位线定理可得,从而可得为的半径,由此即可得.
解:如图,由题意可知,的中点为点,连接,
是等边三角形,
,
是的中点,为的中点,
,
,
即为的半径,
点在上,
故选:A.
3.D
【分析】如图,令、的交点为,由垂径定理得,证明,则,,在中,由勾股定理得,求出的值,根据计算求解的值即可.
解:如图,令、的交点为,
∵,是的直径,
∴,
在和中,
∵,
∴,
∴,
∴,
在中,由勾股定理得,
∴,
故选D.
4.D
【分析】作AH⊥BC于H,作直径CF,连接BF,先利用等角的补角相等得到∠DAE=∠BAF,再利用圆心角、弧、弦的关系得到DE=BF=6,由AH⊥BC,根据垂径定理得CH=BH,则AH为△CBF的中位线,然后根据三角形中位线性质得到AH=BF=3.
解:作AH⊥BC于H,作直径CF,连接BF,如图,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴,
∴DE=BF=6,
∵AH⊥BC,
∴CH=BH,
而CA=AF,
∴AH为△CBF的中位线,
∴AH=BF=3,
故选:D.
5.C
【分析】延长ID到M,使DM=ID,连接CM.想办法求出CM,证明IE是△ACM的中位线即可解决问题.
解:延长ID到M,使DM=ID,连接CM.
∵I是△ABC的内心,
∴∠IAC=∠IAB,∠ICA=∠ICB,
∵∠DIC=∠IAC+∠ICA,∠DCI=∠BCD+∠ICB,
∴∠DIC=∠DCI,
∴DI=DC=DM,
∴∠ICM=90°,
∴CM==8,
∵AI=2CD=10,
∴AI=IM,
∵AE=EC,
∴IE是△ACM的中位线,
∴IE=CM=4,
故选:C.
6.A
【分析】先由切线长定理和勾股定理算出三角形另外两边的长,再根据图中阴影部分的面积=△ABC的面积-⊙O的面积,然后利用三角形的面积公式和圆的面积公式计算即可.
解:过点O作AB、AC、BC的垂线,垂足分别为D、E、F,如图,
,
∴四边形CEOF是矩形,
,
∴四边形CEOF是正方形,
,
∵⊙O是△ABC的内切圆,
,
设,
在中,,
,
解得,
,
.
故选A.
7.C
【分析】先利用垂径定理,由C为的中点得到OC⊥AB,则∠A+∠AOC=90°,然后根据圆周角定理得到∠AOC=2∠ADC,加上∠A=∠B,于是可判断C选项一定正确.
解:∵C为的中点,
∴OC⊥AB,
∴∠A+∠AOC=90°,
∵∠AOC=2∠ADC,
∴2∠ADC+∠A=90°,
∵OA=OB,
∴∠A=∠B,
∴∠2ADC+∠B=90°.
故选:C.
8.B
【分析】连接OC、OP,易得∠OPB=90°,点P是在以OB的中点D为圆心,BD为半径的圆上运动,求即可.
解:连接OC、OP,
∵OB=OC,
∴△BOC为等腰三角形,
∵P为BC中点,
∴OP⊥BC(三线合一),
即∠OPB=90°,
∴点P是在以OB的中点D为圆心,BD为半径的圆上运动,如图所示,
当点C运动到点A时,点P到达位置,
点P所经过的路径长为,
连接,∵D为OB中点,为AB中点,
∴∥OA,
∴=,BD=OA=3,
∴,
即点P所经过的路径长为 ,
故选:B.
9.B
【分析】连接OA,OF,由题意得OA=OF,设OC=x,由勾股定理得,解答方程可得OC的值,再运用勾股定理可得OD的长.
解:连接OA,OF,如图,
∵OF是半圆O的半径,
∴OA=OF,
∵四边形ABCD、EFGC是正方形,
∴,
设,
∴BO=BC-OC=3-x,OE=OC+CE=x+2,
在Rt和Rt中,
,
∴,
∵
∴,
解得,,即OC=1,
在Rt中,,
∴,
故选:B.
10.B
【分析】根据已知条件和旋转的性质得出两个扇形的圆心角的度数,再根据扇形的面积公式进行计算即可得出答案.
解:∵∠BOC=60°,△B′OC′是△BOC绕圆心O逆时针旋转得到的,
∴∠B′OC′=60°,△BCO=△B′C′O,
∴∠B′OC=60°,∠C′B′O=30°,
∴∠B′OB=120°,
∵AB=2cm,
∴OB=1cm,OC′=cm,
∴B′C′=cm,
∴S扇形B′OB= cm2,
S扇形C′OC= cm2,
∴阴影部分面积=S扇形B′OB+S△B′C′O-S△BCO-S扇形C′OC=S扇形B′OB-S扇形C′OC=cm2;
故选:B.
二、填空题
11.12
【分析】连接OC、OB,根据作图可知OC是线段AB的垂直平分线,则有BC=AC=AB.在Rt△BOC中,利用勾股定理即可求解OC.
解:连接OC、OB,如图,
根据作图可知,OC是线段AB的垂直平分线,
则有BC=AC=AB=10×=5,
又∵圆的半径OB=13,
∴在Rt△BOC中,利用勾股定理可得:,
故答案为:12.
12.8
【分析】过P点作弦AB,使AB⊥OP,则AB为过P点的最短的弦,连结OA,根据垂径定理得AP=BP,在Rt△AOP中,根据勾股定理可计算出AP=4,则AB=2AP=8.
解:过P点作弦AB,使AB⊥OP,则AB为过P点的最短的弦,
连结OA,
∵OP⊥AB,
∴AP=BP,
在Rt△AOP中,OA=5,OP=3,
∴AP=,
∴AB=2AP=8.
故答案为:8.
13.
【分析】连接OD,交AC于F,根据垂径定理的推论得出OD⊥AC,AF=CF,进而证得DF=BC,根据三角形中位线定理求得OF=BC=DF,从而求得BC=DF,利用勾股定理即可求得AC.
解:如图,连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中,
,
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,AB=2OD=6,
∴BC=2,
∴.
故答案为:.
14.
【分析】若要使的面积最大,底AB固定,故只要AB边上的高最大时,即三角形面积最大;可证,故可知点P在△APB的外接圆的劣弧上,当点P在劣弧的中点处,△APB的面积最大,求出AB边上的高即可求解.
解:∵四边形ABCD是菱形,
∴AB=BC=6,AB//CD,
∴
∵,
∴ 即,
∵,
∴,
∵,
∴点P在在△APB的外接圆上,
若要使的面积最大,底AB固定,,故只要AB边上的高最大时,即三角形面积最大;此时点P在劣弧的中点处,如图,
设点O为△APB的外接圆的圆心,OP⊥AB于点F,
∴,,
∴
∴
由勾股定理得,
∴
∴PF=
∴
即面积的最大值为.
故答案为:.
15.(0,)
【分析】连接AB,过点A分别作AC⊥x轴、AD⊥y轴,利用根据圆的切线性质可知△PAB、△AOC为直角三角形,AB=AC=,利用直角三角形中30°角的性质和勾股定理分别求出AP、AD的长度,进而求出OD、PD的长度即可求得答案.
解:如图,过点A分别作AC⊥x轴于点C、AD⊥y轴于点D,连接AB,
∵AD⊥y轴,AC⊥x轴,
∴四边形ADOC为矩形.
∴AC=OD,OC=AD.
∵⊙A与x轴相切,
∴AC为⊙A的半径.
∵点A坐标为(4,),
∴AC=OD=,OC=AD=4,
∵PB是切线,
∴AB⊥PB.
∵∠APB=30°,
∴PA=2AB=5.
在Rt△PAD中,根据勾股定理,得,
∴OP=PD+DO=.
∵点P在y轴的正半轴上,
∴点P坐标为(0,).
故答案为:(0,).
16.2
【分析】根据多边形的内角和公式即可得出∠ABC,∠BCD的度数,再根据等腰三角形的性质证明,设 则则 从而可得答案.
解:∵六边形ABCDEF是正六边形,
∴∠BCD=∠ABC= (6-2)×180°=120°,AB=BC=CD,
∴∠BAC=∠ACB=∠CBD=∠CDB=(180°-120°)=30°,
∠ABM =90°,
设 则
故答案为2.
17.
【分析】由正六边形ABCDEF的边长为4,可得AB=BC=4,∠ABC=∠BAF=120°,进而求出∠BAC=30°,∠CAE=60°,过B作BHAC于H,由等腰三角形的性质和含30°直角三角形的性质得到AH=CH=AC,BH=2.在RtABH中,由勾股定理求得AH=,得到.根据扇形的面积公式可得到阴影部分的面积,即是圆锥的侧面积,最后根据圆锥的侧面积公式求解底面半径即可.
解:∵正六边形ABCDEF的边长为4,
∴AB=BC=4,
,
∵∠ABC+∠BAC+∠BCA=180°,
∴,
如图,过B作BHAC于H,
∴AH=CH=AC,
,
在RtABH中,
,
∴,
同理可求∠EAF=30°,
∴,
∴,
∴,
∵,
∴,
∴r=,
故答案为:.
18.或
【分析】由“SAS”可证△NBM≌△OBC,可得MN=OC,则当点O在线段MN上时,MN有最大值,即可求解.
解:如图,过点B作BN⊥AB,且BN=OB,连接ON,OM,MN,
∴∠NBO=90°=∠MBC,
∴∠MBN=∠OBC,
在△NBM和△OBC中,
∵MB=BC,∠MBN=∠OBC,BN=OB,
∴△NBM≌△OBC(SAS),
∴MN=OC,
∵MN≤OM+ON,
∴当点O在线段MN上时,MN有最大值,
∵OB=3OA=3,
∴,
∴MN的最大值为,
∴OC的最大值为,
故答案为:
三、解答题
19.
证明:连接并延长交于点F,连接,如图所示,
∵为直径,
∴,即,
又∵,
∴,
∵,
∴,
∴是的中位线,
∴,
∵,
∴,
∴,
∴.
20.
(1)证明:如答图,过点O作OE⊥AB于点E,
∵AE=BE,CE=DE,
∴BE﹣DE=AE﹣CE,
即AC=BD
(2)由(1)可知,OE⊥AB且OE⊥CD,
连接OC,OA,
∵OA=10,OC=8,OE=6,
∴.
∴AC=AE﹣CE=8﹣.
21.
解:(Ⅰ)∵是的直径,∴.
∴.
又∴,∴.
由为的中点,得.
∴.
∴.
(Ⅱ)如图,连接.
∵切于点,
∴,即.
由,又,
∴是的外角,
∴.
∴.
又,得.
∴.
22.
(1)证明:连接OC,如图,
∵OA=OC,
∴∠ACO=∠A,
∴∠COB=∠A+∠ACO=2∠A,
又∵∠D=2∠A,
∴∠D=∠COB.
又∵OD⊥AB,
∴∠COB+∠COD=90°,
∴∠D+∠COD=90°,即∠DCO=90°,
∴OC⊥DC,
又点C在⊙O上,
∴CD是⊙O的切线;
(2)证明:∵∠DCO=90°,
∴∠DCE+∠ACO=90°,
又∵OD⊥AB,
∴∠AEO+∠A=90°,
又∵∠A=∠ACO,∠DEC=∠AEO,
∴∠DEC=∠DCE,
∴DE=DC;
(3)解:∵∠DCO=90°,OD=5,DC=3,
∴OC===4,
∴OA=OC=4,
又DE=DC=3,
∴OE=OD﹣DE=2,
在Rt△AEO中,由勾股定理得:,
∴AE=2.
23.
(1)解:过点O作OF⊥DE于F,如图所示:
在中,,,CE=BC-BE=4-1=3,
,
在中,,,
,
在中,,,
,
,
三角形是直角三角形,且,
,
,
,
是圆的半径,且,
是半圆O的切线.
(2).
24.
(1)解:依据1:一条弧所对的圆周角等于它所对圆心角度数的一半(或圆周角定理);
依据2:同弧或等弧所对的圆周角相等;
依据3:直径所对的圆周角是直角;
依据4:圆内接四边形的对角互补;
(2)解:∵,
∴,
∵于点H,
∴,
∴,
∵是的外角,
∴,
∴,
∴,
∴,
∴,
∴,
∴是半圆的半径.
一、单选题
1.下列关于圆的说法,正确的是( )
A.弦是直径,直径也是弦
B.半圆是圆中最长的弧
C.圆的每一条直径所在的直线都是它的对称轴
D.过三点可以作一个圆
2.如图,在等边△ABC中,D是AC的中点,则点D与以AB为直径的⊙O的位置关系是( )
A.圆上 B.圆内 C.圆外 D.不能确定
3.如图,线段AB是⊙O的直径,弦CD⊥AB,BC=OD=2,DC的长等于( )
A.2 B.4 C. D.2
4.如图,在半径为5的中,弦BC,DE所对的圆心角分别是,.若,,则弦BC的弦心距为( ).
A. B. C.4 D.3
5.如图,点I为的内心,连接并延长交的外接圆于点D,点E为弦的中点,连接,,,当,,时,的长为( )
A.5 B.4.5 C.4 D.3.5
6.如图,在Rt△ABC中,∠C=90°,AC=5,⊙O是△ABC的内切圆,半径为2,则图中阴影部分的面积为( )
A.30﹣4π B. C.60﹣16π D.
7.如图,已知AB为⊙O的弦,C为的中点,点D在优弧上一点,连接AD下列式子一定正确的是( )
A.∠ADC=∠B B.∠ADC+2∠B=90°
C.2∠ADC+∠B=90° D.∠B=30°
8.如图,扇形OBA中,点C在弧AB上,连接BC,P为BC中点.若,,则点C沿弧从点B运动到点A的过程中,点P所经过的路径长为( )
A. B. C. D.6
9.如图,将两个正方形如图放置(B,C,E共线,D,C,G共线),若AB=3,EF=2,点O在线段BC上,以OF为半径作⊙O,点A,点F都在⊙O上,则OD的长是( )
A.4 B. C. D.
10.如图,C为半圆内一点,O为圆心,直径长为,,将绕圆心O逆时针旋转至,点在上,则边扫过区域(图中阴影部分)的面积为( )
A. B. C. D.
二、填空题
11.如图,的半径为13,,分别以点A,B为圆心,大于的长为半径作弧,两弧相交于点M,N,作直线交于点C,则________.
12.已知的半径为5,为圆内的一点,,则过点P的弦长的最小值是________.
13.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是_______.
14.如图,在菱形ABCD中,,,点E是射线CD上一点,连接BE,点P在BE上,连接AP,若,则面积的最大值为__________.
15.如图,平面直角坐标系xOy中,点A的坐标为(4,),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若,则点P的坐标为________.
16.在正六边形ABCDEF中,对角线AC,BD相交于点M,则的值为______.
17.如图,正六边形ABCDEF的边长为4,以A为圆心,AC的长为半径画弧,得,连接AC、AE,用图中阴影部分作一个圆锥的侧面,则这个圆锥的底面半径为______.
18.已知,OA是⊙O的半径,延长AO至点B,使得OB=3OA=3,以B为直角顶点,做等腰直角△BMC,且满足点M始终在⊙O上(如图所示),连接OC,则OC的最大值为______.
三、解答题
19.与圆相关的定理,我们在初中阶段已经学习了很多.例如:垂径定理、圆周角定理和切线长定理等.实际上,与圆相关的定理还有很多,比如下面的定理:若内接于圆的四边形的对角线互相垂直,则圆心到一边的距离等于这条边所对的边的一半,如下给出了不完整的“已知”,请补充完整,并证明.
已知:四边形是的内接四边形,________,过点O作于点E.求证:.
20.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
21.已知是的直径,弦与相交,.
(Ⅰ)如图①,若为的中点,求和的大小;
(Ⅱ)如图②,过点作的切线,与的延长线交于点,若,求的大小.
22.如图,AB是⊙O的直径,点C是⊙O上的一点,OD⊥AB交AC于点E,∠D=2∠A.
(1) 求证:CD是⊙O的切线;
(2) 求证:DE=DC;
(3) 若OD=5,CD=3,求AE的长.
23.如图,正方形的边长为4,以为直径在正方形内部作半圆O,点E在边上,,连接,和.
(1) 求证:是半圆O的切线;
(2) 请直接写出图中阴影部分的面积(用含π的代数式表示).
24.阅读与思考:阿基米德(公元前287年-公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家、静态力学和流体静力学的奠基人,并且享有“力学之父”的美称,留给后人的最有价值的书是《阿基米德全集》.在该书的“引理集”中有这样一道题:
如图1,以为直径作半圆O,弦是一个内接正五边形的一条边(即:),点D是的中点,连接并延长与直径的延长线交于点E,连接交于点F,过点F作于点M.求证:是半圆的半径.
下面是勤奋小组的部分证明过程:
证明:如图2,过点D作于点H.
∵,
∴.(依据1)
∵点D是的中点,
∴.
∵,
∴.
∴.(依据2)
∵以为直径作半圆O,
∴.(依据3)
∴.
∵四边形是半圆O的内接四边形,
∴.(依据4)
∵,
∴.
∵于点M,
∴.
∵,
∴.
∵.
∵.
∴.
∴.
……
通过上面的阅读,完成下列任务:
(1)任务一:直接写出依据1,依据2,依据3和依据4;
(2)任务二:根据勤奋小组的解答过程完成该题的证明过程.(提示:先求出的度数,再根据等腰三角形的性质或判定完成该题的证明过程)
答案
一、单选题
1.C
【分析】根据弧、弦的概念、对称轴的概念、过三点的圆的条件判断即可.
解:A、弦不一定是直径,但直径是弦,本选项说法错误,不符合题意;
B、半圆小于优弧,半圆是圆中最长的弧说法错误,本选项不符合题意;
C、圆的每一条直径所在的直线都是它的对称轴,本选项说法正确,符合题意;
D、过不在同一直线上的三点可以作一个圆,本选项说法错误,不符合题意;
故选:C.
2.A
【分析】根据题意可知,的中点为点,连接,先根据等边三角形的性质可得,再根据三角形中位线定理可得,从而可得为的半径,由此即可得.
解:如图,由题意可知,的中点为点,连接,
是等边三角形,
,
是的中点,为的中点,
,
,
即为的半径,
点在上,
故选:A.
3.D
【分析】如图,令、的交点为,由垂径定理得,证明,则,,在中,由勾股定理得,求出的值,根据计算求解的值即可.
解:如图,令、的交点为,
∵,是的直径,
∴,
在和中,
∵,
∴,
∴,
∴,
在中,由勾股定理得,
∴,
故选D.
4.D
【分析】作AH⊥BC于H,作直径CF,连接BF,先利用等角的补角相等得到∠DAE=∠BAF,再利用圆心角、弧、弦的关系得到DE=BF=6,由AH⊥BC,根据垂径定理得CH=BH,则AH为△CBF的中位线,然后根据三角形中位线性质得到AH=BF=3.
解:作AH⊥BC于H,作直径CF,连接BF,如图,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴,
∴DE=BF=6,
∵AH⊥BC,
∴CH=BH,
而CA=AF,
∴AH为△CBF的中位线,
∴AH=BF=3,
故选:D.
5.C
【分析】延长ID到M,使DM=ID,连接CM.想办法求出CM,证明IE是△ACM的中位线即可解决问题.
解:延长ID到M,使DM=ID,连接CM.
∵I是△ABC的内心,
∴∠IAC=∠IAB,∠ICA=∠ICB,
∵∠DIC=∠IAC+∠ICA,∠DCI=∠BCD+∠ICB,
∴∠DIC=∠DCI,
∴DI=DC=DM,
∴∠ICM=90°,
∴CM==8,
∵AI=2CD=10,
∴AI=IM,
∵AE=EC,
∴IE是△ACM的中位线,
∴IE=CM=4,
故选:C.
6.A
【分析】先由切线长定理和勾股定理算出三角形另外两边的长,再根据图中阴影部分的面积=△ABC的面积-⊙O的面积,然后利用三角形的面积公式和圆的面积公式计算即可.
解:过点O作AB、AC、BC的垂线,垂足分别为D、E、F,如图,
,
∴四边形CEOF是矩形,
,
∴四边形CEOF是正方形,
,
∵⊙O是△ABC的内切圆,
,
设,
在中,,
,
解得,
,
.
故选A.
7.C
【分析】先利用垂径定理,由C为的中点得到OC⊥AB,则∠A+∠AOC=90°,然后根据圆周角定理得到∠AOC=2∠ADC,加上∠A=∠B,于是可判断C选项一定正确.
解:∵C为的中点,
∴OC⊥AB,
∴∠A+∠AOC=90°,
∵∠AOC=2∠ADC,
∴2∠ADC+∠A=90°,
∵OA=OB,
∴∠A=∠B,
∴∠2ADC+∠B=90°.
故选:C.
8.B
【分析】连接OC、OP,易得∠OPB=90°,点P是在以OB的中点D为圆心,BD为半径的圆上运动,求即可.
解:连接OC、OP,
∵OB=OC,
∴△BOC为等腰三角形,
∵P为BC中点,
∴OP⊥BC(三线合一),
即∠OPB=90°,
∴点P是在以OB的中点D为圆心,BD为半径的圆上运动,如图所示,
当点C运动到点A时,点P到达位置,
点P所经过的路径长为,
连接,∵D为OB中点,为AB中点,
∴∥OA,
∴=,BD=OA=3,
∴,
即点P所经过的路径长为 ,
故选:B.
9.B
【分析】连接OA,OF,由题意得OA=OF,设OC=x,由勾股定理得,解答方程可得OC的值,再运用勾股定理可得OD的长.
解:连接OA,OF,如图,
∵OF是半圆O的半径,
∴OA=OF,
∵四边形ABCD、EFGC是正方形,
∴,
设,
∴BO=BC-OC=3-x,OE=OC+CE=x+2,
在Rt和Rt中,
,
∴,
∵
∴,
解得,,即OC=1,
在Rt中,,
∴,
故选:B.
10.B
【分析】根据已知条件和旋转的性质得出两个扇形的圆心角的度数,再根据扇形的面积公式进行计算即可得出答案.
解:∵∠BOC=60°,△B′OC′是△BOC绕圆心O逆时针旋转得到的,
∴∠B′OC′=60°,△BCO=△B′C′O,
∴∠B′OC=60°,∠C′B′O=30°,
∴∠B′OB=120°,
∵AB=2cm,
∴OB=1cm,OC′=cm,
∴B′C′=cm,
∴S扇形B′OB= cm2,
S扇形C′OC= cm2,
∴阴影部分面积=S扇形B′OB+S△B′C′O-S△BCO-S扇形C′OC=S扇形B′OB-S扇形C′OC=cm2;
故选:B.
二、填空题
11.12
【分析】连接OC、OB,根据作图可知OC是线段AB的垂直平分线,则有BC=AC=AB.在Rt△BOC中,利用勾股定理即可求解OC.
解:连接OC、OB,如图,
根据作图可知,OC是线段AB的垂直平分线,
则有BC=AC=AB=10×=5,
又∵圆的半径OB=13,
∴在Rt△BOC中,利用勾股定理可得:,
故答案为:12.
12.8
【分析】过P点作弦AB,使AB⊥OP,则AB为过P点的最短的弦,连结OA,根据垂径定理得AP=BP,在Rt△AOP中,根据勾股定理可计算出AP=4,则AB=2AP=8.
解:过P点作弦AB,使AB⊥OP,则AB为过P点的最短的弦,
连结OA,
∵OP⊥AB,
∴AP=BP,
在Rt△AOP中,OA=5,OP=3,
∴AP=,
∴AB=2AP=8.
故答案为:8.
13.
【分析】连接OD,交AC于F,根据垂径定理的推论得出OD⊥AC,AF=CF,进而证得DF=BC,根据三角形中位线定理求得OF=BC=DF,从而求得BC=DF,利用勾股定理即可求得AC.
解:如图,连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中,
,
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,AB=2OD=6,
∴BC=2,
∴.
故答案为:.
14.
【分析】若要使的面积最大,底AB固定,故只要AB边上的高最大时,即三角形面积最大;可证,故可知点P在△APB的外接圆的劣弧上,当点P在劣弧的中点处,△APB的面积最大,求出AB边上的高即可求解.
解:∵四边形ABCD是菱形,
∴AB=BC=6,AB//CD,
∴
∵,
∴ 即,
∵,
∴,
∵,
∴点P在在△APB的外接圆上,
若要使的面积最大,底AB固定,,故只要AB边上的高最大时,即三角形面积最大;此时点P在劣弧的中点处,如图,
设点O为△APB的外接圆的圆心,OP⊥AB于点F,
∴,,
∴
∴
由勾股定理得,
∴
∴PF=
∴
即面积的最大值为.
故答案为:.
15.(0,)
【分析】连接AB,过点A分别作AC⊥x轴、AD⊥y轴,利用根据圆的切线性质可知△PAB、△AOC为直角三角形,AB=AC=,利用直角三角形中30°角的性质和勾股定理分别求出AP、AD的长度,进而求出OD、PD的长度即可求得答案.
解:如图,过点A分别作AC⊥x轴于点C、AD⊥y轴于点D,连接AB,
∵AD⊥y轴,AC⊥x轴,
∴四边形ADOC为矩形.
∴AC=OD,OC=AD.
∵⊙A与x轴相切,
∴AC为⊙A的半径.
∵点A坐标为(4,),
∴AC=OD=,OC=AD=4,
∵PB是切线,
∴AB⊥PB.
∵∠APB=30°,
∴PA=2AB=5.
在Rt△PAD中,根据勾股定理,得,
∴OP=PD+DO=.
∵点P在y轴的正半轴上,
∴点P坐标为(0,).
故答案为:(0,).
16.2
【分析】根据多边形的内角和公式即可得出∠ABC,∠BCD的度数,再根据等腰三角形的性质证明,设 则则 从而可得答案.
解:∵六边形ABCDEF是正六边形,
∴∠BCD=∠ABC= (6-2)×180°=120°,AB=BC=CD,
∴∠BAC=∠ACB=∠CBD=∠CDB=(180°-120°)=30°,
∠ABM =90°,
设 则
故答案为2.
17.
【分析】由正六边形ABCDEF的边长为4,可得AB=BC=4,∠ABC=∠BAF=120°,进而求出∠BAC=30°,∠CAE=60°,过B作BHAC于H,由等腰三角形的性质和含30°直角三角形的性质得到AH=CH=AC,BH=2.在RtABH中,由勾股定理求得AH=,得到.根据扇形的面积公式可得到阴影部分的面积,即是圆锥的侧面积,最后根据圆锥的侧面积公式求解底面半径即可.
解:∵正六边形ABCDEF的边长为4,
∴AB=BC=4,
,
∵∠ABC+∠BAC+∠BCA=180°,
∴,
如图,过B作BHAC于H,
∴AH=CH=AC,
,
在RtABH中,
,
∴,
同理可求∠EAF=30°,
∴,
∴,
∴,
∵,
∴,
∴r=,
故答案为:.
18.或
【分析】由“SAS”可证△NBM≌△OBC,可得MN=OC,则当点O在线段MN上时,MN有最大值,即可求解.
解:如图,过点B作BN⊥AB,且BN=OB,连接ON,OM,MN,
∴∠NBO=90°=∠MBC,
∴∠MBN=∠OBC,
在△NBM和△OBC中,
∵MB=BC,∠MBN=∠OBC,BN=OB,
∴△NBM≌△OBC(SAS),
∴MN=OC,
∵MN≤OM+ON,
∴当点O在线段MN上时,MN有最大值,
∵OB=3OA=3,
∴,
∴MN的最大值为,
∴OC的最大值为,
故答案为:
三、解答题
19.
证明:连接并延长交于点F,连接,如图所示,
∵为直径,
∴,即,
又∵,
∴,
∵,
∴,
∴是的中位线,
∴,
∵,
∴,
∴,
∴.
20.
(1)证明:如答图,过点O作OE⊥AB于点E,
∵AE=BE,CE=DE,
∴BE﹣DE=AE﹣CE,
即AC=BD
(2)由(1)可知,OE⊥AB且OE⊥CD,
连接OC,OA,
∵OA=10,OC=8,OE=6,
∴.
∴AC=AE﹣CE=8﹣.
21.
解:(Ⅰ)∵是的直径,∴.
∴.
又∴,∴.
由为的中点,得.
∴.
∴.
(Ⅱ)如图,连接.
∵切于点,
∴,即.
由,又,
∴是的外角,
∴.
∴.
又,得.
∴.
22.
(1)证明:连接OC,如图,
∵OA=OC,
∴∠ACO=∠A,
∴∠COB=∠A+∠ACO=2∠A,
又∵∠D=2∠A,
∴∠D=∠COB.
又∵OD⊥AB,
∴∠COB+∠COD=90°,
∴∠D+∠COD=90°,即∠DCO=90°,
∴OC⊥DC,
又点C在⊙O上,
∴CD是⊙O的切线;
(2)证明:∵∠DCO=90°,
∴∠DCE+∠ACO=90°,
又∵OD⊥AB,
∴∠AEO+∠A=90°,
又∵∠A=∠ACO,∠DEC=∠AEO,
∴∠DEC=∠DCE,
∴DE=DC;
(3)解:∵∠DCO=90°,OD=5,DC=3,
∴OC===4,
∴OA=OC=4,
又DE=DC=3,
∴OE=OD﹣DE=2,
在Rt△AEO中,由勾股定理得:,
∴AE=2.
23.
(1)解:过点O作OF⊥DE于F,如图所示:
在中,,,CE=BC-BE=4-1=3,
,
在中,,,
,
在中,,,
,
,
三角形是直角三角形,且,
,
,
,
是圆的半径,且,
是半圆O的切线.
(2).
24.
(1)解:依据1:一条弧所对的圆周角等于它所对圆心角度数的一半(或圆周角定理);
依据2:同弧或等弧所对的圆周角相等;
依据3:直径所对的圆周角是直角;
依据4:圆内接四边形的对角互补;
(2)解:∵,
∴,
∵于点H,
∴,
∴,
∵是的外角,
∴,
∴,
∴,
∴,
∴,
∴,
∴是半圆的半径.
同课章节目录
