浙教版数学八年级下册5.1 矩形(第二课时) 教案(表格式)
文档属性
| 名称 | 浙教版数学八年级下册5.1 矩形(第二课时) 教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 173.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-07 00:00:00 | ||
图片预览

文档简介
教学设计
课程基本信息
学科 数学 年级 八年级 学期 春季
课题 矩形(第二课时)
教学目标
1.理解并掌握矩形的判定方法。 2.使学生能应用矩形的定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力。 3.在矩形判定定理的理解过程中,感悟数学推理,培养学生数学几何推理的表达能力。
教学内容
教学重点: 矩形的判定 教学难点: 矩形判定定理的证明以及灵活应用
教学过程
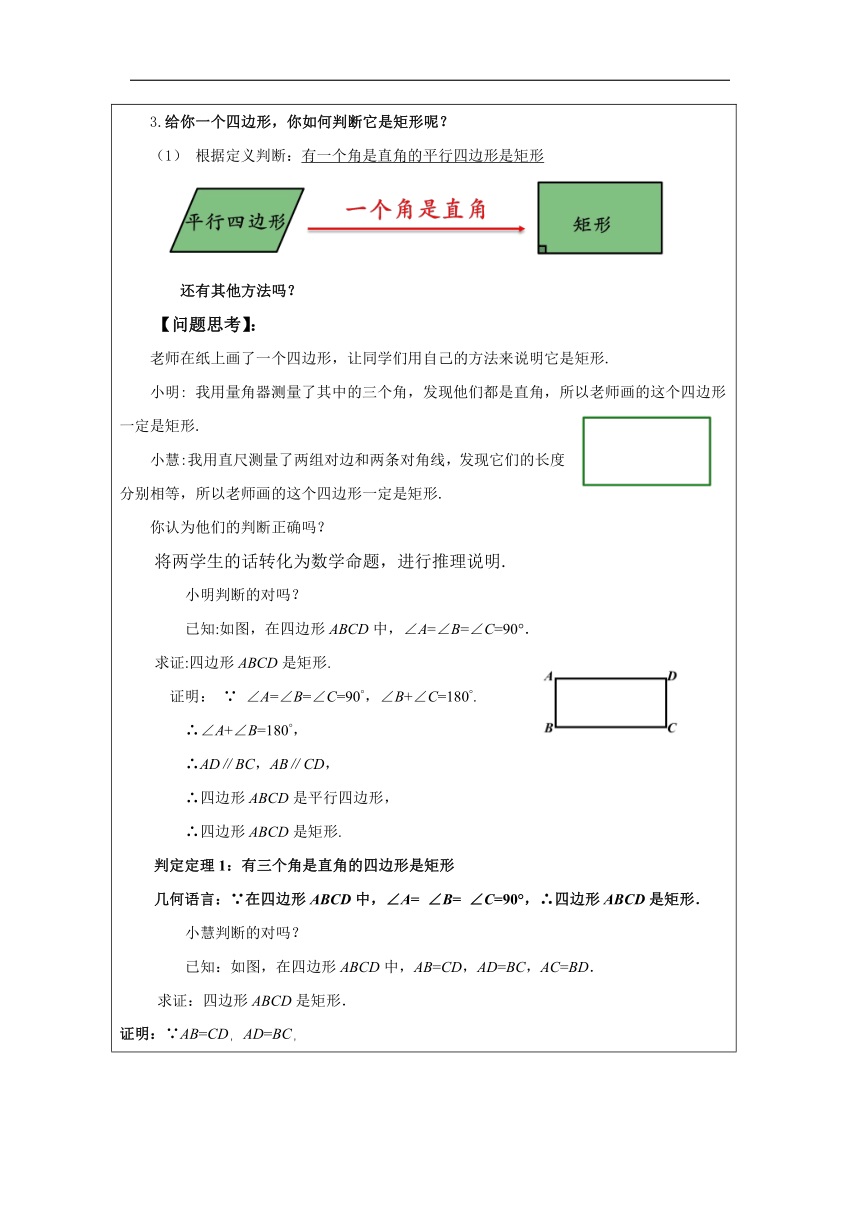
一、问题引导、引发思考 同学们,在上一节课中,我们学习了矩形的定义和性质,请类比平行四边形的研究历程,你觉得我们接下来研究什么呢? 【复习回顾】: 1.具有平行四边形的所有性质: 对边平行且相等;对角相等、邻角互补;对角线互相平分 2.矩形的特殊性质:四个角都是直角;对角线相等 3.给你一个四边形,你如何判断它是矩形呢? (1) 根据定义判断:有一个角是直角的平行四边形是矩形 还有其他方法吗? 【问题思考】: 老师在纸上画了一个四边形,让同学们用自己的方法来说明它是矩形. 小明: 我用量角器测量了其中的三个角,发现他们都是直角,所以老师画的这个四边形一定是矩形. 小慧:我用直尺测量了两组对边和两条对角线,发现它们的长度分别相等,所以老师画的这个四边形一定是矩形. 你认为他们的判断正确吗? 将两学生的话转化为数学命题,进行推理说明. 小明判断的对吗? 已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明: ∵ ∠A=∠B=∠C=90°,∠B+∠C=180°. ∴∠A+∠B=180°, ∴AD∥BC,AB∥CD, ∴四边形ABCD是平行四边形, ∴四边形ABCD是矩形. 判定定理1:有三个角是直角的四边形是矩形 几何语言:∵在四边形ABCD中,∠A= ∠B= ∠C=90°,∴四边形ABCD是矩形. 小慧判断的对吗? 已知:如图,在四边形ABCD中,AB=CD,AD=BC,AC=BD. 求证:四边形ABCD是矩形.
证明:∵AB=CD,AD=BC, ∴四边形ABCD是平行四边形. 又∵AC=BD,AD=BCDC=CD, ∴△ADC≌△BCD(SSS). ∴∠ADC=∠BCD, 又∵AD∥BC, ∴∠ADC=∠BCD=90°, ∴四边形ABCD是矩形. 判定定理2:对角线相等的平行四边形是矩形. 几何语言:∵在□ABCD中,AC=BD,∴□ABCD是矩形. 二、典例分析、深化认知 例:如图,一张四边形纸板ABCD的两条对角线互相垂直.若要从这张纸板中剪出一个矩形,并使它的四个顶点分别落在四边形ABCD的四条边上,可怎样剪? 解:如图,分别取AB,BC,CD,DA的中 点E,F,G,H,依次连结EF,FG,GH,HE.沿四边形EFGH的各条边剪,就能剪出符合要求的矩形. 下面给出证明. 解 :∵EF是△ABC的一条中位线, ∴EF//AC. ∵AC⊥BD,∴EF⊥BD. ∵EH是△ABD的一条中位线, ∴EH∥BD, ∴EF⊥EH,即∠HEF=Rt∠. 同理,∠EHG=Rt∠,∠HGF=Rt∠. ∴四边形EFGH是矩形(有三个角是直角的四边形是矩形). 三、同步练习、巩固新知 1.判断下列命题是否正确,并说明理由. (1)对角互补的平行四边形是矩形.正确 (2)一组邻角相等的平行四边形是矩形.正确
(3)对角线相等的四边形是矩形.错误 (4)内角都相等的四边形是矩形.正确 2.如图,BC是等腰三角形BED的底边ED上的高线,四边形ABEC是平行四边形. 求证:四边形ABCD是矩形. 证明:∵四边形ABEC是平行四边形, ∴AB∥CE, AB=CE, AC=BE ∵BC是等腰△BED底边ED上的高, ∴EC=CD, BE=BD, ∴AB∥CD,AB=CD ∴四边形ABCD是平行四边形. ∵AC=BE,BE=BD, ∴BD=AC, ∴平行四边形ABCD是矩形. 四、知识梳理,构建体系
课程基本信息
学科 数学 年级 八年级 学期 春季
课题 矩形(第二课时)
教学目标
1.理解并掌握矩形的判定方法。 2.使学生能应用矩形的定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力。 3.在矩形判定定理的理解过程中,感悟数学推理,培养学生数学几何推理的表达能力。
教学内容
教学重点: 矩形的判定 教学难点: 矩形判定定理的证明以及灵活应用
教学过程
一、问题引导、引发思考 同学们,在上一节课中,我们学习了矩形的定义和性质,请类比平行四边形的研究历程,你觉得我们接下来研究什么呢? 【复习回顾】: 1.具有平行四边形的所有性质: 对边平行且相等;对角相等、邻角互补;对角线互相平分 2.矩形的特殊性质:四个角都是直角;对角线相等 3.给你一个四边形,你如何判断它是矩形呢? (1) 根据定义判断:有一个角是直角的平行四边形是矩形 还有其他方法吗? 【问题思考】: 老师在纸上画了一个四边形,让同学们用自己的方法来说明它是矩形. 小明: 我用量角器测量了其中的三个角,发现他们都是直角,所以老师画的这个四边形一定是矩形. 小慧:我用直尺测量了两组对边和两条对角线,发现它们的长度分别相等,所以老师画的这个四边形一定是矩形. 你认为他们的判断正确吗? 将两学生的话转化为数学命题,进行推理说明. 小明判断的对吗? 已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明: ∵ ∠A=∠B=∠C=90°,∠B+∠C=180°. ∴∠A+∠B=180°, ∴AD∥BC,AB∥CD, ∴四边形ABCD是平行四边形, ∴四边形ABCD是矩形. 判定定理1:有三个角是直角的四边形是矩形 几何语言:∵在四边形ABCD中,∠A= ∠B= ∠C=90°,∴四边形ABCD是矩形. 小慧判断的对吗? 已知:如图,在四边形ABCD中,AB=CD,AD=BC,AC=BD. 求证:四边形ABCD是矩形.
证明:∵AB=CD,AD=BC, ∴四边形ABCD是平行四边形. 又∵AC=BD,AD=BCDC=CD, ∴△ADC≌△BCD(SSS). ∴∠ADC=∠BCD, 又∵AD∥BC, ∴∠ADC=∠BCD=90°, ∴四边形ABCD是矩形. 判定定理2:对角线相等的平行四边形是矩形. 几何语言:∵在□ABCD中,AC=BD,∴□ABCD是矩形. 二、典例分析、深化认知 例:如图,一张四边形纸板ABCD的两条对角线互相垂直.若要从这张纸板中剪出一个矩形,并使它的四个顶点分别落在四边形ABCD的四条边上,可怎样剪? 解:如图,分别取AB,BC,CD,DA的中 点E,F,G,H,依次连结EF,FG,GH,HE.沿四边形EFGH的各条边剪,就能剪出符合要求的矩形. 下面给出证明. 解 :∵EF是△ABC的一条中位线, ∴EF//AC. ∵AC⊥BD,∴EF⊥BD. ∵EH是△ABD的一条中位线, ∴EH∥BD, ∴EF⊥EH,即∠HEF=Rt∠. 同理,∠EHG=Rt∠,∠HGF=Rt∠. ∴四边形EFGH是矩形(有三个角是直角的四边形是矩形). 三、同步练习、巩固新知 1.判断下列命题是否正确,并说明理由. (1)对角互补的平行四边形是矩形.正确 (2)一组邻角相等的平行四边形是矩形.正确
(3)对角线相等的四边形是矩形.错误 (4)内角都相等的四边形是矩形.正确 2.如图,BC是等腰三角形BED的底边ED上的高线,四边形ABEC是平行四边形. 求证:四边形ABCD是矩形. 证明:∵四边形ABEC是平行四边形, ∴AB∥CE, AB=CE, AC=BE ∵BC是等腰△BED底边ED上的高, ∴EC=CD, BE=BD, ∴AB∥CD,AB=CD ∴四边形ABCD是平行四边形. ∵AC=BE,BE=BD, ∴BD=AC, ∴平行四边形ABCD是矩形. 四、知识梳理,构建体系
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
