3.7 正多边形
图片预览






文档简介
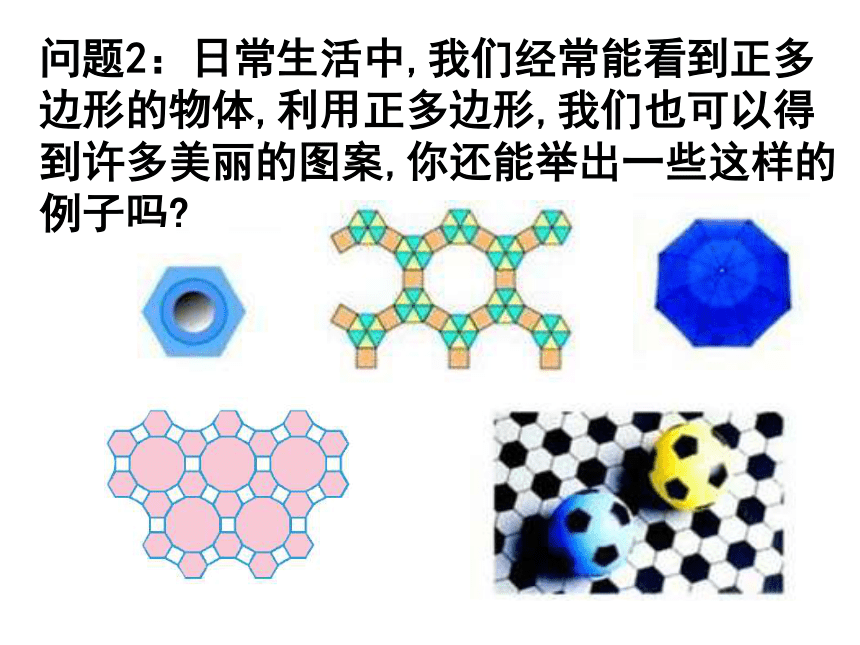
课件24张PPT。 这个美丽图案的主体部分由一些多边形构成.你发现这些多边形有什么特别之处吗?3.7 正多边形问题1:什么样的图形是正多边形?定义:各边相等,各角也相等的多边形是正多边形.根据正多边形的边数的不同,分别把它们叫做正三角形、正方形、正五边形、正六边形等.问题2:日常生活中,我们经常能看到正多边形的物体,利用正多边形,我们也可以得到许多美丽的图案,你还能举出一些这样的例子吗?例1 已知一个正多边形的内角为176.4°,这个正多边形是几边行?有没有内角为100°的正多边形?
1.如果正多边形的一个外角等于45°,那么它的边数为 ( )
A.6 B.7
C.8 D.9【练一练】A.正十二边形 B.正十边形
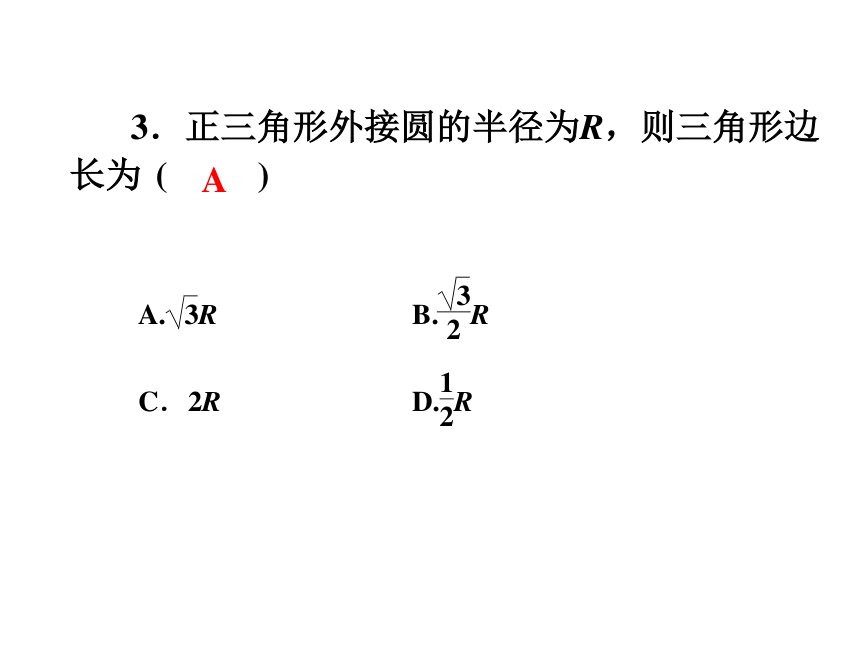
?C.正八边形 D.正六边形CB ( ) 3.正三角形外接圆的半径为R,则三角形边长为 ( )A4.正八边形如图所示,点A,B,C是它的顶点,则∠ABC=___________.22.5°你知道正多边形与圆的关系吗?做一做:课本99页探索:1.如图,已知正三角形,用直尺和圆规作它的外接圆.
2.如图,已知正方形,用直尺和圆规作它的外接圆.正多边形的外接圆 我们把经过一个正多边形的各个顶点的圆叫做这个正多边形的外接圆,这个正多边形叫做圆内接正多边形.探索: 任何正多边形都有一个外接圆. 正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.探索: 如图, 把⊙O分成相等的5段弧,依次连接各分点得到五边形ABCDE.∴ AB=BC=CD=DE=EA,∴ ∠A=∠B.同理∠B = ∠C = ∠D = ∠E.又五边形ABCDE的顶点都在⊙O上,∴ 五边形ABCDE是⊙O的内接正五边形, ⊙O是五边形ABCDE的外接圆.我们以圆内接正五边形为例证明.∵弧AB=弧BC=弧CD=弧DE=弧EA,∵弧BCE=弧CDA,正多边形每一边所对的圆心角叫做正多边形的中心角.我们把一个正多边形外接圆的圆心叫做这个正多边形的中心.外接圆的半径叫做正多边形的半径.中心到正多边形的距离叫做正多边形的边心距.第一种方法:如图,以2cm为半径作一个⊙O,用量角器画一个等于 的圆心角,它对着一段弧,然后在圆上依次截取与这条弧相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出正六边形.·O利用这种方法可以画出任意的正n边形.怎样画一个边长为2cm的正六边形?第二种方法:
如图,以2cm为半径作一个⊙O,由于正六边形的半径等于边长,所以在圆上依次截取等于2cm的弦,就可以将圆六等分,顺次连接各分点即可.·O例 有一个亭子,它的地基是半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).因此,亭子地基的周长l =4×6=24(m).利用勾股定理,可得边心距亭子地基的面积OABCDEFRPr生活中数学:练习1. 矩形是正多边形吗?菱形呢?正方形呢?为什么?矩形不一定是正多边形.因为四条边不一定都相等;菱形不一定是正多边形.因为四个角不一定都相等;正方形是正多边形.因为四条边都相等,四个角都相等.2.分别求出半径为R的圆内接正三角形,正方形的边长,边心距和面积.解:作等边△ABC的边BC上的高AD,垂足为D.连接OB,则OB=R.在Rt△OBD中 , ∠OBD=30°,边心距=OD=在Rt△ABD中 , ∠BAD=30°,·ABCDO由勾股定理,求得AB=解:连接OB,OC,过点O 作OE⊥BC垂足为E.
则∠OEB=90°,∠OBE= ∠ BOE=45°.Rt△OBE为等腰直角三角形.则有·ABCDOE几个正多边形的边长与半径的关系:a3=a4=a6=R探究活动我们来探索正多边形的轴对称性和中心对称性。1.正三角形和正方形都是轴对称图形吗?
都是中心对称图形吗?2.填写下表:3.用命题的形式概括正n边形的中心对称性和轴对称性,以及轴对称图形的对称轴的条数.1.正多边形的定义.课堂小结:这节课你学习了什么?有什么体会?2.正多边形的判定.3.正多边形的画法.4.正多边形的有关计算.1.作业本.作业:2.选做练习.
1.如果正多边形的一个外角等于45°,那么它的边数为 ( )
A.6 B.7
C.8 D.9【练一练】A.正十二边形 B.正十边形
?C.正八边形 D.正六边形CB ( ) 3.正三角形外接圆的半径为R,则三角形边长为 ( )A4.正八边形如图所示,点A,B,C是它的顶点,则∠ABC=___________.22.5°你知道正多边形与圆的关系吗?做一做:课本99页探索:1.如图,已知正三角形,用直尺和圆规作它的外接圆.
2.如图,已知正方形,用直尺和圆规作它的外接圆.正多边形的外接圆 我们把经过一个正多边形的各个顶点的圆叫做这个正多边形的外接圆,这个正多边形叫做圆内接正多边形.探索: 任何正多边形都有一个外接圆. 正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.探索: 如图, 把⊙O分成相等的5段弧,依次连接各分点得到五边形ABCDE.∴ AB=BC=CD=DE=EA,∴ ∠A=∠B.同理∠B = ∠C = ∠D = ∠E.又五边形ABCDE的顶点都在⊙O上,∴ 五边形ABCDE是⊙O的内接正五边形, ⊙O是五边形ABCDE的外接圆.我们以圆内接正五边形为例证明.∵弧AB=弧BC=弧CD=弧DE=弧EA,∵弧BCE=弧CDA,正多边形每一边所对的圆心角叫做正多边形的中心角.我们把一个正多边形外接圆的圆心叫做这个正多边形的中心.外接圆的半径叫做正多边形的半径.中心到正多边形的距离叫做正多边形的边心距.第一种方法:如图,以2cm为半径作一个⊙O,用量角器画一个等于 的圆心角,它对着一段弧,然后在圆上依次截取与这条弧相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出正六边形.·O利用这种方法可以画出任意的正n边形.怎样画一个边长为2cm的正六边形?第二种方法:
如图,以2cm为半径作一个⊙O,由于正六边形的半径等于边长,所以在圆上依次截取等于2cm的弦,就可以将圆六等分,顺次连接各分点即可.·O例 有一个亭子,它的地基是半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).因此,亭子地基的周长l =4×6=24(m).利用勾股定理,可得边心距亭子地基的面积OABCDEFRPr生活中数学:练习1. 矩形是正多边形吗?菱形呢?正方形呢?为什么?矩形不一定是正多边形.因为四条边不一定都相等;菱形不一定是正多边形.因为四个角不一定都相等;正方形是正多边形.因为四条边都相等,四个角都相等.2.分别求出半径为R的圆内接正三角形,正方形的边长,边心距和面积.解:作等边△ABC的边BC上的高AD,垂足为D.连接OB,则OB=R.在Rt△OBD中 , ∠OBD=30°,边心距=OD=在Rt△ABD中 , ∠BAD=30°,·ABCDO由勾股定理,求得AB=解:连接OB,OC,过点O 作OE⊥BC垂足为E.
则∠OEB=90°,∠OBE= ∠ BOE=45°.Rt△OBE为等腰直角三角形.则有·ABCDOE几个正多边形的边长与半径的关系:a3=a4=a6=R探究活动我们来探索正多边形的轴对称性和中心对称性。1.正三角形和正方形都是轴对称图形吗?
都是中心对称图形吗?2.填写下表:3.用命题的形式概括正n边形的中心对称性和轴对称性,以及轴对称图形的对称轴的条数.1.正多边形的定义.课堂小结:这节课你学习了什么?有什么体会?2.正多边形的判定.3.正多边形的画法.4.正多边形的有关计算.1.作业本.作业:2.选做练习.
同课章节目录
