初中数学浙教版八年级下册 第四章 平行四边形提高训练 含解析
文档属性
| 名称 | 初中数学浙教版八年级下册 第四章 平行四边形提高训练 含解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 996.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-08 00:00:00 | ||
图片预览


文档简介
八下第四章平行四边形提高训练
一、选择题
1.下列新能源汽车标志图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.如图,足球的表面是由正五边形和正六边形拼接而成,其中黑皮的正五边形有12块,白皮的正六边形有20块.如图,足球图片中的一块黑色皮块的内角和是( )
A.180° B.360° C.540° D.720°
3.在□ABCD中,若∠A:∠B:∠C=1:2:1,则∠D的度数为( )
A.67.5° B.90° C.112.5° D.120°
4.依据所标数据,下列四边形一定为平行四边形的是( )
A. B. C. D.
5.如图,平行四边形的对角线,交于点,已知,,的周长为15,则的长为( )
A.5 B.6 C.7 D.8
6.如图,在Rt△ABC中,D为斜边AC的中点,E为BD上一点,F为CE的中点若AE=AD,DF=2,则BD的长为( )
A. B.3 C. D.4
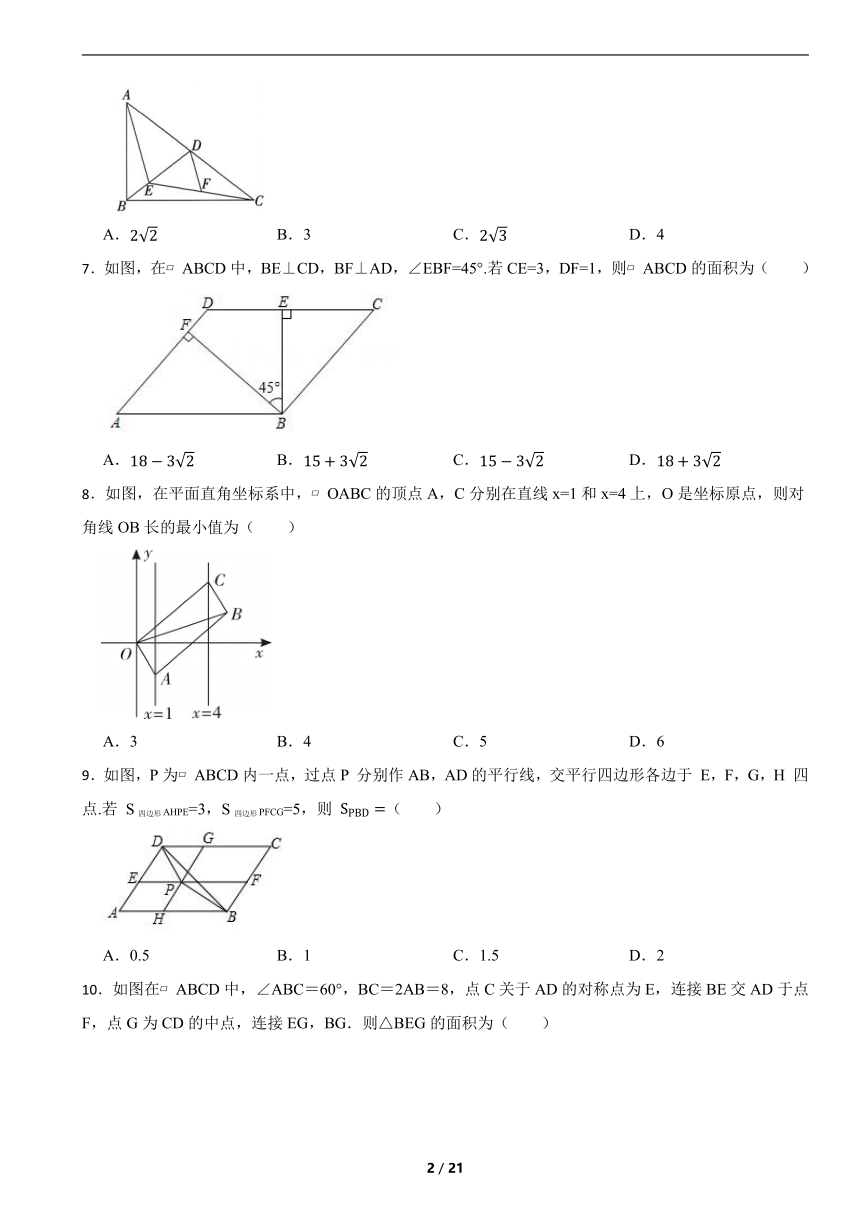
7.如图,在 ABCD中,BE⊥CD,BF⊥AD,∠EBF=45°.若CE=3,DF=1,则 ABCD的面积为( )
A. B. C. D.
8.如图,在平面直角坐标系中, OABC的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为( )
A.3 B.4 C.5 D.6
9.如图,P为 ABCD内一点,过点P 分别作AB,AD的平行线,交平行四边形各边于 E,F,G,H 四点.若 S四边形AHPE=3,S四边形PFCG=5,则 ( )
A.0.5 B.1 C.1.5 D.2
10.如图在 ABCD中,∠ABC=60°,BC=2AB=8,点C关于AD的对称点为E,连接BE交AD于点F,点G为CD的中点,连接EG,BG.则△BEG的面积为( )
A.16 B.14 C.8 D.7
二、填空题
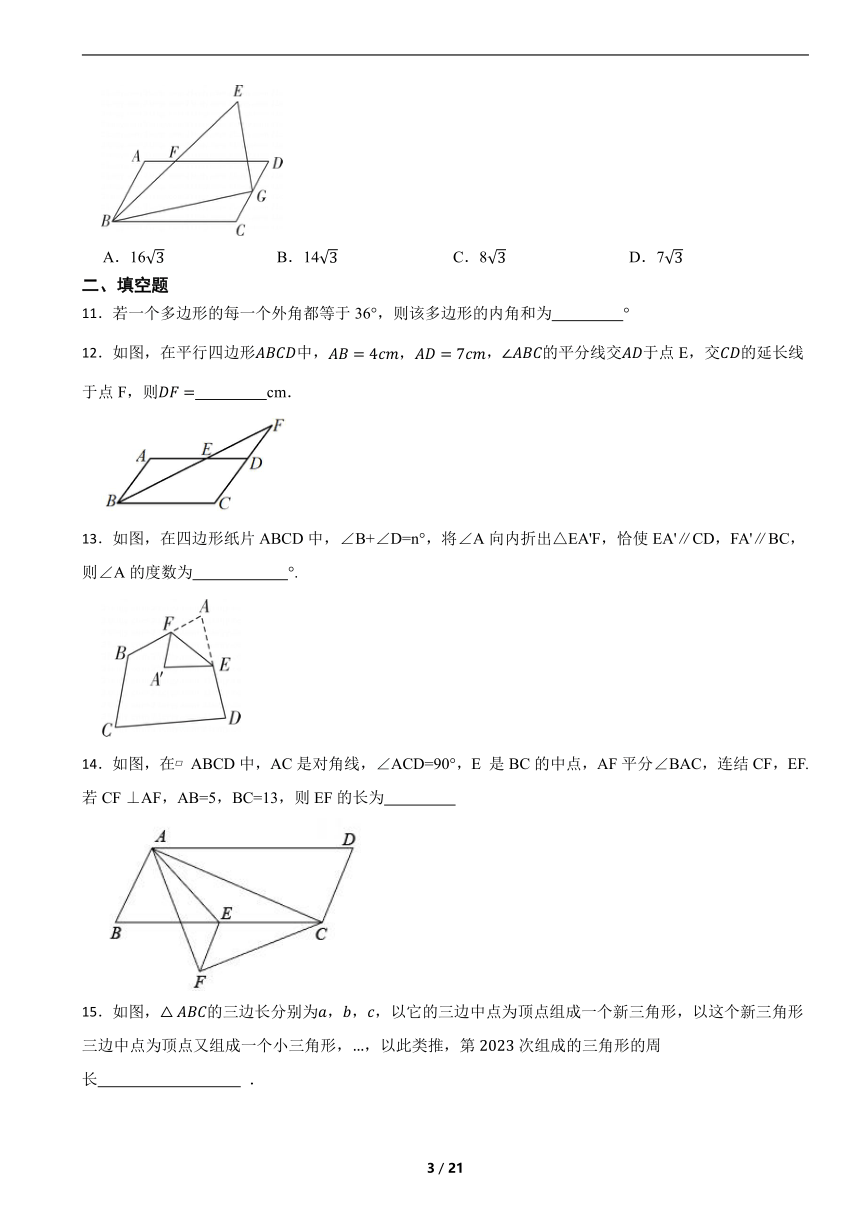
11.若一个多边形的每一个外角都等于36°,则该多边形的内角和为 °
12.如图,在平行四边形中,,的平分线交于点E,交的延长线于点F,则 cm.
13.如图,在四边形纸片ABCD中,∠B+∠D=n°,将∠A向内折出△EA'F,恰使EA'∥CD,FA'∥BC,则∠A的度数为 °.
14.如图,在 ABCD中,AC是对角线,∠ACD=90°,E 是BC的中点,AF平分∠BAC,连结CF,EF.若CF ⊥AF,AB=5,BC=13,则EF的长为
15.如图,的三边长分别为,,,以它的三边中点为顶点组成一个新三角形,以这个新三角形三边中点为顶点又组成一个小三角形,,以此类推,第次组成的三角形的周长 .
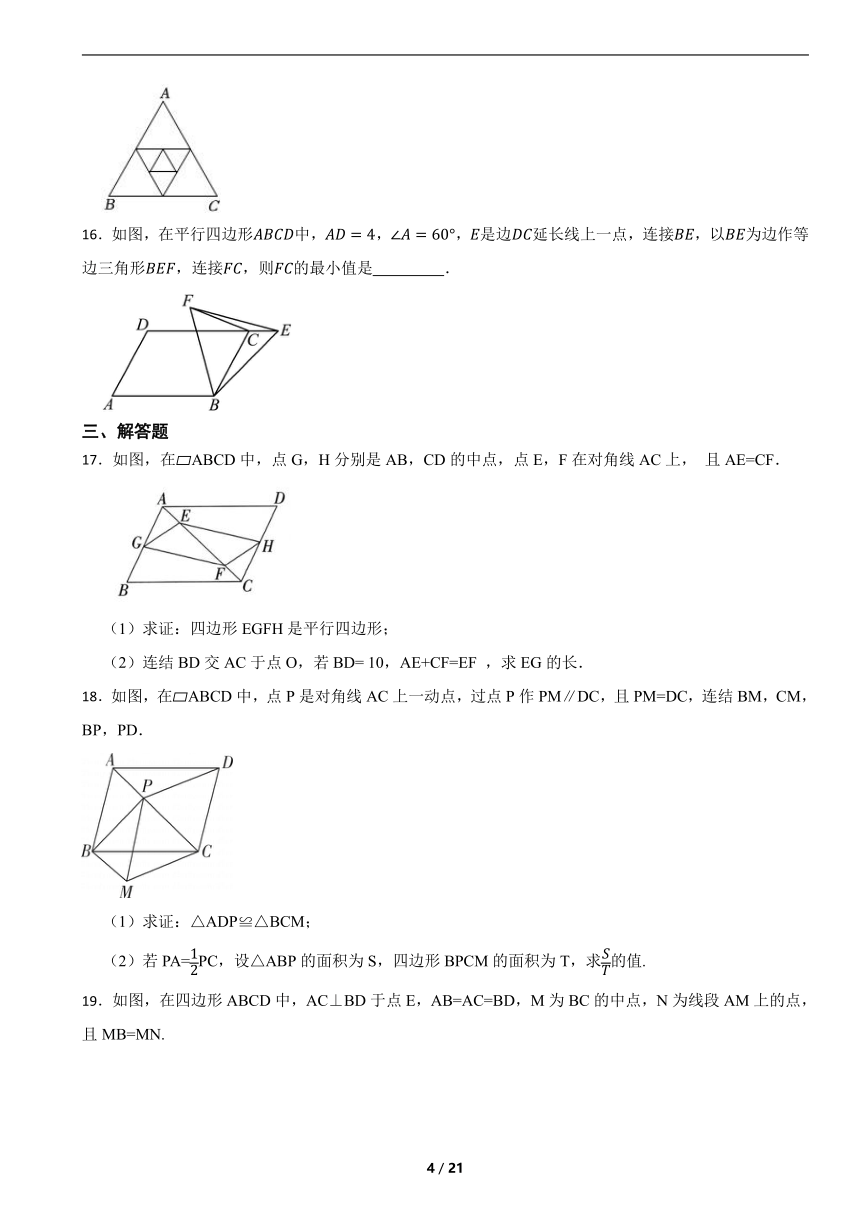
16.如图,在平行四边形中,,,是边延长线上一点,连接,以为边作等边三角形,连接,则的最小值是 .
三、解答题
17.如图,在ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上, 且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连结BD交AC于点O,若BD= 10,AE+CF=EF ,求EG的长.
18.如图,在ABCD中,点P是对角线AC上一动点,过点P作PM∥DC,且PM=DC,连结BM,CM,BP,PD.
(1)求证:△ADP≌△BCM;
(2)若PA=PC,设△ABP的面积为S,四边形BPCM的面积为T,求的值.
19.如图,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,M为BC的中点,N为线段AM上的点,且MB=MN.
(1)求证:BN平分∠ABE.
(2)连结DN,若BD=1,四边形DNBC为平行四边形,求线段BC的长.
20.在□ABCD 中,∠ABC = 45°,对角 线 AC ⊥CD.
(1)如图1,若 AD=6,求□ABCD的面积.
(2)如图2,连结 BD交 AC 于点O,过点 A 作AE⊥BD于点 E,连结 EC.求证:ED=AE+EC.
21.
(1)如图1,∠A+∠B+∠C+∠D+∠E= °.
(2)若将图1中星形的一个角截去,如图2,则∠A+∠B+∠C+∠D+∠E+∠F= °.
(3)若再将图2中图形的角截去,如图3,则由(2)中所得的方法或规律,猜想∠A+∠B+∠C+∠D+∠E+∠F+∠F+∠H+∠M+∠N= °.
22.已知,点E是的中线上一动点,交于点F,连接.
(1)如图1,当点E与点D重合时,求证:;
(2)如图2,当点E与点D不重合时,延长交于点G,交于点H.
①判断四边形的形状,并说明理由;
②如图3,若的边,以为腰作等腰直角,连接,点M为的中点,当点E从点D运动到点A过程中,请直接写出点M的运动路径长.
答案解析部分
1.【答案】A
【解析】【解答】解:A、 既是轴对称图形,又是中心对称图形,故符合题意;
B、是轴对称图形,但不是中心对称图形,故不符合题意;
C、既不是轴对称图形,也不是中心对称图形,故不符合题意;
D、是轴对称图形,但不是中心对称图形,故不符合题意;
故答案为:A.
【分析】中心对称图形:把一个图形绕着某一点旋转180°后,旋转后的图形能够与原来的图形重合,轴对称图形:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形,据此逐项判断即可.
2.【答案】C
【解析】【解答】解:∵黑色是正五边形,
∴一块黑色皮块的内角和为(5-2)×180°=540°.
故答案为:C.
【分析】根据内角和公式(n-2)×180°进行计算.
3.【答案】D
【解析】【解答】解: 在□ABCD中,∠A+∠B=180°,∠D=∠B,
∵∠A:∠B=1:2,
∴∠B=180°×=120°,
∴∠D=∠B=120°.
故答案为:D.
【分析】由平行四边形的性质可得∠A+∠B=180°,∠D=∠B,利用∠A:∠B=1:2求出∠B的度数即可.
4.【答案】D
【解析】【解答】A、两组对角分别相等的四边形是平行四边形,,A错误;
B、一组对边平行,另一组对边相等的四边形可能是等腰梯形,B错误;
C、一组对边相等的四边形不能判断是平行四边形,C错误;
D、一组对边平行且相等的四边形是平行四边形,D正确;
故答案为:D.
【分析】根据平行四边形的判定定理判断即可.
5.【答案】C
【解析】【解答】∵平行四边形的对角线,交于点,已知,,
∴BO=DO=BD=5,CO=AO=AC=3,
∵的周长为15,
∴BC=15-(BO+CO)=15-(5+3)=7,
∴AD=BC=7,
故答案为:C.
【分析】先利用平行四边形的性质可得BO=DO=BD=5,CO=AO=AC=3,再利用三角形的周长公式求出BC的长,最后利用平行四边形的性质可得AD=BC.
6.【答案】D
【解析】【解答】解:∵D是AC的中点,F是CE中点,DF=2,
∴AE=2DF=4,
∵AE=AD,
∴AD=4,
在Rt△ABC中,D为斜边AC的中点,
∴BD=AD=4,
故答案为:D.
【分析】根据三角形的中位线性质可知AE=2DF,从而得知AD=4,再根据直角三角形的中线性质,中线等于斜边的一半可得出答案.
7.【答案】A
【解析】【解答】解:
四边形ABCD是平行四边形
同理:
又
在中,
又
.
故答案为: A.
【分析】本题主要考查了平行四边形的性质、勾股定理.利用可推出: ,再结合可得:,进而推出:,可求出BC的长,得出AD的长,因此根据求出AF的长.利用可推出: ,再结合可得:,进而推出:,代入平行四边形的面积公式:可求出面积.
8.【答案】C
【解析】【解答】解:过点B作BD⊥直线x=4,交直线x=4于点D,作BE⊥x轴,直线x=1与OC交于点M,与x轴交于点F,直线x=4与AB交于点N,如图:
∵四边形OABC是平行四边形,
∴∠OAB=∠BCO,OC∥AB,OA=BC,
∵直线x=1与直线x=4都垂直于x轴,
∴AM∥CN,
∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,
∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC,
在△OAF和△BCD中
∴△OAF≌△BCD(ASA)
∴BD=OF=1,
∴OE=4+1=5,
∴OB=.
∵OE的值是定值,
∴当BE最小时(即B在x轴上),OB取得最小值,最小值OB=OE=5.
故答案为:C.
【分析】过点B作BD⊥直线x=4,交直线x=4于点D,作BE⊥x轴,直线x=1与OC交于点M,与x轴交于点F,直线x=4与AB交于点N,易得OB=,根据四边形OABC是平行四边形可得OA=BC,由平行线的性质可得∠OAF=∠BCD,结合已知用角边角易证△OAF≌△BCD,由OE的值是定值即可得当BE最小时(即B在x轴上),OB取得最小值,最小值OB=OE可求解.
9.【答案】B
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∵EF∥AB,GH∥AD,
∴EF∥AB∥CD,GH∥AD∥BC,
∴四边形AEPH、四边形HPFB、四边形EPGD、四边形GPFC均为平行四边形,
∴S△PDE=S△PDG=S平行四边形PEDG,S△BPH=S△BPF=S平行四边形BFPH,S△ABD=S△CBD=S平行四边形ABCD,
∵S△ABD=S△PDE+S四边形AEPH+S△BPH+S△BDP①,S△CBD=S△PDG+S四边形PGCF+S△BPF-S△BDP②,
∴①-②得S四边形AEPH-S四边形PGCF+2S△BDP=0,
又∵ S四边形AHPE=3,S四边形PFCG=5 ,
∴2S△BDP=5-3,
∴S△BDP=1.
故答案为:B.
【分析】由平行四边形的对边平行得AB∥CD,AD∥BC,由平行于同一直线的两条直线互相平行得EF∥AB∥CD,GH∥AD∥BC,根据两组对边分别平行得四边形是平行四边形得四边形AEPH、四边形HPFB、四边形EPGD、四边形GPFC均为平行四边形,由平行四边形的一条对角线平分平行四边形的面积得S△PDE=S△PDG,S△BPH=S△BPF,S△ABD=S△CBD,进而由割补法可得S△ABD=S△PDE+S四边形AEPH+S△BPH+S△BDP①,S△CBD=S△PDG+S四边形PGCF+S△BPF-S△BDP②,进而根据①-②列出方程可求解.
10.【答案】B
【解析】【解答】解:如图,取BC中点H,连接AH,连接EC交AD于点N,作EM⊥CD交CD的延长线于点M,
∵BC=2AB,BC=2BH=2CH,
∴BA=BH=CH,
又∵∠ABC=60°,
∴△ABH是等边三角形,
∴HA=HB=HC,
∴∠BAC=90°,
∴∠ACB=30°,
∵EC⊥BC,
∠BCD=180°-∠ABC=120°,
∴∠ACE=60°,∠ECM=30°,
∵BC=2AB=8,
∴CD=4,CN=EN=,
∴EC=,EM=,
∴S△BEG=S△BCE+S△ECG-S△BCG=S平行四边形ABCD,
=.
故答案为:B.
【分析】取BC中点H,连接AH,连接EC交AD于点N,作EM⊥CD交CD的延长线于点M,判断出△ABH是等边三角形,得HA=HB=HC,由等边对等角及三角形的内角和定理得∠BAC=90°,进而根据含30°角直角三角形的性质得∠ACB=30°,推出∠ACE=60°,∠ECM=30°,根据平行四边形的性质及轴对称的性质可得EC=,EM=,进而根据S△BEG=S△BCE+S△ECG-S△BCG算出答案.
11.【答案】1440
【解析】【解答】解:由题意得:,
该多边形的内角和为.
故答案为:1440.
【分析】根据多边形的外角和为360°,求出边数,再代入多边形内角和公式,即可得解.
12.【答案】3
【解析】【解答】解:∵四边形ABCD是平行四边形,AB=4cm,AD=7cm,
∴AB=CD=4cm,AB∥CD,BC=AD=7cm,
∴∠ABE=∠F,
∵BF平分∠ABC,
∴∠ABE=∠FBC,
∴∠FBC=∠F,
∴CF=BC=7cm,
∴DF=FC-CD=7-4=3cm;
故答案为:3.
【分析】由平形四边形的性质可得AB=CD=4cm,AB∥CD,BC=AD=7cm,利用平行线的性质及角平分线的定义可得∠FBC=∠F,可得CF=BC=7cm,利用DF=FC-CD即可求解.
13.【答案】
【解析】【解答】∵EA'∥CD,FA'∥BC,
∴,.
又∵∠B+∠D=n°,
∴,
又∵四边形内角和为,
∴,
∴.
故答案为:.
【分析】根据两直线平行,同位角相等,得到,,再利用四边形的内角和等于求解即可.
14.【答案】
【解析】【解答】解:延长CF和AB,交于点H,如下图:
∵四边形ABCD是平行四边形
∴AB∥CD,
∴∠ACD=∠BAC=90°
∴AC=
∵AF平分∠BAC,且CF⊥AF
∴AH=AC=12,FH=FC
∵AB=5
∴BH=12-5=7
∵点E是BC的中点,FH=FC
∴EF=BH=
故答案为:.
【分析】根据平行四边形的性质,可得∠ACD=∠BAC;根据勾股定理,可得AC的长;根据等腰三角形三线合一的性质,可得AH=HC;根据三角形中线的性质,可得EF的长.
15.【答案】
【解析】【解答】解:第1个 的周长为a+b+c
由三角形中位线定理可得:
第2个三角形的周长为(a+b+c),
第3个三角形的周长为×(a+b+c),
第4个三角形的周长为××(a+b+c),
······,
第n个三角形的周长为(a+b+c),
∴ 第次组成的三角形的周长 ;
故答案为: .
【分析】根据三角形中位线定理求解,可得规律第n个三角形的周长为(a+b+c),继而得解.
16.【答案】
【解析】【解答】解:如图,在上截取,连接并延长,作,
四边形是平行四边形,,,
,,
,
,
是等边三角形,
,,
是等边三角形,
,,
,
,
,
,
当点是边延长线上时,点在的延长线上 ,
,,
,
的最小值是,
故答案为:.
【分析】利用瓜豆原理可知点F的运动轨迹是一条直线,故勾手拉手全等三角形模型是本题的解题关键.利用等边三角形的性质通过SAS判定得到,再通过直角三角形的性质求得CM的长度即FC的最小值.
17.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠GAE=∠HCF.
∵点G,H分别是AB ,CD的中点,AB= CD,∴AG=CH.∵AE=CF,
∴△AGE≌△CHF ( SAS),∴GE= HF, ∠AEG= ∠CFH,∴∠GEF =∠HFE,∴GE∥HF.又∵GE=HF,∴四边形EGFH是平行四边形.
(2)解:连结BD交AC于点O,如图.
∵四边形ABCD是平行四边形,
∴OA = OC, OB=0D. BD= 10,
∴ OB=OD=5.∵AE= CF ,OA=OC,
∴ OE=OF.∵AE+CF= EF,
∴2AE= EF=20E,∴AE=OE.又∵点G是AB的中点,∴EG是△ABO
的中位线,∴EG=OB=2.5,∴EG的长为2.5.
【解析】【分析】(1)根据平行四边形的性质可证出△AGE≌△CHF ( SAS),再根据全等三角形的性质可得出GF=HF且GF∥HF,从而证出四边形EGFH是平行四边形;
(2)根据平行四边形的性质和已知 AE+CF=EF ,可知E是OA的中点,所以EG是△ABO的中位线,根据中位线的性质可求出EG的长度.
18.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AD= BC,∠ADC+ ∠BCD =180°.∵PM∥ DC,且PM=DC,∴四边形PMCD是平行四边形,
∴PD=CM,∠PDC+∠DCM= 180°,∴∠ADP= ∠ BCM.在△ADP和△BCM中,,∴△ADP≌△BCM( SAS). .
(2)解:如图,作BH⊥AC于点H,DG⊥AC于点G,∵四边形ABCD是平行四边形,△ABC≌△CDA,∴BH= DG,
∴,即S△BCP = 2S△ABP,,即S△ADP=S△ABP.
∵△ADP≌△BCM,∴S△ADP=S△BCM,∴
【解析】【分析】(1)根据已知条件可知四边形PMCD是平行四边形,则根据平行四边形的性质可证△ADP≌△BCM;
(2)根据四边形ABCD是平行四边形,可知△ABC≌△CDA,从而得到同底边上的高BH= DG,得到S△BCP= 2S△ABP,而△ABP和△ADP是同底等高,所以面积相等,四边形BPCM的面积=△BCP的面积+△ACM的面积,而根据(1)可知△ACM的面积=△ADP的面积,从而可得出答案.
19.【答案】(1)证明:∵AB=AC
∴∠ABC=∠ACB,
∵M是BC的中点,
∴AM⊥BC,
在Rt△ABM和Rt△CBE中,∠MAB+∠ABC=90°,∠ACB+∠EBC=90°,
∴∠MAB=∠EBC,
∵MB=MN,
∴△MBN是等腰直角三角形,
∴∠MNB=∠MBN=45°,
∵∠EBC+∠NBE=∠MAB+∠ABN=∠MNB=45°,
∴∠NBE=∠ABN,即BN平分∠ABE;
(2)解:设BM=CM=MN=a,
∵四边形DNBC是平行四边形,
∴DN=BC=2a,
在△ABN和△DBN中
∴△ABN≌△DBN(SAS)
∴AN=DN=2a,
在Rt△ABM中,由勾股定理可得AM2+BM2=AB2,
即(2a+a)2+a2=1,解得:a=,或a=-(舍去),
∴BC=2a=.
【解析】【分析】(1)由等边对等角可得∠ABC=∠ACB,根据等腰三角形的三线合一可得AM⊥BC,由同角的余角相等可得∠MAB=∠EBC,于是可得△MBN是等腰直角三角形,结合角的构成可求解;
(2)设BM=CM=MN=a,由题意用边角边可证△ABN≌△DBN,由全等三角形的性质可得AN=DN=2a,在Rt△ABM中,由勾股定理可得关于a的方程,然后由BC=2a可求解.
20.【答案】(1)解:∵AC⊥CD,
∴∠ACD=90°,
∵∠ABC=45°,平行四边形ABCD,
∴AB∥CD,
∴∠ABC=∠D=∠DAC=45°,
∴AC=CD,
∵AC2+CD2=AD2即2AC2=36,
∴AC2=18,
∴平行四边形ABCD的面积为AC2=18
(2)证明:过点C作CF⊥CE交BD于点F,
∴∠ECF=90°,
∵AE⊥BD,
∴∠ACD=∠AED=90°,
∴∠ACF+∠FCD=∠ACF+∠ACE=90°,
∴∠ACE=∠FCD,
∵平行四边形ABCD,
∴AB∥CD,
∴∠ABE=∠CDF,
∵∠ABD+∠BAE=∠BAE+∠EAC=90°,
∴∠ABE=∠EAC=∠CDF,
在△ACE和△DCF中
∴△ACE≌△DCF(SAS),
∴CE=CF,DF=AE
∴△CEF是等腰直角三角形,
∴EF2=CE2+CF2=2CE2,
∴,
∵DE=EF+DF,
∴
【解析】【分析】(1)利用垂直的定义可证得∠ACD=90°,利用平行四边形的性质及平行线的性质可证得AC=CD,利用勾股定理求出AC2的值,即可求出平行四边形ABCD的面积.
(2)过点C作CF⊥CE交BD于点F,利用垂直的定义和余角的性质可推出∠ACE=∠FCD,∠ABE=∠EAC=∠CDF,利用SAS证明△ACE≌△DCF,利用全等三角形的性质可证得CE=CF,DF=AE,可推出△CEF是等腰直角三角形,利用勾股定理可证得,然后根据DE=EF+DF,可证得结论.
21.【答案】(1)180
(2)360
(3)1080
【解析】【解答】解:(1)如图1,
∵∠1=∠2+∠D=∠B+∠E+∠D,∠A+∠C+∠1=180°,
∴ ∠A+∠B+∠C+∠D+∠E= ∠A+∠C+∠1=180°;
故答案为:180;
(2)如图2,∵∠2=∠1+∠F=∠B+∠E+∠F,∠A+∠C+∠2+∠D=360°,
∴ ∠A+∠B+∠C+∠D+∠E+∠F= ∠A+∠C+∠2+∠D=360°;
故答案为:360;
(3)由(1)(2)知:每截去一个角则增加180°,当截去5个角时,增加了180°×5的度数,
∴ ∠A+∠B+∠C+∠D+∠E+∠F+∠F+∠H+∠M+∠N=180°+180°×5=1080°.
故答案为:1080.
【分析】(1)根据三角形内角和定理和三角形外角的性质求解即可;
(2)根据三角形外角的性质和四边形内角和等于360°进行解答即可;
(3)由(1)(2)知:每截去一个角则增加180°,当截去5个角时,增加了180°×5的度数,据此即可求解.
22.【答案】(1)证明:,,
,,
为的中线,
,
在与中,
,
,
.
(2)解:①四边形是平行四边形,理由如下:
如图所示,过D作交点Q,连接.
四边形为平行四边形,
.
同(1)可证明,
,
又∵,
四边形是平行四边形;②
【解析】【解答】解:(2)②如图所示,取的中点P,连接,
∵是的中线,即点D为的中点,
∴是的中位线,
∴,
又∵,
∴由平行线的唯一性可知重合,即点E和点P重合,
∴点E为的中点,
∴,
∵四边形使平行四边形,
∴,
∴,
∴四边形是平行四边形,
∴,
∵,
∴;
∵,
∴当点E在上运动时,点F在直线上运动,
∵是等腰直角三角形,
∴,
∴点Q在直线上运动,
如图所示,以点B为原点,以为x轴,y轴建立坐标系,
设,
∴,
∴,
∴,
∴,
∵M为的中点,
∴,
∴点M在直线上运动,
当时,,当时,;
∴点M的运动轨迹是从点沿着直线运动到点,
∴点M的运动路径长为
【分析】 (1)利用ASA可证明△ACD≌△FDB,再利用全等三角形的性质可得AC=DF;
(2)①如图所示,过D作DQ∥EF交BF点Q,连接AQ,先证明四边形DEFQ为平行四边形,得到DQ=EF,同(1)可证明AC=DQ,得到AC=EF,由此即可四边形ACEF是平行四边形;
②如图所示,取CH的中点P,连接DP,利用平行四边形的性质和判定说明AE=FH,再依次说明点E在AD上运动时,点F在直线BF上运动,点Q在直线BQ上运动,点M在直线上运动,求得M点的运动轨迹为从点沿着直线运动到点,最后利用勾股定理求得点M的运动路径长.
1 / 1
一、选择题
1.下列新能源汽车标志图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.如图,足球的表面是由正五边形和正六边形拼接而成,其中黑皮的正五边形有12块,白皮的正六边形有20块.如图,足球图片中的一块黑色皮块的内角和是( )
A.180° B.360° C.540° D.720°
3.在□ABCD中,若∠A:∠B:∠C=1:2:1,则∠D的度数为( )
A.67.5° B.90° C.112.5° D.120°
4.依据所标数据,下列四边形一定为平行四边形的是( )
A. B. C. D.
5.如图,平行四边形的对角线,交于点,已知,,的周长为15,则的长为( )
A.5 B.6 C.7 D.8
6.如图,在Rt△ABC中,D为斜边AC的中点,E为BD上一点,F为CE的中点若AE=AD,DF=2,则BD的长为( )
A. B.3 C. D.4
7.如图,在 ABCD中,BE⊥CD,BF⊥AD,∠EBF=45°.若CE=3,DF=1,则 ABCD的面积为( )
A. B. C. D.
8.如图,在平面直角坐标系中, OABC的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为( )
A.3 B.4 C.5 D.6
9.如图,P为 ABCD内一点,过点P 分别作AB,AD的平行线,交平行四边形各边于 E,F,G,H 四点.若 S四边形AHPE=3,S四边形PFCG=5,则 ( )
A.0.5 B.1 C.1.5 D.2
10.如图在 ABCD中,∠ABC=60°,BC=2AB=8,点C关于AD的对称点为E,连接BE交AD于点F,点G为CD的中点,连接EG,BG.则△BEG的面积为( )
A.16 B.14 C.8 D.7
二、填空题
11.若一个多边形的每一个外角都等于36°,则该多边形的内角和为 °
12.如图,在平行四边形中,,的平分线交于点E,交的延长线于点F,则 cm.
13.如图,在四边形纸片ABCD中,∠B+∠D=n°,将∠A向内折出△EA'F,恰使EA'∥CD,FA'∥BC,则∠A的度数为 °.
14.如图,在 ABCD中,AC是对角线,∠ACD=90°,E 是BC的中点,AF平分∠BAC,连结CF,EF.若CF ⊥AF,AB=5,BC=13,则EF的长为
15.如图,的三边长分别为,,,以它的三边中点为顶点组成一个新三角形,以这个新三角形三边中点为顶点又组成一个小三角形,,以此类推,第次组成的三角形的周长 .
16.如图,在平行四边形中,,,是边延长线上一点,连接,以为边作等边三角形,连接,则的最小值是 .
三、解答题
17.如图,在ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上, 且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连结BD交AC于点O,若BD= 10,AE+CF=EF ,求EG的长.
18.如图,在ABCD中,点P是对角线AC上一动点,过点P作PM∥DC,且PM=DC,连结BM,CM,BP,PD.
(1)求证:△ADP≌△BCM;
(2)若PA=PC,设△ABP的面积为S,四边形BPCM的面积为T,求的值.
19.如图,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,M为BC的中点,N为线段AM上的点,且MB=MN.
(1)求证:BN平分∠ABE.
(2)连结DN,若BD=1,四边形DNBC为平行四边形,求线段BC的长.
20.在□ABCD 中,∠ABC = 45°,对角 线 AC ⊥CD.
(1)如图1,若 AD=6,求□ABCD的面积.
(2)如图2,连结 BD交 AC 于点O,过点 A 作AE⊥BD于点 E,连结 EC.求证:ED=AE+EC.
21.
(1)如图1,∠A+∠B+∠C+∠D+∠E= °.
(2)若将图1中星形的一个角截去,如图2,则∠A+∠B+∠C+∠D+∠E+∠F= °.
(3)若再将图2中图形的角截去,如图3,则由(2)中所得的方法或规律,猜想∠A+∠B+∠C+∠D+∠E+∠F+∠F+∠H+∠M+∠N= °.
22.已知,点E是的中线上一动点,交于点F,连接.
(1)如图1,当点E与点D重合时,求证:;
(2)如图2,当点E与点D不重合时,延长交于点G,交于点H.
①判断四边形的形状,并说明理由;
②如图3,若的边,以为腰作等腰直角,连接,点M为的中点,当点E从点D运动到点A过程中,请直接写出点M的运动路径长.
答案解析部分
1.【答案】A
【解析】【解答】解:A、 既是轴对称图形,又是中心对称图形,故符合题意;
B、是轴对称图形,但不是中心对称图形,故不符合题意;
C、既不是轴对称图形,也不是中心对称图形,故不符合题意;
D、是轴对称图形,但不是中心对称图形,故不符合题意;
故答案为:A.
【分析】中心对称图形:把一个图形绕着某一点旋转180°后,旋转后的图形能够与原来的图形重合,轴对称图形:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形,据此逐项判断即可.
2.【答案】C
【解析】【解答】解:∵黑色是正五边形,
∴一块黑色皮块的内角和为(5-2)×180°=540°.
故答案为:C.
【分析】根据内角和公式(n-2)×180°进行计算.
3.【答案】D
【解析】【解答】解: 在□ABCD中,∠A+∠B=180°,∠D=∠B,
∵∠A:∠B=1:2,
∴∠B=180°×=120°,
∴∠D=∠B=120°.
故答案为:D.
【分析】由平行四边形的性质可得∠A+∠B=180°,∠D=∠B,利用∠A:∠B=1:2求出∠B的度数即可.
4.【答案】D
【解析】【解答】A、两组对角分别相等的四边形是平行四边形,,A错误;
B、一组对边平行,另一组对边相等的四边形可能是等腰梯形,B错误;
C、一组对边相等的四边形不能判断是平行四边形,C错误;
D、一组对边平行且相等的四边形是平行四边形,D正确;
故答案为:D.
【分析】根据平行四边形的判定定理判断即可.
5.【答案】C
【解析】【解答】∵平行四边形的对角线,交于点,已知,,
∴BO=DO=BD=5,CO=AO=AC=3,
∵的周长为15,
∴BC=15-(BO+CO)=15-(5+3)=7,
∴AD=BC=7,
故答案为:C.
【分析】先利用平行四边形的性质可得BO=DO=BD=5,CO=AO=AC=3,再利用三角形的周长公式求出BC的长,最后利用平行四边形的性质可得AD=BC.
6.【答案】D
【解析】【解答】解:∵D是AC的中点,F是CE中点,DF=2,
∴AE=2DF=4,
∵AE=AD,
∴AD=4,
在Rt△ABC中,D为斜边AC的中点,
∴BD=AD=4,
故答案为:D.
【分析】根据三角形的中位线性质可知AE=2DF,从而得知AD=4,再根据直角三角形的中线性质,中线等于斜边的一半可得出答案.
7.【答案】A
【解析】【解答】解:
四边形ABCD是平行四边形
同理:
又
在中,
又
.
故答案为: A.
【分析】本题主要考查了平行四边形的性质、勾股定理.利用可推出: ,再结合可得:,进而推出:,可求出BC的长,得出AD的长,因此根据求出AF的长.利用可推出: ,再结合可得:,进而推出:,代入平行四边形的面积公式:可求出面积.
8.【答案】C
【解析】【解答】解:过点B作BD⊥直线x=4,交直线x=4于点D,作BE⊥x轴,直线x=1与OC交于点M,与x轴交于点F,直线x=4与AB交于点N,如图:
∵四边形OABC是平行四边形,
∴∠OAB=∠BCO,OC∥AB,OA=BC,
∵直线x=1与直线x=4都垂直于x轴,
∴AM∥CN,
∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,
∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC,
在△OAF和△BCD中
∴△OAF≌△BCD(ASA)
∴BD=OF=1,
∴OE=4+1=5,
∴OB=.
∵OE的值是定值,
∴当BE最小时(即B在x轴上),OB取得最小值,最小值OB=OE=5.
故答案为:C.
【分析】过点B作BD⊥直线x=4,交直线x=4于点D,作BE⊥x轴,直线x=1与OC交于点M,与x轴交于点F,直线x=4与AB交于点N,易得OB=,根据四边形OABC是平行四边形可得OA=BC,由平行线的性质可得∠OAF=∠BCD,结合已知用角边角易证△OAF≌△BCD,由OE的值是定值即可得当BE最小时(即B在x轴上),OB取得最小值,最小值OB=OE可求解.
9.【答案】B
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∵EF∥AB,GH∥AD,
∴EF∥AB∥CD,GH∥AD∥BC,
∴四边形AEPH、四边形HPFB、四边形EPGD、四边形GPFC均为平行四边形,
∴S△PDE=S△PDG=S平行四边形PEDG,S△BPH=S△BPF=S平行四边形BFPH,S△ABD=S△CBD=S平行四边形ABCD,
∵S△ABD=S△PDE+S四边形AEPH+S△BPH+S△BDP①,S△CBD=S△PDG+S四边形PGCF+S△BPF-S△BDP②,
∴①-②得S四边形AEPH-S四边形PGCF+2S△BDP=0,
又∵ S四边形AHPE=3,S四边形PFCG=5 ,
∴2S△BDP=5-3,
∴S△BDP=1.
故答案为:B.
【分析】由平行四边形的对边平行得AB∥CD,AD∥BC,由平行于同一直线的两条直线互相平行得EF∥AB∥CD,GH∥AD∥BC,根据两组对边分别平行得四边形是平行四边形得四边形AEPH、四边形HPFB、四边形EPGD、四边形GPFC均为平行四边形,由平行四边形的一条对角线平分平行四边形的面积得S△PDE=S△PDG,S△BPH=S△BPF,S△ABD=S△CBD,进而由割补法可得S△ABD=S△PDE+S四边形AEPH+S△BPH+S△BDP①,S△CBD=S△PDG+S四边形PGCF+S△BPF-S△BDP②,进而根据①-②列出方程可求解.
10.【答案】B
【解析】【解答】解:如图,取BC中点H,连接AH,连接EC交AD于点N,作EM⊥CD交CD的延长线于点M,
∵BC=2AB,BC=2BH=2CH,
∴BA=BH=CH,
又∵∠ABC=60°,
∴△ABH是等边三角形,
∴HA=HB=HC,
∴∠BAC=90°,
∴∠ACB=30°,
∵EC⊥BC,
∠BCD=180°-∠ABC=120°,
∴∠ACE=60°,∠ECM=30°,
∵BC=2AB=8,
∴CD=4,CN=EN=,
∴EC=,EM=,
∴S△BEG=S△BCE+S△ECG-S△BCG=S平行四边形ABCD,
=.
故答案为:B.
【分析】取BC中点H,连接AH,连接EC交AD于点N,作EM⊥CD交CD的延长线于点M,判断出△ABH是等边三角形,得HA=HB=HC,由等边对等角及三角形的内角和定理得∠BAC=90°,进而根据含30°角直角三角形的性质得∠ACB=30°,推出∠ACE=60°,∠ECM=30°,根据平行四边形的性质及轴对称的性质可得EC=,EM=,进而根据S△BEG=S△BCE+S△ECG-S△BCG算出答案.
11.【答案】1440
【解析】【解答】解:由题意得:,
该多边形的内角和为.
故答案为:1440.
【分析】根据多边形的外角和为360°,求出边数,再代入多边形内角和公式,即可得解.
12.【答案】3
【解析】【解答】解:∵四边形ABCD是平行四边形,AB=4cm,AD=7cm,
∴AB=CD=4cm,AB∥CD,BC=AD=7cm,
∴∠ABE=∠F,
∵BF平分∠ABC,
∴∠ABE=∠FBC,
∴∠FBC=∠F,
∴CF=BC=7cm,
∴DF=FC-CD=7-4=3cm;
故答案为:3.
【分析】由平形四边形的性质可得AB=CD=4cm,AB∥CD,BC=AD=7cm,利用平行线的性质及角平分线的定义可得∠FBC=∠F,可得CF=BC=7cm,利用DF=FC-CD即可求解.
13.【答案】
【解析】【解答】∵EA'∥CD,FA'∥BC,
∴,.
又∵∠B+∠D=n°,
∴,
又∵四边形内角和为,
∴,
∴.
故答案为:.
【分析】根据两直线平行,同位角相等,得到,,再利用四边形的内角和等于求解即可.
14.【答案】
【解析】【解答】解:延长CF和AB,交于点H,如下图:
∵四边形ABCD是平行四边形
∴AB∥CD,
∴∠ACD=∠BAC=90°
∴AC=
∵AF平分∠BAC,且CF⊥AF
∴AH=AC=12,FH=FC
∵AB=5
∴BH=12-5=7
∵点E是BC的中点,FH=FC
∴EF=BH=
故答案为:.
【分析】根据平行四边形的性质,可得∠ACD=∠BAC;根据勾股定理,可得AC的长;根据等腰三角形三线合一的性质,可得AH=HC;根据三角形中线的性质,可得EF的长.
15.【答案】
【解析】【解答】解:第1个 的周长为a+b+c
由三角形中位线定理可得:
第2个三角形的周长为(a+b+c),
第3个三角形的周长为×(a+b+c),
第4个三角形的周长为××(a+b+c),
······,
第n个三角形的周长为(a+b+c),
∴ 第次组成的三角形的周长 ;
故答案为: .
【分析】根据三角形中位线定理求解,可得规律第n个三角形的周长为(a+b+c),继而得解.
16.【答案】
【解析】【解答】解:如图,在上截取,连接并延长,作,
四边形是平行四边形,,,
,,
,
,
是等边三角形,
,,
是等边三角形,
,,
,
,
,
,
当点是边延长线上时,点在的延长线上 ,
,,
,
的最小值是,
故答案为:.
【分析】利用瓜豆原理可知点F的运动轨迹是一条直线,故勾手拉手全等三角形模型是本题的解题关键.利用等边三角形的性质通过SAS判定得到,再通过直角三角形的性质求得CM的长度即FC的最小值.
17.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠GAE=∠HCF.
∵点G,H分别是AB ,CD的中点,AB= CD,∴AG=CH.∵AE=CF,
∴△AGE≌△CHF ( SAS),∴GE= HF, ∠AEG= ∠CFH,∴∠GEF =∠HFE,∴GE∥HF.又∵GE=HF,∴四边形EGFH是平行四边形.
(2)解:连结BD交AC于点O,如图.
∵四边形ABCD是平行四边形,
∴OA = OC, OB=0D. BD= 10,
∴ OB=OD=5.∵AE= CF ,OA=OC,
∴ OE=OF.∵AE+CF= EF,
∴2AE= EF=20E,∴AE=OE.又∵点G是AB的中点,∴EG是△ABO
的中位线,∴EG=OB=2.5,∴EG的长为2.5.
【解析】【分析】(1)根据平行四边形的性质可证出△AGE≌△CHF ( SAS),再根据全等三角形的性质可得出GF=HF且GF∥HF,从而证出四边形EGFH是平行四边形;
(2)根据平行四边形的性质和已知 AE+CF=EF ,可知E是OA的中点,所以EG是△ABO的中位线,根据中位线的性质可求出EG的长度.
18.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AD= BC,∠ADC+ ∠BCD =180°.∵PM∥ DC,且PM=DC,∴四边形PMCD是平行四边形,
∴PD=CM,∠PDC+∠DCM= 180°,∴∠ADP= ∠ BCM.在△ADP和△BCM中,,∴△ADP≌△BCM( SAS). .
(2)解:如图,作BH⊥AC于点H,DG⊥AC于点G,∵四边形ABCD是平行四边形,△ABC≌△CDA,∴BH= DG,
∴,即S△BCP = 2S△ABP,,即S△ADP=S△ABP.
∵△ADP≌△BCM,∴S△ADP=S△BCM,∴
【解析】【分析】(1)根据已知条件可知四边形PMCD是平行四边形,则根据平行四边形的性质可证△ADP≌△BCM;
(2)根据四边形ABCD是平行四边形,可知△ABC≌△CDA,从而得到同底边上的高BH= DG,得到S△BCP= 2S△ABP,而△ABP和△ADP是同底等高,所以面积相等,四边形BPCM的面积=△BCP的面积+△ACM的面积,而根据(1)可知△ACM的面积=△ADP的面积,从而可得出答案.
19.【答案】(1)证明:∵AB=AC
∴∠ABC=∠ACB,
∵M是BC的中点,
∴AM⊥BC,
在Rt△ABM和Rt△CBE中,∠MAB+∠ABC=90°,∠ACB+∠EBC=90°,
∴∠MAB=∠EBC,
∵MB=MN,
∴△MBN是等腰直角三角形,
∴∠MNB=∠MBN=45°,
∵∠EBC+∠NBE=∠MAB+∠ABN=∠MNB=45°,
∴∠NBE=∠ABN,即BN平分∠ABE;
(2)解:设BM=CM=MN=a,
∵四边形DNBC是平行四边形,
∴DN=BC=2a,
在△ABN和△DBN中
∴△ABN≌△DBN(SAS)
∴AN=DN=2a,
在Rt△ABM中,由勾股定理可得AM2+BM2=AB2,
即(2a+a)2+a2=1,解得:a=,或a=-(舍去),
∴BC=2a=.
【解析】【分析】(1)由等边对等角可得∠ABC=∠ACB,根据等腰三角形的三线合一可得AM⊥BC,由同角的余角相等可得∠MAB=∠EBC,于是可得△MBN是等腰直角三角形,结合角的构成可求解;
(2)设BM=CM=MN=a,由题意用边角边可证△ABN≌△DBN,由全等三角形的性质可得AN=DN=2a,在Rt△ABM中,由勾股定理可得关于a的方程,然后由BC=2a可求解.
20.【答案】(1)解:∵AC⊥CD,
∴∠ACD=90°,
∵∠ABC=45°,平行四边形ABCD,
∴AB∥CD,
∴∠ABC=∠D=∠DAC=45°,
∴AC=CD,
∵AC2+CD2=AD2即2AC2=36,
∴AC2=18,
∴平行四边形ABCD的面积为AC2=18
(2)证明:过点C作CF⊥CE交BD于点F,
∴∠ECF=90°,
∵AE⊥BD,
∴∠ACD=∠AED=90°,
∴∠ACF+∠FCD=∠ACF+∠ACE=90°,
∴∠ACE=∠FCD,
∵平行四边形ABCD,
∴AB∥CD,
∴∠ABE=∠CDF,
∵∠ABD+∠BAE=∠BAE+∠EAC=90°,
∴∠ABE=∠EAC=∠CDF,
在△ACE和△DCF中
∴△ACE≌△DCF(SAS),
∴CE=CF,DF=AE
∴△CEF是等腰直角三角形,
∴EF2=CE2+CF2=2CE2,
∴,
∵DE=EF+DF,
∴
【解析】【分析】(1)利用垂直的定义可证得∠ACD=90°,利用平行四边形的性质及平行线的性质可证得AC=CD,利用勾股定理求出AC2的值,即可求出平行四边形ABCD的面积.
(2)过点C作CF⊥CE交BD于点F,利用垂直的定义和余角的性质可推出∠ACE=∠FCD,∠ABE=∠EAC=∠CDF,利用SAS证明△ACE≌△DCF,利用全等三角形的性质可证得CE=CF,DF=AE,可推出△CEF是等腰直角三角形,利用勾股定理可证得,然后根据DE=EF+DF,可证得结论.
21.【答案】(1)180
(2)360
(3)1080
【解析】【解答】解:(1)如图1,
∵∠1=∠2+∠D=∠B+∠E+∠D,∠A+∠C+∠1=180°,
∴ ∠A+∠B+∠C+∠D+∠E= ∠A+∠C+∠1=180°;
故答案为:180;
(2)如图2,∵∠2=∠1+∠F=∠B+∠E+∠F,∠A+∠C+∠2+∠D=360°,
∴ ∠A+∠B+∠C+∠D+∠E+∠F= ∠A+∠C+∠2+∠D=360°;
故答案为:360;
(3)由(1)(2)知:每截去一个角则增加180°,当截去5个角时,增加了180°×5的度数,
∴ ∠A+∠B+∠C+∠D+∠E+∠F+∠F+∠H+∠M+∠N=180°+180°×5=1080°.
故答案为:1080.
【分析】(1)根据三角形内角和定理和三角形外角的性质求解即可;
(2)根据三角形外角的性质和四边形内角和等于360°进行解答即可;
(3)由(1)(2)知:每截去一个角则增加180°,当截去5个角时,增加了180°×5的度数,据此即可求解.
22.【答案】(1)证明:,,
,,
为的中线,
,
在与中,
,
,
.
(2)解:①四边形是平行四边形,理由如下:
如图所示,过D作交点Q,连接.
四边形为平行四边形,
.
同(1)可证明,
,
又∵,
四边形是平行四边形;②
【解析】【解答】解:(2)②如图所示,取的中点P,连接,
∵是的中线,即点D为的中点,
∴是的中位线,
∴,
又∵,
∴由平行线的唯一性可知重合,即点E和点P重合,
∴点E为的中点,
∴,
∵四边形使平行四边形,
∴,
∴,
∴四边形是平行四边形,
∴,
∵,
∴;
∵,
∴当点E在上运动时,点F在直线上运动,
∵是等腰直角三角形,
∴,
∴点Q在直线上运动,
如图所示,以点B为原点,以为x轴,y轴建立坐标系,
设,
∴,
∴,
∴,
∴,
∵M为的中点,
∴,
∴点M在直线上运动,
当时,,当时,;
∴点M的运动轨迹是从点沿着直线运动到点,
∴点M的运动路径长为
【分析】 (1)利用ASA可证明△ACD≌△FDB,再利用全等三角形的性质可得AC=DF;
(2)①如图所示,过D作DQ∥EF交BF点Q,连接AQ,先证明四边形DEFQ为平行四边形,得到DQ=EF,同(1)可证明AC=DQ,得到AC=EF,由此即可四边形ACEF是平行四边形;
②如图所示,取CH的中点P,连接DP,利用平行四边形的性质和判定说明AE=FH,再依次说明点E在AD上运动时,点F在直线BF上运动,点Q在直线BQ上运动,点M在直线上运动,求得M点的运动轨迹为从点沿着直线运动到点,最后利用勾股定理求得点M的运动路径长.
1 / 1
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
