矩形的性质与判定复习(浙江省衢州市开化县)
文档属性
| 名称 | 矩形的性质与判定复习(浙江省衢州市开化县) |
|
|
| 格式 | rar | ||
| 文件大小 | 202.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-05 00:00:00 | ||
图片预览



文档简介
课件14张PPT。13 March 2019浙江省领雁工程指导老师:翁 强矩形的性质与判定复习13 March 2019复习回顾:矩形1、定义:有一个角是 的 叫矩形。2、性质和判定:同平行四边形平行四边形直角四个角都是直角对角线相等且互相平分3、对角线相等的平行四边形.2、有三个角是直角的四边形.1、有一个角是直角的平行四边形.ABCD∟∟∟∟O13 March 20193、直角三角形的性质及判定方法:角:直角三角形两锐角互余。线段:边角关系:1、勾股定理:两直角边的平方和等于斜边
的平方。2、斜边中线的性质:直角三角形斜边中线
等于斜边的一半。1、直角三角形中,30°角所对的直角边
等于斜边的一半。2、直角三角形中,若直角边等于斜边的一半,
那么这条直角边所对的角等于30°。链接:直角三角形ABCD1、已知矩形的一条对角线与一边的夹角
是40°,则两条对角线所成的锐角的
度数是( )
A、100° B、90° C、80° D、70°热身运动2、矩形的一边长为6,各边中点围成的四
边形的周长是20 ,则矩形的对角线长
为 ,面积为 。热身运动3、平行四边形四个内角的平分线,如果能围成
一个四边形,那么这个四边形一定是( )
A、矩形 B、菱形
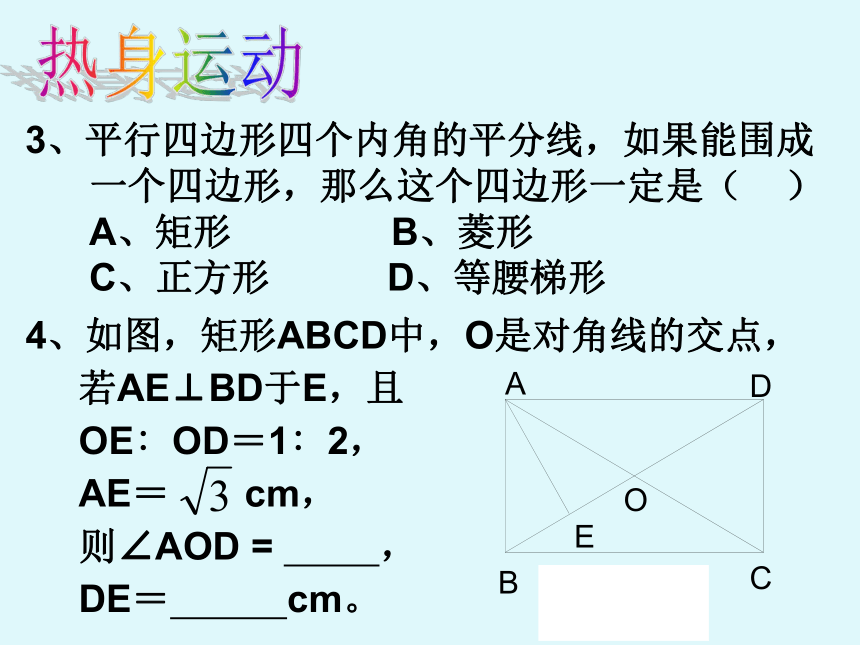
C、正方形 D、等腰梯形4、如图,矩形ABCD中,O是对角线的交点,
若AE⊥BD于E,且
OE∶OD=1∶2,
AE= cm,
则∠AOD = ,
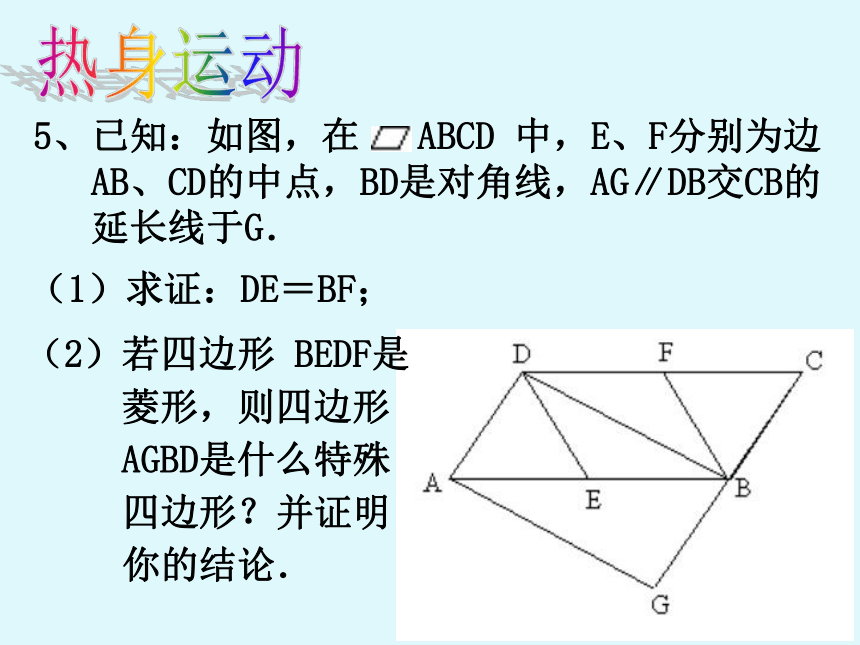
DE= cm。5、已知:如图,在 ABCD 中,E、F分别为边
AB、CD的中点,BD是对角线,AG∥DB交CB的
延长线于G.(1)求证:DE=BF;(2)若四边形 BEDF是
菱形,则四边形
AGBD是什么特殊
四边形?并证明
你的结论. 热身运动 给你一张矩形的纸片,你能折叠出一个菱形吗?能折叠出一个正方形吗?课外兴趣题:动一动,想一想1、如图,将矩形ABCD沿AE折叠,使点D落
在BC边上的F点处。矩形中的折叠问题(1)若∠BAF=60°,求∠EAF的度数;(2)若AB=6cm,
AD=10cm,
求线段CE的
长及△AEF的
面积.2、如图,矩形纸片ABCD中,现将A、C重合,使纸片折叠压平,设折痕为EF。(1)连结CF,四边形AECF是什么特殊的四边形?为什么?(2)若AB=4cm,AD=8cm,你能求出线段BE及折痕EF的长吗?矩形中的折叠问题3、在平面直角坐标系中,矩形OABC的两边OA、OC分别落在x轴,y轴上,且OA=4,0C=3。(1)求对角线OB所在直线的解析式;OCABxy3、在平面直角坐标系中,矩形OABC的两边OA、OC分别落在x轴,y轴上,且OA=4,0C=3。(2)如图,将△OAB沿对角线OB翻折得到△OBN,ON与AB交于点M。OCABxy② 试求直线MN的解析式. ① 判断△OBM是什么三角形,并说明理由; 1、给你一张矩形的纸片,你能折叠出一个菱形吗?能折叠出一个正方形吗?课外兴趣题:动一动,想一想2、如图,P是矩形ABCD内一点,
PA=3,PD=4,PC=5,
则PB= 。EF课外兴趣题:动一动,想一想提示:过点P作其中一边的垂线,利用勾股定理来解。再 见
的平方。2、斜边中线的性质:直角三角形斜边中线
等于斜边的一半。1、直角三角形中,30°角所对的直角边
等于斜边的一半。2、直角三角形中,若直角边等于斜边的一半,
那么这条直角边所对的角等于30°。链接:直角三角形ABCD1、已知矩形的一条对角线与一边的夹角
是40°,则两条对角线所成的锐角的
度数是( )
A、100° B、90° C、80° D、70°热身运动2、矩形的一边长为6,各边中点围成的四
边形的周长是20 ,则矩形的对角线长
为 ,面积为 。热身运动3、平行四边形四个内角的平分线,如果能围成
一个四边形,那么这个四边形一定是( )
A、矩形 B、菱形
C、正方形 D、等腰梯形4、如图,矩形ABCD中,O是对角线的交点,
若AE⊥BD于E,且
OE∶OD=1∶2,
AE= cm,
则∠AOD = ,
DE= cm。5、已知:如图,在 ABCD 中,E、F分别为边
AB、CD的中点,BD是对角线,AG∥DB交CB的
延长线于G.(1)求证:DE=BF;(2)若四边形 BEDF是
菱形,则四边形
AGBD是什么特殊
四边形?并证明
你的结论. 热身运动 给你一张矩形的纸片,你能折叠出一个菱形吗?能折叠出一个正方形吗?课外兴趣题:动一动,想一想1、如图,将矩形ABCD沿AE折叠,使点D落
在BC边上的F点处。矩形中的折叠问题(1)若∠BAF=60°,求∠EAF的度数;(2)若AB=6cm,
AD=10cm,
求线段CE的
长及△AEF的
面积.2、如图,矩形纸片ABCD中,现将A、C重合,使纸片折叠压平,设折痕为EF。(1)连结CF,四边形AECF是什么特殊的四边形?为什么?(2)若AB=4cm,AD=8cm,你能求出线段BE及折痕EF的长吗?矩形中的折叠问题3、在平面直角坐标系中,矩形OABC的两边OA、OC分别落在x轴,y轴上,且OA=4,0C=3。(1)求对角线OB所在直线的解析式;OCABxy3、在平面直角坐标系中,矩形OABC的两边OA、OC分别落在x轴,y轴上,且OA=4,0C=3。(2)如图,将△OAB沿对角线OB翻折得到△OBN,ON与AB交于点M。OCABxy② 试求直线MN的解析式. ① 判断△OBM是什么三角形,并说明理由; 1、给你一张矩形的纸片,你能折叠出一个菱形吗?能折叠出一个正方形吗?课外兴趣题:动一动,想一想2、如图,P是矩形ABCD内一点,
PA=3,PD=4,PC=5,
则PB= 。EF课外兴趣题:动一动,想一想提示:过点P作其中一边的垂线,利用勾股定理来解。再 见
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
