浙教版七年级数学上册试题 4.2 代数式(含解析)
文档属性
| 名称 | 浙教版七年级数学上册试题 4.2 代数式(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 263.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 08:08:06 | ||
图片预览



文档简介
4.2 代数式
一、单选题
1.下列各式中,不是代数式的是( )
A.-3 B. C. D.
2.下列代数式书写规范的是( )
A. B. C. D.÷
3.代数式的意义是( ).
A.的平方与的和 B.与的平方的和
C.与两数的平方和 D.与的和的平方
4.下列关于“代数式”的意义叙述正确的有( )个.
①x的4倍与y的2倍的和是;
②小明以x米/分钟的速度跑了4分钟,再以y米/分钟的速度步行了2分钟,小明一共走了米;
③苹果每千克x元,橘子每千克y元,买4千克橘子、2千克苹果一共花费元.
A.3 B.2 C.1 D.0
5.下列说法中,正确的是( )
A.表示x,y,3,的积的代数式为3xy
B.a是代数式,1不是代数式
C.的意义是a与3的差除b的商
D.m,n两数的差的平方与m,n两数积的2倍的和表示为(m-n)2+2mn
6.新冠疫情期间间,某药店店对一品牌橡胶手套进行优惠促销,将原价m元的橡胶手套每盒以()元售出,则以下四种说法中可以准确表达该药店促销方法的是
A.将原价打6折之后,再降低8元 B.将原价降低8元之后,再打3折
C.将原价降低8元之后,再打6折 D.将原价打8折之后,再降低6元
7.按一定规律排列的多项式:,,,,…,第n
个多项式是( ).
A. B.
C. D.
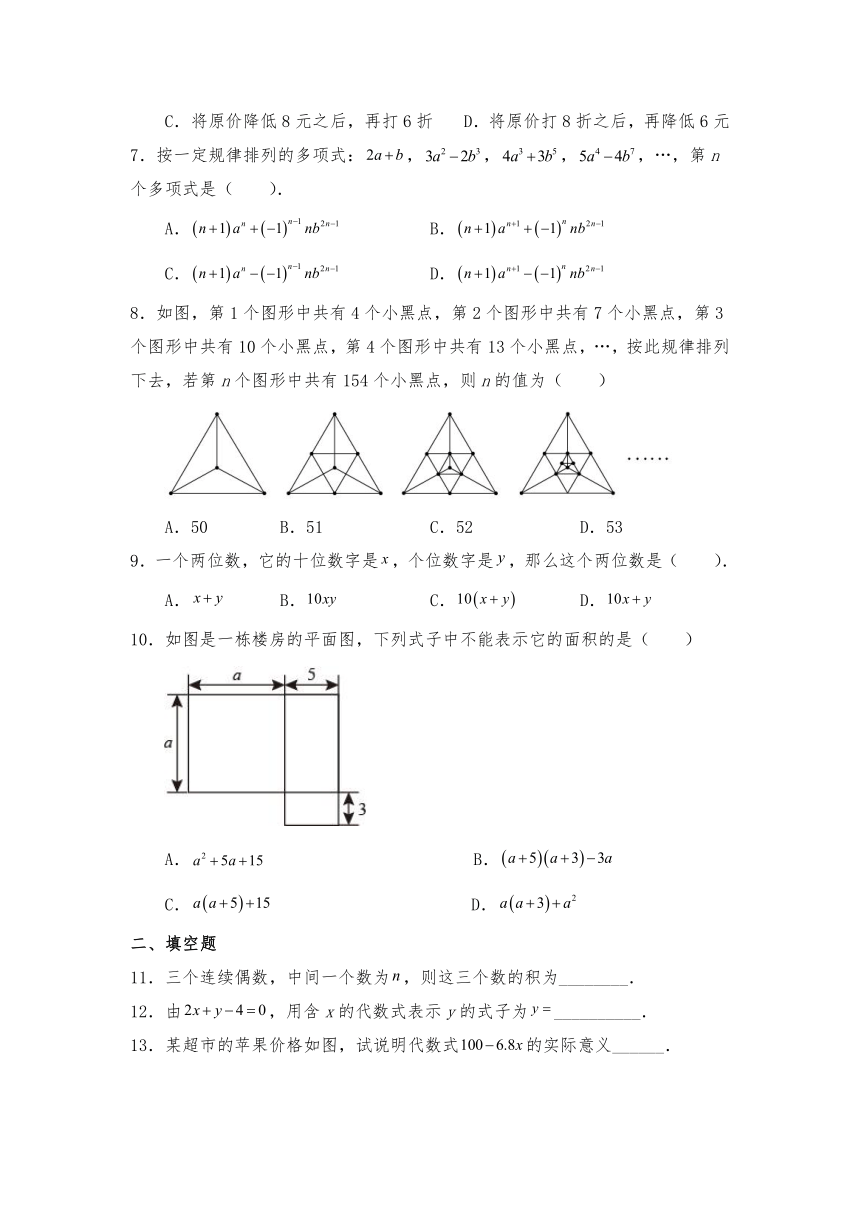
8.如图,第1个图形中共有4个小黑点,第2个图形中共有7个小黑点,第3个图形中共有10个小黑点,第4个图形中共有13个小黑点,…,按此规律排列下去,若第n个图形中共有154个小黑点,则n的值为( )
A.50 B.51 C.52 D.53
9.一个两位数,它的十位数字是,个位数字是,那么这个两位数是( ).
A. B. C. D.
10.如图是一栋楼房的平面图,下列式子中不能表示它的面积的是( )
A. B.
C. D.
二、填空题
11.三个连续偶数,中间一个数为,则这三个数的积为________.
12.由,用含x的代数式表示y的式子为__________.
13.某超市的苹果价格如图,试说明代数式的实际意义______.
14.对代数式“5x”,我们可以这样解释:香蕉每千克5元,某人买了x千克,共付款5x元.请你对代数式“”给出一个实际生活方面的合理解释:______.
15.一台扫描仪的成本价为n元,销售价比成本价提高了30%,为尽快打开市场.按销售价的八折优惠出售,则优惠后每台扫描仪的实际售价为______元.
16.某商店经销一种品牌的空调,其中某一种型号的空调每台进价为a元,在夏季销售高峰时,商店将售价提高20%后进行销售,一段时间后,商店又在此基础上降价20%进行促销,这时该型号空调的零售价为_________元
17.我国的《洛书》中记载着世界上最古老的一个幻方:将1-9这九个数字填入3×3的方格内,使三行、三列、两对角线上的三个数之和都是15,如图所示幻方中,字母m所表示的数是______.
18.猜数字游戏中,小明写出如下一组数:,根据此规律,第个数是__________(为正整数).
19.用字母表示数的书写规则:
(1)字母与字母相乘时,“×”号通常省略不写或写成“ ______ ”;
(2)字母与数相乘时,数通常写在字母的__________;
(3)带分数与字母相乘时,通常化带分数为___________;
(4)字母与字母相除时,要写成__________的形式;
20.如果某种药品降价40%后的价格为a元,那么这种药品降价前的价格为______元.
21.甲、乙两地相距400千米,某车以80千米/小时的速度从甲地开往乙地,行驶了t(t≤5)小时,此时该车距乙地的路程为____________千米.
三、解答题
22.在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是,小正方形的边长是,用式子表示剩余部分的面积.
23.学校开展“为灾区儿童献爱心”活动,五年级同学捐款450元,六年级捐款数是五年级的,又恰好占全校捐款总数的;全校同学一共捐款多少元?
24.绕着一个圆锥形状的碎石堆外边缘走一圈,要走18.84米,如果这堆碎石的高是4米.(取3.14)
(1)这堆碎石的体积是多少立方米?
(2)旧城道路改造需要用这堆碎石铺路.要用这些碎石铺一条厚度30厘米,宽2米的路,可以铺长为多少米的路?
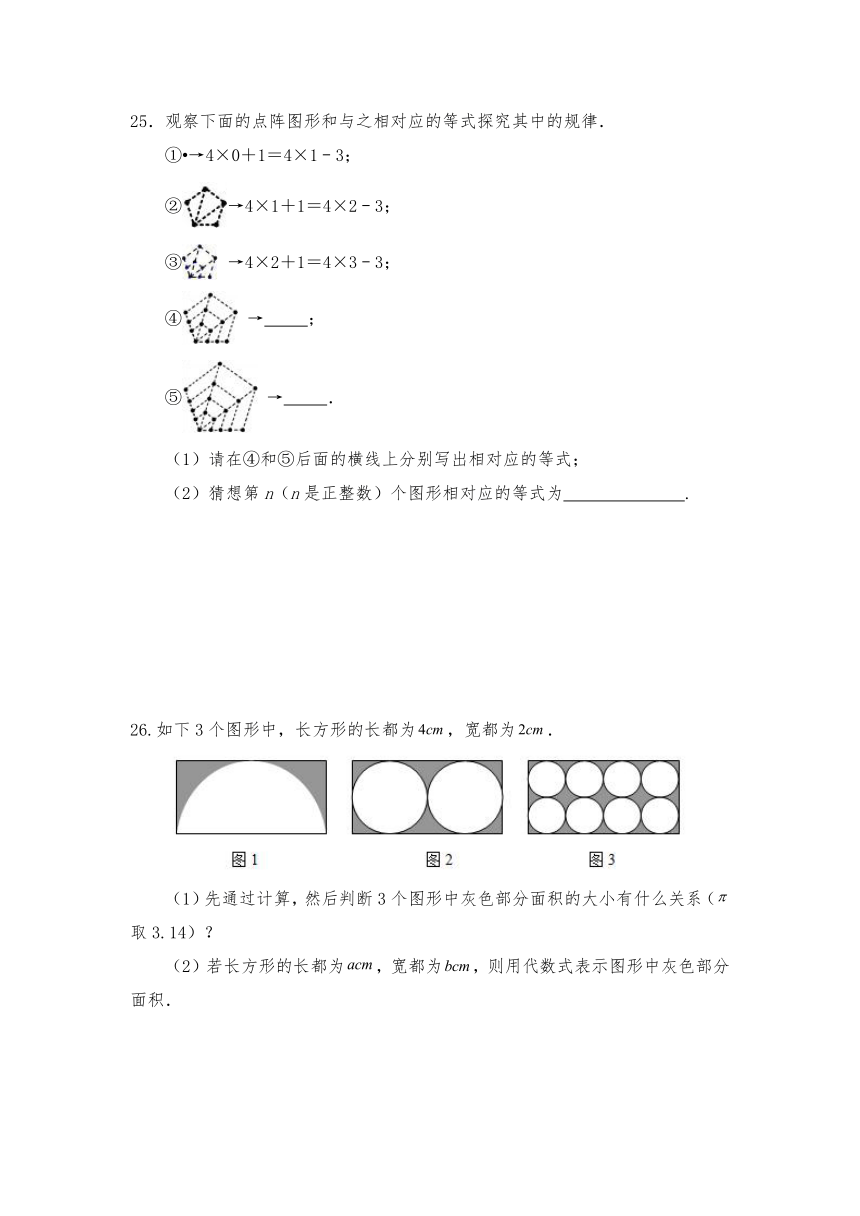
25.观察下面的点阵图形和与之相对应的等式探究其中的规律.
① →4×0+1=4×1﹣3;
②→4×1+1=4×2﹣3;
③ →4×2+1=4×3﹣3;
④ → ;
⑤ → .
(1)请在④和⑤后面的横线上分别写出相对应的等式;
(2)猜想第n(n是正整数)个图形相对应的等式为 .
26.如下3个图形中,长方形的长都为,宽都为.
(1)先通过计算,然后判断3个图形中灰色部分面积的大小有什么关系(取3.14)?
(2)若长方形的长都为,宽都为,则用代数式表示图形中灰色部分面积.
27.静脉输液是用来给病人注射液体和药品的.在医院里,静脉输液是护士护理中最重要的一项工作,护士需要依据输液速率D,即每分钟输入多少滴液体,来计算输完点滴注射液的时间t(单位:分钟).他们使用的公式是:,其中,V 是点滴注射液的容积,以毫升(ml)为单位,d 是点滴系数,即每毫升(ml)液体的滴数.
(1)一瓶点滴注射液的容积为360毫升,点滴系数是每毫升25 滴,如果护士给病人注射的输液速率为每分钟50滴,那么输完这瓶点滴注射液需要多少分钟?
(2)如果遇到的病人年龄比较大时,护士会把输液速率缩小为原来的,请准确地描述,在V 和 d 保持不变的条件下,输完这瓶点滴注射液的时间将会发生怎样的变化?
答案
一、单选题
1.C
【分析】
代数式是由运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连接而成的式子.根据代数式的定义逐项判断即可
解:A选项:-3是代数式,不符合题意
B选项:是代数式,不符合题意
C选项:是方程,不是代数式,符合题意
D选项:是代数式,不符合题意
故选:C
2.A
【分析】
根据代数式的书写要求判断各项即可得出正确答案.
解:A.书写正确,该选项符合题意;
B.正确的书写为,该选项不符合题意;
C.正确的书写为,该选项不符合题意;
D.正确的书写为,该选项不符合题意;
故选:A.
3.C
【分析】
说出代数式的意义,实际上就是把代数式用语言叙述出来。叙述时,要求既要表明运算的顺序,又要说出运算的最终结果.
解:代数式的意义是a与b两数的平方的和.
故选:C.
4.B
【分析】
根据代数式的意义分别对三个叙述进行判断即可.
解:①x的4倍与y的2倍的和是,正确;
②小明以x米/分钟的速度跑了4分钟,再以y米/分钟的速度步行了2分钟,小明一共走了米,正确;
③苹果每千克x元,橘子每千克y元,买4千克橘子、2千克苹果一共花费元,错误;
故正确的有2个
故选:B.
5.D
【分析】
根据代数式的定义,以及代数式的书写,以及根据题意列出对应的代数式,然后进行判断即可.
解:A、表示x,y,3,的积的代数式为,故此选项不符合题意;
B、a是代数式,1也是代数式,故此选项不符合题意;
C、的意义是a与3的差除以b的商,故此选项不符合题意;
D、m,n两数的差的平方为,m,n两数积的2倍为,则m,n两数的差的平方与m,n两数积的2倍的和表示为(m-n)2+2mn,故此选项符合题意;
故选D.
6.A
【分析】
根据原价和售价的关系,可得答案.
解:售价为(),是原价m乘以0.6,再减去8,
由此可得,促销方式为将原价打6折之后,再降低8元,
故选A
7.A
【分析】
从两个方面(系数、指数)总结规律,即可求解.
解:通过观察即可发现:
a的系数规律为:n+1,
a的指数的规律为:n,
b的系数规律为:,
b的指数的规律为:2n-1,
综合后,第n个多项式为:,
故选:A.
8.B
【分析】
观察图形的变化可得后一个图形小黑点的个数比前一个图形的小黑点的个数多3,进而可得第个图形中小黑点的个数规律为.
解:第①个图形中共有4个小黑点,即3=3×1+1;
第②个图形中共有7个小黑点,即7=3×2+1;
第③个图形中共有10个小黑点,即10=3×3+1;
…,
按此规律排列下去,则第个图形中小黑点的个数规律为,
,解得,
故选:B.
9.D
【分析】
根据两位数的表示方法:十位数字×10+个位数字,即可解答
解:∵一个两位数,它的十位数是,个位数字是
∴根据两位数的表示方法,这个两位数表示为:
故选:D
10.D
【分析】
分别用不用的方法表示楼房的面积,逐个排除即可得到正确的答案.
解:A.是三个图形面积的和,正确,不符合题意;
B.是补成一个大长方形,用大长方形的面积减去补的长方形的面积,正确,不符合题意;
C.是上面大长方形的面积加上下面小长方形的面积,正确,不符合题意;
D.不是楼房的面积,错误,符合题意.
故选:D.
二、填空题
11.
【分析】
根据连续偶数之间的差值为2可求.
解:三个连续偶数,中间一个数为
前一个偶数为:,后一个偶数为:
三个数的积为:
故答案为:.
12.y=-2x+4
【分析】
先移项,用含x的代数式表示y,即可得到答案.
解:∵
∴y=-2x+4
故答案为:y=-2x+4.
13.用100元钱买了x斤6.8元/斤的苹果,还剩多少钱?(答案不唯一,合理即可)
【分析】
根据所给图的信息和代数式结构解释,合理即可.
解:根据题意,可以解释为:用100元钱买了x斤6.8元/斤的苹果,还剩多少钱?
故答案为:用100元钱买了x斤6.8元/斤的苹果,还剩多少钱?(答案不唯一,合理即可).
14.一个西瓜的质量是a千克,一个桃子的质量是b千克,那么两个西瓜和一个桃子的质量共千克,答案不唯一.
【分析】
对多项式“”,是2与a的积与b的和,表示生活中两类的相乘后的和计算.比如:一个西瓜的质量是a千克,一个桃子的质量是b千克,那么两个西瓜和一个桃子的质量共千克.
解:一个西瓜的质量是a千克,一个桃子的质量是b千克,那么两个西瓜和一个桃子的质量共千克.
故答案为:一个西瓜的质量是a千克,一个桃子的质量是b千克,那么两个西瓜和一个桃子的质量共千克,答案不唯一.
15.
【分析】
根据题意可以用代数式表示出优惠后的每台扫描仪的实际售价.
解:由题意有,优惠后每台扫描仪的售价为:n×(1+30%)×80%=1.04n,
故答案为:1.04n.
16.0.96a
【分析】
空调每台进价为a元,商店将售价提高20%后a(1+20%),商店又在此基础上降价20%进行促销此时a (1+20%)(1-20%),化简即可,
解:a (1+20%)(1-20%)=0.96a
故答案为:0.96a,
17.4
【分析】
根据“每行、每列、每条对角线上的三个数之和相等”解答即可.
解:根据“每行、每列、每条对角线上的三个数之和相等”,
可知三行、三列、两对角线上的三个数之和都等于15,
∴第一列第三个数为:15-2-5=8,
∴m=15-8-3=4.
故答案为:4.
18.
【分析】
根据题意已知可得分数的分子是2n,分母是2n+3,进而得出答案即可.
解:∵分数的分子分别是:2,2 2=4,23=8,24=16,…
分数的分母分别是:2+3=5,2 2+3=7,23+3=11,24+3=19,…
∴第n个数是(为正整数).
故答案为:.
19. 前面 假分数 分数
略
20.
【分析】
降价40%后的价格为a元,则降价前的价格的60%是a元,据此即可求解.
解:a÷(1﹣40%)=a,
故答案是:a.
21.(400﹣80t)
【分析】
甲、乙两地相距400千米,减去汽车行走的路程即可求解.
解:依题意可知,该车距乙地的路程为(400﹣80t)千米.
故答案为:(400﹣80t).
三、解答题
22.
解:∵大正方形的面积为,小正方形的面积为,
∴剩余部分的面积为.
23.
解:五年级同学捐款450元,六年级捐款数是五年级的,
∴六年级捐款元,
∵六年级捐款恰好占全校捐款总数的,
∴全校捐款为元,
答:全校捐款2520元.
24.
解:(1)×3.14×(18.84÷3.14÷2)2×4=×3.14×9×4=37.68(立方米);
(2)30厘米=0.3米,
(米).
25.
解:①;
②;
③;
④,
⑤;
(2)第个图形:.
26.
解:(1)第一个的灰色部分面积是长方形与半圆的差:;
第二个为长方形与两个小圆的差:;
第三个为长方形与八个小圆的差:
∴它们都相等.
故答案为:相等.
(2)若长方形的长都为,宽都为,
则第一个图形中灰色部分面积为:;
则第二个图形中灰色部分面积为:;
则第三个图形中灰色部分面积为:;
∴三个图形中灰色部分面积都相等,用代数式表示为:,
故答案为:.
27.
解:(1)
答:输完这瓶点滴注射液需要180分钟。
(2)设护士给年龄比较大的病人输液速率为,根据题意得
答:输完这瓶点滴注射液的时间将会变为原来的2倍。
一、单选题
1.下列各式中,不是代数式的是( )
A.-3 B. C. D.
2.下列代数式书写规范的是( )
A. B. C. D.÷
3.代数式的意义是( ).
A.的平方与的和 B.与的平方的和
C.与两数的平方和 D.与的和的平方
4.下列关于“代数式”的意义叙述正确的有( )个.
①x的4倍与y的2倍的和是;
②小明以x米/分钟的速度跑了4分钟,再以y米/分钟的速度步行了2分钟,小明一共走了米;
③苹果每千克x元,橘子每千克y元,买4千克橘子、2千克苹果一共花费元.
A.3 B.2 C.1 D.0
5.下列说法中,正确的是( )
A.表示x,y,3,的积的代数式为3xy
B.a是代数式,1不是代数式
C.的意义是a与3的差除b的商
D.m,n两数的差的平方与m,n两数积的2倍的和表示为(m-n)2+2mn
6.新冠疫情期间间,某药店店对一品牌橡胶手套进行优惠促销,将原价m元的橡胶手套每盒以()元售出,则以下四种说法中可以准确表达该药店促销方法的是
A.将原价打6折之后,再降低8元 B.将原价降低8元之后,再打3折
C.将原价降低8元之后,再打6折 D.将原价打8折之后,再降低6元
7.按一定规律排列的多项式:,,,,…,第n
个多项式是( ).
A. B.
C. D.
8.如图,第1个图形中共有4个小黑点,第2个图形中共有7个小黑点,第3个图形中共有10个小黑点,第4个图形中共有13个小黑点,…,按此规律排列下去,若第n个图形中共有154个小黑点,则n的值为( )
A.50 B.51 C.52 D.53
9.一个两位数,它的十位数字是,个位数字是,那么这个两位数是( ).
A. B. C. D.
10.如图是一栋楼房的平面图,下列式子中不能表示它的面积的是( )
A. B.
C. D.
二、填空题
11.三个连续偶数,中间一个数为,则这三个数的积为________.
12.由,用含x的代数式表示y的式子为__________.
13.某超市的苹果价格如图,试说明代数式的实际意义______.
14.对代数式“5x”,我们可以这样解释:香蕉每千克5元,某人买了x千克,共付款5x元.请你对代数式“”给出一个实际生活方面的合理解释:______.
15.一台扫描仪的成本价为n元,销售价比成本价提高了30%,为尽快打开市场.按销售价的八折优惠出售,则优惠后每台扫描仪的实际售价为______元.
16.某商店经销一种品牌的空调,其中某一种型号的空调每台进价为a元,在夏季销售高峰时,商店将售价提高20%后进行销售,一段时间后,商店又在此基础上降价20%进行促销,这时该型号空调的零售价为_________元
17.我国的《洛书》中记载着世界上最古老的一个幻方:将1-9这九个数字填入3×3的方格内,使三行、三列、两对角线上的三个数之和都是15,如图所示幻方中,字母m所表示的数是______.
18.猜数字游戏中,小明写出如下一组数:,根据此规律,第个数是__________(为正整数).
19.用字母表示数的书写规则:
(1)字母与字母相乘时,“×”号通常省略不写或写成“ ______ ”;
(2)字母与数相乘时,数通常写在字母的__________;
(3)带分数与字母相乘时,通常化带分数为___________;
(4)字母与字母相除时,要写成__________的形式;
20.如果某种药品降价40%后的价格为a元,那么这种药品降价前的价格为______元.
21.甲、乙两地相距400千米,某车以80千米/小时的速度从甲地开往乙地,行驶了t(t≤5)小时,此时该车距乙地的路程为____________千米.
三、解答题
22.在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是,小正方形的边长是,用式子表示剩余部分的面积.
23.学校开展“为灾区儿童献爱心”活动,五年级同学捐款450元,六年级捐款数是五年级的,又恰好占全校捐款总数的;全校同学一共捐款多少元?
24.绕着一个圆锥形状的碎石堆外边缘走一圈,要走18.84米,如果这堆碎石的高是4米.(取3.14)
(1)这堆碎石的体积是多少立方米?
(2)旧城道路改造需要用这堆碎石铺路.要用这些碎石铺一条厚度30厘米,宽2米的路,可以铺长为多少米的路?
25.观察下面的点阵图形和与之相对应的等式探究其中的规律.
① →4×0+1=4×1﹣3;
②→4×1+1=4×2﹣3;
③ →4×2+1=4×3﹣3;
④ → ;
⑤ → .
(1)请在④和⑤后面的横线上分别写出相对应的等式;
(2)猜想第n(n是正整数)个图形相对应的等式为 .
26.如下3个图形中,长方形的长都为,宽都为.
(1)先通过计算,然后判断3个图形中灰色部分面积的大小有什么关系(取3.14)?
(2)若长方形的长都为,宽都为,则用代数式表示图形中灰色部分面积.
27.静脉输液是用来给病人注射液体和药品的.在医院里,静脉输液是护士护理中最重要的一项工作,护士需要依据输液速率D,即每分钟输入多少滴液体,来计算输完点滴注射液的时间t(单位:分钟).他们使用的公式是:,其中,V 是点滴注射液的容积,以毫升(ml)为单位,d 是点滴系数,即每毫升(ml)液体的滴数.
(1)一瓶点滴注射液的容积为360毫升,点滴系数是每毫升25 滴,如果护士给病人注射的输液速率为每分钟50滴,那么输完这瓶点滴注射液需要多少分钟?
(2)如果遇到的病人年龄比较大时,护士会把输液速率缩小为原来的,请准确地描述,在V 和 d 保持不变的条件下,输完这瓶点滴注射液的时间将会发生怎样的变化?
答案
一、单选题
1.C
【分析】
代数式是由运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连接而成的式子.根据代数式的定义逐项判断即可
解:A选项:-3是代数式,不符合题意
B选项:是代数式,不符合题意
C选项:是方程,不是代数式,符合题意
D选项:是代数式,不符合题意
故选:C
2.A
【分析】
根据代数式的书写要求判断各项即可得出正确答案.
解:A.书写正确,该选项符合题意;
B.正确的书写为,该选项不符合题意;
C.正确的书写为,该选项不符合题意;
D.正确的书写为,该选项不符合题意;
故选:A.
3.C
【分析】
说出代数式的意义,实际上就是把代数式用语言叙述出来。叙述时,要求既要表明运算的顺序,又要说出运算的最终结果.
解:代数式的意义是a与b两数的平方的和.
故选:C.
4.B
【分析】
根据代数式的意义分别对三个叙述进行判断即可.
解:①x的4倍与y的2倍的和是,正确;
②小明以x米/分钟的速度跑了4分钟,再以y米/分钟的速度步行了2分钟,小明一共走了米,正确;
③苹果每千克x元,橘子每千克y元,买4千克橘子、2千克苹果一共花费元,错误;
故正确的有2个
故选:B.
5.D
【分析】
根据代数式的定义,以及代数式的书写,以及根据题意列出对应的代数式,然后进行判断即可.
解:A、表示x,y,3,的积的代数式为,故此选项不符合题意;
B、a是代数式,1也是代数式,故此选项不符合题意;
C、的意义是a与3的差除以b的商,故此选项不符合题意;
D、m,n两数的差的平方为,m,n两数积的2倍为,则m,n两数的差的平方与m,n两数积的2倍的和表示为(m-n)2+2mn,故此选项符合题意;
故选D.
6.A
【分析】
根据原价和售价的关系,可得答案.
解:售价为(),是原价m乘以0.6,再减去8,
由此可得,促销方式为将原价打6折之后,再降低8元,
故选A
7.A
【分析】
从两个方面(系数、指数)总结规律,即可求解.
解:通过观察即可发现:
a的系数规律为:n+1,
a的指数的规律为:n,
b的系数规律为:,
b的指数的规律为:2n-1,
综合后,第n个多项式为:,
故选:A.
8.B
【分析】
观察图形的变化可得后一个图形小黑点的个数比前一个图形的小黑点的个数多3,进而可得第个图形中小黑点的个数规律为.
解:第①个图形中共有4个小黑点,即3=3×1+1;
第②个图形中共有7个小黑点,即7=3×2+1;
第③个图形中共有10个小黑点,即10=3×3+1;
…,
按此规律排列下去,则第个图形中小黑点的个数规律为,
,解得,
故选:B.
9.D
【分析】
根据两位数的表示方法:十位数字×10+个位数字,即可解答
解:∵一个两位数,它的十位数是,个位数字是
∴根据两位数的表示方法,这个两位数表示为:
故选:D
10.D
【分析】
分别用不用的方法表示楼房的面积,逐个排除即可得到正确的答案.
解:A.是三个图形面积的和,正确,不符合题意;
B.是补成一个大长方形,用大长方形的面积减去补的长方形的面积,正确,不符合题意;
C.是上面大长方形的面积加上下面小长方形的面积,正确,不符合题意;
D.不是楼房的面积,错误,符合题意.
故选:D.
二、填空题
11.
【分析】
根据连续偶数之间的差值为2可求.
解:三个连续偶数,中间一个数为
前一个偶数为:,后一个偶数为:
三个数的积为:
故答案为:.
12.y=-2x+4
【分析】
先移项,用含x的代数式表示y,即可得到答案.
解:∵
∴y=-2x+4
故答案为:y=-2x+4.
13.用100元钱买了x斤6.8元/斤的苹果,还剩多少钱?(答案不唯一,合理即可)
【分析】
根据所给图的信息和代数式结构解释,合理即可.
解:根据题意,可以解释为:用100元钱买了x斤6.8元/斤的苹果,还剩多少钱?
故答案为:用100元钱买了x斤6.8元/斤的苹果,还剩多少钱?(答案不唯一,合理即可).
14.一个西瓜的质量是a千克,一个桃子的质量是b千克,那么两个西瓜和一个桃子的质量共千克,答案不唯一.
【分析】
对多项式“”,是2与a的积与b的和,表示生活中两类的相乘后的和计算.比如:一个西瓜的质量是a千克,一个桃子的质量是b千克,那么两个西瓜和一个桃子的质量共千克.
解:一个西瓜的质量是a千克,一个桃子的质量是b千克,那么两个西瓜和一个桃子的质量共千克.
故答案为:一个西瓜的质量是a千克,一个桃子的质量是b千克,那么两个西瓜和一个桃子的质量共千克,答案不唯一.
15.
【分析】
根据题意可以用代数式表示出优惠后的每台扫描仪的实际售价.
解:由题意有,优惠后每台扫描仪的售价为:n×(1+30%)×80%=1.04n,
故答案为:1.04n.
16.0.96a
【分析】
空调每台进价为a元,商店将售价提高20%后a(1+20%),商店又在此基础上降价20%进行促销此时a (1+20%)(1-20%),化简即可,
解:a (1+20%)(1-20%)=0.96a
故答案为:0.96a,
17.4
【分析】
根据“每行、每列、每条对角线上的三个数之和相等”解答即可.
解:根据“每行、每列、每条对角线上的三个数之和相等”,
可知三行、三列、两对角线上的三个数之和都等于15,
∴第一列第三个数为:15-2-5=8,
∴m=15-8-3=4.
故答案为:4.
18.
【分析】
根据题意已知可得分数的分子是2n,分母是2n+3,进而得出答案即可.
解:∵分数的分子分别是:2,2 2=4,23=8,24=16,…
分数的分母分别是:2+3=5,2 2+3=7,23+3=11,24+3=19,…
∴第n个数是(为正整数).
故答案为:.
19. 前面 假分数 分数
略
20.
【分析】
降价40%后的价格为a元,则降价前的价格的60%是a元,据此即可求解.
解:a÷(1﹣40%)=a,
故答案是:a.
21.(400﹣80t)
【分析】
甲、乙两地相距400千米,减去汽车行走的路程即可求解.
解:依题意可知,该车距乙地的路程为(400﹣80t)千米.
故答案为:(400﹣80t).
三、解答题
22.
解:∵大正方形的面积为,小正方形的面积为,
∴剩余部分的面积为.
23.
解:五年级同学捐款450元,六年级捐款数是五年级的,
∴六年级捐款元,
∵六年级捐款恰好占全校捐款总数的,
∴全校捐款为元,
答:全校捐款2520元.
24.
解:(1)×3.14×(18.84÷3.14÷2)2×4=×3.14×9×4=37.68(立方米);
(2)30厘米=0.3米,
(米).
25.
解:①;
②;
③;
④,
⑤;
(2)第个图形:.
26.
解:(1)第一个的灰色部分面积是长方形与半圆的差:;
第二个为长方形与两个小圆的差:;
第三个为长方形与八个小圆的差:
∴它们都相等.
故答案为:相等.
(2)若长方形的长都为,宽都为,
则第一个图形中灰色部分面积为:;
则第二个图形中灰色部分面积为:;
则第三个图形中灰色部分面积为:;
∴三个图形中灰色部分面积都相等,用代数式表示为:,
故答案为:.
27.
解:(1)
答:输完这瓶点滴注射液需要180分钟。
(2)设护士给年龄比较大的病人输液速率为,根据题意得
答:输完这瓶点滴注射液的时间将会变为原来的2倍。
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
