浙教版七年级数学上册试题 4.2代数式同步练习(含解析)
文档属性
| 名称 | 浙教版七年级数学上册试题 4.2代数式同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 429.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-10 00:00:00 | ||
图片预览




文档简介
4.2代数式
一、单选题
1.下列代数式书写符合要求的是( )
A. B. C. D.
2.将形如3m和(m,n为正整数)的正整数从小到大排列,并依次记为若第k个数,则k的值为( )
A.682 B.683 C.684 D.685
3.某商品先在批发价m元的基础上提高10%零售,后又降价10%出售,则按后面的售价每销售一件商品的盈亏情况为( ).
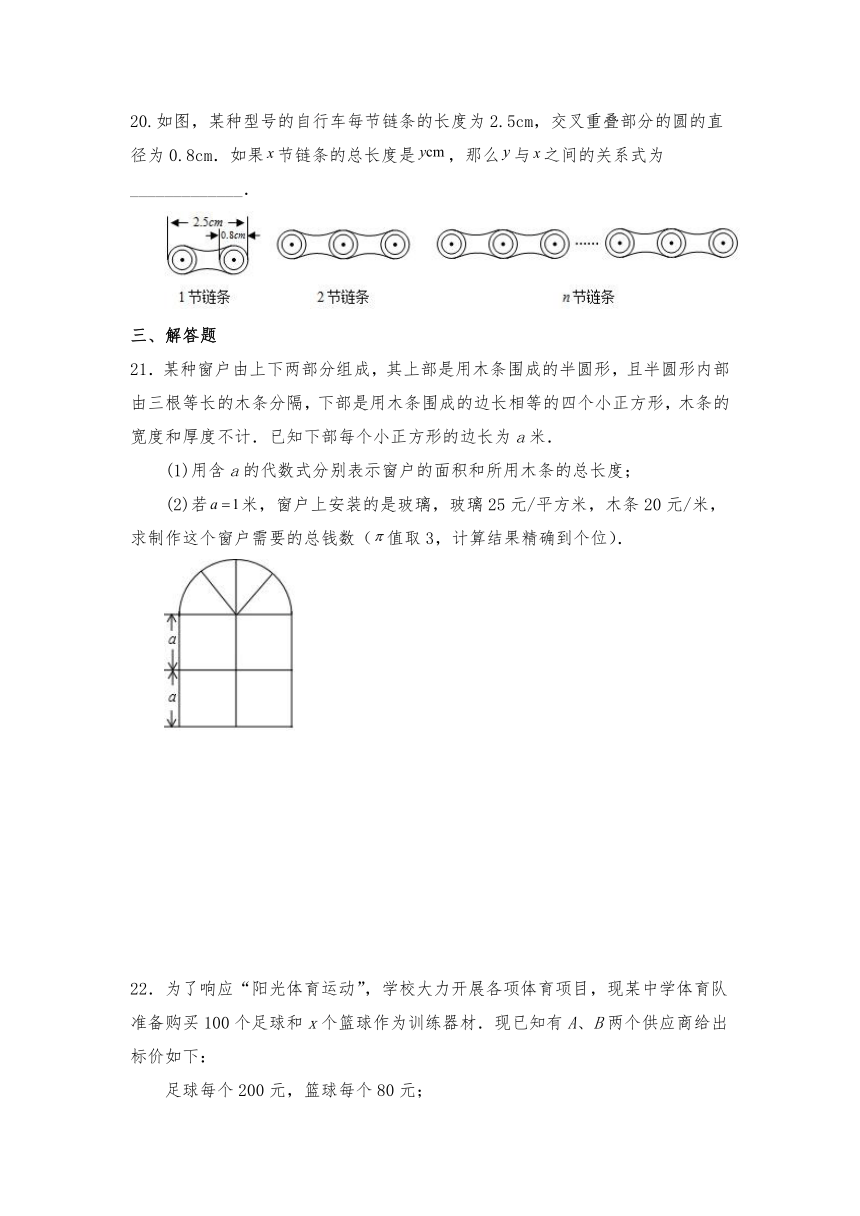
A.亏损了 B.盈利了 C.不亏不盈 D.盈亏不确定
4.粗心的小倩在放学回家后,发现把数学练习册忘在教室了,担心教室关门,于是她跑步到学校取了练习册,再步行回家(取书时间忽略不计).已知跑步速度为x,步行速度为y,则她往返一趟的平均速度是( )
A.x B.y C. D.
5.列式表示“a的3倍与b的相反数的和”,下列正确的是( )
A. B. C. D.
6.(阅读理解)计算:25×11=275,13×11=143,48×11=528,74×11=814,观察算式,我们发现两位乘11的速算方法:头尾一拉,中间相加,满十进一.
[拓展应用]已知一个两位数,十位上的数字是a,个位上的数字是b,这个两位数乘11,计算结果的十位上的数字可表示为( )
A.a或a+1 B.a+b或ab C.a+b 10 D.a+b或a+b 10
7.将全体正偶数排成一个三角形数阵:
按照以上排列的规律,第10行第5个数是( )
A.98 B.100 C.102 D.104
8.对于代数式,第三学习小组讨论后得出如下结论:①代数式还可以写成;②如图,较大正方形的边长为y,较小正方形的边长为1,则代数式表示阴影部分的面积;③其可以叙述为:y与1的平方差的一半;④代数式的值可能是﹣1,其中正确的个数为( )
A.1 B.2 C.3 D.4
9.下列关于代数式“”所表示的意义的说法中正确的是( )
A.与1的和 B.与1的和的相反数
C.与1的差 D.与-1的差的相反数
10.某企业今年一月份投入新产品的研发资金为a万元,以后每月投入新产品的研发资金与上月相比增长率都是20%.该厂今年三月份投入新产品的研发资金为b万元,则( )
A. B. C. D.
二、填空题
11.在,0,,,中,代数式有______个.
12.设n为自然数,则奇数表示为_____,能被5整除的数为_____,被4除余3的数为_____.
13.某书店新进了一批图书,甲、乙两种书的进价分别为4元/本、5元/本.现购进m本甲种书和n本乙种书,共付款Q元.
(1)用含m,n的代数式表示______;
(2)若共购进本甲种书及本乙种书,______(用科学记数法表示).
14.某商店出售一种瓜子,其售价y(元)与瓜子质量x(千克)之间的关系如下表:
质量x(千克) 1 2 3 4 ……
售价y(元) ……
其中售价栏中的0.2是塑料袋的价格.售价y与质量x之间的关系式为______.
15.有一列数按如下规律排列:,,,,,,…,则第2022个数是 _____.
16.围棋是一种起源于中国的棋类游戏,在春秋战国时期即有记载,围棋棋盘由横纵各19条等距线段构成,围棋的棋子分黑白两色,下在横纵线段的交叉点上.若一个白子周围所有相邻(有线段连接)的位置都有黑子,白子就被黑子围住了.如图1,围住1个白子需要4个黑子,固住2个白子需要6个黑子,如图2,围住3个白子需要8个或7个黑子,像这样,不借助棋盘边界,只用15个黑子最多可以围住___个白子.
17.对式子“”,可以这样解释:苹果每千克元,某人买了千克,共付元.请你再对“”给出另一个实际生活方面的合理解释:_____________.
18.两艘船从同一港口出发,甲船顺水而下,乙船逆水而上,已知两船在静水中的速度都是50km/h,水流速度是 km/h. 则2h后两船相距____千米.
19.如图是一所建筑住宅的平面图(图中长度单位:m),用式子表示这块住宅的建筑面积为 _____m2.
20.如图,某种型号的自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.如果节链条的总长度是,那么与之间的关系式为_____________.
三、解答题
21.某种窗户由上下两部分组成,其上部是用木条围成的半圆形,且半圆形内部由三根等长的木条分隔,下部是用木条围成的边长相等的四个小正方形,木条的宽度和厚度不计.已知下部每个小正方形的边长为a米.
(1)用含a的代数式分别表示窗户的面积和所用木条的总长度;
(2)若米,窗户上安装的是玻璃,玻璃25元/平方米,木条20元/米,求制作这个窗户需要的总钱数(值取3,计算结果精确到个位).
22.为了响应“阳光体育运动”,学校大力开展各项体育项目,现某中学体育队准备购买100个足球和x个篮球作为训练器材.现已知有A、B两个供应商给出标价如下:
足球每个200元,篮球每个80元;
供应商A的优惠方案:每买一个足球就赠送一个篮球;
供应商B的优惠方案:足球、篮球均按定价的80%付款.
(1)若,请计算哪种方案划算?
(2),请用含x的代数式,分别把两种方案的费用表示出来.
23.一个服装店的所有服装都打同样的折扣销售.
(1)李阿姨买了一件上衣,原价250元,现价150元,李阿姨还想买一条裤子,原价180元,现价多少钱?
(2)张伯伯有一笔钱,如果买现价90元一件的衬衫,正好买四件,如果想买原价200元一件的夹克衫,能买多少件?
(3)如果用x表示原价,y表示现价y和x关系式是什么?
24.用同样大小的两种不同颜色(白色.灰色)的正方形纸片,按如图方式拼成长方形.
[观察思考]
第(1)个图形中有张正方形纸片;
第(2)个图形中有张正方形纸片;
第(3)个图形中有张正方形纸片;
第(4)个图形中有张正方形纸片;
……
以此类推
(1)[规律总结]第(5)个图形中有__________张正方形纸片(直接写出结果).
(2)根据上面的发现我们可以猜想:__________.(用含n的代数式表示)
(3)[问题解决]根据你的发现计算:.
25.如图,有一个零件,由三部分组成,底座是一个长方体,底面正方形边长为
2Rcm,高为3cm,中间部分是底面半径为Rcm,高为3cm的圆柱,上部是底面半径为rcm,高为2cm的圆柱,计算它的体积.
26.为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的.该市自来水收费的价目表如下(注:水费按月份结算):
每月用水量 价格
不超出5m3的部分 2元/m3
超出5m3不超出10m3的部分 4元/m3
超出10m3的部分 8元/m3
设李老师家某月用水量为.
(1)若,则李老师当月应交水费多少元?
(2)若,则李老师当月应交水费多少元?(用含的代数式表示,并化简)
27.为庆祝北京举办冬季奥运会,甲、乙两校联合准备文艺汇演.甲、乙两校共92人参加演出(其中甲校人数多于乙校人数,且甲校人数不够90人),准备购买统一的演出服装(一人买一套),下面是服装厂给出的演出服装的价格表:
购买服装的套数 1套至45套 46套至90套 91套及以上
每套服装的价格 60元 50元 40元
如果设甲校有学生人参加演出.
(1)若两校联合购买演出服装时,总费用为 元;
(2)若两校各自购买演出服装时,总费用为 元(请用含x的代数式表示).
(3)如果甲校原有60名同学参加演出,
①求两校联合购买演出服装比两校各自独立购买可节省费用多少钱
②如果甲校从参加演出的60名同学中抽调9名同学去参加迎奥运书法比赛不能参加演出,所以甲校只有51人参加演出,那么两校共有哪几种购买演出服装的方案?通过比较,求该如何购买才能使两校购买演出服装的总费用最少?
答案
一、单选题
1.D
【分析】
根据代数式的书写要求:(1)在代数式中出现的乘号,通常简写成“ ”或者省略不写;(2)数字与字母相乘时,数字要写在字母的前面;(3)在代数式中出现的除法运算,一般按照分数的写法来写.带分数要写成假分数的形式.逐一判定即可.
解:A.正确的书写格式是48a;
B.正确的书写格式是;
C.正确的书写格式是;
D. 书写正确.
故选:D.
2.C
【分析】
先确定和不等,考虑在从小到大排列的形如(为正整数)的正整数3,6,9,27,…中,从小到大添加形如(为正整数)的数.再根据即可.
解:易知形如和(,为正整数)的正整数不可能相等.
考虑在从小到大排列的形如(为正整数)的正整数3,6,9,27,…中,从小到大添加形如(为正整数)的数.
由知,将形如(为正整数)的正整数从小到大排列,2022是第674个数.
由于,,所以有10个形如(为正整数)的数小于2022,这10个数排在2022前面.
所以.
3.A
【分析】
原价提高10%后商品新单价为m×(1+10%)元,再按新价降低10%后单价为m×(1+10%)×(1-10%),通过计算即可得到答案.
解:由题意得,后面的售价为:m×(1+10%)×(1-10%)=0.99m元
∵m>0,
∴m>0.99m,
∴按后面的售价每销售一件商品,为亏损情况
故选:A.
4.D
【分析】
设从学校到家路程为s,然后表示出从家到学校所用时间,再表示出从学校到家所用时间,然后利用总路程除以总时间可得平均速度.
解:设从学校到家路程为s,
平均速度是:
;
故选:D.
5.B
【分析】
根据运算的顺序表示即可.
解:a的3倍与b的相反数的和表示为3a-b,
故选B.
6.D
【分析】
根据题目中的速算法可以解答本题.
解:由题意可得,某一个两位数十位数字是a,个位数字是b,将这个两位数乘11,得到一个三位数,
则根据上述的方法可得:当a+b< 10时,该三位数百位数字是a,十位数字是a + b,个位数字是b,
当a+b≥10时,结果的百位数字是a + 1,十位数字是a+b- 10,个位数字是b.
所以计算结果中十位上的数字可表示为:a+b 或a+b 10.
故选:D.
7.B
【分析】
观察数字的变化,第n行有n个偶数,求出第n行第一个数,故可求解.
解:观察数字的变化可知:
第n行有n个偶数,
因为第1行的第1个数是: ;
第2行的第1个数是: ;
第3行的第1个数是:;
…
所以第n行的第1个数是: ,
所以第10行第1个数是:,
所以第10行第5个数是: .
故选:B.
8.C
【分析】
根据代数式的书写方式、代数式与图形、平方差、偶次方的非负性逐个判断即可得.
解:代数式还可以写成,则①正确;
图中阴影部分的面积等于较大正方形的面积与较小正方形的面积之差的一半,即为,则②正确;
代数式可以叙述为:与1的平方差的一半,则③正确;
,
,
所以代数式的值不可能是,即④错误;
综上,正确的个数为3个,
故选:C.
9.A
【分析】
说出代数式的意义,实际上就是把代数式用语言叙述出来.叙述时,要求既要表明运算的顺序,又要说出运算的最终结果.
解:A、x的相反数与1的和的代数式为“-x+1”,故本选项正确;
B、x与1的和的相反数的代数式为“-(x+1)”,故本选项错误;
C、-x与1的差表示为与题干不符,故本选项错误;
D、x与-1的差表示为与题干不符,故本选项错误.
故选:A.
10.D
【分析】
由一月份新产品的研发资金为a元,根据题意可以得到2月份研发资金为a×(1+20%),而三月份在2月份的基础上又增长了20%,那么三月份的研发资金也可以用b表示出来,由此即可得解.
解:∵一月份新产品的研发资金为a元,
2月份起,每月新产品的研发资金与上月相比增长率都是20%,
∴2月份研发资金为a×(1+20%)=1.2a,
∴三月份的研发资金为b=a×(1+20%)×(1+20%)=a(1+20)2=1.44a.
故选:D.
二、填空题
11.3
【分析】
代数式是指把数或表示数的字母用+、-、×、÷连接起来的式子,而对于带有=、>、<等数量关系的式子则不是代数式.
解:是不等式,不是代数式;是方程,不是代数式;
,0,,,是代数式,共3个.
故答案是:3.
12. 或 5n
【分析】
能被2整除的数是偶数,因此偶数通常可以表示为2n,偶数2n的前一位或后一位都是奇数,则奇数可以表示为或;同理,能被5整除的数必含5这个因数;能被4除余3的数,应为4的倍数且加上3.
解:因为偶数中含有2这个因数,则偶数可以表示为2n,偶数2n的前一位或后一位都是奇数,则奇数可以表示为或;能被5整除的数必含5这个因数,则能被5整除的数可表示为5n;能被4除余3的数可表示为4n+3.
故答案为或;5n;4n+3.
13. 4m+5n
【分析】
(1)根据题意列代数式即可;
(2)根据题意列出算式进行化简即可.
解:(1)由题意,得
Q=4m+5n;
(2)Q=4×+5×
=20×+15×
=35×
=.
故答案为:4m+5n,.
14.
【分析】
由题意分析1千克时,售价为:3.6+0.2;2千克时,售价为:2×3.6+0.2;3千克时,售价为:3×3.6+0.2;x千克时,售价为:x×3.6+0.2,即可得到结果.
解:由题意得,时,,
时,,
时,,
时,,
……
因此y与x之间的关系式是.
故答案为:.
15.
【分析】
根据前4个数归纳类推出一般规律,由此即可得.
解:第1个数为,
第2个数为,
第3个数为,
第4个数为,
归纳类推得:第个数为,其中为正整数,
则第2022个数是,
故答案为:.
16.21
【分析】
根据题意可得到黑子的个数为4=4×1,最多可以围住白子的个数为1=2×12-2×1+1,黑子的个数为6=4×2-2,最多可以围住白子的个数为2=2×22-4×2+2;黑子的个数为7=4×2-1,最多可以围住白子的个数为3=2×22-3×2+1;黑子的个数为8=4×2,最多可以围住白子的个数为5=2×22-2×2+1;黑子的个数为9=4×3-3,最多可以围住白子的个数为6=2×32-5×3+3,由此可设黑子的个数为4n-x,其中0≤x≤3,得到当x=0时,最多可以围住白子的个数为2n2-2n+1;当x=1时,最多可以围住白子的个数为2n2-3n+1;当x=2时,最多可以围住白子的个数为2n2-4n+2;当x=3时,最多可以围住白子的个数为2n2-5n+3即可求解.
解:根据题意得:黑子的个数为4=4×1,最多可以围住白子的个数为1=2×12-2×1+1,
黑子的个数为6=4×2-2,最多可以围住白子的个数为2=2×22-4×2+2,
黑子的个数为7=4×2-1,最多可以围住白子的个数为3=2×22-3×2+1,
黑子的个数为8=4×2,最多可以围住白子的个数为5=2×22-2×2+1,
黑子的个数为9=4×3-3,最多可以围住白子的个数为6=2×32-5×3+3,
∴可设黑子的个数为4n-x,其中0≤x≤3,
当x=0时,最多可以围住白子的个数为2n2-2n+1;
当x=1时,最多可以围住白子的个数为2n2-3n+1;
当x=2时,最多可以围住白子的个数为2n2-4n+2;
当x=3时,最多可以围住白子的个数为2n2-5n+3;
∴当黑子的个数为15=4×4-1时,最多可以围住白子的个数为2×42-3×4+1=21个.
故答案为:21
17.一本笔记本3元,买x本,共付3x元
【分析】
对单项式“3x”,是3与x的积,表示生活中的相乘计算.比如:一本笔记本3元,买x本,共付3x元.
解:一本笔记本3元,买x本,共付3x元,答案不唯一.
18.200
【分析】
先表示出甲船顺水速度,乙船逆水速度,再根据路程=速度时间,即可得出结果.
解:∵两船在静水中的速度都是50km/h,水流速度是km/h
∴(50+)km/h,(50)km/h
∵两船背向而行
∴2h后两船距离为:2(50+)+2(50)=200(km)
故答案为:200.
19.(x2+2x+18)
【分析】
根据建筑面积=四个长方形面积的和列代数式,化简即可.
解:面积=x2+2x+3×2+4×3
=x2+2x+6+12
=(x2+2x+18)m2
故答案为:(x2+2x+18).
20.
【分析】
由图形可得算式,总结并确定其链条长度规律,可得答案.
解:由图形可得:
2节链条的长度为:2.5×2-0.8;
3节链条的长度为:2.5×3-0.8×2;
…;
n节链条的总长度为:y=2.5n-0.8(x-1)=1.7x+0.8.
故答案为:y=1.7x+0.8.
三、解答题
21.
解:(1)S=2a×2aπa2=4a2πa2
即窗户的面积为(4a2πa2)米2.
15a+πa=(15+π)a(米)
即制作这种窗户所需材料的总长度(15+π)a(米).
(2)a=1时,25(4a2πa2)+20(15+π)a
≈25×(4×13×1)+20×(15+3)×1
=137.5+360
=497.5
≈498(元),即制作这扇窗户需要498元.
22.
(1)解:当x=100时,供应商A的优惠方案为:(元)
供应商B的优惠方案为:(元)
供应商A的优惠方案划算;
(2)解:当时,供应商A的优惠方案为:(元)
供应商B的优惠方案:(元) .
23.(1)解:计算商品打折数:,
裤子的现价为:(元)
答:现价为元;
(2)解:先求出张伯伯有的钱数:(元),
夹克衫的现价为:(元),
能买夹克衫的件数为:(件)
答:能买3件;
(3)由(1)得,折扣为,
则,
故答案为,
24.
(1)解:第(1)个图形中有2=1×2张正方形纸片;
第(2)个图形中有2(1+2)=6=2×3张正方形纸片;
第(3)个图形中有2(1+2+3)=12=3×4张正方形纸片;
第(4)个图形中有2(1+2+3+4)=20=4×5张正方形纸片;
∴第(5)个图形中有5×6=30张正方形纸片;
故答案为:30;
(2)解:根据(1)的发现猜想:1+2+3+…+n=;
故答案为:;
(3)解:
=(1+2+3++200)-(1+2+3++100)
=-
=20100-5050
=15050.
25.
解:由题意得:体积V=(2R)2×3+πR2×3+πr2×2
=(12R2+3πR2+2πr2)cm3.
答:该几何体的体积是(12R2+3πR2+2πr2)cm3.
26.
解:(1)若李老师家某月用水量为7(m3),则李老师当月应交水费:6×2+1×4=16(元);
所以,李老师当月应交水费16元.
(2)当0<x≤6时,则李老师当月应交水费2x元;
当6<x≤10时,李老师当月应交水费:6×2+(x-6)×4=(4x-12)元,
当10<x<15时,李老师当月应交水费:6×2+4×4+(x-10)×8=(8x-52)元.
综上,若0<x<15,则李老师当月应交水费2x(0<x≤6)元或(4x-12)元(6<x≤10)或(8x-10)元(10<x<15).
27.
解:(1)40×92=3680(元).
故答案为:3680.
(2)设甲校有学生x人参加演出,由题意知45<x<90.
∴50x+60(92-x)=-10x+5520(元).
故答案为:(-10x+5520).
(3)①依题意得:50×60+60×(92-60)-40×92
=3000+1920-3680
=1240(元).
答:两校联合购买演出服装比两校各自独立购买可节省费用1240元.
②方案一:各自购买服装需50×(60-9)+60×(92-60)
=2550+1920
=4470(元);
方案二:联合购买服装需50×(92-9)=4150(元);
方案三:联合购买91套服装需40×91=3640(元);
综上所述:因为4470元>4150元>3640元.
所以应该甲乙两校联合起来选择按40元一次购买91套服装最省钱.
一、单选题
1.下列代数式书写符合要求的是( )
A. B. C. D.
2.将形如3m和(m,n为正整数)的正整数从小到大排列,并依次记为若第k个数,则k的值为( )
A.682 B.683 C.684 D.685
3.某商品先在批发价m元的基础上提高10%零售,后又降价10%出售,则按后面的售价每销售一件商品的盈亏情况为( ).
A.亏损了 B.盈利了 C.不亏不盈 D.盈亏不确定
4.粗心的小倩在放学回家后,发现把数学练习册忘在教室了,担心教室关门,于是她跑步到学校取了练习册,再步行回家(取书时间忽略不计).已知跑步速度为x,步行速度为y,则她往返一趟的平均速度是( )
A.x B.y C. D.
5.列式表示“a的3倍与b的相反数的和”,下列正确的是( )
A. B. C. D.
6.(阅读理解)计算:25×11=275,13×11=143,48×11=528,74×11=814,观察算式,我们发现两位乘11的速算方法:头尾一拉,中间相加,满十进一.
[拓展应用]已知一个两位数,十位上的数字是a,个位上的数字是b,这个两位数乘11,计算结果的十位上的数字可表示为( )
A.a或a+1 B.a+b或ab C.a+b 10 D.a+b或a+b 10
7.将全体正偶数排成一个三角形数阵:
按照以上排列的规律,第10行第5个数是( )
A.98 B.100 C.102 D.104
8.对于代数式,第三学习小组讨论后得出如下结论:①代数式还可以写成;②如图,较大正方形的边长为y,较小正方形的边长为1,则代数式表示阴影部分的面积;③其可以叙述为:y与1的平方差的一半;④代数式的值可能是﹣1,其中正确的个数为( )
A.1 B.2 C.3 D.4
9.下列关于代数式“”所表示的意义的说法中正确的是( )
A.与1的和 B.与1的和的相反数
C.与1的差 D.与-1的差的相反数
10.某企业今年一月份投入新产品的研发资金为a万元,以后每月投入新产品的研发资金与上月相比增长率都是20%.该厂今年三月份投入新产品的研发资金为b万元,则( )
A. B. C. D.
二、填空题
11.在,0,,,中,代数式有______个.
12.设n为自然数,则奇数表示为_____,能被5整除的数为_____,被4除余3的数为_____.
13.某书店新进了一批图书,甲、乙两种书的进价分别为4元/本、5元/本.现购进m本甲种书和n本乙种书,共付款Q元.
(1)用含m,n的代数式表示______;
(2)若共购进本甲种书及本乙种书,______(用科学记数法表示).
14.某商店出售一种瓜子,其售价y(元)与瓜子质量x(千克)之间的关系如下表:
质量x(千克) 1 2 3 4 ……
售价y(元) ……
其中售价栏中的0.2是塑料袋的价格.售价y与质量x之间的关系式为______.
15.有一列数按如下规律排列:,,,,,,…,则第2022个数是 _____.
16.围棋是一种起源于中国的棋类游戏,在春秋战国时期即有记载,围棋棋盘由横纵各19条等距线段构成,围棋的棋子分黑白两色,下在横纵线段的交叉点上.若一个白子周围所有相邻(有线段连接)的位置都有黑子,白子就被黑子围住了.如图1,围住1个白子需要4个黑子,固住2个白子需要6个黑子,如图2,围住3个白子需要8个或7个黑子,像这样,不借助棋盘边界,只用15个黑子最多可以围住___个白子.
17.对式子“”,可以这样解释:苹果每千克元,某人买了千克,共付元.请你再对“”给出另一个实际生活方面的合理解释:_____________.
18.两艘船从同一港口出发,甲船顺水而下,乙船逆水而上,已知两船在静水中的速度都是50km/h,水流速度是 km/h. 则2h后两船相距____千米.
19.如图是一所建筑住宅的平面图(图中长度单位:m),用式子表示这块住宅的建筑面积为 _____m2.
20.如图,某种型号的自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.如果节链条的总长度是,那么与之间的关系式为_____________.
三、解答题
21.某种窗户由上下两部分组成,其上部是用木条围成的半圆形,且半圆形内部由三根等长的木条分隔,下部是用木条围成的边长相等的四个小正方形,木条的宽度和厚度不计.已知下部每个小正方形的边长为a米.
(1)用含a的代数式分别表示窗户的面积和所用木条的总长度;
(2)若米,窗户上安装的是玻璃,玻璃25元/平方米,木条20元/米,求制作这个窗户需要的总钱数(值取3,计算结果精确到个位).
22.为了响应“阳光体育运动”,学校大力开展各项体育项目,现某中学体育队准备购买100个足球和x个篮球作为训练器材.现已知有A、B两个供应商给出标价如下:
足球每个200元,篮球每个80元;
供应商A的优惠方案:每买一个足球就赠送一个篮球;
供应商B的优惠方案:足球、篮球均按定价的80%付款.
(1)若,请计算哪种方案划算?
(2),请用含x的代数式,分别把两种方案的费用表示出来.
23.一个服装店的所有服装都打同样的折扣销售.
(1)李阿姨买了一件上衣,原价250元,现价150元,李阿姨还想买一条裤子,原价180元,现价多少钱?
(2)张伯伯有一笔钱,如果买现价90元一件的衬衫,正好买四件,如果想买原价200元一件的夹克衫,能买多少件?
(3)如果用x表示原价,y表示现价y和x关系式是什么?
24.用同样大小的两种不同颜色(白色.灰色)的正方形纸片,按如图方式拼成长方形.
[观察思考]
第(1)个图形中有张正方形纸片;
第(2)个图形中有张正方形纸片;
第(3)个图形中有张正方形纸片;
第(4)个图形中有张正方形纸片;
……
以此类推
(1)[规律总结]第(5)个图形中有__________张正方形纸片(直接写出结果).
(2)根据上面的发现我们可以猜想:__________.(用含n的代数式表示)
(3)[问题解决]根据你的发现计算:.
25.如图,有一个零件,由三部分组成,底座是一个长方体,底面正方形边长为
2Rcm,高为3cm,中间部分是底面半径为Rcm,高为3cm的圆柱,上部是底面半径为rcm,高为2cm的圆柱,计算它的体积.
26.为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的.该市自来水收费的价目表如下(注:水费按月份结算):
每月用水量 价格
不超出5m3的部分 2元/m3
超出5m3不超出10m3的部分 4元/m3
超出10m3的部分 8元/m3
设李老师家某月用水量为.
(1)若,则李老师当月应交水费多少元?
(2)若,则李老师当月应交水费多少元?(用含的代数式表示,并化简)
27.为庆祝北京举办冬季奥运会,甲、乙两校联合准备文艺汇演.甲、乙两校共92人参加演出(其中甲校人数多于乙校人数,且甲校人数不够90人),准备购买统一的演出服装(一人买一套),下面是服装厂给出的演出服装的价格表:
购买服装的套数 1套至45套 46套至90套 91套及以上
每套服装的价格 60元 50元 40元
如果设甲校有学生人参加演出.
(1)若两校联合购买演出服装时,总费用为 元;
(2)若两校各自购买演出服装时,总费用为 元(请用含x的代数式表示).
(3)如果甲校原有60名同学参加演出,
①求两校联合购买演出服装比两校各自独立购买可节省费用多少钱
②如果甲校从参加演出的60名同学中抽调9名同学去参加迎奥运书法比赛不能参加演出,所以甲校只有51人参加演出,那么两校共有哪几种购买演出服装的方案?通过比较,求该如何购买才能使两校购买演出服装的总费用最少?
答案
一、单选题
1.D
【分析】
根据代数式的书写要求:(1)在代数式中出现的乘号,通常简写成“ ”或者省略不写;(2)数字与字母相乘时,数字要写在字母的前面;(3)在代数式中出现的除法运算,一般按照分数的写法来写.带分数要写成假分数的形式.逐一判定即可.
解:A.正确的书写格式是48a;
B.正确的书写格式是;
C.正确的书写格式是;
D. 书写正确.
故选:D.
2.C
【分析】
先确定和不等,考虑在从小到大排列的形如(为正整数)的正整数3,6,9,27,…中,从小到大添加形如(为正整数)的数.再根据即可.
解:易知形如和(,为正整数)的正整数不可能相等.
考虑在从小到大排列的形如(为正整数)的正整数3,6,9,27,…中,从小到大添加形如(为正整数)的数.
由知,将形如(为正整数)的正整数从小到大排列,2022是第674个数.
由于,,所以有10个形如(为正整数)的数小于2022,这10个数排在2022前面.
所以.
3.A
【分析】
原价提高10%后商品新单价为m×(1+10%)元,再按新价降低10%后单价为m×(1+10%)×(1-10%),通过计算即可得到答案.
解:由题意得,后面的售价为:m×(1+10%)×(1-10%)=0.99m元
∵m>0,
∴m>0.99m,
∴按后面的售价每销售一件商品,为亏损情况
故选:A.
4.D
【分析】
设从学校到家路程为s,然后表示出从家到学校所用时间,再表示出从学校到家所用时间,然后利用总路程除以总时间可得平均速度.
解:设从学校到家路程为s,
平均速度是:
;
故选:D.
5.B
【分析】
根据运算的顺序表示即可.
解:a的3倍与b的相反数的和表示为3a-b,
故选B.
6.D
【分析】
根据题目中的速算法可以解答本题.
解:由题意可得,某一个两位数十位数字是a,个位数字是b,将这个两位数乘11,得到一个三位数,
则根据上述的方法可得:当a+b< 10时,该三位数百位数字是a,十位数字是a + b,个位数字是b,
当a+b≥10时,结果的百位数字是a + 1,十位数字是a+b- 10,个位数字是b.
所以计算结果中十位上的数字可表示为:a+b 或a+b 10.
故选:D.
7.B
【分析】
观察数字的变化,第n行有n个偶数,求出第n行第一个数,故可求解.
解:观察数字的变化可知:
第n行有n个偶数,
因为第1行的第1个数是: ;
第2行的第1个数是: ;
第3行的第1个数是:;
…
所以第n行的第1个数是: ,
所以第10行第1个数是:,
所以第10行第5个数是: .
故选:B.
8.C
【分析】
根据代数式的书写方式、代数式与图形、平方差、偶次方的非负性逐个判断即可得.
解:代数式还可以写成,则①正确;
图中阴影部分的面积等于较大正方形的面积与较小正方形的面积之差的一半,即为,则②正确;
代数式可以叙述为:与1的平方差的一半,则③正确;
,
,
所以代数式的值不可能是,即④错误;
综上,正确的个数为3个,
故选:C.
9.A
【分析】
说出代数式的意义,实际上就是把代数式用语言叙述出来.叙述时,要求既要表明运算的顺序,又要说出运算的最终结果.
解:A、x的相反数与1的和的代数式为“-x+1”,故本选项正确;
B、x与1的和的相反数的代数式为“-(x+1)”,故本选项错误;
C、-x与1的差表示为与题干不符,故本选项错误;
D、x与-1的差表示为与题干不符,故本选项错误.
故选:A.
10.D
【分析】
由一月份新产品的研发资金为a元,根据题意可以得到2月份研发资金为a×(1+20%),而三月份在2月份的基础上又增长了20%,那么三月份的研发资金也可以用b表示出来,由此即可得解.
解:∵一月份新产品的研发资金为a元,
2月份起,每月新产品的研发资金与上月相比增长率都是20%,
∴2月份研发资金为a×(1+20%)=1.2a,
∴三月份的研发资金为b=a×(1+20%)×(1+20%)=a(1+20)2=1.44a.
故选:D.
二、填空题
11.3
【分析】
代数式是指把数或表示数的字母用+、-、×、÷连接起来的式子,而对于带有=、>、<等数量关系的式子则不是代数式.
解:是不等式,不是代数式;是方程,不是代数式;
,0,,,是代数式,共3个.
故答案是:3.
12. 或 5n
【分析】
能被2整除的数是偶数,因此偶数通常可以表示为2n,偶数2n的前一位或后一位都是奇数,则奇数可以表示为或;同理,能被5整除的数必含5这个因数;能被4除余3的数,应为4的倍数且加上3.
解:因为偶数中含有2这个因数,则偶数可以表示为2n,偶数2n的前一位或后一位都是奇数,则奇数可以表示为或;能被5整除的数必含5这个因数,则能被5整除的数可表示为5n;能被4除余3的数可表示为4n+3.
故答案为或;5n;4n+3.
13. 4m+5n
【分析】
(1)根据题意列代数式即可;
(2)根据题意列出算式进行化简即可.
解:(1)由题意,得
Q=4m+5n;
(2)Q=4×+5×
=20×+15×
=35×
=.
故答案为:4m+5n,.
14.
【分析】
由题意分析1千克时,售价为:3.6+0.2;2千克时,售价为:2×3.6+0.2;3千克时,售价为:3×3.6+0.2;x千克时,售价为:x×3.6+0.2,即可得到结果.
解:由题意得,时,,
时,,
时,,
时,,
……
因此y与x之间的关系式是.
故答案为:.
15.
【分析】
根据前4个数归纳类推出一般规律,由此即可得.
解:第1个数为,
第2个数为,
第3个数为,
第4个数为,
归纳类推得:第个数为,其中为正整数,
则第2022个数是,
故答案为:.
16.21
【分析】
根据题意可得到黑子的个数为4=4×1,最多可以围住白子的个数为1=2×12-2×1+1,黑子的个数为6=4×2-2,最多可以围住白子的个数为2=2×22-4×2+2;黑子的个数为7=4×2-1,最多可以围住白子的个数为3=2×22-3×2+1;黑子的个数为8=4×2,最多可以围住白子的个数为5=2×22-2×2+1;黑子的个数为9=4×3-3,最多可以围住白子的个数为6=2×32-5×3+3,由此可设黑子的个数为4n-x,其中0≤x≤3,得到当x=0时,最多可以围住白子的个数为2n2-2n+1;当x=1时,最多可以围住白子的个数为2n2-3n+1;当x=2时,最多可以围住白子的个数为2n2-4n+2;当x=3时,最多可以围住白子的个数为2n2-5n+3即可求解.
解:根据题意得:黑子的个数为4=4×1,最多可以围住白子的个数为1=2×12-2×1+1,
黑子的个数为6=4×2-2,最多可以围住白子的个数为2=2×22-4×2+2,
黑子的个数为7=4×2-1,最多可以围住白子的个数为3=2×22-3×2+1,
黑子的个数为8=4×2,最多可以围住白子的个数为5=2×22-2×2+1,
黑子的个数为9=4×3-3,最多可以围住白子的个数为6=2×32-5×3+3,
∴可设黑子的个数为4n-x,其中0≤x≤3,
当x=0时,最多可以围住白子的个数为2n2-2n+1;
当x=1时,最多可以围住白子的个数为2n2-3n+1;
当x=2时,最多可以围住白子的个数为2n2-4n+2;
当x=3时,最多可以围住白子的个数为2n2-5n+3;
∴当黑子的个数为15=4×4-1时,最多可以围住白子的个数为2×42-3×4+1=21个.
故答案为:21
17.一本笔记本3元,买x本,共付3x元
【分析】
对单项式“3x”,是3与x的积,表示生活中的相乘计算.比如:一本笔记本3元,买x本,共付3x元.
解:一本笔记本3元,买x本,共付3x元,答案不唯一.
18.200
【分析】
先表示出甲船顺水速度,乙船逆水速度,再根据路程=速度时间,即可得出结果.
解:∵两船在静水中的速度都是50km/h,水流速度是km/h
∴(50+)km/h,(50)km/h
∵两船背向而行
∴2h后两船距离为:2(50+)+2(50)=200(km)
故答案为:200.
19.(x2+2x+18)
【分析】
根据建筑面积=四个长方形面积的和列代数式,化简即可.
解:面积=x2+2x+3×2+4×3
=x2+2x+6+12
=(x2+2x+18)m2
故答案为:(x2+2x+18).
20.
【分析】
由图形可得算式,总结并确定其链条长度规律,可得答案.
解:由图形可得:
2节链条的长度为:2.5×2-0.8;
3节链条的长度为:2.5×3-0.8×2;
…;
n节链条的总长度为:y=2.5n-0.8(x-1)=1.7x+0.8.
故答案为:y=1.7x+0.8.
三、解答题
21.
解:(1)S=2a×2aπa2=4a2πa2
即窗户的面积为(4a2πa2)米2.
15a+πa=(15+π)a(米)
即制作这种窗户所需材料的总长度(15+π)a(米).
(2)a=1时,25(4a2πa2)+20(15+π)a
≈25×(4×13×1)+20×(15+3)×1
=137.5+360
=497.5
≈498(元),即制作这扇窗户需要498元.
22.
(1)解:当x=100时,供应商A的优惠方案为:(元)
供应商B的优惠方案为:(元)
供应商A的优惠方案划算;
(2)解:当时,供应商A的优惠方案为:(元)
供应商B的优惠方案:(元) .
23.(1)解:计算商品打折数:,
裤子的现价为:(元)
答:现价为元;
(2)解:先求出张伯伯有的钱数:(元),
夹克衫的现价为:(元),
能买夹克衫的件数为:(件)
答:能买3件;
(3)由(1)得,折扣为,
则,
故答案为,
24.
(1)解:第(1)个图形中有2=1×2张正方形纸片;
第(2)个图形中有2(1+2)=6=2×3张正方形纸片;
第(3)个图形中有2(1+2+3)=12=3×4张正方形纸片;
第(4)个图形中有2(1+2+3+4)=20=4×5张正方形纸片;
∴第(5)个图形中有5×6=30张正方形纸片;
故答案为:30;
(2)解:根据(1)的发现猜想:1+2+3+…+n=;
故答案为:;
(3)解:
=(1+2+3++200)-(1+2+3++100)
=-
=20100-5050
=15050.
25.
解:由题意得:体积V=(2R)2×3+πR2×3+πr2×2
=(12R2+3πR2+2πr2)cm3.
答:该几何体的体积是(12R2+3πR2+2πr2)cm3.
26.
解:(1)若李老师家某月用水量为7(m3),则李老师当月应交水费:6×2+1×4=16(元);
所以,李老师当月应交水费16元.
(2)当0<x≤6时,则李老师当月应交水费2x元;
当6<x≤10时,李老师当月应交水费:6×2+(x-6)×4=(4x-12)元,
当10<x<15时,李老师当月应交水费:6×2+4×4+(x-10)×8=(8x-52)元.
综上,若0<x<15,则李老师当月应交水费2x(0<x≤6)元或(4x-12)元(6<x≤10)或(8x-10)元(10<x<15).
27.
解:(1)40×92=3680(元).
故答案为:3680.
(2)设甲校有学生x人参加演出,由题意知45<x<90.
∴50x+60(92-x)=-10x+5520(元).
故答案为:(-10x+5520).
(3)①依题意得:50×60+60×(92-60)-40×92
=3000+1920-3680
=1240(元).
答:两校联合购买演出服装比两校各自独立购买可节省费用1240元.
②方案一:各自购买服装需50×(60-9)+60×(92-60)
=2550+1920
=4470(元);
方案二:联合购买服装需50×(92-9)=4150(元);
方案三:联合购买91套服装需40×91=3640(元);
综上所述:因为4470元>4150元>3640元.
所以应该甲乙两校联合起来选择按40元一次购买91套服装最省钱.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
