矩形、菱形、正方形复习(浙江省绍兴市)
文档属性
| 名称 | 矩形、菱形、正方形复习(浙江省绍兴市) |

|
|
| 格式 | rar | ||
| 文件大小 | 221.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-07 00:00:00 | ||
图片预览




文档简介
课件16张PPT。矩形、菱形、正方形复习 用4个两条直角边分别为5cm和10cm的全等直角三角形能拼成符合下列要求的图形(全部用上,互不重叠且不留空隙)吗?动手试试看,并与同伴进行交流.
(1)不是正方形的矩形
(2)不是正方形的菱形
(3)正方形动手做一做 几种特殊四边形的常用判定方法1、定义:两组对边分别平行 2、两组对边分别相等
3、一组对边平行且相等 4、对角线互相平分1、定义:有一角是直角的平行四边形
2、三个角是直角的四边形
3、对角线相等的平行四边形1、定义:一组邻边相等的平行四边形
2、四条边都相等的四边形
3、对角线互相垂直的平行四边形1、定义:一组邻边相等且有一个角是直角的平行四边形
2、有一组邻边相等的矩形 3、有一个角是直角的菱形
特殊四边形的性质 回顾与思考对边平行
且相等对边平行
且相等对边平行
四边相等对边平行
四边相等互相平分对角相等
邻角互补四个角都是90°四个角都是90°对角相等
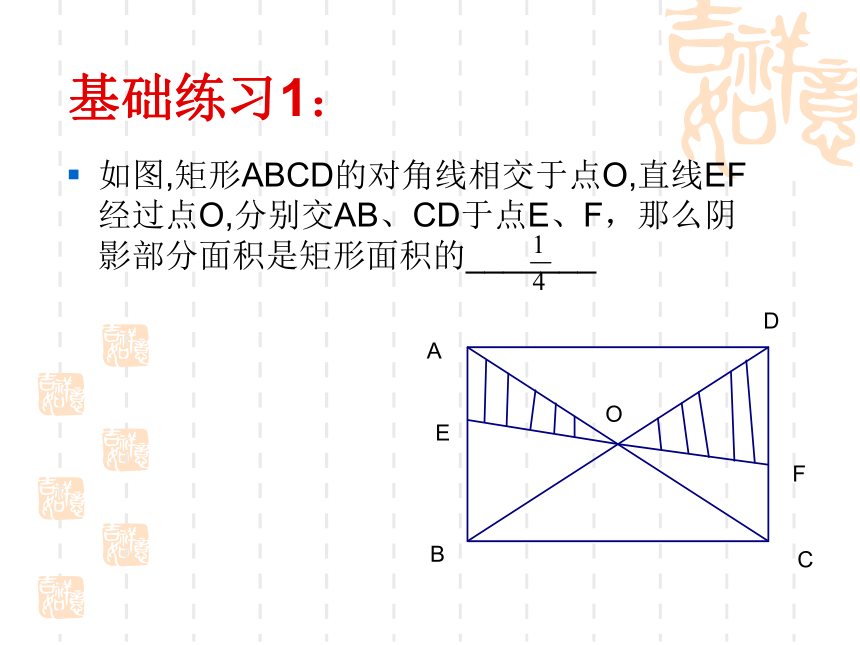
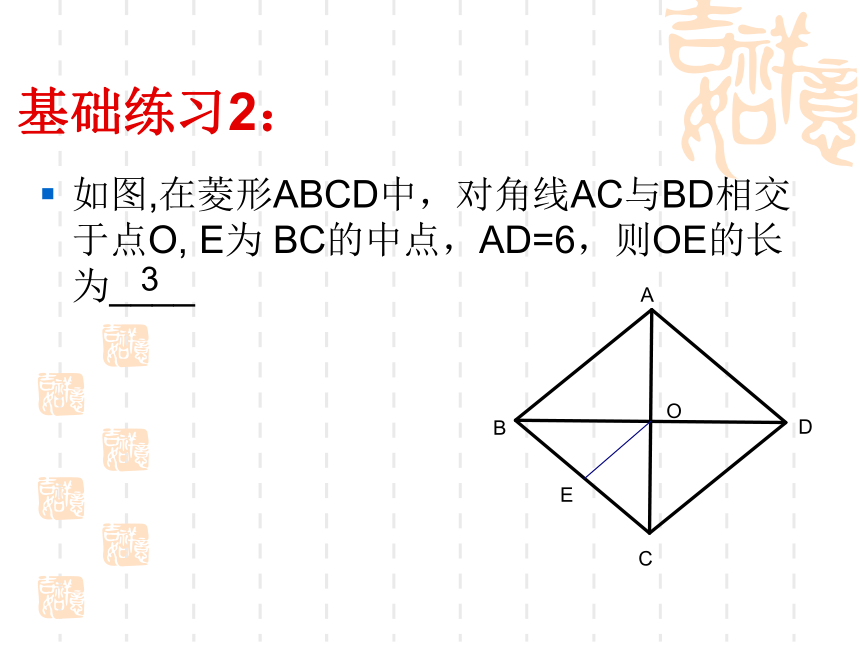
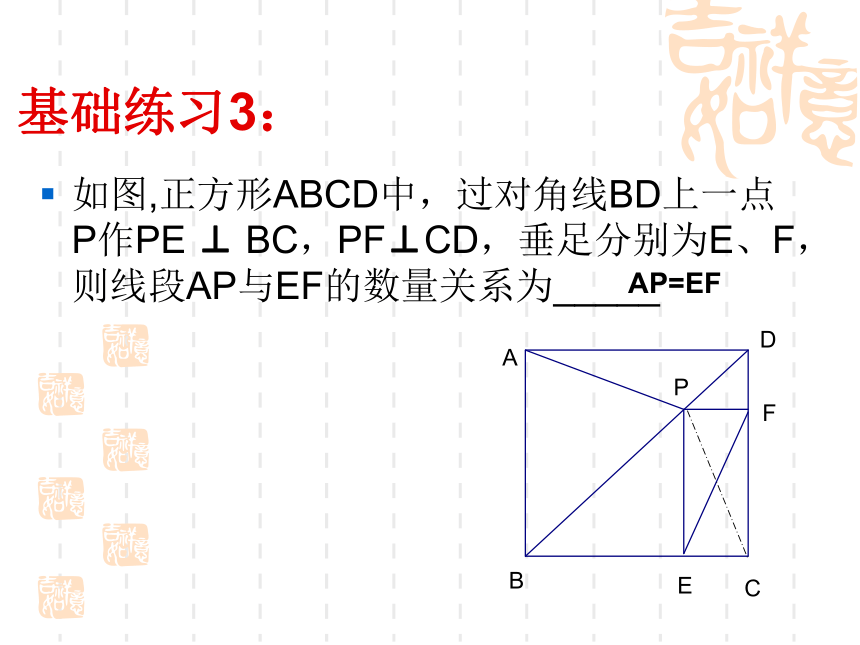
邻角互补互相平分且相等互相平分 且垂直互相平分 垂直且相等基础练习1:如图,矩形ABCD的对角线相交于点O,直线EF经过点O,分别交AB、CD于点E、F,那么阴影部分面积是矩形面积的_______ 基础练习2:如图,在菱形ABCD中,对角线AC与BD相交于点O, E为 BC的中点,AD=6,则OE的长为____ 3基础练习3:如图,正方形ABCD中,过对角线BD上一点P作PE ⊥ BC,PF⊥CD,垂足分别为E、F,则线段AP与EF的数量关系为_____AP=EF
例1、如图矩形纸片ABCD中,现将A、C重合,使纸片折叠压平,设折痕为EF, 回答下列问题:(1) 判断四边形AECF的形状(2) 若AB=3厘米,BC=4厘米,计算重叠部分△AEF的面积应用提高...123例2、在△ABC中, DE ∥AC,DF ∥AB, AD平分∠BAC(1)四边形AEDF是菱形吗?为什么? (2)连结EF交AD于O,若AE=10,
AD=16,求EF (3) △ABC满足什么条件时,
四边形AEDF是正方形,并说明理由。 例3、如图(3),正方形ABCD中,AC、BD相交于O,
MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
1、如图,四边形ABCD四边的 中点分别为E,F,G,H,且AC与BD相等,问:四边形EFGH是怎样的四边形?为什么?合作学习2、如图,四边形ABCD四边的中点分别为E,F,G,H,且AC与BD互相垂直,问:四边形EFGH是怎样的四边形?为什么?合作学习你发现什么特点了吗?下列各类中点四边形的形状分别是:
1、任意四边形的中点四边形是__________
2、平行四边形的中点四边形是____________
3、 矩形的中点四边形是_______________
4、 菱形的中点四边形是___________
5、 正方形的中点四边形是________平行四边形平行四边形菱形矩形正方形合作探究:1、四边形ABCD中,AC=6,BD=8,且AC⊥BD,
顺次连接四边ABCD的中点得到四边形A1B1C1D1,依次类推,得到四边形AnBnCnDn;智慧绽放(1)四边形ABCD中,AC=6,BD=8,且AC⊥BD,
四边形A1B1C1D1是__ _,
四边形A2B2C2D2是___ ,
四边形A11B11C11D11是__ __;矩形矩形菱形你发现了什么规律?(2)四边形ABCD中,AC=6,BD=8,且AC⊥BD,
四边形A1B1C1D1的面积是 ,
四边形A2B2C2D2的面积是 。
四边形AnBnCnDn的面积是 ;126
(1)不是正方形的矩形
(2)不是正方形的菱形
(3)正方形动手做一做 几种特殊四边形的常用判定方法1、定义:两组对边分别平行 2、两组对边分别相等
3、一组对边平行且相等 4、对角线互相平分1、定义:有一角是直角的平行四边形
2、三个角是直角的四边形
3、对角线相等的平行四边形1、定义:一组邻边相等的平行四边形
2、四条边都相等的四边形
3、对角线互相垂直的平行四边形1、定义:一组邻边相等且有一个角是直角的平行四边形
2、有一组邻边相等的矩形 3、有一个角是直角的菱形
特殊四边形的性质 回顾与思考对边平行
且相等对边平行
且相等对边平行
四边相等对边平行
四边相等互相平分对角相等
邻角互补四个角都是90°四个角都是90°对角相等
邻角互补互相平分且相等互相平分 且垂直互相平分 垂直且相等基础练习1:如图,矩形ABCD的对角线相交于点O,直线EF经过点O,分别交AB、CD于点E、F,那么阴影部分面积是矩形面积的_______ 基础练习2:如图,在菱形ABCD中,对角线AC与BD相交于点O, E为 BC的中点,AD=6,则OE的长为____ 3基础练习3:如图,正方形ABCD中,过对角线BD上一点P作PE ⊥ BC,PF⊥CD,垂足分别为E、F,则线段AP与EF的数量关系为_____AP=EF
例1、如图矩形纸片ABCD中,现将A、C重合,使纸片折叠压平,设折痕为EF, 回答下列问题:(1) 判断四边形AECF的形状(2) 若AB=3厘米,BC=4厘米,计算重叠部分△AEF的面积应用提高...123例2、在△ABC中, DE ∥AC,DF ∥AB, AD平分∠BAC(1)四边形AEDF是菱形吗?为什么? (2)连结EF交AD于O,若AE=10,
AD=16,求EF (3) △ABC满足什么条件时,
四边形AEDF是正方形,并说明理由。 例3、如图(3),正方形ABCD中,AC、BD相交于O,
MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
1、如图,四边形ABCD四边的 中点分别为E,F,G,H,且AC与BD相等,问:四边形EFGH是怎样的四边形?为什么?合作学习2、如图,四边形ABCD四边的中点分别为E,F,G,H,且AC与BD互相垂直,问:四边形EFGH是怎样的四边形?为什么?合作学习你发现什么特点了吗?下列各类中点四边形的形状分别是:
1、任意四边形的中点四边形是__________
2、平行四边形的中点四边形是____________
3、 矩形的中点四边形是_______________
4、 菱形的中点四边形是___________
5、 正方形的中点四边形是________平行四边形平行四边形菱形矩形正方形合作探究:1、四边形ABCD中,AC=6,BD=8,且AC⊥BD,
顺次连接四边ABCD的中点得到四边形A1B1C1D1,依次类推,得到四边形AnBnCnDn;智慧绽放(1)四边形ABCD中,AC=6,BD=8,且AC⊥BD,
四边形A1B1C1D1是__ _,
四边形A2B2C2D2是___ ,
四边形A11B11C11D11是__ __;矩形矩形菱形你发现了什么规律?(2)四边形ABCD中,AC=6,BD=8,且AC⊥BD,
四边形A1B1C1D1的面积是 ,
四边形A2B2C2D2的面积是 。
四边形AnBnCnDn的面积是 ;126
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
