浙教版九年级数学下册第1章解直角三角形单元练习题(含解析)
文档属性
| 名称 | 浙教版九年级数学下册第1章解直角三角形单元练习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 622.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-11 10:29:52 | ||
图片预览



文档简介
浙教版九年级数学下册第1章解直角三角形单元练习题
一、单选题
1. 的值等于( )
A.1 B. C. D.
2.在△ABC中,∠C=90°,BC=3,AC=4,则sinA的值是( )
A. B. C. D.
3.如图,已知⊙O的圆心在原点,半径OA=1,设∠AOP=a(a<90°),其始边OA与x轴重合,终边与⊙О相交于点P,设点P的坐标为(x,y),⊙O的切线AT交OP于点T,且AT=m,则下列结论中,错误的是( )
A. B.
C. D.与成反比例
4.在Rt△ABC中,已知∠C=90°,AC=4,BC=3,则cosA等于( )
A. B. C. D.
5.在正方形网格纸中的位置如图(一)所示,则的值是( )
A. B. C. D.
6.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC= ,BC=2,则sin∠ACD的值为( )
A. B. C. D.
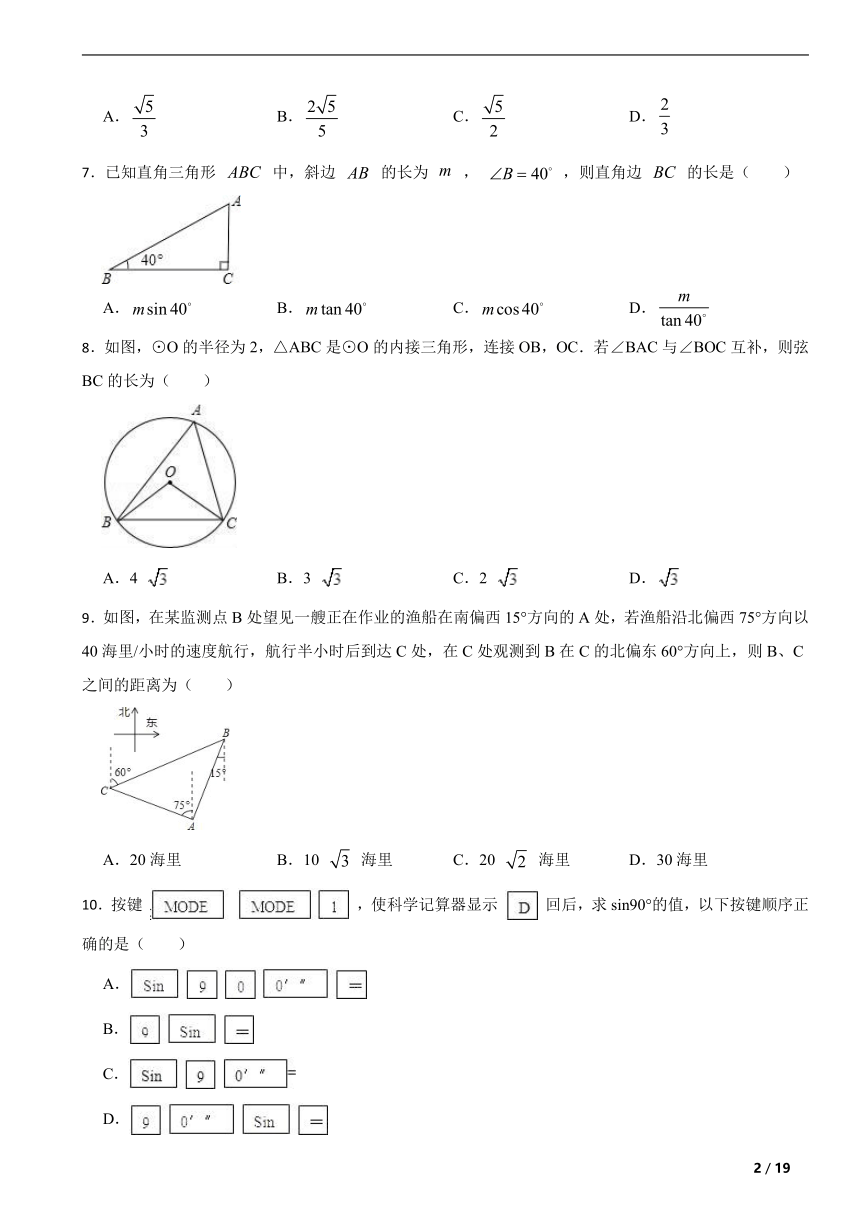
7.已知直角三角形 中,斜边 的长为 , ,则直角边 的长是( )
A. B. C. D.
8.如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连接OB,OC.若∠BAC与∠BOC互补,则弦BC的长为( )
A.4 B.3 C.2 D.
9.如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为( )
A.20海里 B.10 海里 C.20 海里 D.30海里
10.按键 ,使科学记算器显示 回后,求sin90°的值,以下按键顺序正确的是( )
A.
B.
C.
D.
二、填空题
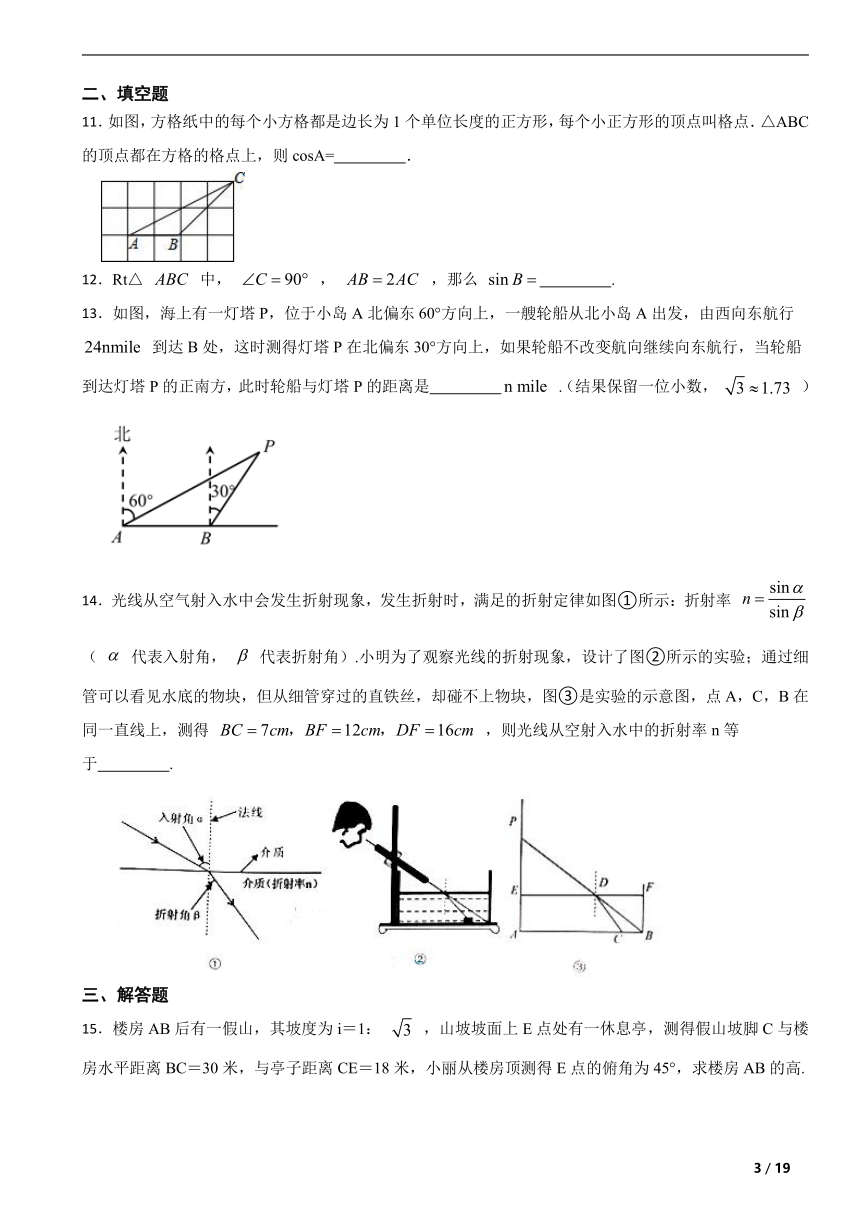
11.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点.△ABC的顶点都在方格的格点上,则cosA= .
12.Rt△ 中, , ,那么 .
13.如图,海上有一灯塔P,位于小岛A北偏东60°方向上,一艘轮船从北小岛A出发,由西向东航行 到达B处,这时测得灯塔P在北偏东30°方向上,如果轮船不改变航向继续向东航行,当轮船到达灯塔P的正南方,此时轮船与灯塔P的距离是 .(结果保留一位小数, )
14.光线从空气射入水中会发生折射现象,发生折射时,满足的折射定律如图①所示:折射率 ( 代表入射角, 代表折射角).小明为了观察光线的折射现象,设计了图②所示的实验;通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块,图③是实验的示意图,点A,C,B在同一直线上,测得 ,则光线从空射入水中的折射率n等于 .
三、解答题
15.楼房AB后有一假山,其坡度为i=1: ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=30米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.
16.如图所示是自动卸货汽车卸货的状态图和其示意图,汽车的车厢采用液压机构,车厢的支撑顶杆AB的底部支撑点B在水平线OP的下方,OB与水平线OP夹角是15°,卸货时车厢与水平线OP成40°,此时OB与支持顶杆AB的夹角为45°,若OA=3米,求AB的长度.(精确到十分位,sin80°≈0.9848,cos80°≈0.1736,tan80°≈5.6712)
17.小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示。于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB。(小平面镜的大小忽略不计)
18.如图,在河对岸有一棵大树A,在河岸B点测得A在北偏东60°方向上,向东前进120m到达C点,测得A在北偏东30°方向上,求河的宽度(精确到0.1m).参考数据: ≈1.414, ≈1.732.
19.如图,在四边形中,,,对角线,交于点,平分,过点作交的延长线于点,连接.
(1)求证:四边形是菱形.
(2)若,,则的值为 .
20.如图, 中, ,点 是边 的中点,以 为底边在其右侧作等腰三角形 ,使 ,连结 ,则:
(1)求证: ;
(2)若 ,求证: .
21.如图①,一台灯放置在水平桌面上,底座AB与桌面垂直,底座高AB=5cm,连杆BC=CD=20cm,BC,CD与AB始终在同一平面内.
(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75)
(1)如图②,转动连杆BC,CD,使∠BCD成平角,∠ABC=143°,求连杆端点D离桌面l的高度DE.
(2)将图②中的连杆CD再绕点C逆时针旋转16°,如图③,此时连杆端点D离桌面l的高度减小了 cm.
22.如图1,某游乐场建造了一个大型摩天轮,工程师介绍:若你站在摩大轮下某处(A点)以的仰角恰好可以看到摩天轮圆轮的底部(C点),可测得的长度为,以的仰角可以看到摩天轮圆轮的最上方(D点),如图2,设摩天轮圆轮的直径垂地面于点B,点A,B在同一水平面上.(人的身高忽略不计,参考数据:,结果精确到个位)
(1)求AB的长;
(2)求摩天轮的圆轮直径(即的长).
23.△ 中, .取 边的中点 ,作 ⊥ 于点 ,取 的中点 ,连接 , 交于点 .
(1)如图1,如果 ,求证: ⊥ 并求 的值;
(2)如图2,如果 ,求证: ⊥ 并用含 的式子表示 .
答案解析部分
1.【答案】D
【解析】【解答】 ,
故答案为:D.
【分析】利用特殊角的锐角三角函数值计算求解即可。
2.【答案】B
【解析】【解答】解:在△ABC中,
∠C=90°,
∵AC=4,BC=3,
∴AB= =5.
∴sinA= ,
故答案为:B.
【分析】先根据勾股定理算出AB,再根据正切定义得出结论。
3.【答案】D
【解析】【解答】解:A、sina=,则 ,A正确;
B、cosa=,则 ,B正确;
C、tana=,则 ,C正确;
D、tana==m,则y=mx,y与x成正比例,D错误.
故答案为:D.
【分析】根据锐角三角函数的定义列出代数式,一 一判断即可.
4.【答案】C
【解析】【解答】解:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AB=5.
∴cosA= .
故答案为:C.
【分析】先利用勾股定理求出AB的长,由cosA=计算即得 .
5.【答案】D
【解析】【解答】解:在Rt△ABC中,AC=4,BC=3,如图所示:
由勾股定理得,BA=,
∴,
故答案为:D
【分析】根据勾股定理解直角三角形可得AB的长,再根据锐角三角函数的定义进行计算即可求解。
6.【答案】A
【解析】【解答】解:在直角△ABC中,根据勾股定理可得:AB .
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,∴∠B=∠ACD,∴sin∠ACD=sin∠B .
故答案为:A.
【分析】利用勾股定理求出AB的长,再利用余角的性质得∠B=∠ACD,根据等角的同名三角函数值相等可得到sin∠ACD=sin∠B,然后利用锐角三角函数的定义求出sin∠ACD的值.
7.【答案】C
【解析】【解答】∵cos40°= ,
∴BC=AB cos40°=mcos40°.
故答案为:C.
【分析】根据题意运用锐减三角函数的定义即可求解。
8.【答案】C
【解析】【解答】如图,作OD⊥BC交BC于点D,
设∠A=x°,则∠BOC=(2x)°,
由题意得:∠A+∠BOC=180°,
∴x+2x=180,
解得:x=60,
∴∠BOC=120°,
∵OD⊥BC,OB=OC,
∴∠BOD=∠COD=60°,BD=CD,
∵sin60°= = = ,
∴BD= ,
∴BC=2 .
故答案为:C.
【分析】如图,作OD⊥BC交BC于点D,根据同弧所对的圆周角等于圆心角的一半,设∠A=x°,则∠BOC=(2x)°,又 ∠BAC与∠BOC互补 ,从而列出方程,求解得出x的值,根据等腰三角形的三线合一得出∠BOD=∠COD=60°,BD=CD,根据正弦函数的定义及特殊锐角三角函数值,由∵sin60°= 即可列出方程,求解得出BD的长,进而根据垂径定理得出BC的长。
9.【答案】C
【解析】【解答】如图,
∵∠ABE=15°,∠DAB=∠ABE,
∴∠DAB=15°,
∴∠CAB=∠CAD+∠DAB=90°.
又∵∠FCB=60°,∠CBE=∠FCB,∠CBA+∠ABE=∠CBE,
∴∠CBA=45°.
∴在直角△ABC中,sin∠ABC= = = ,
∴BC=20 海里.
故答案为:C.
【分析】本题考查了解直角三角形的应用-方向角问题,根据题意易求△ABC是等腰直角三角形,通过解该直角三角形来求BC的长度即可得到答案.
10.【答案】A
【解析】【解答】第一步按sin,第二步90,最后按=,
故选A.
【分析】首先知道用计算器求一个角度的函数值的操作过程,然后作出选择.
11.【答案】
【解析】【解答】如图,
,
由勾股定理得AC=2 ,AD=4,
cosA= ,
故答案为: .
【分析】网格中利用勾股定理可得AC=2 ,AD=4,根据cosA= 计算即可.
12.【答案】
【解析】【解答】解:∵△ABC为直角三角形,且∠C=90°,
∴AB2=AC2+BC2,∵AB=2AC,
∴ = = .
【分析】在直角△ABC中,AB2=AC2+BC2,且AB=2AC,利用勾股定理即可解答.
13.【答案】20.8
【解析】【解答】解:过P作PD⊥AB于D,
∵AB=24,
∵∠PAB=90°-60°=30°,∠PBD=90°-30°=60°,
∴∠BPD=30°,
∴∠APB=30°,即∠PAB=∠APB,
∴AB=BP=24,
在直角△PBD中,PD=BP sin∠PBD=24× = ≈20.8.
故答案为:20.8.
【分析】过P作PD⊥AB于D,根据方位角求出∠PBD、∠PAB和BP的长,然后在在直角△PBD中,利用三角函数的定义求PD即可.
14.【答案】
【解析】【解答】解:如图,过D作GH⊥AB于点H,
在Rt△BDF中,BF=12cm,DF=16cm
∴BD= cm
∵四边形BFDH为矩形,
∴BH=DF=16cm,DH=BF=12cm
又∵BC=7cm
∴CH=BH-BC=9cm
∴CD= cm
∵入射角为∠PDG,sin∠PDG=sin∠BDH=
折射角为∠CDH,sin∠CDH=
∴折射率
故答案为: .
【分析】过D作GH⊥AB于点H,利用勾股定理求出BD和CD,再分别求出入射角∠PDG和折射角∠CDH的正弦值,根据公式可得到折射率.
15.【答案】解:过点E作EF⊥BC的延长线于F,EH⊥AB于点H,
在Rt△CEF中,
∵i= = =tan∠ECF,∴∠ECF=30°,
∴EF= CE=9米,CF=9 米,
∴BH=EF=9米,HE=BF=BC+CF=(30+9 )米,
在Rt△AHE中,∵∠HAE=45°,
∴AH=HE=(30+9 )米,
∴AB=AH+HB=(39+9 )米.
答:楼房AB的高为(39+9 )米.
【解析】【分析】过点E作EF⊥BC的延长线于F,EH⊥AB于点H,在Rt△CEF中,利用坡度的定义可求出∠ECF的度数;利用30°角所对的直角边等于斜边的一半求出EF的长,同时可求出CF的长及HE的长;然后在Rt△AHE中,根据AH=HE,可求出AH的长,根据AB=AH+BH,可求出AB的长.
16.【答案】解:由题意得,∠ABO=45°,∠AOP=40°,∠BOP=15°,OA=3米,
过点O作OM⊥AB于M,
在△AOB中,由内角和定理可得,
∠A=180°-∠ABO-∠AOB
=180°-45°-40°-15°
=80°,
在Rt△AOM中,∠A=80°,OA=3米,
∴OM=OA sin80°≈3×0.9848≈2.95(米),
∴AM=OA cos80°≈3×0.1736≈0.52(米),
在Rt△BOM中,∠ABO=845°,
∴BM=OM=2.95米,
∴AB=AM+BM=2.95+0.52≈3.5(米),
答:AB的长度约为3.5米.
【解析】【分析】过点O作OM⊥AB于M,先求出∠A=80°,再利用解直角三角形的方法求出OM和AM的长,最后利用线段的和差求出AB的长即可。
17.【答案】解:如图,过点C作CH⊥AB于点H,
则CH=BD,BH=CD=0.5,
在Rt△ACH中,∠ACH=45°,
∴AH=CH=BD,
∴AB=AH+BH=BD+0.5,
∵EF⊥FB,AB⊥FB,
∴∠EFG=∠ABG=90°,
由题意,易知∠EGF=∠AGB,
∴△EFG∽△ABG,
∴ ,即 ,
解得:BD=17.5,
∴AB=17.5+0.5=18(m),
∴这棵古树的高AB为18m.
【解析】【分析】 如图,过点C作CH⊥AB于点H, 根据矩形的性质得出 CH=BD,BH=CD=0.5, 根据等腰直角三角形的性质得出 AH=CH=BD, 故 AB=AH+BH=BD+0.5, 进而判断出 △EFG∽△ABG, 根据相似三角形对应边成比例得出 ,根据比例式算出BD的长,从而得出答案。
18.【答案】解:过点A作AD⊥直线BC,垂足为点D,如图所示.
在Rt△ABD中,tan∠BAD= ,
∴BD=AD tan60°= AD;
在Rt△ACD中,tan∠CAD= ,
∴CD=AD tan30°= AD.
∴BC=BD-CD= AD=120,
∴AD=103.9.
∴河的宽度为103.9米
【解析】【分析】 过点A作AD⊥直线BC,垂足为点D,如图所示, 根据正切函数的定义及特殊锐角三角函数值,在Rt△ABD中 ,由 BD=AD tan60° 表示出BD, 在Rt△ACD中 ,由CD=AD tan30°表示出CD,再根据BC=BD-CD列出方程,求解即可。
19.【答案】(1)解:∵,
∴,
∵平分,
∴,
∴,
∴,
∵,
∴,
∵,
∴四边形是平行四边形,
∵,
∴是菱形;
(2)
【解析】【解答】(2)∵四边形是菱形,,
∴,,
在中,,由勾股定理得:,
∵,
∴,
∴,
∴,
∴
故答案为:.
【分析】(1)先证出四边形是平行四边形,再结合AD=AB,即可得到是菱形;
(2)先利用勾股定理求出OA的长,再结合,可得。
20.【答案】(1)证明: ,点 是 中点
(2)证明:过点E作 于点H,
∵
∴
, ,
【解析】【分析】(1) 根据直角三角形斜边上中线的性质可得AD=CD=BD,由等腰三角形的性质可得∠B=∠BAD,结合已知条件∠ADE=∠B可得∠BAD=∠ADE,然后根据平行线的判定定理进行证明;
(2)过点E作EH⊥AD于点H,根据∠B=∠ADE结合cosB的值可得cos∠ADE的值,结合三角函数的概念可得DE=4DH,由等腰三角形的性质可得AE=DE,则AE=2AD,证明△ADE≌△CDE,据此可得结论.
21.【答案】(1)解:作BF⊥DE于点F,则∠BFE=∠BFD=90°,
∵DE⊥l,AB⊥l,
∴∠BEA=∠BAE=90°=∠BFE.
∴四边形ABFE为矩形.
∴EF=AB=5cm,EF∥AB,
∵EF∥AB,
∴∠D+∠ABD=180°,
∵∠ABD=143°,
∴∠D=37°,
在Rt△BDF中,∵∠BFD=90°,
∴ =cosD=cos37°=0.8,
∵DB=DC+BC=20+20=40,
∴DF=40×0.8=32,
∴DE=DF+EF=32+5=37cm,
答:连杆端点D离桌面l的高度DE为37cm;
(2)4
【解析】【解答】解:(2)如图3,作DF⊥l于F,CP⊥DF于P,BG⊥DF于G,CH⊥BG于H.则四边形PCHG是矩形,
∵∠CBH=53°,∠CHB=90°,
∴∠BCH=37°,
∵∠BCD=180°﹣16°=164°,∠DCP=37°,
∴CH=BCsin53°=20×0.8=16(cm),DP=CDsin37°=20×0.6=12(cm),
∴DF=DP+PG+GF=DP+CH+AB=12+16+5=33(cm),
∴下降高度:DE﹣DF=37﹣33=4(cm).
故答案为:4.
【分析】(1)如图2中,作BO⊥DE于O.解直角三角形求出OD即可解决问题.(2)作DF⊥l于F,CP⊥DF于P,BG⊥DF于G,CH⊥BG于H.则四边形PCHG是矩形,求出DF,再求出DF﹣DE即可解决问题.
22.【答案】(1)解:根据题意知,
∵.
答:AB的长约为.
(2)解:根据题意知,
∴.
由(1)知,
∴
∴
∴.
答:摩天轮的圆轮直径约为.
【解析】【分析】(1) 根据题意知, 代入求解即可;
(2) 根据题意知, 得出BC的值, 由(1)知, 得出DB的值,从而得出CD的值。
23.【答案】(1)解:如图1,连接AD,
∵AB=AC,点D是BC的中点,
∴∠ABC=∠C,∠BAD=∠DAC= ∠BAC,AD⊥BC,
∵AD⊥BC,DE⊥AC,
∴∠ADE+∠CDE=90°,∠C+∠CDE=90°,
∴∠ADE=∠C.
又∵∠ADB=∠DEC=90°,
∴△ADB∽△DEC,∴ ,即AD CE=BD DE.
∵点D是BC的中点,点F是DE的中点,
∴BD= BC,DE=2DF,
∴AD CE═ BC 2DF=BC DF,
∴ ,
又∵∠ADE=∠C,
∴△AFD∽△BEC,
∴ ,在Rt△ADB中,
∵∠ABD=90°-∠BAD=90°- ∠BAC,BD= BC,
∴tan∠ABD=tan(90°- ∠BAC)= ,
∴ = tan(90°- ∠BAC).
∵△AFD∽△BEC,
∴∠DAF=∠CBE.
∵∠CBE+∠BOD=90°,∠AOH=∠BOD,
∴∠DAF+∠AOH=∠CBE+∠BOD=90°,
∴∠AHO=180°-90°=90°,即∠AHB=90°
根据以上结论可得:∠AHB=90°, = tan(90°- ×90°)= ;∴AF⊥BE, =
(2)解:如图2,
根据以上结论可得:∠AHB=90°, = tan(90°- α);∴AF⊥BE, = tan(90°- α)
【解析】【分析】(1)由AB=AC,点D是BC的中点,根据三线合一,得到AD⊥BC,由DE⊥AC,根据同角的余角相等,得到∠ADE=∠C;得到△ADB∽△DEC,得到比例,即AD CE=BD DE;由已知得到AD CE=BC DF,又∠ADE=∠C,得到△AFD∽△BEC,得到比例,在Rt△ADB中,根据三角函数定义,得到∠DAF=∠CBE,由三角形内角和定理求出∠AHO=90°,即∠AHB=90°,根据以上结论可得
1 / 1
一、单选题
1. 的值等于( )
A.1 B. C. D.
2.在△ABC中,∠C=90°,BC=3,AC=4,则sinA的值是( )
A. B. C. D.
3.如图,已知⊙O的圆心在原点,半径OA=1,设∠AOP=a(a<90°),其始边OA与x轴重合,终边与⊙О相交于点P,设点P的坐标为(x,y),⊙O的切线AT交OP于点T,且AT=m,则下列结论中,错误的是( )
A. B.
C. D.与成反比例
4.在Rt△ABC中,已知∠C=90°,AC=4,BC=3,则cosA等于( )
A. B. C. D.
5.在正方形网格纸中的位置如图(一)所示,则的值是( )
A. B. C. D.
6.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC= ,BC=2,则sin∠ACD的值为( )
A. B. C. D.
7.已知直角三角形 中,斜边 的长为 , ,则直角边 的长是( )
A. B. C. D.
8.如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连接OB,OC.若∠BAC与∠BOC互补,则弦BC的长为( )
A.4 B.3 C.2 D.
9.如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为( )
A.20海里 B.10 海里 C.20 海里 D.30海里
10.按键 ,使科学记算器显示 回后,求sin90°的值,以下按键顺序正确的是( )
A.
B.
C.
D.
二、填空题
11.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点.△ABC的顶点都在方格的格点上,则cosA= .
12.Rt△ 中, , ,那么 .
13.如图,海上有一灯塔P,位于小岛A北偏东60°方向上,一艘轮船从北小岛A出发,由西向东航行 到达B处,这时测得灯塔P在北偏东30°方向上,如果轮船不改变航向继续向东航行,当轮船到达灯塔P的正南方,此时轮船与灯塔P的距离是 .(结果保留一位小数, )
14.光线从空气射入水中会发生折射现象,发生折射时,满足的折射定律如图①所示:折射率 ( 代表入射角, 代表折射角).小明为了观察光线的折射现象,设计了图②所示的实验;通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块,图③是实验的示意图,点A,C,B在同一直线上,测得 ,则光线从空射入水中的折射率n等于 .
三、解答题
15.楼房AB后有一假山,其坡度为i=1: ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=30米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.
16.如图所示是自动卸货汽车卸货的状态图和其示意图,汽车的车厢采用液压机构,车厢的支撑顶杆AB的底部支撑点B在水平线OP的下方,OB与水平线OP夹角是15°,卸货时车厢与水平线OP成40°,此时OB与支持顶杆AB的夹角为45°,若OA=3米,求AB的长度.(精确到十分位,sin80°≈0.9848,cos80°≈0.1736,tan80°≈5.6712)
17.小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示。于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB。(小平面镜的大小忽略不计)
18.如图,在河对岸有一棵大树A,在河岸B点测得A在北偏东60°方向上,向东前进120m到达C点,测得A在北偏东30°方向上,求河的宽度(精确到0.1m).参考数据: ≈1.414, ≈1.732.
19.如图,在四边形中,,,对角线,交于点,平分,过点作交的延长线于点,连接.
(1)求证:四边形是菱形.
(2)若,,则的值为 .
20.如图, 中, ,点 是边 的中点,以 为底边在其右侧作等腰三角形 ,使 ,连结 ,则:
(1)求证: ;
(2)若 ,求证: .
21.如图①,一台灯放置在水平桌面上,底座AB与桌面垂直,底座高AB=5cm,连杆BC=CD=20cm,BC,CD与AB始终在同一平面内.
(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75)
(1)如图②,转动连杆BC,CD,使∠BCD成平角,∠ABC=143°,求连杆端点D离桌面l的高度DE.
(2)将图②中的连杆CD再绕点C逆时针旋转16°,如图③,此时连杆端点D离桌面l的高度减小了 cm.
22.如图1,某游乐场建造了一个大型摩天轮,工程师介绍:若你站在摩大轮下某处(A点)以的仰角恰好可以看到摩天轮圆轮的底部(C点),可测得的长度为,以的仰角可以看到摩天轮圆轮的最上方(D点),如图2,设摩天轮圆轮的直径垂地面于点B,点A,B在同一水平面上.(人的身高忽略不计,参考数据:,结果精确到个位)
(1)求AB的长;
(2)求摩天轮的圆轮直径(即的长).
23.△ 中, .取 边的中点 ,作 ⊥ 于点 ,取 的中点 ,连接 , 交于点 .
(1)如图1,如果 ,求证: ⊥ 并求 的值;
(2)如图2,如果 ,求证: ⊥ 并用含 的式子表示 .
答案解析部分
1.【答案】D
【解析】【解答】 ,
故答案为:D.
【分析】利用特殊角的锐角三角函数值计算求解即可。
2.【答案】B
【解析】【解答】解:在△ABC中,
∠C=90°,
∵AC=4,BC=3,
∴AB= =5.
∴sinA= ,
故答案为:B.
【分析】先根据勾股定理算出AB,再根据正切定义得出结论。
3.【答案】D
【解析】【解答】解:A、sina=,则 ,A正确;
B、cosa=,则 ,B正确;
C、tana=,则 ,C正确;
D、tana==m,则y=mx,y与x成正比例,D错误.
故答案为:D.
【分析】根据锐角三角函数的定义列出代数式,一 一判断即可.
4.【答案】C
【解析】【解答】解:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AB=5.
∴cosA= .
故答案为:C.
【分析】先利用勾股定理求出AB的长,由cosA=计算即得 .
5.【答案】D
【解析】【解答】解:在Rt△ABC中,AC=4,BC=3,如图所示:
由勾股定理得,BA=,
∴,
故答案为:D
【分析】根据勾股定理解直角三角形可得AB的长,再根据锐角三角函数的定义进行计算即可求解。
6.【答案】A
【解析】【解答】解:在直角△ABC中,根据勾股定理可得:AB .
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,∴∠B=∠ACD,∴sin∠ACD=sin∠B .
故答案为:A.
【分析】利用勾股定理求出AB的长,再利用余角的性质得∠B=∠ACD,根据等角的同名三角函数值相等可得到sin∠ACD=sin∠B,然后利用锐角三角函数的定义求出sin∠ACD的值.
7.【答案】C
【解析】【解答】∵cos40°= ,
∴BC=AB cos40°=mcos40°.
故答案为:C.
【分析】根据题意运用锐减三角函数的定义即可求解。
8.【答案】C
【解析】【解答】如图,作OD⊥BC交BC于点D,
设∠A=x°,则∠BOC=(2x)°,
由题意得:∠A+∠BOC=180°,
∴x+2x=180,
解得:x=60,
∴∠BOC=120°,
∵OD⊥BC,OB=OC,
∴∠BOD=∠COD=60°,BD=CD,
∵sin60°= = = ,
∴BD= ,
∴BC=2 .
故答案为:C.
【分析】如图,作OD⊥BC交BC于点D,根据同弧所对的圆周角等于圆心角的一半,设∠A=x°,则∠BOC=(2x)°,又 ∠BAC与∠BOC互补 ,从而列出方程,求解得出x的值,根据等腰三角形的三线合一得出∠BOD=∠COD=60°,BD=CD,根据正弦函数的定义及特殊锐角三角函数值,由∵sin60°= 即可列出方程,求解得出BD的长,进而根据垂径定理得出BC的长。
9.【答案】C
【解析】【解答】如图,
∵∠ABE=15°,∠DAB=∠ABE,
∴∠DAB=15°,
∴∠CAB=∠CAD+∠DAB=90°.
又∵∠FCB=60°,∠CBE=∠FCB,∠CBA+∠ABE=∠CBE,
∴∠CBA=45°.
∴在直角△ABC中,sin∠ABC= = = ,
∴BC=20 海里.
故答案为:C.
【分析】本题考查了解直角三角形的应用-方向角问题,根据题意易求△ABC是等腰直角三角形,通过解该直角三角形来求BC的长度即可得到答案.
10.【答案】A
【解析】【解答】第一步按sin,第二步90,最后按=,
故选A.
【分析】首先知道用计算器求一个角度的函数值的操作过程,然后作出选择.
11.【答案】
【解析】【解答】如图,
,
由勾股定理得AC=2 ,AD=4,
cosA= ,
故答案为: .
【分析】网格中利用勾股定理可得AC=2 ,AD=4,根据cosA= 计算即可.
12.【答案】
【解析】【解答】解:∵△ABC为直角三角形,且∠C=90°,
∴AB2=AC2+BC2,∵AB=2AC,
∴ = = .
【分析】在直角△ABC中,AB2=AC2+BC2,且AB=2AC,利用勾股定理即可解答.
13.【答案】20.8
【解析】【解答】解:过P作PD⊥AB于D,
∵AB=24,
∵∠PAB=90°-60°=30°,∠PBD=90°-30°=60°,
∴∠BPD=30°,
∴∠APB=30°,即∠PAB=∠APB,
∴AB=BP=24,
在直角△PBD中,PD=BP sin∠PBD=24× = ≈20.8.
故答案为:20.8.
【分析】过P作PD⊥AB于D,根据方位角求出∠PBD、∠PAB和BP的长,然后在在直角△PBD中,利用三角函数的定义求PD即可.
14.【答案】
【解析】【解答】解:如图,过D作GH⊥AB于点H,
在Rt△BDF中,BF=12cm,DF=16cm
∴BD= cm
∵四边形BFDH为矩形,
∴BH=DF=16cm,DH=BF=12cm
又∵BC=7cm
∴CH=BH-BC=9cm
∴CD= cm
∵入射角为∠PDG,sin∠PDG=sin∠BDH=
折射角为∠CDH,sin∠CDH=
∴折射率
故答案为: .
【分析】过D作GH⊥AB于点H,利用勾股定理求出BD和CD,再分别求出入射角∠PDG和折射角∠CDH的正弦值,根据公式可得到折射率.
15.【答案】解:过点E作EF⊥BC的延长线于F,EH⊥AB于点H,
在Rt△CEF中,
∵i= = =tan∠ECF,∴∠ECF=30°,
∴EF= CE=9米,CF=9 米,
∴BH=EF=9米,HE=BF=BC+CF=(30+9 )米,
在Rt△AHE中,∵∠HAE=45°,
∴AH=HE=(30+9 )米,
∴AB=AH+HB=(39+9 )米.
答:楼房AB的高为(39+9 )米.
【解析】【分析】过点E作EF⊥BC的延长线于F,EH⊥AB于点H,在Rt△CEF中,利用坡度的定义可求出∠ECF的度数;利用30°角所对的直角边等于斜边的一半求出EF的长,同时可求出CF的长及HE的长;然后在Rt△AHE中,根据AH=HE,可求出AH的长,根据AB=AH+BH,可求出AB的长.
16.【答案】解:由题意得,∠ABO=45°,∠AOP=40°,∠BOP=15°,OA=3米,
过点O作OM⊥AB于M,
在△AOB中,由内角和定理可得,
∠A=180°-∠ABO-∠AOB
=180°-45°-40°-15°
=80°,
在Rt△AOM中,∠A=80°,OA=3米,
∴OM=OA sin80°≈3×0.9848≈2.95(米),
∴AM=OA cos80°≈3×0.1736≈0.52(米),
在Rt△BOM中,∠ABO=845°,
∴BM=OM=2.95米,
∴AB=AM+BM=2.95+0.52≈3.5(米),
答:AB的长度约为3.5米.
【解析】【分析】过点O作OM⊥AB于M,先求出∠A=80°,再利用解直角三角形的方法求出OM和AM的长,最后利用线段的和差求出AB的长即可。
17.【答案】解:如图,过点C作CH⊥AB于点H,
则CH=BD,BH=CD=0.5,
在Rt△ACH中,∠ACH=45°,
∴AH=CH=BD,
∴AB=AH+BH=BD+0.5,
∵EF⊥FB,AB⊥FB,
∴∠EFG=∠ABG=90°,
由题意,易知∠EGF=∠AGB,
∴△EFG∽△ABG,
∴ ,即 ,
解得:BD=17.5,
∴AB=17.5+0.5=18(m),
∴这棵古树的高AB为18m.
【解析】【分析】 如图,过点C作CH⊥AB于点H, 根据矩形的性质得出 CH=BD,BH=CD=0.5, 根据等腰直角三角形的性质得出 AH=CH=BD, 故 AB=AH+BH=BD+0.5, 进而判断出 △EFG∽△ABG, 根据相似三角形对应边成比例得出 ,根据比例式算出BD的长,从而得出答案。
18.【答案】解:过点A作AD⊥直线BC,垂足为点D,如图所示.
在Rt△ABD中,tan∠BAD= ,
∴BD=AD tan60°= AD;
在Rt△ACD中,tan∠CAD= ,
∴CD=AD tan30°= AD.
∴BC=BD-CD= AD=120,
∴AD=103.9.
∴河的宽度为103.9米
【解析】【分析】 过点A作AD⊥直线BC,垂足为点D,如图所示, 根据正切函数的定义及特殊锐角三角函数值,在Rt△ABD中 ,由 BD=AD tan60° 表示出BD, 在Rt△ACD中 ,由CD=AD tan30°表示出CD,再根据BC=BD-CD列出方程,求解即可。
19.【答案】(1)解:∵,
∴,
∵平分,
∴,
∴,
∴,
∵,
∴,
∵,
∴四边形是平行四边形,
∵,
∴是菱形;
(2)
【解析】【解答】(2)∵四边形是菱形,,
∴,,
在中,,由勾股定理得:,
∵,
∴,
∴,
∴,
∴
故答案为:.
【分析】(1)先证出四边形是平行四边形,再结合AD=AB,即可得到是菱形;
(2)先利用勾股定理求出OA的长,再结合,可得。
20.【答案】(1)证明: ,点 是 中点
(2)证明:过点E作 于点H,
∵
∴
, ,
【解析】【分析】(1) 根据直角三角形斜边上中线的性质可得AD=CD=BD,由等腰三角形的性质可得∠B=∠BAD,结合已知条件∠ADE=∠B可得∠BAD=∠ADE,然后根据平行线的判定定理进行证明;
(2)过点E作EH⊥AD于点H,根据∠B=∠ADE结合cosB的值可得cos∠ADE的值,结合三角函数的概念可得DE=4DH,由等腰三角形的性质可得AE=DE,则AE=2AD,证明△ADE≌△CDE,据此可得结论.
21.【答案】(1)解:作BF⊥DE于点F,则∠BFE=∠BFD=90°,
∵DE⊥l,AB⊥l,
∴∠BEA=∠BAE=90°=∠BFE.
∴四边形ABFE为矩形.
∴EF=AB=5cm,EF∥AB,
∵EF∥AB,
∴∠D+∠ABD=180°,
∵∠ABD=143°,
∴∠D=37°,
在Rt△BDF中,∵∠BFD=90°,
∴ =cosD=cos37°=0.8,
∵DB=DC+BC=20+20=40,
∴DF=40×0.8=32,
∴DE=DF+EF=32+5=37cm,
答:连杆端点D离桌面l的高度DE为37cm;
(2)4
【解析】【解答】解:(2)如图3,作DF⊥l于F,CP⊥DF于P,BG⊥DF于G,CH⊥BG于H.则四边形PCHG是矩形,
∵∠CBH=53°,∠CHB=90°,
∴∠BCH=37°,
∵∠BCD=180°﹣16°=164°,∠DCP=37°,
∴CH=BCsin53°=20×0.8=16(cm),DP=CDsin37°=20×0.6=12(cm),
∴DF=DP+PG+GF=DP+CH+AB=12+16+5=33(cm),
∴下降高度:DE﹣DF=37﹣33=4(cm).
故答案为:4.
【分析】(1)如图2中,作BO⊥DE于O.解直角三角形求出OD即可解决问题.(2)作DF⊥l于F,CP⊥DF于P,BG⊥DF于G,CH⊥BG于H.则四边形PCHG是矩形,求出DF,再求出DF﹣DE即可解决问题.
22.【答案】(1)解:根据题意知,
∵.
答:AB的长约为.
(2)解:根据题意知,
∴.
由(1)知,
∴
∴
∴.
答:摩天轮的圆轮直径约为.
【解析】【分析】(1) 根据题意知, 代入求解即可;
(2) 根据题意知, 得出BC的值, 由(1)知, 得出DB的值,从而得出CD的值。
23.【答案】(1)解:如图1,连接AD,
∵AB=AC,点D是BC的中点,
∴∠ABC=∠C,∠BAD=∠DAC= ∠BAC,AD⊥BC,
∵AD⊥BC,DE⊥AC,
∴∠ADE+∠CDE=90°,∠C+∠CDE=90°,
∴∠ADE=∠C.
又∵∠ADB=∠DEC=90°,
∴△ADB∽△DEC,∴ ,即AD CE=BD DE.
∵点D是BC的中点,点F是DE的中点,
∴BD= BC,DE=2DF,
∴AD CE═ BC 2DF=BC DF,
∴ ,
又∵∠ADE=∠C,
∴△AFD∽△BEC,
∴ ,在Rt△ADB中,
∵∠ABD=90°-∠BAD=90°- ∠BAC,BD= BC,
∴tan∠ABD=tan(90°- ∠BAC)= ,
∴ = tan(90°- ∠BAC).
∵△AFD∽△BEC,
∴∠DAF=∠CBE.
∵∠CBE+∠BOD=90°,∠AOH=∠BOD,
∴∠DAF+∠AOH=∠CBE+∠BOD=90°,
∴∠AHO=180°-90°=90°,即∠AHB=90°
根据以上结论可得:∠AHB=90°, = tan(90°- ×90°)= ;∴AF⊥BE, =
(2)解:如图2,
根据以上结论可得:∠AHB=90°, = tan(90°- α);∴AF⊥BE, = tan(90°- α)
【解析】【分析】(1)由AB=AC,点D是BC的中点,根据三线合一,得到AD⊥BC,由DE⊥AC,根据同角的余角相等,得到∠ADE=∠C;得到△ADB∽△DEC,得到比例,即AD CE=BD DE;由已知得到AD CE=BC DF,又∠ADE=∠C,得到△AFD∽△BEC,得到比例,在Rt△ADB中,根据三角函数定义,得到∠DAF=∠CBE,由三角形内角和定理求出∠AHO=90°,即∠AHB=90°,根据以上结论可得
1 / 1
