浙教版八年级数学下册第5章特殊平行四边形单元练习题(含解析)
文档属性
| 名称 | 浙教版八年级数学下册第5章特殊平行四边形单元练习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 473.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-11 10:32:12 | ||
图片预览




文档简介
浙教版八年级数学下册第5章特殊平行四边形单元练习题
一、单选题
1.下列说法中,错误的是( ).
A.平行四边形的对角线互相平分 B.对角线互相平分的四边形是平行四边形
C.菱形的对角线互相垂直 D.对角线互相垂直的四边形是菱形
2.下列命题正确的是( )
A.一组邻边相等的四边形是菱形 B.对角线互相平分的四边形是菱形
C.对角线互相垂直的四边形是菱形 D.四条边都相等的四边形是菱形
3.菱形的对角线长分别为6和8,它的面积为( )
A.5 B.20 C.24 D.48
4.已知四边形 是平行四边形, , 相交于点O,下列结论错误的是( )
A. ,
B.当 时,四边形 是菱形
C.当 时,四边形 是矩形
D.当 且 时,四边形 是正方形
5.如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=( )
A.2 B.3 C. D.
6.如图,在矩形 中, ,在 上取一点 ,连接 、 ,将 沿 翻折,使点 落在 处,线段 交 于点 ,将 沿 翻折,使点 的对应点 落在线段 上,若点 恰好为 的中点,则线段 的长为( )
A. B. C. D.
7.若一个四边形的两条对角线相等,我们则称这个四边形为对角线四边形.下列图形是对角线四边形的是( )
A.一般四边形 B.平行四边形 C.矩形 D.菱形
8.要判断一个四边形门框是否为矩形,在下面四个拟定方案中,正确的方案是( )
A.测量对角线是否互相平分且垂直 B.测量对角线是否相互平分
C.测量对角线是否互相平分且相等 D.测量对角线是否互相垂直
9.下列判定矩形中,错误的是( )
A.三个角是直角是四边形是矩形 B.一个角是直角的平行四边形是矩形
C.对角线相等的四边形是矩形 D.对角线平分且相等的四边形是矩形
10.矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是( )
A.2 B.4 C.2 D.4
二、填空题
11.如图,在菱形ABCD中,对角线AC与BD相交于点O,且,,于点E,则 .
12.如图,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO= 度.
13.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 .
14.如图,已知正方形的边长为4,M是对角线上的一个动点(不与B,D重合),连接,过M分别作的垂线段垂足分别为E,F,则的最小值是 .
三、解答题
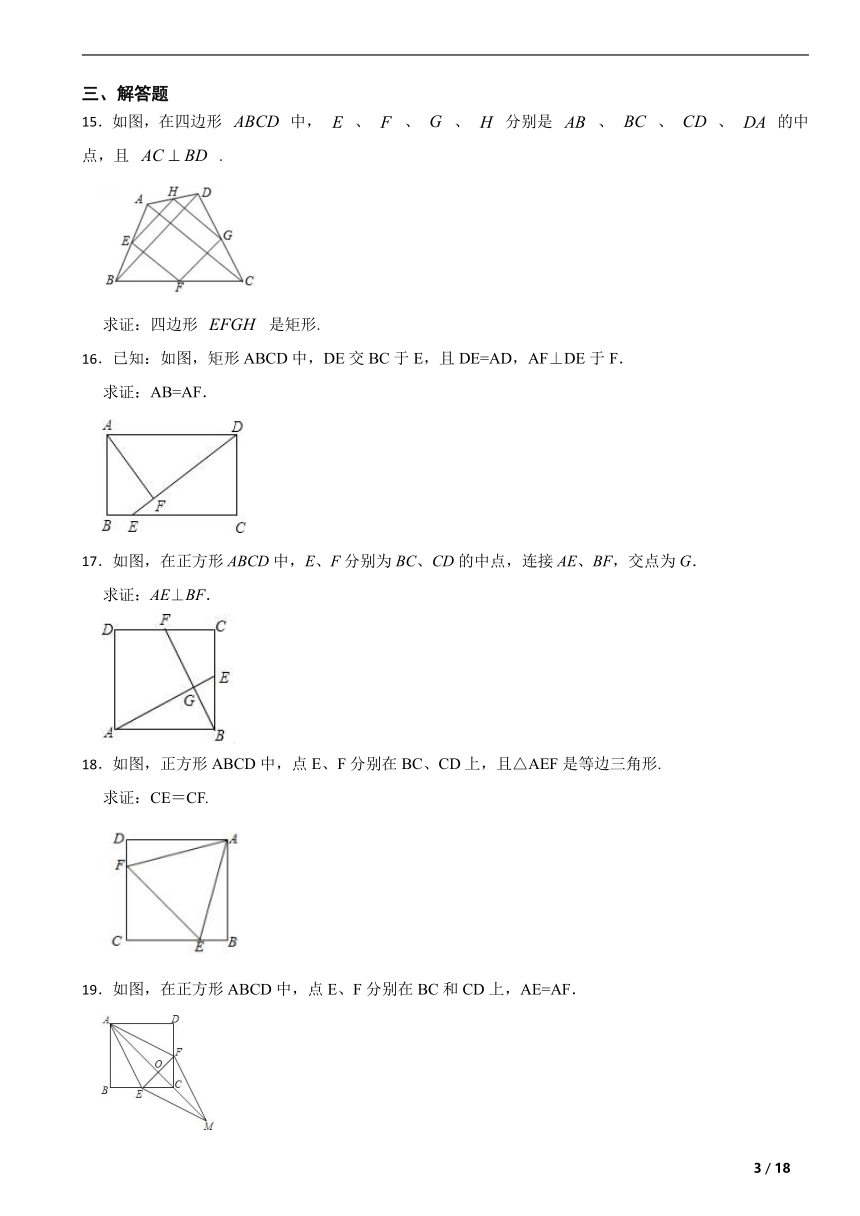
15.如图,在四边形 中, 、 、 、 分别是 、 、 、 的中点,且 .
求证:四边形 是矩形.
16.已知:如图,矩形ABCD中,DE交BC于E,且DE=AD,AF⊥DE于F.
求证:AB=AF.
17.如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
求证:AE⊥BF.
18.如图,正方形ABCD中,点E、F分别在BC、CD上,且△AEF是等边三角形.
求证:CE=CF.
19.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)试说明∠BAE=∠DAF;
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形,并说明你的理由.
20.如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
21.如图,在平行四边形中,边的垂直平分线交于点E,交的延长线于点F,连接,.
(1)求证:;
(2)求证:四边形是菱形.
22.已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
23.问题提出
(1)如图①,在Rt△ABC中,∠A=90°,AB=3,AC=4,在BC上找一点D,使得AD将△ABC分成面积相等的两部分,作出线段AD,并求出AD的长度;
问题探究
(2)如图②,点A、B在直线a上,点M、N在直线b上,且a∥b,连接AN、BM交于点O,连接AM、BN,试判断△AOM与△BON的面积关系,并说明你的理由;
解决问题
(3)如图③,刘老伯有一个形状为筝形OACB的养鸡场,在平面直角坐标系中,O(0,0)、A(4,0)、B(0,4)、C(6,6),是否在边AC上存在一点P,使得过B、P两点修一道笔直的墙(墙的宽度不计),将这个养鸡场分成面积相等的两部分?若存在,请求出直线BP的表达式;若不存在,请说明理由.
答案解析部分
1.【答案】D
【解析】【解答】根据平行四边形和菱形的性质得到A、B、C均正确,而D不正确,因为对角线互相垂直的四边形也可能是梯形,故选D.
【分析】主要考查了平行四边形和特殊平行四边形的特性,并利用性质解题.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.菱形的特性是:四边相等,对角线互相垂直平分.
2.【答案】D
【解析】【解答】解:据“一组邻边相等的平行四边形是菱形”, A选项少平行故不符合题意;
据“对角线互相平分且垂直的四边形是菱形”, B选项少对角线垂直故不符合题意;
据“对角线互相垂直的平行四边形是菱形”, C选项少平行不符合题意;
据“四条边都相等的四边形是菱形”,D选项与菱形的判定定理相同故符合题意;
故答案为:D.
【分析】根据菱形的定义和判定定理进行分析即可。
3.【答案】C
【解析】【解答】解:由题意可得:
故答案为:C
【分析】根据菱形的面积公式即可求出答案。
4.【答案】B
【解析】【解答】解: 四边形 是平行四边形,
,故A正确,
四边形 是平行四边形, ,
不能推出四边形 是菱形,故 错误,
四边形 是平行四边形, ,
四边形 是矩形,故C正确,
四边形 是平行四边形, , ,
四边形 是正方形.故D正确.
故答案为:B.
【分析】(1)根据平行四边形的对角线互相平分可得OA=OC,OB=OD;
(2)根据菱形的判定“一组邻边相等的平行四边形是菱形”可知当AB=CD时,四边形ABCD是菱形错误;
(3)根据一个角是直角的平行四边形是矩形可知 当∠ABC=90°时,四边形 是矩形;
(4)根据对角线相等且互相垂直的平行四边形是正方形可知,当 且 时,四边形 是正方形.
5.【答案】C
【解析】【解答】解:过B点作BF⊥CD,与DC的延长线交于F点,
则有△BCF≌△BAE(ASA),
则BE=BF,S四边形ABCD=S正方形BEDF=8,
∴BE= .
故答案为:C.
【分析】过B点作BF⊥CD,与DC的延长线交于F点,根据全等三角形的判定方法很容易利用ASA判断出△BCF≌△BAE,根据全等三角形的性质得出BE=BF,S△BCF=S△BAE,四边形BEDF是正方形,最后根据S四边形ABCD=S正方形BEDF即可列出方程,求解即可.
6.【答案】D
【解析】【解答】解:设 F长为
∵ 沿 翻折,点 落在 处, 沿 翻折,使点 的对应点 落在线段 上
∴A =AB=CD= D,
由全等三角形判定定理AAS可得
∴ F= ,
∵点 为 的中点
∴
得
故答案为:D。
【分析】设 F长为 ,根据图形沿着某条边折叠所得的两个图形全等,即可推出全等三角形对应的边和角相等,利用得出的结论,再推出 ,F是AD的中点,已知AB=1,再根据边之间的长度关系列出等式,∴ ,得 , .
7.【答案】C
【解析】【解答】解:在一般四边形、平行四边形、矩形、菱形中,只有矩形的对角线相等.故选:C.
【分析】根据矩形的对角线相等,即可解答.
8.【答案】C
【解析】【解答】A、对角线互相平分得到该四边形是平行四边形,而对角线互相垂直的平行四边形是菱形,故A不符合题意;
B、对角线互相平分得到该四边形是平行四边形,故B不符合题意;
C、对角线互相平分得到该四边形是平行四边形,对角线相等的平行四边形是矩形,故C符合题意;
D、对角线是否互相垂直无法判定是何特殊四边形,故D不符合题意.
故答案为:C
【分析】根据平行四边形的判定与性质、矩形的判定、菱形的判定,分别对各个选项进行判断即可。
9.【答案】C
【解析】【解答】解:A:三个角是直角的四边形是矩形正确,不符合题意;
B: 一个角是直角的平行四边形是矩形正确,不符合题意;
C:对角线相等的平行四边形是矩形 ,这里是四边形,所以错误,符合题意;
D:对角线平分且相等的四边形是矩形正确,不符合题意。
故答案为:C。
【分析】分别根据矩形的判定,判断各选项能不能得出矩形的结论,选择错误的选项即可。
10.【答案】B
【解析】【解答】解:如图,
∵矩形ABCD,
∴OA=OB,AC=2OA,
∵∠AOB=60°,
∴△ABO是等边三角形,
∴AO=AB=2,
∴AC=2×2=4.
故答案为:B
【分析】利用矩形的性质可证得OA=OB,AC=2OA,利用有一个角是60°的等腰三角形是等边三角形,可证得△ABO是等边三角形,可求出OA的长,然后求出AC的长.
11.【答案】
【解析】【解答】解:∵ 四边形ABCD是菱形,AC=6,BD=8,
∴AC⊥BD,,,
在中,根据勾股定理得,,
∵S菱形ABCD =AC×BD=BC×AE,
即S菱形ABCD =×6×8=5×AE,
∴AE=.
故答案为:.
【分析】根据菱形的性质:对角线互相垂直平分,可求得OB,OC的值,再根据勾股定理求得菱形的边长,最后再根据菱形的面积获得等式,进而求出高AE的值.
12.【答案】25
【解析】【解答】解:∵四边形ABCD是菱形,
∴OD=OB,∠COD=90°,
∵DH⊥AB,
∴OH=BD=OB,
∴∠OHB=∠OBH,
又∵AB∥CD,
∴∠OBH=∠ODC,
在Rt△COD中,∠ODC+∠DCO=90°,
在Rt△DHB中,∠DHO+∠OHB=90°,
∴∠DHO=∠DCO==25°,
故答案为:25.
【分析】根据菱形的对角线互相平分可得OD=OB,再根据直角三角形斜边上的中线等于斜边的一半可得OH=OB,然后根据等边对等角求出∠OHB=∠OBH,根据两直线平行,内错角相等求出∠OBH=∠ODC,然后根据等角的余角相等解答即可.
13.【答案】
【解析】【解答】解:如图,连接AC、CF,
∵正方形ABCD和正方形CEFG中,BC=1,CE=3,
∴AC= ,CF=3 , ∠ACD=∠GCF=45°,
∴∠ACF=90°,
由勾股定理得,AF= ,
∵H是AF的中点,
∴CH= AF= ×2 = .
故答案为: .
【分析】连接AC、CF,根据正方形形状得出AC、CF,∠ACD=∠GCF=45°,再求出∠ACF=90°,在利用勾股定理列式求出AF,再根据直角三角形些边上的中线等于斜边的一半解答即可。
14.【答案】
【解析】【解答】解:如图:延长FM交CD于P,连结AC交BD于O,
∵四边形为正方形,
∴BD平分又,则
∵BD平分所以易证得:四边形AFPD为矩形,则FP=AD,故
则当时,MC有最小值:故 的最小值是
故答案为:.
【分析】本题主要考查正方形的性质、角平分线的性质、点到直线的距离最小值为垂线段,延长FM交CD于P,连结AC交BD于O,根据正方形及角平分线的性质可得:从而得到:再根据点到直线的距离最小值为垂线段即可求解.
15.【答案】证明:∵点E、F、G、H分别是边AB、BC、CD、DA的中点,
∴EF= AC,GH= AC,
∴EF=GH,同理EH=FG
∴四边形EFGH是平行四边形;
又∵对角线AC、BD互相垂直,
∴EF与FG垂直.
∴四边形EFGH是矩形.
【解析】【分析】根据题意易证得 四边形EFGH是平行四边形,对角线AC、BD互相垂直, 可判定出 四边形EFGH是矩形.
16.【答案】证明:∵AF⊥DE.
∴∠AFE=90°.
∵在矩形ABCD中,AD∥BC,∠C=90°.
∴∠ADF=∠DEC.
∴∠AFE=∠C=90°.
∵AD=DE.
∴△ADF≌△DEC.
∴AF=DC.
∵DC=AB.
∴AF=AB
【解析】【分析】根据已知及矩形的性质利用AAS判定△ADF≌△DEC,从而得到AF=DC,因为DC=AB,所以AF=AB.
17.【答案】证明:∵E,F分别是正方形ABCD边BC,CD的中点, ∴CF=BE, 在Rt△ABE和Rt△BCF中, ∵ , ∴Rt△ABE≌Rt△BCF(SAS), ∴∠BAE=∠CBF, 又∵∠BAE+∠BEA=90°, ∴∠CBF+∠BEA=90°, ∴∠BGE=90°, ∴AE⊥BF.
【解析】【分析】由E,F分别是正方形ABCD边BC,CD的中点知CF=BE,证Rt△ABE≌Rt△BCF得∠BAE=∠CBF,根据∠BAE+∠BEA=90°即可得∠CBF+∠BEA=90°,据此即可得证.
18.【答案】证明:∵四边形ABCD是正方形,
∴AD=AB,∠D=∠B=90°,
∵△AEF是等边三角形,
∴AF=AE,
在Rt△ADF和Rt△ABE中,
,
∴Rt△ADF≌Rt△ABE(HL),
∴DF=BE,
∴CE=CF.
【解析】【分析】利用正方形的性质可得到 AD=AB,∠D=∠B=90°;再利用等边三角形的性质可得到AF=AE;再利用HL证明Rt△ADF≌Rt△ABE,利用全等三角形的对应边相等,可推出DF=BE,由此可证得结论.
19.【答案】(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
在Rt△ABE和Rt△ADF中,
∵ ,
∴Rt△ADF≌Rt△ABE(HL)
∴∠BAE=∠DAF;
(2)解:四边形AEMF是菱形,理由为:
证明:∵四边形ABCD是正方形,
∴∠BCA=∠DCA=45°(正方形的对角线平分一组对角),
BC=DC(正方形四条边相等),
∵BE=DF(已证),
∴BC﹣BE=DC﹣DF(等式的性质),
即CE=CF,
在△COE和△COF中,
,
∴△COE≌△COF(SAS),
∴OE=OF,又OM=OA,
∴四边形AEMF是平行四边形(对角线互相平分的四边形是平行四边形),
∵AE=AF,
∴平行四边形AEMF是菱形.
【解析】【分析】(1)求简单的角相等,可证两角所在的三角形全等,即证△ABE≌△ADF;(2)由于四边形ABCD是正方形,易得∠ECO=∠FCO=45°,BC=CD;联立(1)的结论,可证得EC=CF,根据等腰三角形三线合一的性质可证得OC(即AM)垂直平分EF;已知OA=OM,则EF、AM互相平分,再根据一组邻边相等的平行四边形是菱形,即可判定四边形AEMF是菱形.
20.【答案】(1)证明:∵ 四边形ABCD是平行四边形,
∴ CF∥ED,
∴ ∠FCG=∠EDG,
∵ G是CD的中点,
∴ CG=DG,
在△FCG和△EDG中, ,
∴ △FCG ≌△EDG(ASA),
∴ FG=EG,∵ CG=DG,
∴ 四边形CEDF是平行四边形
(2)3.5;2
【解析】【解答】解:(2)①当AE=3.5时,平行四边形CEDF是矩形,
理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=3,
∴BM=1.5,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5,
∵AE=3.5,
∴DE=1.5=BM,
在△MBA和△EDC中,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
故答案为:3.5;
②当AE=2时,四边形CEDF是菱形,
理由是:∵AD=5,AE=2
,
∴DE=3,
∵CD=3,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
∵四边形CEDF是平行四边形,
∴四边形CEDF是菱形,
故答案为:2
① 当AE=3.5cm时,四边形CEDF是矩形.
② 当AE=2cm时,四边形CEDF是菱形.
【分析】(1)根据“ASA”可证△FCG ≌△EDG,可得FG=EG,根据平行四边形的判定方法即可推出;
(2)①过A作AM⊥BC于M,根据“SAS”可证△MBA≌△EDC,可得∠CED=∠AMB=90°,根据矩形的判定推出即可;
②先求出△CDE是等边三角形,可得CE=DE,利用一组邻边相等的平行四边形是菱形即证.
21.【答案】(1)证明:四边形是平行四边形,
,
,
垂直平分,
,
在和中,
,
;
(2)证明:,
,
,
四边形是平行四边形,
又,
平行四边形是菱形.
【解析】【分析】(1)由平行四边形的小组可得AD∥BC,由平行线的性质可得∠AEG=∠BFG,由线段垂直平分线的性质可得AG=BG,用角角边可证;
(2)由(1)中的全等三角形的性质可得AE=BF,根据一组对边平行且相等的四边形是平行四边形可得四边形AFBE是平行四边形,结合已知根据对角线互相垂直的平行四边形是菱形可得平行四边形AFBE是菱形.
22.【答案】(1)证明:∵四边形ABCD是矩形,∴∠A=∠D=90°,AB=DC,∵M是AD的中点,
∴AM=DM,
在△ABM和△DCM中, ,
∴△ABM≌△DCM(SAS);
(2)解:四边形MENF是菱形;理由如下:由(1)得:△ABM≌△DCM,
∴BM=CM,
∵E、F分别是线段BM、CM的中点,
∴ME=BE= BM,MF=CF= CM,
∴ME=MF,
又∵N是BC的中点,∴EN、FN是△BCM的中位线,∴EN= CM,FN= BM,
∴EN=FN=ME=MF,
∴四边形MENF是菱形.
【解析】【分析】(1)M是边AD的中点,得到AM=DM,根据矩形的性质,得到∠A=∠D,AB=DC,由SAS得到△ABM≌△DCM;(2)由(1)知△ABM≌△DCM,得到对应边BM=CM,由E、F分别是线段BM、CM的中点,得到ME=MF,再根据三角形中位线定理,得到EN=FN=ME=MF,得到四边形MENF是菱形.
23.【答案】(1)解:如图①,取BC边的中点D,连接AD,则线段AD即为所求.
在Rt△ABC中,∠BAC=90°,AB=3,AC=4,
∴BC=,
∵点D为BC的中点,
∴AD=BC=.
(2)解:S△AOM=S△BON,理由如下:
由图可知,S△AOM=S△ABM﹣S△AOB,S△BON=S△ABN﹣S△AOB,
如图②,过点M作MD⊥AB于点D,过点N作NE⊥AB于点E,
∴MD∥NE,∠MDE=90°,
又∵MN∥DE,
∴四边形MDEN是矩形,
∴MD=NE,
∵S△ABM=,S△ABN=,
∴S△ABM=S△ABN,
∴S△AOM=S△BON.
(3)解:存在,直线BP的表达式为:y=x+4.
如图③,连接AB,过点O作OF∥AB,交CA的延长线于点F,连接BF,交OA于点G,
由(2)的结论可知,S△OBG=S△AFG,
∴S四边形OACB=S△BCF,
取CF的中点P,作直线BP,直线BP即为所求.
∵A(4,0),B(0,4),C(6,6),
∴线段AB所在直线表达式为:y=﹣x+4,
线段AC所在直线的表达式为:y=3x﹣12,
∵OF∥AB,且直线OF过原点,
∴直线OF的表达式为:y=﹣x,
联立,解得,
∴F(3,﹣3),
∵点P是CF的中点,
∴P,
∴直线BP的表达式为:y=x+4.
【解析】【分析】(1)利用三角形的中线分得的两个三角形的面积相等,可知取BC边的中点D,连接AD即可;利用勾股定理求出BC的长,再利用直角三角形斜边上的中线等于斜边的一半可得AD的长;
(2)观察图形可知S△AOM=S△ABM﹣S△AOB,S△BON=S△ABN﹣S△AOB,利用利用平行线间的距离处处相等及同底等高的两个三角形的面积相等,可证得△ABM的面积=△ABN的面积,由此可证得结论;
(3)连接AB,过点O作OF∥AB,交CA的延长线于点F,连接BF,交OA于点G,由(2)的结论可证得 S四边形OACB=S△BCF,取CF的中点P,作直线BP,直线BP即为所求;利用待定系数法求出直线AB,AC的函数解析式,利用OF∥AB,可得到直线OF的函数解析式,将直线OF和直线AC联立方程组,解方程组,可得到点F的坐标,利用线段中点坐标可求出点P的坐标,然后利用待定系数法求出直线BP的函数解析式.
1 / 1
一、单选题
1.下列说法中,错误的是( ).
A.平行四边形的对角线互相平分 B.对角线互相平分的四边形是平行四边形
C.菱形的对角线互相垂直 D.对角线互相垂直的四边形是菱形
2.下列命题正确的是( )
A.一组邻边相等的四边形是菱形 B.对角线互相平分的四边形是菱形
C.对角线互相垂直的四边形是菱形 D.四条边都相等的四边形是菱形
3.菱形的对角线长分别为6和8,它的面积为( )
A.5 B.20 C.24 D.48
4.已知四边形 是平行四边形, , 相交于点O,下列结论错误的是( )
A. ,
B.当 时,四边形 是菱形
C.当 时,四边形 是矩形
D.当 且 时,四边形 是正方形
5.如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=( )
A.2 B.3 C. D.
6.如图,在矩形 中, ,在 上取一点 ,连接 、 ,将 沿 翻折,使点 落在 处,线段 交 于点 ,将 沿 翻折,使点 的对应点 落在线段 上,若点 恰好为 的中点,则线段 的长为( )
A. B. C. D.
7.若一个四边形的两条对角线相等,我们则称这个四边形为对角线四边形.下列图形是对角线四边形的是( )
A.一般四边形 B.平行四边形 C.矩形 D.菱形
8.要判断一个四边形门框是否为矩形,在下面四个拟定方案中,正确的方案是( )
A.测量对角线是否互相平分且垂直 B.测量对角线是否相互平分
C.测量对角线是否互相平分且相等 D.测量对角线是否互相垂直
9.下列判定矩形中,错误的是( )
A.三个角是直角是四边形是矩形 B.一个角是直角的平行四边形是矩形
C.对角线相等的四边形是矩形 D.对角线平分且相等的四边形是矩形
10.矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是( )
A.2 B.4 C.2 D.4
二、填空题
11.如图,在菱形ABCD中,对角线AC与BD相交于点O,且,,于点E,则 .
12.如图,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO= 度.
13.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 .
14.如图,已知正方形的边长为4,M是对角线上的一个动点(不与B,D重合),连接,过M分别作的垂线段垂足分别为E,F,则的最小值是 .
三、解答题
15.如图,在四边形 中, 、 、 、 分别是 、 、 、 的中点,且 .
求证:四边形 是矩形.
16.已知:如图,矩形ABCD中,DE交BC于E,且DE=AD,AF⊥DE于F.
求证:AB=AF.
17.如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
求证:AE⊥BF.
18.如图,正方形ABCD中,点E、F分别在BC、CD上,且△AEF是等边三角形.
求证:CE=CF.
19.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)试说明∠BAE=∠DAF;
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形,并说明你的理由.
20.如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
21.如图,在平行四边形中,边的垂直平分线交于点E,交的延长线于点F,连接,.
(1)求证:;
(2)求证:四边形是菱形.
22.已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
23.问题提出
(1)如图①,在Rt△ABC中,∠A=90°,AB=3,AC=4,在BC上找一点D,使得AD将△ABC分成面积相等的两部分,作出线段AD,并求出AD的长度;
问题探究
(2)如图②,点A、B在直线a上,点M、N在直线b上,且a∥b,连接AN、BM交于点O,连接AM、BN,试判断△AOM与△BON的面积关系,并说明你的理由;
解决问题
(3)如图③,刘老伯有一个形状为筝形OACB的养鸡场,在平面直角坐标系中,O(0,0)、A(4,0)、B(0,4)、C(6,6),是否在边AC上存在一点P,使得过B、P两点修一道笔直的墙(墙的宽度不计),将这个养鸡场分成面积相等的两部分?若存在,请求出直线BP的表达式;若不存在,请说明理由.
答案解析部分
1.【答案】D
【解析】【解答】根据平行四边形和菱形的性质得到A、B、C均正确,而D不正确,因为对角线互相垂直的四边形也可能是梯形,故选D.
【分析】主要考查了平行四边形和特殊平行四边形的特性,并利用性质解题.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.菱形的特性是:四边相等,对角线互相垂直平分.
2.【答案】D
【解析】【解答】解:据“一组邻边相等的平行四边形是菱形”, A选项少平行故不符合题意;
据“对角线互相平分且垂直的四边形是菱形”, B选项少对角线垂直故不符合题意;
据“对角线互相垂直的平行四边形是菱形”, C选项少平行不符合题意;
据“四条边都相等的四边形是菱形”,D选项与菱形的判定定理相同故符合题意;
故答案为:D.
【分析】根据菱形的定义和判定定理进行分析即可。
3.【答案】C
【解析】【解答】解:由题意可得:
故答案为:C
【分析】根据菱形的面积公式即可求出答案。
4.【答案】B
【解析】【解答】解: 四边形 是平行四边形,
,故A正确,
四边形 是平行四边形, ,
不能推出四边形 是菱形,故 错误,
四边形 是平行四边形, ,
四边形 是矩形,故C正确,
四边形 是平行四边形, , ,
四边形 是正方形.故D正确.
故答案为:B.
【分析】(1)根据平行四边形的对角线互相平分可得OA=OC,OB=OD;
(2)根据菱形的判定“一组邻边相等的平行四边形是菱形”可知当AB=CD时,四边形ABCD是菱形错误;
(3)根据一个角是直角的平行四边形是矩形可知 当∠ABC=90°时,四边形 是矩形;
(4)根据对角线相等且互相垂直的平行四边形是正方形可知,当 且 时,四边形 是正方形.
5.【答案】C
【解析】【解答】解:过B点作BF⊥CD,与DC的延长线交于F点,
则有△BCF≌△BAE(ASA),
则BE=BF,S四边形ABCD=S正方形BEDF=8,
∴BE= .
故答案为:C.
【分析】过B点作BF⊥CD,与DC的延长线交于F点,根据全等三角形的判定方法很容易利用ASA判断出△BCF≌△BAE,根据全等三角形的性质得出BE=BF,S△BCF=S△BAE,四边形BEDF是正方形,最后根据S四边形ABCD=S正方形BEDF即可列出方程,求解即可.
6.【答案】D
【解析】【解答】解:设 F长为
∵ 沿 翻折,点 落在 处, 沿 翻折,使点 的对应点 落在线段 上
∴A =AB=CD= D,
由全等三角形判定定理AAS可得
∴ F= ,
∵点 为 的中点
∴
得
故答案为:D。
【分析】设 F长为 ,根据图形沿着某条边折叠所得的两个图形全等,即可推出全等三角形对应的边和角相等,利用得出的结论,再推出 ,F是AD的中点,已知AB=1,再根据边之间的长度关系列出等式,∴ ,得 , .
7.【答案】C
【解析】【解答】解:在一般四边形、平行四边形、矩形、菱形中,只有矩形的对角线相等.故选:C.
【分析】根据矩形的对角线相等,即可解答.
8.【答案】C
【解析】【解答】A、对角线互相平分得到该四边形是平行四边形,而对角线互相垂直的平行四边形是菱形,故A不符合题意;
B、对角线互相平分得到该四边形是平行四边形,故B不符合题意;
C、对角线互相平分得到该四边形是平行四边形,对角线相等的平行四边形是矩形,故C符合题意;
D、对角线是否互相垂直无法判定是何特殊四边形,故D不符合题意.
故答案为:C
【分析】根据平行四边形的判定与性质、矩形的判定、菱形的判定,分别对各个选项进行判断即可。
9.【答案】C
【解析】【解答】解:A:三个角是直角的四边形是矩形正确,不符合题意;
B: 一个角是直角的平行四边形是矩形正确,不符合题意;
C:对角线相等的平行四边形是矩形 ,这里是四边形,所以错误,符合题意;
D:对角线平分且相等的四边形是矩形正确,不符合题意。
故答案为:C。
【分析】分别根据矩形的判定,判断各选项能不能得出矩形的结论,选择错误的选项即可。
10.【答案】B
【解析】【解答】解:如图,
∵矩形ABCD,
∴OA=OB,AC=2OA,
∵∠AOB=60°,
∴△ABO是等边三角形,
∴AO=AB=2,
∴AC=2×2=4.
故答案为:B
【分析】利用矩形的性质可证得OA=OB,AC=2OA,利用有一个角是60°的等腰三角形是等边三角形,可证得△ABO是等边三角形,可求出OA的长,然后求出AC的长.
11.【答案】
【解析】【解答】解:∵ 四边形ABCD是菱形,AC=6,BD=8,
∴AC⊥BD,,,
在中,根据勾股定理得,,
∵S菱形ABCD =AC×BD=BC×AE,
即S菱形ABCD =×6×8=5×AE,
∴AE=.
故答案为:.
【分析】根据菱形的性质:对角线互相垂直平分,可求得OB,OC的值,再根据勾股定理求得菱形的边长,最后再根据菱形的面积获得等式,进而求出高AE的值.
12.【答案】25
【解析】【解答】解:∵四边形ABCD是菱形,
∴OD=OB,∠COD=90°,
∵DH⊥AB,
∴OH=BD=OB,
∴∠OHB=∠OBH,
又∵AB∥CD,
∴∠OBH=∠ODC,
在Rt△COD中,∠ODC+∠DCO=90°,
在Rt△DHB中,∠DHO+∠OHB=90°,
∴∠DHO=∠DCO==25°,
故答案为:25.
【分析】根据菱形的对角线互相平分可得OD=OB,再根据直角三角形斜边上的中线等于斜边的一半可得OH=OB,然后根据等边对等角求出∠OHB=∠OBH,根据两直线平行,内错角相等求出∠OBH=∠ODC,然后根据等角的余角相等解答即可.
13.【答案】
【解析】【解答】解:如图,连接AC、CF,
∵正方形ABCD和正方形CEFG中,BC=1,CE=3,
∴AC= ,CF=3 , ∠ACD=∠GCF=45°,
∴∠ACF=90°,
由勾股定理得,AF= ,
∵H是AF的中点,
∴CH= AF= ×2 = .
故答案为: .
【分析】连接AC、CF,根据正方形形状得出AC、CF,∠ACD=∠GCF=45°,再求出∠ACF=90°,在利用勾股定理列式求出AF,再根据直角三角形些边上的中线等于斜边的一半解答即可。
14.【答案】
【解析】【解答】解:如图:延长FM交CD于P,连结AC交BD于O,
∵四边形为正方形,
∴BD平分又,则
∵BD平分所以易证得:四边形AFPD为矩形,则FP=AD,故
则当时,MC有最小值:故 的最小值是
故答案为:.
【分析】本题主要考查正方形的性质、角平分线的性质、点到直线的距离最小值为垂线段,延长FM交CD于P,连结AC交BD于O,根据正方形及角平分线的性质可得:从而得到:再根据点到直线的距离最小值为垂线段即可求解.
15.【答案】证明:∵点E、F、G、H分别是边AB、BC、CD、DA的中点,
∴EF= AC,GH= AC,
∴EF=GH,同理EH=FG
∴四边形EFGH是平行四边形;
又∵对角线AC、BD互相垂直,
∴EF与FG垂直.
∴四边形EFGH是矩形.
【解析】【分析】根据题意易证得 四边形EFGH是平行四边形,对角线AC、BD互相垂直, 可判定出 四边形EFGH是矩形.
16.【答案】证明:∵AF⊥DE.
∴∠AFE=90°.
∵在矩形ABCD中,AD∥BC,∠C=90°.
∴∠ADF=∠DEC.
∴∠AFE=∠C=90°.
∵AD=DE.
∴△ADF≌△DEC.
∴AF=DC.
∵DC=AB.
∴AF=AB
【解析】【分析】根据已知及矩形的性质利用AAS判定△ADF≌△DEC,从而得到AF=DC,因为DC=AB,所以AF=AB.
17.【答案】证明:∵E,F分别是正方形ABCD边BC,CD的中点, ∴CF=BE, 在Rt△ABE和Rt△BCF中, ∵ , ∴Rt△ABE≌Rt△BCF(SAS), ∴∠BAE=∠CBF, 又∵∠BAE+∠BEA=90°, ∴∠CBF+∠BEA=90°, ∴∠BGE=90°, ∴AE⊥BF.
【解析】【分析】由E,F分别是正方形ABCD边BC,CD的中点知CF=BE,证Rt△ABE≌Rt△BCF得∠BAE=∠CBF,根据∠BAE+∠BEA=90°即可得∠CBF+∠BEA=90°,据此即可得证.
18.【答案】证明:∵四边形ABCD是正方形,
∴AD=AB,∠D=∠B=90°,
∵△AEF是等边三角形,
∴AF=AE,
在Rt△ADF和Rt△ABE中,
,
∴Rt△ADF≌Rt△ABE(HL),
∴DF=BE,
∴CE=CF.
【解析】【分析】利用正方形的性质可得到 AD=AB,∠D=∠B=90°;再利用等边三角形的性质可得到AF=AE;再利用HL证明Rt△ADF≌Rt△ABE,利用全等三角形的对应边相等,可推出DF=BE,由此可证得结论.
19.【答案】(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
在Rt△ABE和Rt△ADF中,
∵ ,
∴Rt△ADF≌Rt△ABE(HL)
∴∠BAE=∠DAF;
(2)解:四边形AEMF是菱形,理由为:
证明:∵四边形ABCD是正方形,
∴∠BCA=∠DCA=45°(正方形的对角线平分一组对角),
BC=DC(正方形四条边相等),
∵BE=DF(已证),
∴BC﹣BE=DC﹣DF(等式的性质),
即CE=CF,
在△COE和△COF中,
,
∴△COE≌△COF(SAS),
∴OE=OF,又OM=OA,
∴四边形AEMF是平行四边形(对角线互相平分的四边形是平行四边形),
∵AE=AF,
∴平行四边形AEMF是菱形.
【解析】【分析】(1)求简单的角相等,可证两角所在的三角形全等,即证△ABE≌△ADF;(2)由于四边形ABCD是正方形,易得∠ECO=∠FCO=45°,BC=CD;联立(1)的结论,可证得EC=CF,根据等腰三角形三线合一的性质可证得OC(即AM)垂直平分EF;已知OA=OM,则EF、AM互相平分,再根据一组邻边相等的平行四边形是菱形,即可判定四边形AEMF是菱形.
20.【答案】(1)证明:∵ 四边形ABCD是平行四边形,
∴ CF∥ED,
∴ ∠FCG=∠EDG,
∵ G是CD的中点,
∴ CG=DG,
在△FCG和△EDG中, ,
∴ △FCG ≌△EDG(ASA),
∴ FG=EG,∵ CG=DG,
∴ 四边形CEDF是平行四边形
(2)3.5;2
【解析】【解答】解:(2)①当AE=3.5时,平行四边形CEDF是矩形,
理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=3,
∴BM=1.5,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5,
∵AE=3.5,
∴DE=1.5=BM,
在△MBA和△EDC中,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
故答案为:3.5;
②当AE=2时,四边形CEDF是菱形,
理由是:∵AD=5,AE=2
,
∴DE=3,
∵CD=3,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
∵四边形CEDF是平行四边形,
∴四边形CEDF是菱形,
故答案为:2
① 当AE=3.5cm时,四边形CEDF是矩形.
② 当AE=2cm时,四边形CEDF是菱形.
【分析】(1)根据“ASA”可证△FCG ≌△EDG,可得FG=EG,根据平行四边形的判定方法即可推出;
(2)①过A作AM⊥BC于M,根据“SAS”可证△MBA≌△EDC,可得∠CED=∠AMB=90°,根据矩形的判定推出即可;
②先求出△CDE是等边三角形,可得CE=DE,利用一组邻边相等的平行四边形是菱形即证.
21.【答案】(1)证明:四边形是平行四边形,
,
,
垂直平分,
,
在和中,
,
;
(2)证明:,
,
,
四边形是平行四边形,
又,
平行四边形是菱形.
【解析】【分析】(1)由平行四边形的小组可得AD∥BC,由平行线的性质可得∠AEG=∠BFG,由线段垂直平分线的性质可得AG=BG,用角角边可证;
(2)由(1)中的全等三角形的性质可得AE=BF,根据一组对边平行且相等的四边形是平行四边形可得四边形AFBE是平行四边形,结合已知根据对角线互相垂直的平行四边形是菱形可得平行四边形AFBE是菱形.
22.【答案】(1)证明:∵四边形ABCD是矩形,∴∠A=∠D=90°,AB=DC,∵M是AD的中点,
∴AM=DM,
在△ABM和△DCM中, ,
∴△ABM≌△DCM(SAS);
(2)解:四边形MENF是菱形;理由如下:由(1)得:△ABM≌△DCM,
∴BM=CM,
∵E、F分别是线段BM、CM的中点,
∴ME=BE= BM,MF=CF= CM,
∴ME=MF,
又∵N是BC的中点,∴EN、FN是△BCM的中位线,∴EN= CM,FN= BM,
∴EN=FN=ME=MF,
∴四边形MENF是菱形.
【解析】【分析】(1)M是边AD的中点,得到AM=DM,根据矩形的性质,得到∠A=∠D,AB=DC,由SAS得到△ABM≌△DCM;(2)由(1)知△ABM≌△DCM,得到对应边BM=CM,由E、F分别是线段BM、CM的中点,得到ME=MF,再根据三角形中位线定理,得到EN=FN=ME=MF,得到四边形MENF是菱形.
23.【答案】(1)解:如图①,取BC边的中点D,连接AD,则线段AD即为所求.
在Rt△ABC中,∠BAC=90°,AB=3,AC=4,
∴BC=,
∵点D为BC的中点,
∴AD=BC=.
(2)解:S△AOM=S△BON,理由如下:
由图可知,S△AOM=S△ABM﹣S△AOB,S△BON=S△ABN﹣S△AOB,
如图②,过点M作MD⊥AB于点D,过点N作NE⊥AB于点E,
∴MD∥NE,∠MDE=90°,
又∵MN∥DE,
∴四边形MDEN是矩形,
∴MD=NE,
∵S△ABM=,S△ABN=,
∴S△ABM=S△ABN,
∴S△AOM=S△BON.
(3)解:存在,直线BP的表达式为:y=x+4.
如图③,连接AB,过点O作OF∥AB,交CA的延长线于点F,连接BF,交OA于点G,
由(2)的结论可知,S△OBG=S△AFG,
∴S四边形OACB=S△BCF,
取CF的中点P,作直线BP,直线BP即为所求.
∵A(4,0),B(0,4),C(6,6),
∴线段AB所在直线表达式为:y=﹣x+4,
线段AC所在直线的表达式为:y=3x﹣12,
∵OF∥AB,且直线OF过原点,
∴直线OF的表达式为:y=﹣x,
联立,解得,
∴F(3,﹣3),
∵点P是CF的中点,
∴P,
∴直线BP的表达式为:y=x+4.
【解析】【分析】(1)利用三角形的中线分得的两个三角形的面积相等,可知取BC边的中点D,连接AD即可;利用勾股定理求出BC的长,再利用直角三角形斜边上的中线等于斜边的一半可得AD的长;
(2)观察图形可知S△AOM=S△ABM﹣S△AOB,S△BON=S△ABN﹣S△AOB,利用利用平行线间的距离处处相等及同底等高的两个三角形的面积相等,可证得△ABM的面积=△ABN的面积,由此可证得结论;
(3)连接AB,过点O作OF∥AB,交CA的延长线于点F,连接BF,交OA于点G,由(2)的结论可证得 S四边形OACB=S△BCF,取CF的中点P,作直线BP,直线BP即为所求;利用待定系数法求出直线AB,AC的函数解析式,利用OF∥AB,可得到直线OF的函数解析式,将直线OF和直线AC联立方程组,解方程组,可得到点F的坐标,利用线段中点坐标可求出点P的坐标,然后利用待定系数法求出直线BP的函数解析式.
1 / 1
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
