初中数学浙教版九年级上册3.3垂径定理第一课时(17张ppt)
文档属性
| 名称 | 初中数学浙教版九年级上册3.3垂径定理第一课时(17张ppt) | 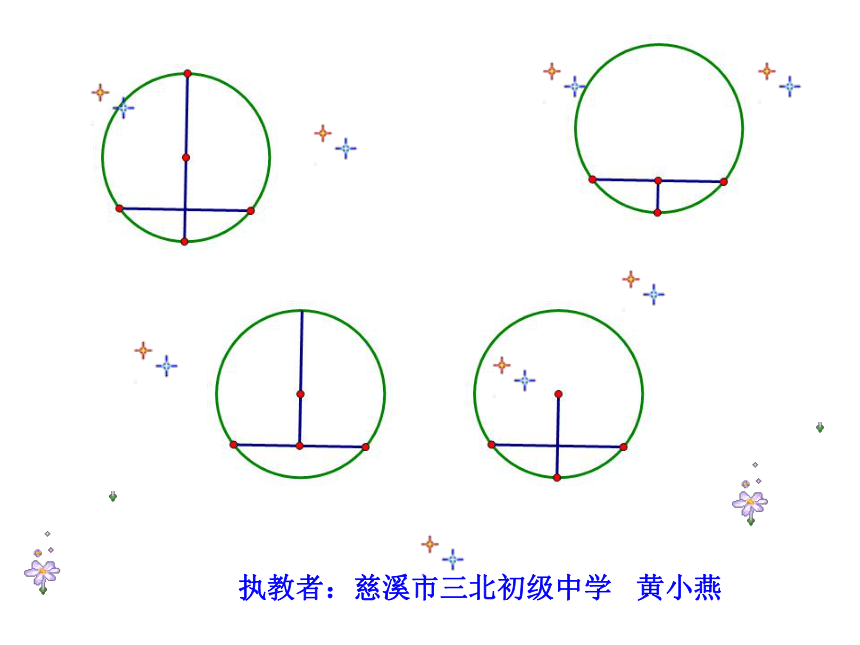 | |
| 格式 | zip | ||
| 文件大小 | 591.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-20 11:31:49 | ||
图片预览



文档简介
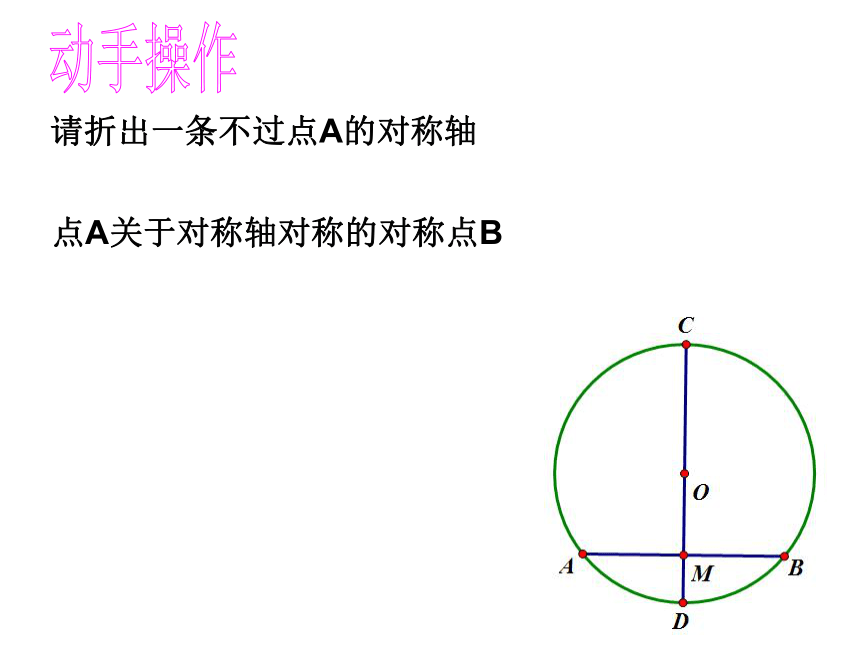
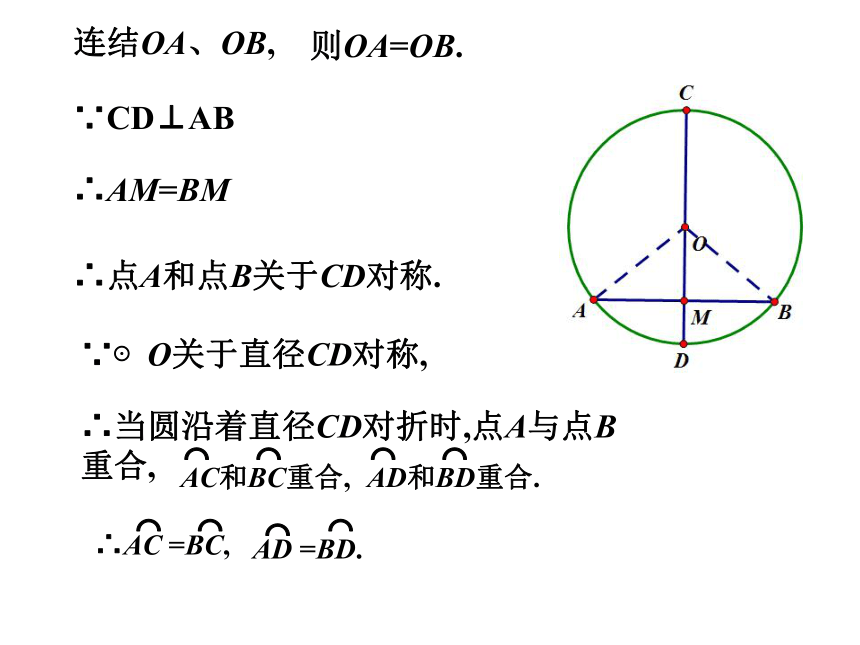
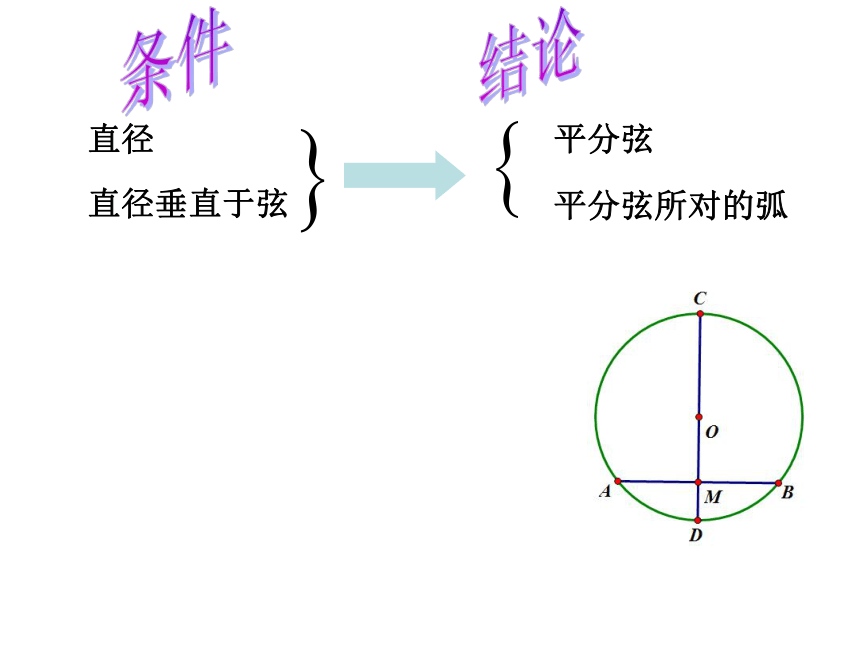
课件17张PPT。执教者:慈溪市三北初级中学 黄小燕请折出一条不过点A的对称轴动手操作点A关于对称轴对称的对称点B 连结OA、OB,则OA=OB.∵CD⊥AB∴AM=BM∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,条件结论直径直径垂直于弦平分弦平分弦所对的弧3.3 垂径定理
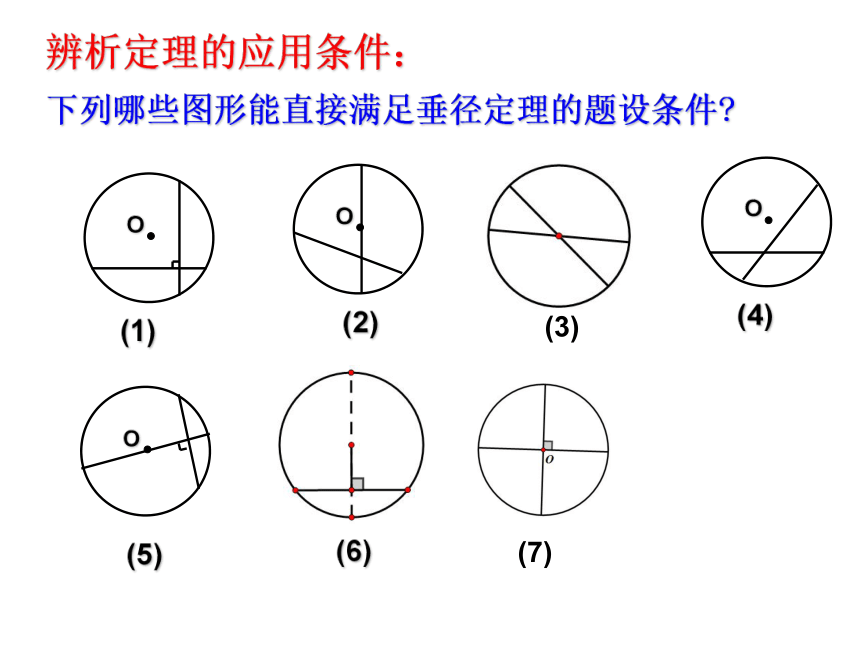
(第1课时)浙教版九年级(上册)垂径定理辨析定理的应用条件:下列哪些图形能直接满足垂径定理的题设条件?(6)(7)(3)辨一辨 如图,AB是⊙0的直径,CD为弦,CD⊥AB于E,则下列结论中不一定成立的是( )
A.∠COE=∠DOE B.CE=DE
C.OE=BE D.BD=BCC 分一条弧成相等的两条弧的点叫做这条弧的中点AB变式一: 求弧AB的四等分点.例2:如图,一条排水管的截面.已知排水管的半径OB=10,水面宽AB=16.求截面圆心到水面的距离OC. 弦心距:圆心到一条弦的距离1、已知⊙O的半径为13cm,圆心O到弦AB的弦心距为5cm,
求弦AB的长。2、 ⊙O的弦长AB的长为8cm,弦AB的弦心距为3cm,
则⊙O的半径为 。小结:半径(r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:基本图形如图CD是⊙O的直径, 弦AB⊥CD,垂足为M,
2、若AB=16,CM=4,求OM的长.1、若CD=10,弦AB=8,则DM的长为______.1.本节课主要内容:垂径定理.2.垂径定理的应用:(1)作图;(2)计算和证明.3.解题的主要方法:总结回顾 1、如图,C为⊙O内的一点,你能画过点C最长的弦吗?你能画过点C最短的弦吗?M是弦AB上的动点,则OM的长的取值范围是 .过点C且长为整数值的弦有几条?若半径是5cm,OC=3cm,如图,已知圆的半径为13 cm,两弦AB∥CD,AB=24 cm,CD=10 cm,则两弦AB,CD的距离是 ( )
A.7 cm B.17 cm
C.12 cm D.7 cm或17 cm过点O作OE⊥AB,延长OE交CD于点F∵AB//CD
∴OF⊥CD已知圆的半径为13 cm,两弦AB∥CD,AB=24 cm,CD=10 cm,则两弦AB,CD的距离是 ( )
A.7 cm B.17 cm
C.12 cm D.7 cm或17 cm再见!
(第1课时)浙教版九年级(上册)垂径定理辨析定理的应用条件:下列哪些图形能直接满足垂径定理的题设条件?(6)(7)(3)辨一辨 如图,AB是⊙0的直径,CD为弦,CD⊥AB于E,则下列结论中不一定成立的是( )
A.∠COE=∠DOE B.CE=DE
C.OE=BE D.BD=BCC 分一条弧成相等的两条弧的点叫做这条弧的中点AB变式一: 求弧AB的四等分点.例2:如图,一条排水管的截面.已知排水管的半径OB=10,水面宽AB=16.求截面圆心到水面的距离OC. 弦心距:圆心到一条弦的距离1、已知⊙O的半径为13cm,圆心O到弦AB的弦心距为5cm,
求弦AB的长。2、 ⊙O的弦长AB的长为8cm,弦AB的弦心距为3cm,
则⊙O的半径为 。小结:半径(r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:基本图形如图CD是⊙O的直径, 弦AB⊥CD,垂足为M,
2、若AB=16,CM=4,求OM的长.1、若CD=10,弦AB=8,则DM的长为______.1.本节课主要内容:垂径定理.2.垂径定理的应用:(1)作图;(2)计算和证明.3.解题的主要方法:总结回顾 1、如图,C为⊙O内的一点,你能画过点C最长的弦吗?你能画过点C最短的弦吗?M是弦AB上的动点,则OM的长的取值范围是 .过点C且长为整数值的弦有几条?若半径是5cm,OC=3cm,如图,已知圆的半径为13 cm,两弦AB∥CD,AB=24 cm,CD=10 cm,则两弦AB,CD的距离是 ( )
A.7 cm B.17 cm
C.12 cm D.7 cm或17 cm过点O作OE⊥AB,延长OE交CD于点F∵AB//CD
∴OF⊥CD已知圆的半径为13 cm,两弦AB∥CD,AB=24 cm,CD=10 cm,则两弦AB,CD的距离是 ( )
A.7 cm B.17 cm
C.12 cm D.7 cm或17 cm再见!
同课章节目录
