初中数学浙教版八年级上册2.6 直角三角形第一课时课件(17张ppt)
文档属性
| 名称 | 初中数学浙教版八年级上册2.6 直角三角形第一课时课件(17张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 629.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-20 11:45:52 | ||
图片预览


文档简介
课件17张PPT。2.6直角三角形(1)浙教版数学 八年级(上)第二章 特殊三角形直角三角形的定义: 有一个角是直角的三角形
叫直角三角形.日常生活中常见的
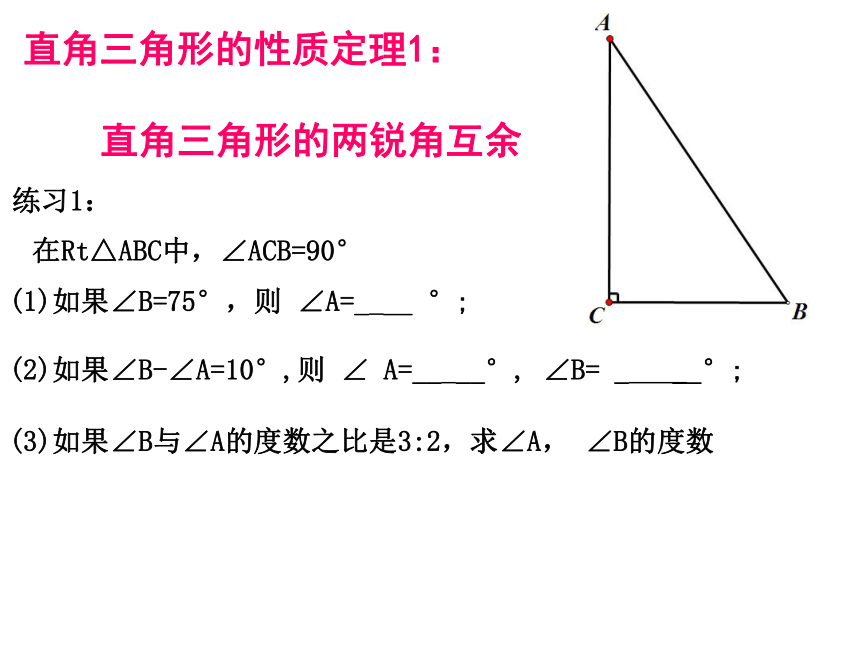
直角三角形有哪些?∠ACB是一个直角,记为Rt∠ACB△ABC是直角三角形,记为Rt△ABC直角三角形的两个锐角之间有什么关系?直角三角形的性质定理1:
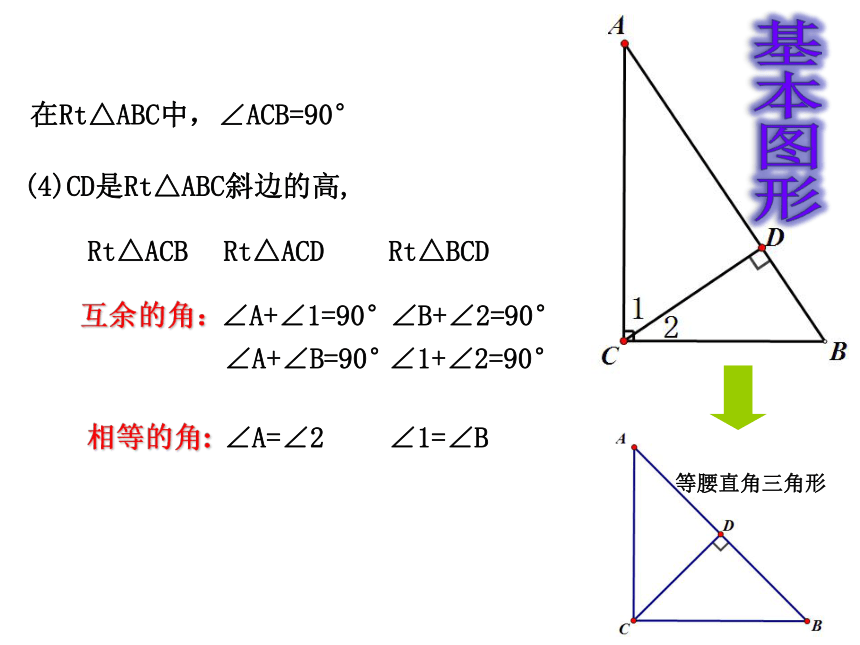
直角三角形的两锐角互余在Rt△ABC中,∠ACB=90°(1)如果∠B=75°,则 ∠A=_ __ °;练习1:(2)如果∠B-∠A=10°,则 ∠ A=__ __°, ∠B= _ __°;(3)如果∠B与∠A的度数之比是3:2,求∠A, ∠B的度数在Rt△ABC中,∠ACB=90°(4)CD是Rt△ABC斜边的高,∠A+∠1=90°Rt△ACDRt△BCD∠A+∠B=90°∠1+∠2=90°∠B+∠2=90°∠A=∠2∠1=∠B互余的角:相等的角:Rt△ACB基本图形等腰直角三角形合作学习如图,在△ABC中,∠ACB=90°,将△ABC
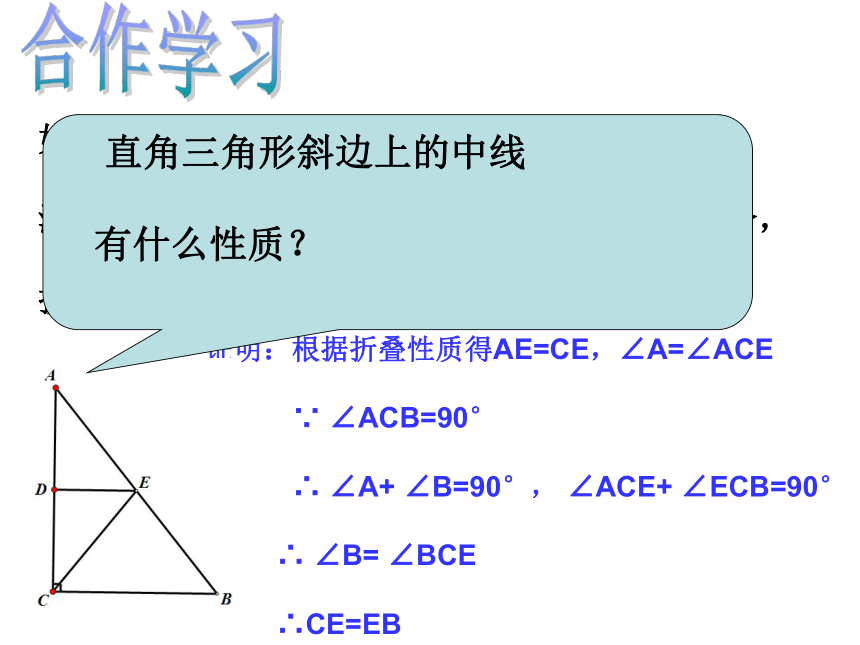
沿某条直线折叠,使直角边的两个端点A与C重合,
折痕为DE.试证明CE=EB.证明:根据折叠性质得AE=CE,∠A=∠ACE
∵ ∠ACB=90°
∴ ∠A+ ∠B=90°, ∠ACE+ ∠ECB=90°
∴ ∠B= ∠BCE
∴CE=EB 直角三角形斜边上的中线
有什么性质?性质定理2:
直角三角形斜边上的中线等于斜边的一半几何语言:∵ ∠ACB=90°,∴CE是AB边上的中线AE=BE直角三角形斜边上的中线等于斜边的一半性质定理2练习2:1、判断下列命题是真命题还是假命题:(1)在△ACB中,CD是AB边上的中线,则 .( )(2)在Rt△ACB中,∠ACB=90°,D是AB边上的一点,
则 .( )(3)在Rt△ACB中,∠ACB=90°,AD是BC上的中线,
则 .( )D假命题假命题假命题直角斜边中线性质定理2练习2:(1)若AB=10,则AE= , CE= ;(2)若CE=4,则AB= ;∠A+∠2=90°等腰△ACE等腰△BCE∠A+∠B=90°∠1+∠2=90°∠B+∠1=90°∠A=∠1∠B=∠2互余的角:相等的角:相等的线段:基本图形直角三角形斜边上的中线等于斜边的一半2、在RT△ACB中, ∠ACB=90°,点E是AB边上的中点(3)若∠A=30°,有哪些相等的线段?练习2:2、在RT△ACB中, ∠ACB=90°,点E是AB边上的中点△ACE是等腰三角形,△CEB是等边三角形例1 如图,一名滑雪运动员沿倾斜角为30°的斜坡,从A滑行至B。已知AB=200m,问这名滑雪运动员的高度下降了多少m? 将这个性质归纳概括成结论: 在直角三角形中,
30°角所对的直角边等于斜边的一半。
∵∠ACB=90° ,∠A=30°
∴几何语言:1.直角三角形的两个锐角互余.
2.直角三角形斜边上的中线等于斜边的一半
在直角三角形中, 30°角所对的直角边等于斜边的一半。
小 结基本图形在Rt△ABC与Rt△ACE中,∠ABC=∠AEC=90 °,点M是AC边上的中点,连结BM、EM、 求证:(1)BM=EM(已知)∵ ∠ ABC= ∠ AEC=90° M是AC边上的中点(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)∴ BM= EM又∵ P是BE边上的中点∴ MP ⊥ BE (等腰三角形三线合一)(2)MP⊥BE .BE,点P是BE的中点.证明:自我挑战☆★☆★☆★☆★证明:∵ ∠ ABC= ∠ AEC=90 ° M是AC边上的中点∴ BM= EM又∵ P是BE边上的中点∴ MP ⊥BE (已知)(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)(等腰三角形三线合一)在Rt△ABC与Rt△ACE中,∠ABC=∠AEC=90°,点M是AC边上的中点,连结BM、EM、BE,点P是BE的中点. 求证:MP⊥BE .变在△ACD中,AE、CB分别是边CD、AD边上的高,M、P分别是AC、BE的中点.
求证:MP⊥BE .证明:∵ ∠AEC= ∠ABC=90 ° M是AC边上的中点∴ ME= MB又∵ P是BE边上的中点∴ MP ⊥ BE (已知)(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)(等腰三角形三线合一)连结ME、MB再变
叫直角三角形.日常生活中常见的
直角三角形有哪些?∠ACB是一个直角,记为Rt∠ACB△ABC是直角三角形,记为Rt△ABC直角三角形的两个锐角之间有什么关系?直角三角形的性质定理1:
直角三角形的两锐角互余在Rt△ABC中,∠ACB=90°(1)如果∠B=75°,则 ∠A=_ __ °;练习1:(2)如果∠B-∠A=10°,则 ∠ A=__ __°, ∠B= _ __°;(3)如果∠B与∠A的度数之比是3:2,求∠A, ∠B的度数在Rt△ABC中,∠ACB=90°(4)CD是Rt△ABC斜边的高,∠A+∠1=90°Rt△ACDRt△BCD∠A+∠B=90°∠1+∠2=90°∠B+∠2=90°∠A=∠2∠1=∠B互余的角:相等的角:Rt△ACB基本图形等腰直角三角形合作学习如图,在△ABC中,∠ACB=90°,将△ABC
沿某条直线折叠,使直角边的两个端点A与C重合,
折痕为DE.试证明CE=EB.证明:根据折叠性质得AE=CE,∠A=∠ACE
∵ ∠ACB=90°
∴ ∠A+ ∠B=90°, ∠ACE+ ∠ECB=90°
∴ ∠B= ∠BCE
∴CE=EB 直角三角形斜边上的中线
有什么性质?性质定理2:
直角三角形斜边上的中线等于斜边的一半几何语言:∵ ∠ACB=90°,∴CE是AB边上的中线AE=BE直角三角形斜边上的中线等于斜边的一半性质定理2练习2:1、判断下列命题是真命题还是假命题:(1)在△ACB中,CD是AB边上的中线,则 .( )(2)在Rt△ACB中,∠ACB=90°,D是AB边上的一点,
则 .( )(3)在Rt△ACB中,∠ACB=90°,AD是BC上的中线,
则 .( )D假命题假命题假命题直角斜边中线性质定理2练习2:(1)若AB=10,则AE= , CE= ;(2)若CE=4,则AB= ;∠A+∠2=90°等腰△ACE等腰△BCE∠A+∠B=90°∠1+∠2=90°∠B+∠1=90°∠A=∠1∠B=∠2互余的角:相等的角:相等的线段:基本图形直角三角形斜边上的中线等于斜边的一半2、在RT△ACB中, ∠ACB=90°,点E是AB边上的中点(3)若∠A=30°,有哪些相等的线段?练习2:2、在RT△ACB中, ∠ACB=90°,点E是AB边上的中点△ACE是等腰三角形,△CEB是等边三角形例1 如图,一名滑雪运动员沿倾斜角为30°的斜坡,从A滑行至B。已知AB=200m,问这名滑雪运动员的高度下降了多少m? 将这个性质归纳概括成结论: 在直角三角形中,
30°角所对的直角边等于斜边的一半。
∵∠ACB=90° ,∠A=30°
∴几何语言:1.直角三角形的两个锐角互余.
2.直角三角形斜边上的中线等于斜边的一半
在直角三角形中, 30°角所对的直角边等于斜边的一半。
小 结基本图形在Rt△ABC与Rt△ACE中,∠ABC=∠AEC=90 °,点M是AC边上的中点,连结BM、EM、 求证:(1)BM=EM(已知)∵ ∠ ABC= ∠ AEC=90° M是AC边上的中点(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)∴ BM= EM又∵ P是BE边上的中点∴ MP ⊥ BE (等腰三角形三线合一)(2)MP⊥BE .BE,点P是BE的中点.证明:自我挑战☆★☆★☆★☆★证明:∵ ∠ ABC= ∠ AEC=90 ° M是AC边上的中点∴ BM= EM又∵ P是BE边上的中点∴ MP ⊥BE (已知)(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)(等腰三角形三线合一)在Rt△ABC与Rt△ACE中,∠ABC=∠AEC=90°,点M是AC边上的中点,连结BM、EM、BE,点P是BE的中点. 求证:MP⊥BE .变在△ACD中,AE、CB分别是边CD、AD边上的高,M、P分别是AC、BE的中点.
求证:MP⊥BE .证明:∵ ∠AEC= ∠ABC=90 ° M是AC边上的中点∴ ME= MB又∵ P是BE边上的中点∴ MP ⊥ BE (已知)(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)(等腰三角形三线合一)连结ME、MB再变
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
