九年级数学浙教版上册 第1章二次函数单元复习(共29张PPT)
文档属性
| 名称 | 九年级数学浙教版上册 第1章二次函数单元复习(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 554.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-21 14:12:57 | ||
图片预览






文档简介
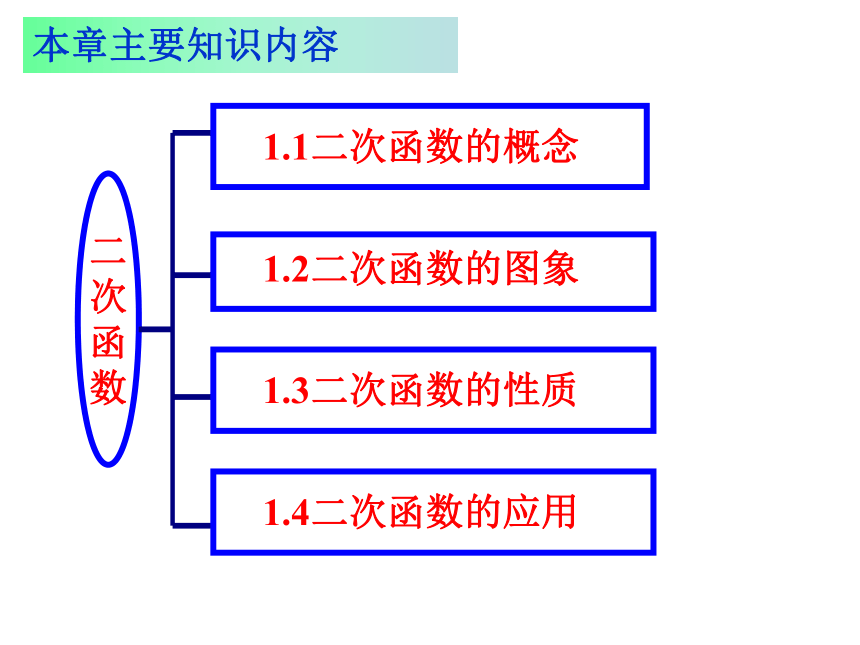
课件29张PPT。第1章 二次函数 复习本章主要知识内容二
次
函
数1.1 二次函数1.概念:形如y=ax2+bx+c(a、b、c为常数,且a≠0)的函数
叫做二次函数,其中a称二次项系数,b称一次项系数,
c称常数项.特别注意:二次项系数a不能为0.2.二次函数的表达式和自变量的取值范围(2)根据实际问题列出二次函数的关系式,但要注意考
虑自变量的取值范围,自变量的取值范围应使实际问
题有意义.(1)会由x、y的3组对应值求出二次函数的表达式.练习1.下列函数表达式中,一定为二次函数的是( ) C2.已知函数y=(m2+m)x2+mx+4为二次函数,则m的取值
范围是( ) A.m≠0 B.m≠-1 C.m≠0,且m≠-1 D.m=-1C3.矩形的周长为24cm,其中一边为xcm(其中x>0),
面积为ycm2,则这样的矩形中y与x的关系可以写成
( ) A.y=x2 B.y=(12-x)x
C. y=12-x2 D.y=2(12-x)B1.2二次函数的图象1.画二次函数图象的一般步骤:①列表:列出自变量与函数的对应值;②描点:建立适当的直角坐标系,并以表中各组对应
值作为点的坐标,在直角坐标系中描出相应的点;③连线:用平滑曲线顺次连结各点.2.二次函数的图象(1)二次函数y=ax2+bx+c(a≠0)的图象是一条关于
直线 对称的抛物线,抛物线与对称轴的交点
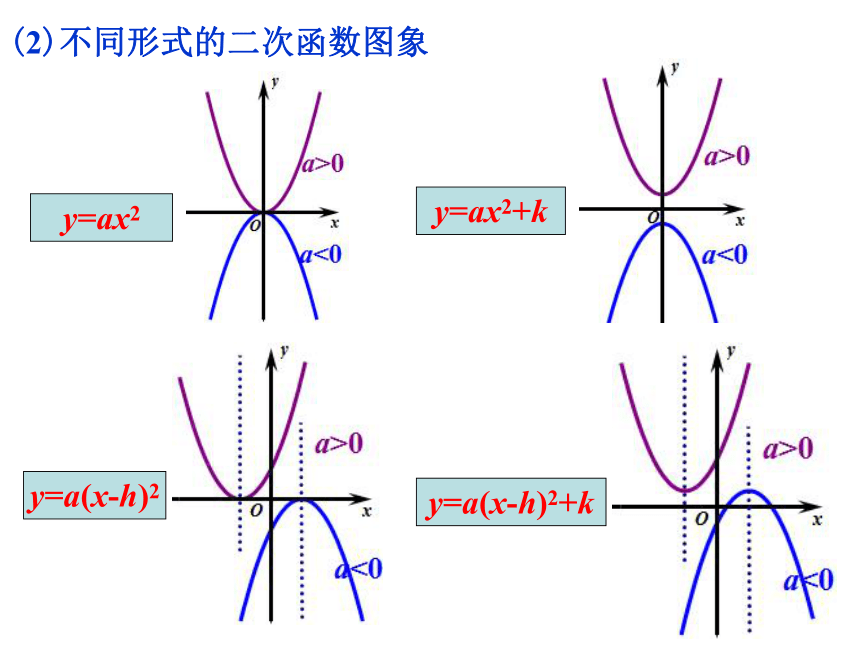
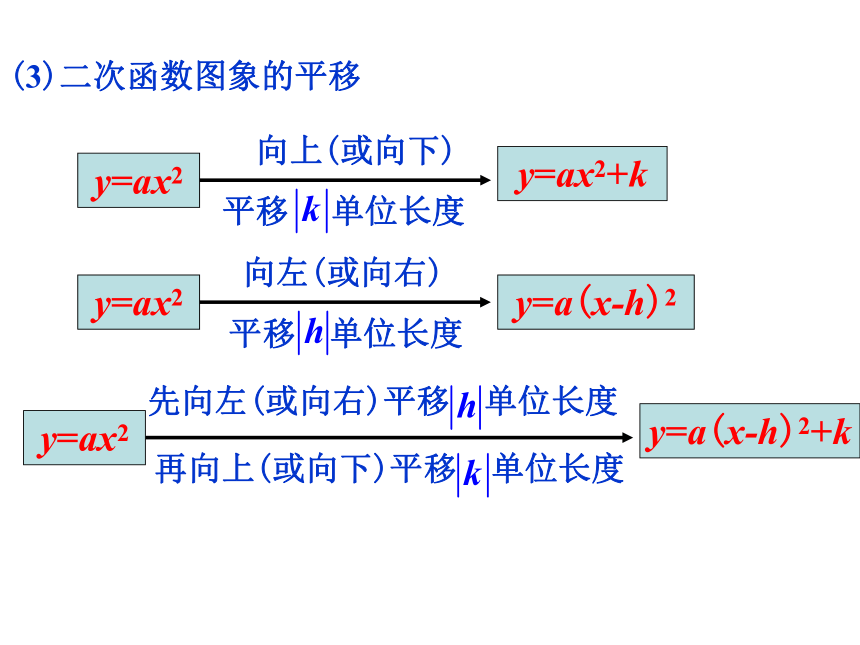
是抛物线的顶点.(2)不同形式的二次函数图象y=ax2y=ax2+ky=a(x-h)2y=a(x-h)2+k(3)二次函数图象的平移y=ax2向上(或向下)平移 单位长度y=ax2+ky=ax2向左(或向右)y=a(x-h)2平移 单位长度y=ax2再向上(或向下)平移 单位长度y=a(x-h)2+k先向左(或向右)平移 单位长度练习1.将抛物线y=-x2向上平移2个单位后,得到的
函数表达式是( ) A.y=-x2+2 B.y=-(x+2)2
C.y=-(x-1)2 D.y=-x2-2A2.将二次函数y=-2x2的图象平移后,可得到二次函
数y=-2(x+3)2的图象,平移的方法是( ) A.向上平移3个单位 B.向下平移3个单位
C.向左平移3个单位 D.向右平移3个单位C3.将抛物线y=(x-1)2+2向上平移2个单位长度,再向右
平移3个单位长度后,得到的抛物线的解析式为( ) A.y=(x-1)2+4 B. y=(x-4)2+4
C.y=(x+2)2+6 D.y=(x-4)2+6B(5)抛物线y=ax2+bx+c(a≠0)的对称轴、顶点坐标①通过配方法将y=ax2+bx+c化成顶点式y=a(x-h)2+k;对称轴为直线x=h,顶点坐标为(h,k).②直接用公式法:对称轴为直线顶点坐标为(4)抛物线y=ax2+bx+c(a≠0)的开口方向当a>0时,抛物线开口向上,顶点是抛物线的最低点;当a<0时,抛物线开口向下,顶点是抛物线的最高点.练习1.已知二次函数y=a(x-1)2-c的图象如图所示,
则一次函数y=ax+c的大致图象可能是( )A2.把二次函数y=-2x2-4x+10,化成y=a(x-h)2+k的形式
是_______________________. y=-2(x+1)2+123.抛物线y=-x2+4x-3 的对称轴是直线__________,
顶点坐标为__________.(2,1)x=2(6)二次函数y=ax2+bx+c的系数a、b、c与图象的关系①a的符号决定抛物线的开口方向:当a>0时,抛物
线开口向上;当a<0时,抛物线开口向下,a的绝对
值决定着抛物线的形状、大小,当a的绝对值相等时,
抛物线的形状、大小相同;当a的绝对值越大时,抛
物线的开口越小.②a、b符号决定着抛物线的对称轴位置a、b同号对称轴在y轴左侧a、b异号对称轴在y轴右侧b=0对称轴是y轴③c的符号决定着抛物线与y轴的交点位置c>0与y轴交点在x轴的上方c<0c>0与y轴交点在x轴的下方抛物线必经过坐标原点已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,
对称轴是直线x=-1,下列结论: ①abc<0;②2a+b=0;
③a-b+c>0;④b2-4ac>0.其中正确的是( )A.①② B.只有①
C.③④ D.①④D练习1.3二次函数的性质1.二次函数y=ax2+bx+c(a≠0)的增减性(1)在a>0,抛物线开口向上的情况x随x的增大而增大x随x的增大而减小(2)在a<0,抛物线开口向下的情况x随x的增大而减小x随x的增大而增大说明:二次函数的增减性可结合二次函数的大致图象进行分析.1.下列函数:①y=-3x2;②y=2x2-1;③y=(x-2)2;
④y=-x2+2x+3.当x<0时,其中y随x的增大而增大的
函数有( ) 练习A.4个 B.3个 C.2个 D.1个 C3.已知二次函数y=x2+(m-1)x+1,当x>1时,y随x的
增大而增大,则m的取值范围是( )A.m=-1 B.m=3 C.m≤-1 D.m≥-12.在二次函数y=- (x-2)2+3的图象上有两点(-1,y1),
(1,y2),则y1与y2的大小关系是( )A. y1<y2 B. y1=y2 C. y1>y2 D.不能确定AD①通过配方法将y=ax2+bx+c化成顶点式y=a(x-h)2+k;若a>0,则函数y有最小值,当x=h时,y最小值=k; 若a<0,则函数y有最大值,当x=h时,y最大值=k . ②直接用公式法:2.二次函数的最大(小)值3.二次函数与一元二次方程的关系②b2-4ac的符号决定着抛物线与x轴的交点情况b2-4ac>0与x轴有两个交点b2-4ac=0与x轴有一个交点b2-4ac<0与x轴没有交点①对于二次函数y=ax2+bx+c(a≠0),如果令y=0,则ax2+bx+c=0抛物线y=ax2+bx+c与x轴的交点的横坐标即为一元二次方
程ax2+bx+c=0的两个根;一元二次方程ax2+bx+c=0的
根即为抛物线y=ax2+bx+c与x轴交点的横坐标,练习1.已知二次函数y=ax2+bx+c(a≠0)的图象如
图所示,下列说法错误的是( ) A.图象关于直线x=1对称
B.函数y=ax2+bx+c(a≠0)的
最小值是-4
C.抛物线y=ax2+bx+c(a≠0)与x轴
的两个交点的横坐标分别是-1,3
D.当x<1时,y随x的增大而增大D3.已知抛物线y=x2-(k-1)x-3k-2与x轴交于A(a,0),
B(b,0)两点,且a2+b2=17,则k的值为_______.-6或22.已知函数y=(k-3)x2+2x+1的图象与x轴有交点,则k的
取值范围是( )A.k<4 B.k≤4 C.k<4且k≠3 D.k≤4且k≠3B4.二次函数表达式的求法1.已知二次函数的图象经过点(-1,5),(0,-4)
和(1,1),则这个二次函数的表达式( )练习A.y=-6x2+3x+4 B.y=-2x2+3x-4
C.y=x2+2x-4 D.y=2x2+3x-4D3.若二次函数的图象的顶点坐标为(2,-1),抛物线
过点(0,3),则二次函数的解析式是( )4.已知二次函数的图象与x轴的两个交点A、B关于直线
x=-1对称,且AB=6,顶点在函数y=2x的图象上,
则这个二次函数的表达式为__________________. C2.顶点为(6,0),开口向下,开口的大小与函数y= x2
的图象相同的抛物线所对应的函数表达式是( ) D1.将进货单价为70元的某种商品按零售价100元/个售出
时每天能卖出20个,若这种商品的零售价在一定范围
内每降价1元,其日销售量就增加1个,为了获得最大
利润,则应降价( )1.4二次函数的应用二次函数在实际问题中的应用A.5元 B.10元 C.15元 D.20元2.某公司在甲、乙两地同时销售某种品牌的汽车.已知在
甲、乙两地的销售利润y(万元)与销售量x(辆)之间分别
满足:y1=-x2+10x,y2=2x,若该公司在甲、乙两地共
销售15辆该品牌的汽车,则能获得的最大利润是( ) A.30万元 B.40万元 C.45万元 D.46万元AD3.某商场试销一种成本为每件60元的服装,规定试销期
间销售单价不低于成本单价,且获利不得高于45%,经
试销发现,销售量y(件)与销售单价x(元)符合一次
函数y=kx+b,且x=65时,y=55;x=75时,y=45;(3)若该商场所获得利润不低于500元,试确定销售单
价x的范围.(2)若该商场获得利润为W元,试写出利润W与销售单
价x之间的关系;销售单价定为多少时,商场可获得最
大利润,最大利润是多少元?(1)求一次函数的解析式;解:(1)∵把x=65,y=55;x=75,y=45解得:∴所求一次函数的解析式为y=-x+120,(2)W=(x-60)(-x+120)
=-x2+180x-7200
=-(x-90)2+900,代入y=kx+b得:由图象可知,要使该商场获得利润不低于500元,销售
单价应在70元到110元之间,而60≤x≤87,∴当销售单价定为87元时,商场可获得最大利润,
最大利润是891元;∵抛物线的开口向下,∴当x<90时,W随x的增大而增大,又∵60≤x≤87,∴当x=87时,W=-(87-90)2+900=891,(3)由W=500,得500=-x2+180x-7200,整理得:x2-180x+7700=0,解得:x1=70,x2=110,所以,销售单价x的范围是70≤x≤87.二次函数在几何问题中的应用1.为了节省材料,某水产养殖户利用水库的岸堤(岸堤
足够长)为一边,用总长为80m的围网在水库中围成了
如图所示的①②③三块矩形区域,而且这三块矩形区
域的面积相等.设BC的长度为xm,矩形区域ABCD的
面积为ym2.(2)x为何值时,y有最大值?最大值是多少?(1)求y与x之间的函数关系式,并注明自变量x的取值范围;(1)∵三块矩形区域的面积相等, 解:∴矩形AEFD面积是矩形BCFE面积的2倍,∴AE=2BE,设BE=a,则AE=2a,∴8a+2x=80,∴a=﹣ x+10,2a=﹣ x+20,∴y=(﹣ x+20)x+(- x+10)x=﹣ x2+30x,∴x<40,则y=﹣ x2+30x(0<x<40);∵a=﹣ x+10>0,(2)∵y=﹣ x2+30x=﹣ (x﹣20)2+300(0<x<40),且二次项系数为﹣ <0,∴当x=20时,y有最大值,最大值为300平方米.3.如图,在平面直角坐标系xOy中,直线y=x-1与抛物线
C1:y=x2-2x-1相交于A、C两点,过点A作AB∥x轴
交抛物线于点B.(3)若抛物线C2:y=ax(a≠0)与线段AB恰有一个
公共点,结合函数图象,求a的取值范围.(2)求△ABC的面积;(1)求点A、C的坐标;∴S△ABC= AB×CD= ×4×3=6;(1)由解:得,∴点A、C的坐标分别为(3,2),(0,-1);(2)由题意知:点A与B关于抛物线C1的对称轴对称,∵抛物线C1的对称轴为x=1,且A(3,2),∴B(-1,2),∴AB=4,设直线AB与y轴交于点D,则CD=1+2=3,(3)如图,∴a的取值范围为 ≤a<2.把B(-1,2)代入y=ax2得:a=2,把A(3,2)代入y=ax2得:a= ,当C2过点A点,B点临界点时,再见!
次
函
数1.1 二次函数1.概念:形如y=ax2+bx+c(a、b、c为常数,且a≠0)的函数
叫做二次函数,其中a称二次项系数,b称一次项系数,
c称常数项.特别注意:二次项系数a不能为0.2.二次函数的表达式和自变量的取值范围(2)根据实际问题列出二次函数的关系式,但要注意考
虑自变量的取值范围,自变量的取值范围应使实际问
题有意义.(1)会由x、y的3组对应值求出二次函数的表达式.练习1.下列函数表达式中,一定为二次函数的是( ) C2.已知函数y=(m2+m)x2+mx+4为二次函数,则m的取值
范围是( ) A.m≠0 B.m≠-1 C.m≠0,且m≠-1 D.m=-1C3.矩形的周长为24cm,其中一边为xcm(其中x>0),
面积为ycm2,则这样的矩形中y与x的关系可以写成
( ) A.y=x2 B.y=(12-x)x
C. y=12-x2 D.y=2(12-x)B1.2二次函数的图象1.画二次函数图象的一般步骤:①列表:列出自变量与函数的对应值;②描点:建立适当的直角坐标系,并以表中各组对应
值作为点的坐标,在直角坐标系中描出相应的点;③连线:用平滑曲线顺次连结各点.2.二次函数的图象(1)二次函数y=ax2+bx+c(a≠0)的图象是一条关于
直线 对称的抛物线,抛物线与对称轴的交点
是抛物线的顶点.(2)不同形式的二次函数图象y=ax2y=ax2+ky=a(x-h)2y=a(x-h)2+k(3)二次函数图象的平移y=ax2向上(或向下)平移 单位长度y=ax2+ky=ax2向左(或向右)y=a(x-h)2平移 单位长度y=ax2再向上(或向下)平移 单位长度y=a(x-h)2+k先向左(或向右)平移 单位长度练习1.将抛物线y=-x2向上平移2个单位后,得到的
函数表达式是( ) A.y=-x2+2 B.y=-(x+2)2
C.y=-(x-1)2 D.y=-x2-2A2.将二次函数y=-2x2的图象平移后,可得到二次函
数y=-2(x+3)2的图象,平移的方法是( ) A.向上平移3个单位 B.向下平移3个单位
C.向左平移3个单位 D.向右平移3个单位C3.将抛物线y=(x-1)2+2向上平移2个单位长度,再向右
平移3个单位长度后,得到的抛物线的解析式为( ) A.y=(x-1)2+4 B. y=(x-4)2+4
C.y=(x+2)2+6 D.y=(x-4)2+6B(5)抛物线y=ax2+bx+c(a≠0)的对称轴、顶点坐标①通过配方法将y=ax2+bx+c化成顶点式y=a(x-h)2+k;对称轴为直线x=h,顶点坐标为(h,k).②直接用公式法:对称轴为直线顶点坐标为(4)抛物线y=ax2+bx+c(a≠0)的开口方向当a>0时,抛物线开口向上,顶点是抛物线的最低点;当a<0时,抛物线开口向下,顶点是抛物线的最高点.练习1.已知二次函数y=a(x-1)2-c的图象如图所示,
则一次函数y=ax+c的大致图象可能是( )A2.把二次函数y=-2x2-4x+10,化成y=a(x-h)2+k的形式
是_______________________. y=-2(x+1)2+123.抛物线y=-x2+4x-3 的对称轴是直线__________,
顶点坐标为__________.(2,1)x=2(6)二次函数y=ax2+bx+c的系数a、b、c与图象的关系①a的符号决定抛物线的开口方向:当a>0时,抛物
线开口向上;当a<0时,抛物线开口向下,a的绝对
值决定着抛物线的形状、大小,当a的绝对值相等时,
抛物线的形状、大小相同;当a的绝对值越大时,抛
物线的开口越小.②a、b符号决定着抛物线的对称轴位置a、b同号对称轴在y轴左侧a、b异号对称轴在y轴右侧b=0对称轴是y轴③c的符号决定着抛物线与y轴的交点位置c>0与y轴交点在x轴的上方c<0c>0与y轴交点在x轴的下方抛物线必经过坐标原点已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,
对称轴是直线x=-1,下列结论: ①abc<0;②2a+b=0;
③a-b+c>0;④b2-4ac>0.其中正确的是( )A.①② B.只有①
C.③④ D.①④D练习1.3二次函数的性质1.二次函数y=ax2+bx+c(a≠0)的增减性(1)在a>0,抛物线开口向上的情况x随x的增大而增大x随x的增大而减小(2)在a<0,抛物线开口向下的情况x随x的增大而减小x随x的增大而增大说明:二次函数的增减性可结合二次函数的大致图象进行分析.1.下列函数:①y=-3x2;②y=2x2-1;③y=(x-2)2;
④y=-x2+2x+3.当x<0时,其中y随x的增大而增大的
函数有( ) 练习A.4个 B.3个 C.2个 D.1个 C3.已知二次函数y=x2+(m-1)x+1,当x>1时,y随x的
增大而增大,则m的取值范围是( )A.m=-1 B.m=3 C.m≤-1 D.m≥-12.在二次函数y=- (x-2)2+3的图象上有两点(-1,y1),
(1,y2),则y1与y2的大小关系是( )A. y1<y2 B. y1=y2 C. y1>y2 D.不能确定AD①通过配方法将y=ax2+bx+c化成顶点式y=a(x-h)2+k;若a>0,则函数y有最小值,当x=h时,y最小值=k; 若a<0,则函数y有最大值,当x=h时,y最大值=k . ②直接用公式法:2.二次函数的最大(小)值3.二次函数与一元二次方程的关系②b2-4ac的符号决定着抛物线与x轴的交点情况b2-4ac>0与x轴有两个交点b2-4ac=0与x轴有一个交点b2-4ac<0与x轴没有交点①对于二次函数y=ax2+bx+c(a≠0),如果令y=0,则ax2+bx+c=0抛物线y=ax2+bx+c与x轴的交点的横坐标即为一元二次方
程ax2+bx+c=0的两个根;一元二次方程ax2+bx+c=0的
根即为抛物线y=ax2+bx+c与x轴交点的横坐标,练习1.已知二次函数y=ax2+bx+c(a≠0)的图象如
图所示,下列说法错误的是( ) A.图象关于直线x=1对称
B.函数y=ax2+bx+c(a≠0)的
最小值是-4
C.抛物线y=ax2+bx+c(a≠0)与x轴
的两个交点的横坐标分别是-1,3
D.当x<1时,y随x的增大而增大D3.已知抛物线y=x2-(k-1)x-3k-2与x轴交于A(a,0),
B(b,0)两点,且a2+b2=17,则k的值为_______.-6或22.已知函数y=(k-3)x2+2x+1的图象与x轴有交点,则k的
取值范围是( )A.k<4 B.k≤4 C.k<4且k≠3 D.k≤4且k≠3B4.二次函数表达式的求法1.已知二次函数的图象经过点(-1,5),(0,-4)
和(1,1),则这个二次函数的表达式( )练习A.y=-6x2+3x+4 B.y=-2x2+3x-4
C.y=x2+2x-4 D.y=2x2+3x-4D3.若二次函数的图象的顶点坐标为(2,-1),抛物线
过点(0,3),则二次函数的解析式是( )4.已知二次函数的图象与x轴的两个交点A、B关于直线
x=-1对称,且AB=6,顶点在函数y=2x的图象上,
则这个二次函数的表达式为__________________. C2.顶点为(6,0),开口向下,开口的大小与函数y= x2
的图象相同的抛物线所对应的函数表达式是( ) D1.将进货单价为70元的某种商品按零售价100元/个售出
时每天能卖出20个,若这种商品的零售价在一定范围
内每降价1元,其日销售量就增加1个,为了获得最大
利润,则应降价( )1.4二次函数的应用二次函数在实际问题中的应用A.5元 B.10元 C.15元 D.20元2.某公司在甲、乙两地同时销售某种品牌的汽车.已知在
甲、乙两地的销售利润y(万元)与销售量x(辆)之间分别
满足:y1=-x2+10x,y2=2x,若该公司在甲、乙两地共
销售15辆该品牌的汽车,则能获得的最大利润是( ) A.30万元 B.40万元 C.45万元 D.46万元AD3.某商场试销一种成本为每件60元的服装,规定试销期
间销售单价不低于成本单价,且获利不得高于45%,经
试销发现,销售量y(件)与销售单价x(元)符合一次
函数y=kx+b,且x=65时,y=55;x=75时,y=45;(3)若该商场所获得利润不低于500元,试确定销售单
价x的范围.(2)若该商场获得利润为W元,试写出利润W与销售单
价x之间的关系;销售单价定为多少时,商场可获得最
大利润,最大利润是多少元?(1)求一次函数的解析式;解:(1)∵把x=65,y=55;x=75,y=45解得:∴所求一次函数的解析式为y=-x+120,(2)W=(x-60)(-x+120)
=-x2+180x-7200
=-(x-90)2+900,代入y=kx+b得:由图象可知,要使该商场获得利润不低于500元,销售
单价应在70元到110元之间,而60≤x≤87,∴当销售单价定为87元时,商场可获得最大利润,
最大利润是891元;∵抛物线的开口向下,∴当x<90时,W随x的增大而增大,又∵60≤x≤87,∴当x=87时,W=-(87-90)2+900=891,(3)由W=500,得500=-x2+180x-7200,整理得:x2-180x+7700=0,解得:x1=70,x2=110,所以,销售单价x的范围是70≤x≤87.二次函数在几何问题中的应用1.为了节省材料,某水产养殖户利用水库的岸堤(岸堤
足够长)为一边,用总长为80m的围网在水库中围成了
如图所示的①②③三块矩形区域,而且这三块矩形区
域的面积相等.设BC的长度为xm,矩形区域ABCD的
面积为ym2.(2)x为何值时,y有最大值?最大值是多少?(1)求y与x之间的函数关系式,并注明自变量x的取值范围;(1)∵三块矩形区域的面积相等, 解:∴矩形AEFD面积是矩形BCFE面积的2倍,∴AE=2BE,设BE=a,则AE=2a,∴8a+2x=80,∴a=﹣ x+10,2a=﹣ x+20,∴y=(﹣ x+20)x+(- x+10)x=﹣ x2+30x,∴x<40,则y=﹣ x2+30x(0<x<40);∵a=﹣ x+10>0,(2)∵y=﹣ x2+30x=﹣ (x﹣20)2+300(0<x<40),且二次项系数为﹣ <0,∴当x=20时,y有最大值,最大值为300平方米.3.如图,在平面直角坐标系xOy中,直线y=x-1与抛物线
C1:y=x2-2x-1相交于A、C两点,过点A作AB∥x轴
交抛物线于点B.(3)若抛物线C2:y=ax(a≠0)与线段AB恰有一个
公共点,结合函数图象,求a的取值范围.(2)求△ABC的面积;(1)求点A、C的坐标;∴S△ABC= AB×CD= ×4×3=6;(1)由解:得,∴点A、C的坐标分别为(3,2),(0,-1);(2)由题意知:点A与B关于抛物线C1的对称轴对称,∵抛物线C1的对称轴为x=1,且A(3,2),∴B(-1,2),∴AB=4,设直线AB与y轴交于点D,则CD=1+2=3,(3)如图,∴a的取值范围为 ≤a<2.把B(-1,2)代入y=ax2得:a=2,把A(3,2)代入y=ax2得:a= ,当C2过点A点,B点临界点时,再见!
同课章节目录
