1.1认识三角形(1)(浙江省温州市鹿城区)
文档属性
| 名称 | 1.1认识三角形(1)(浙江省温州市鹿城区) |

|
|
| 格式 | rar | ||
| 文件大小 | 239.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-18 00:00:00 | ||
图片预览






文档简介
课件20张PPT。我该买哪种呢?1.1 认识三角形(1) 生活离不开三角形,
那么你能否举例说明?三条线段首尾顺次相接组成的图形。不在同一条直线上的三角形:三角形的表示方法ABC“三角形”用符号“Δ”表示,如图顶点
是A,B,C的三角形记做“ΔABC”,
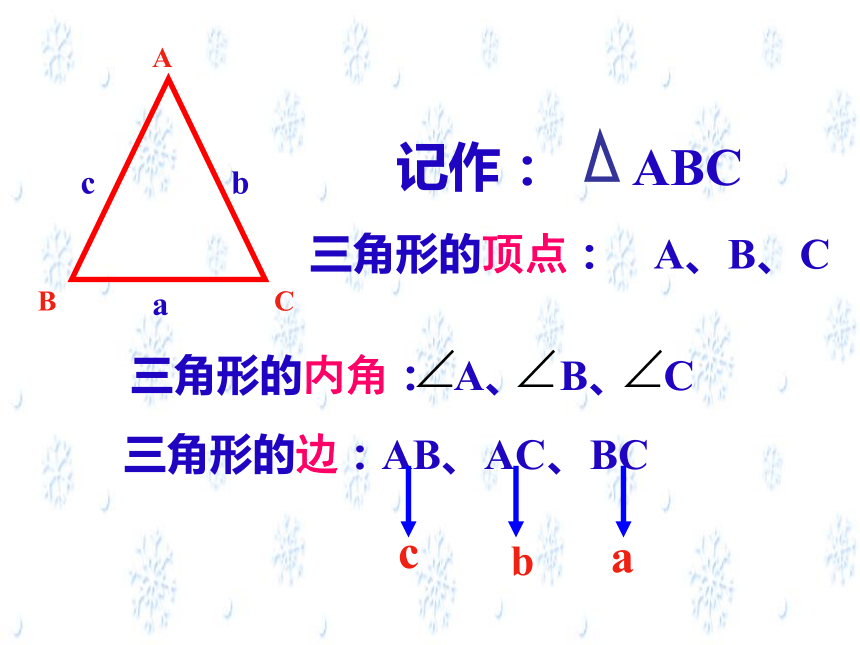
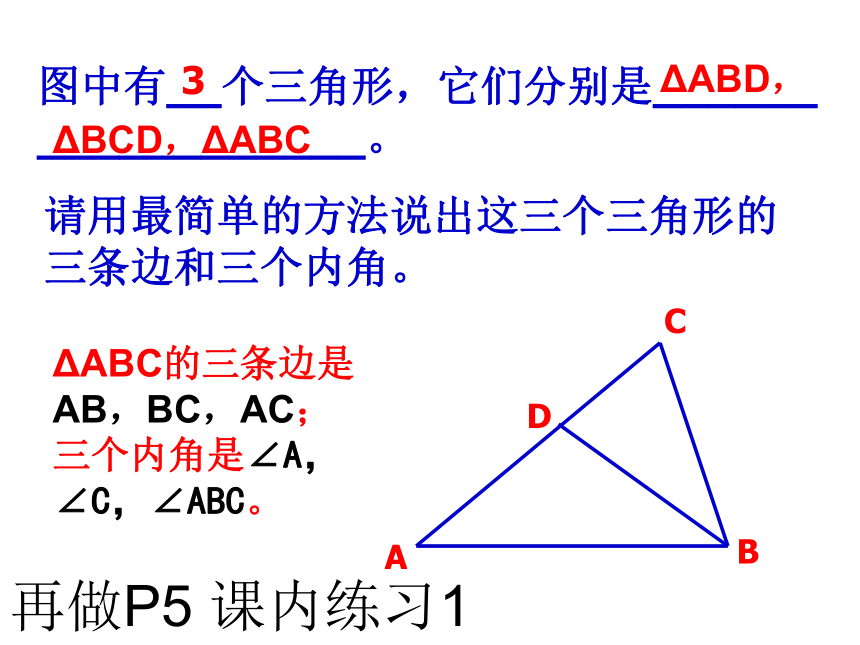
读做“三角形ABC”。ABCabc记作: ABC三角形的顶点: A、B、C三角形的边:AB、AC、BC三角形的内角: A、 B、 CcbaABCD图中有__个三角形,它们分别是______
____________。3ΔABD,ΔBCD,ΔABC请用最简单的方法说出这三个三角形的
三条边和三个内角。ΔABC的三条边是
AB,BC,AC;
三个内角是∠A,
∠C,∠ABC。再做P5 课内练习1动手实践环节:
画三角形,量边长三角形的三边
存在怎样的数量关系三角形的性质三角形任何两边的和大于第三边.ABCabca+b>ca+c>bc+b>a我们生活中很多现象都可以用数学知识来解释.人行横道.A.B两点之间线段最短.c生活中的数学 为什么有行人斜穿人行横道?家两点之间的所有连线中,线段最短三角形的三边关系:三角形的任何两边之和大于第三边a+b>cb+c>ac+a>b任何反之:在三条线段中若任两线段之和大于第三线段则这三条线段能构成一个三角形。长度为6cm, 4cm, 3cm三条线段能否组成三角形?解:∵6+4>3
6+3>4
4+3>6
∴能组成三角形这样判断需要三个条件,你一定希望有更好的判
断方法吧.想想看!解: ∵最长线段是6cm
4+3>6
∴能组成三角形学以致用判断方法:(1)找出最长线段。(2)比较大小:较短两边之和与最长线段的大小
(3)判断能否组成三角形。则不能构成三角形.例 判断下列各组线段中,哪些能组成三
角形,哪些不能组成三角形,并说明理由。
(1)a=1cm, b=2cm, c=3.5cm.
(2)e=4cm, f=5cm, g=9cm.解(1)∵ 最长线段是c=3.5cm,a+b=1+2=3(cm)∴ a+b第三边有什么关系?三角形任何两边
的差小于第三边。 3.三角形具有稳定性,并在生活中有广泛
的应用。1、三角形的三边关系: (2)已知三角形的两边,求第三边的取值范围:2.画给定边长的三角形知识梳理:任何两边的和大于第三边。两边之差?第三边?两边之和50 A.1 B.2 C.3 D.4C
那么你能否举例说明?三条线段首尾顺次相接组成的图形。不在同一条直线上的三角形:三角形的表示方法ABC“三角形”用符号“Δ”表示,如图顶点
是A,B,C的三角形记做“ΔABC”,
读做“三角形ABC”。ABCabc记作: ABC三角形的顶点: A、B、C三角形的边:AB、AC、BC三角形的内角: A、 B、 CcbaABCD图中有__个三角形,它们分别是______
____________。3ΔABD,ΔBCD,ΔABC请用最简单的方法说出这三个三角形的
三条边和三个内角。ΔABC的三条边是
AB,BC,AC;
三个内角是∠A,
∠C,∠ABC。再做P5 课内练习1动手实践环节:
画三角形,量边长三角形的三边
存在怎样的数量关系三角形的性质三角形任何两边的和大于第三边.ABCabca+b>ca+c>bc+b>a我们生活中很多现象都可以用数学知识来解释.人行横道.A.B两点之间线段最短.c生活中的数学 为什么有行人斜穿人行横道?家两点之间的所有连线中,线段最短三角形的三边关系:三角形的任何两边之和大于第三边a+b>cb+c>ac+a>b任何反之:在三条线段中若任两线段之和大于第三线段则这三条线段能构成一个三角形。长度为6cm, 4cm, 3cm三条线段能否组成三角形?解:∵6+4>3
6+3>4
4+3>6
∴能组成三角形这样判断需要三个条件,你一定希望有更好的判
断方法吧.想想看!解: ∵最长线段是6cm
4+3>6
∴能组成三角形学以致用判断方法:(1)找出最长线段。(2)比较大小:较短两边之和与最长线段的大小
(3)判断能否组成三角形。则不能构成三角形.例 判断下列各组线段中,哪些能组成三
角形,哪些不能组成三角形,并说明理由。
(1)a=1cm, b=2cm, c=3.5cm.
(2)e=4cm, f=5cm, g=9cm.解(1)∵ 最长线段是c=3.5cm,a+b=1+2=3(cm)∴ a+b
的差小于第三边。 3.三角形具有稳定性,并在生活中有广泛
的应用。1、三角形的三边关系: (2)已知三角形的两边,求第三边的取值范围:2.画给定边长的三角形知识梳理:任何两边的和大于第三边。两边之差?第三边?两边之和50
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
