5.2.2 菱形的判定 课件(共18张PPT)
文档属性
| 名称 | 5.2.2 菱形的判定 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 39.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 11:57:30 | ||
图片预览





文档简介
(共18张PPT)
菱形的判定
特殊平行四边形
学习目标
壹
经历从现实生活中抽象出图形的过程,了解菱形的概念及其与平行四边形的关系.
贰
经历利用菱形的定义探究其他判定方法的过程,培养学生的动手实验、观察、推理意识,发展学生的形象思维和逻辑推理能力.
叁
根据菱形的判定定理进行简单的证明,培养学生的逻辑推理能力和演绎能力.
肆
在探究萎形的判定方法的活动中获得成功的体验,通过运用雾形的判定和性质,锻炼克服困难的意志,建立自信心.
复习回顾
有一组邻边相等的平行四边形叫做菱形.
菱形的定义:
一组邻边相等
平行四边形
菱形
边
对角线
角
菱形的性质
菱形的两条对角线互相平分.
菱形的两组对边平行.
菱形的四条边相等.
菱形的两组对角分别相等.
菱形的邻角互补.
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角.
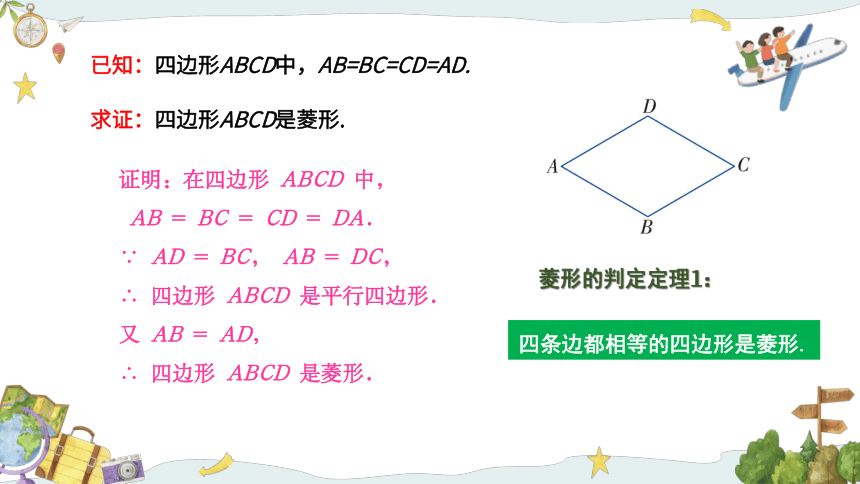
已知:四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:在四边形 ABCD 中,
AB = BC = CD = DA.
∵ AD = BC, AB = DC,
∴ 四边形 ABCD 是平行四边形.
又 AB = AD,
∴ 四边形 ABCD 是菱形.
菱形的判定定理1:
四条边都相等的四边形是菱形.
菱形的判定1
根据菱形的定义,可得菱形的第一个判定的方法.
∵AB=AD=BC=DC
∴四边形ABCD是菱形
几何语言
有四条边相等的四边形叫做菱形.
例题讲解
例1:已知:如图,在四边形 ABCD 中,线段 BD垂直平分 AC,且相交于点 O,∠1 =∠2.
求证:四边形 ABCD 是菱形.
证明 ∵线段 BD 垂直平分AC ,
∴ BA = BC,DA = DC,OA = OC.
在△AOB 和△COD 中,
∵∠1 =∠2,∠AOB =∠COD,OA = OC.
∴△OAB≌△OCD. ∴ AB = CD.
∴BA = BC = CD = DA.
∴四边形 ABCD 是菱形(四条边都相等的四边形是菱形).
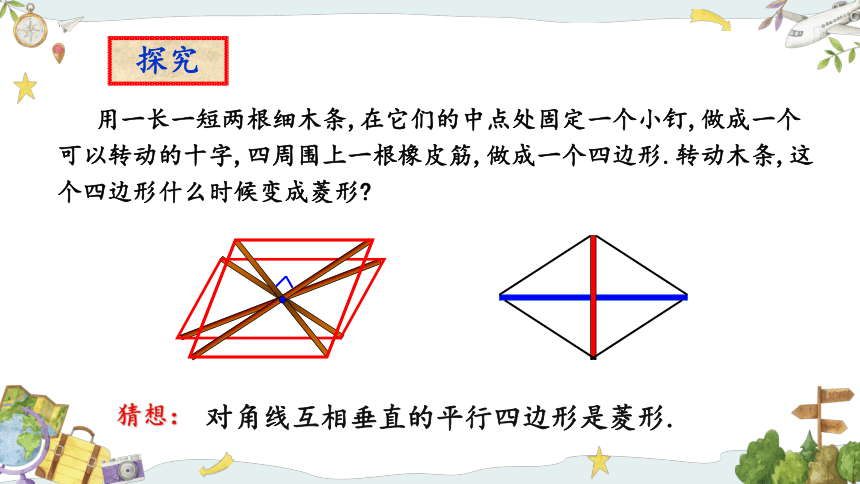
探究
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形
猜想:
对角线互相垂直的平行四边形是菱形.
已知:已知:在平行四边形ABCD中,AC ⊥ BD,
求证:四边形ABCD是菱形.
菱形的判定定理2:
证明:∵ 在 □ ABCD中,AC⊥BD,OA= OC,
∴BD 所在的直线是 AC 的垂直平分线.
∴ DA= DC.
∴ □ ABCD 是菱形.
对角线互相垂直的平行四边形是菱形.
菱形的判定2
对角线互相垂直的平行四边形是菱形.
AC⊥BD
几何语言描述:
∵在□ABCD中,AC⊥BD,
∴ □ABCD是菱形.
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
例题讲解
例2: 已知:如图,四边形ABCD是矩形,分别延长AD,CD到点E,F,使DE=AD,DF=CD,连接AC,AF,EC,EF.求证:四边形ACEF是菱形.
解 ∵ DE=AD,DF=CD,
∴ 四边形 ACEF 为平行四边形,.
∴ ∠ADC= 90°,即 AD⊥DC.
∴ □ ACEF是菱形.(对角线互相垂直的平行四边形是菱形)
又∵ 四边形ABCD是矩形,
例题讲解
例3:如图,在四边形ABCD中,AC为一条对角线,AD∥BC,AD=2BC,∠ACD=90°,
E为AD的中点,连接CE.求证:四边形ABCE 是菱形.
证明:∵E为AD的中点,AD=2BC,
∴BC=AE.
又∵AD∥BC,
∴四边形ABCE是平行四边形
又∵∠ACD=90°,E为AD的中点,
∴CE= AD=AE.
∴四边形ABCE是菱形;
笔记总结
菱形常用的判定方法:
有一组邻边相等的平行四边形叫做菱形。
对角线互相垂直的平行四边形是菱形。
有四条边相等的四边形是菱形。
+邻边相等 =
+对角线线互相垂直=
四条边相等+ =
C
A
B
D
E
F
G
H
例4: 如图,顺次连接对角线相等的四边形ABCD各边中点,得到四边形EFGH是什么四边形?
解:四边形EFGH是菱形.
又∵AC=BD,
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
【点睛】顺次连接对角线相等的四边形的各边中点,得到四边形是菱形.
理由如下:连接AC、BD
H
G
F
E
D
C
B
A
证明:连接AC、BD.
∵四边形ABCD是矩形,
∴AC=BD.
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
变式 如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.
A
B
C
D
E
F
G
H
拓展1 如图,顺次连接平行四边形ABCD各边中点,得到四边形EFGH是什么四边形?
解:连接AC、BD.
利用中位线的性质
∴四边形EFGH是平行四边形.
拓展2 若四边形ABCD是菱形,顺次连接菱形ABCD各边中点,得到四边形EFGH是什么四边形?
四边形EFGH是矩形.
∵四边形ABCD是菱形.
∴AC⊥BD .
∵四边形EFGH是平行四边形.
拓展3 若四边形ABCD是矩形,顺次连接矩形ABCD各边中点,得到四边形EFGH是什么四边形?
四边形EFGH是菱形.
∵四边形ABCD是矩形.
∴AC=BD .
∵四边形EFGH是平行四边形.
THANK YOU
感谢各位同学的观看
菱形的判定
特殊平行四边形
学习目标
壹
经历从现实生活中抽象出图形的过程,了解菱形的概念及其与平行四边形的关系.
贰
经历利用菱形的定义探究其他判定方法的过程,培养学生的动手实验、观察、推理意识,发展学生的形象思维和逻辑推理能力.
叁
根据菱形的判定定理进行简单的证明,培养学生的逻辑推理能力和演绎能力.
肆
在探究萎形的判定方法的活动中获得成功的体验,通过运用雾形的判定和性质,锻炼克服困难的意志,建立自信心.
复习回顾
有一组邻边相等的平行四边形叫做菱形.
菱形的定义:
一组邻边相等
平行四边形
菱形
边
对角线
角
菱形的性质
菱形的两条对角线互相平分.
菱形的两组对边平行.
菱形的四条边相等.
菱形的两组对角分别相等.
菱形的邻角互补.
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角.
已知:四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:在四边形 ABCD 中,
AB = BC = CD = DA.
∵ AD = BC, AB = DC,
∴ 四边形 ABCD 是平行四边形.
又 AB = AD,
∴ 四边形 ABCD 是菱形.
菱形的判定定理1:
四条边都相等的四边形是菱形.
菱形的判定1
根据菱形的定义,可得菱形的第一个判定的方法.
∵AB=AD=BC=DC
∴四边形ABCD是菱形
几何语言
有四条边相等的四边形叫做菱形.
例题讲解
例1:已知:如图,在四边形 ABCD 中,线段 BD垂直平分 AC,且相交于点 O,∠1 =∠2.
求证:四边形 ABCD 是菱形.
证明 ∵线段 BD 垂直平分AC ,
∴ BA = BC,DA = DC,OA = OC.
在△AOB 和△COD 中,
∵∠1 =∠2,∠AOB =∠COD,OA = OC.
∴△OAB≌△OCD. ∴ AB = CD.
∴BA = BC = CD = DA.
∴四边形 ABCD 是菱形(四条边都相等的四边形是菱形).
探究
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形
猜想:
对角线互相垂直的平行四边形是菱形.
已知:已知:在平行四边形ABCD中,AC ⊥ BD,
求证:四边形ABCD是菱形.
菱形的判定定理2:
证明:∵ 在 □ ABCD中,AC⊥BD,OA= OC,
∴BD 所在的直线是 AC 的垂直平分线.
∴ DA= DC.
∴ □ ABCD 是菱形.
对角线互相垂直的平行四边形是菱形.
菱形的判定2
对角线互相垂直的平行四边形是菱形.
AC⊥BD
几何语言描述:
∵在□ABCD中,AC⊥BD,
∴ □ABCD是菱形.
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
例题讲解
例2: 已知:如图,四边形ABCD是矩形,分别延长AD,CD到点E,F,使DE=AD,DF=CD,连接AC,AF,EC,EF.求证:四边形ACEF是菱形.
解 ∵ DE=AD,DF=CD,
∴ 四边形 ACEF 为平行四边形,.
∴ ∠ADC= 90°,即 AD⊥DC.
∴ □ ACEF是菱形.(对角线互相垂直的平行四边形是菱形)
又∵ 四边形ABCD是矩形,
例题讲解
例3:如图,在四边形ABCD中,AC为一条对角线,AD∥BC,AD=2BC,∠ACD=90°,
E为AD的中点,连接CE.求证:四边形ABCE 是菱形.
证明:∵E为AD的中点,AD=2BC,
∴BC=AE.
又∵AD∥BC,
∴四边形ABCE是平行四边形
又∵∠ACD=90°,E为AD的中点,
∴CE= AD=AE.
∴四边形ABCE是菱形;
笔记总结
菱形常用的判定方法:
有一组邻边相等的平行四边形叫做菱形。
对角线互相垂直的平行四边形是菱形。
有四条边相等的四边形是菱形。
+邻边相等 =
+对角线线互相垂直=
四条边相等+ =
C
A
B
D
E
F
G
H
例4: 如图,顺次连接对角线相等的四边形ABCD各边中点,得到四边形EFGH是什么四边形?
解:四边形EFGH是菱形.
又∵AC=BD,
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
【点睛】顺次连接对角线相等的四边形的各边中点,得到四边形是菱形.
理由如下:连接AC、BD
H
G
F
E
D
C
B
A
证明:连接AC、BD.
∵四边形ABCD是矩形,
∴AC=BD.
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
变式 如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.
A
B
C
D
E
F
G
H
拓展1 如图,顺次连接平行四边形ABCD各边中点,得到四边形EFGH是什么四边形?
解:连接AC、BD.
利用中位线的性质
∴四边形EFGH是平行四边形.
拓展2 若四边形ABCD是菱形,顺次连接菱形ABCD各边中点,得到四边形EFGH是什么四边形?
四边形EFGH是矩形.
∵四边形ABCD是菱形.
∴AC⊥BD .
∵四边形EFGH是平行四边形.
拓展3 若四边形ABCD是矩形,顺次连接矩形ABCD各边中点,得到四边形EFGH是什么四边形?
四边形EFGH是菱形.
∵四边形ABCD是矩形.
∴AC=BD .
∵四边形EFGH是平行四边形.
THANK YOU
感谢各位同学的观看
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
