浙教版八年级下册第五章特殊平行四边形培优练习 含解析
文档属性
| 名称 | 浙教版八年级下册第五章特殊平行四边形培优练习 含解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 483.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-22 00:00:00 | ||
图片预览




文档简介
浙教版八年级下册第五章特殊平行四边形培优练习
一、选择题
1.下列说法正确的是 ( )
A.矩形的对角线相等且互相垂直 B.菱形的对角线相等
C.正方形的对角线相等 D.菱形的四个角都是直角
2.下列条件中,能判定四边形是菱形的是( )
A.两条对角线相等 B.两条对角线互相垂直
C.两条对角线互相垂直平分 D.两条对角线相等且互相垂直
3.如图,四边形是平行四边形,下列结论中错误的是( )
A.当时,是矩形
B.当时,是菱形
C.当是正方形时,
D.当是菱形时,
4.如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是( )
A.18 B.18 C.9 D.6
5.如图,若将上图正方形剪成四块,恰能拼成下图的矩形,设,则( )
A. B. C. D.
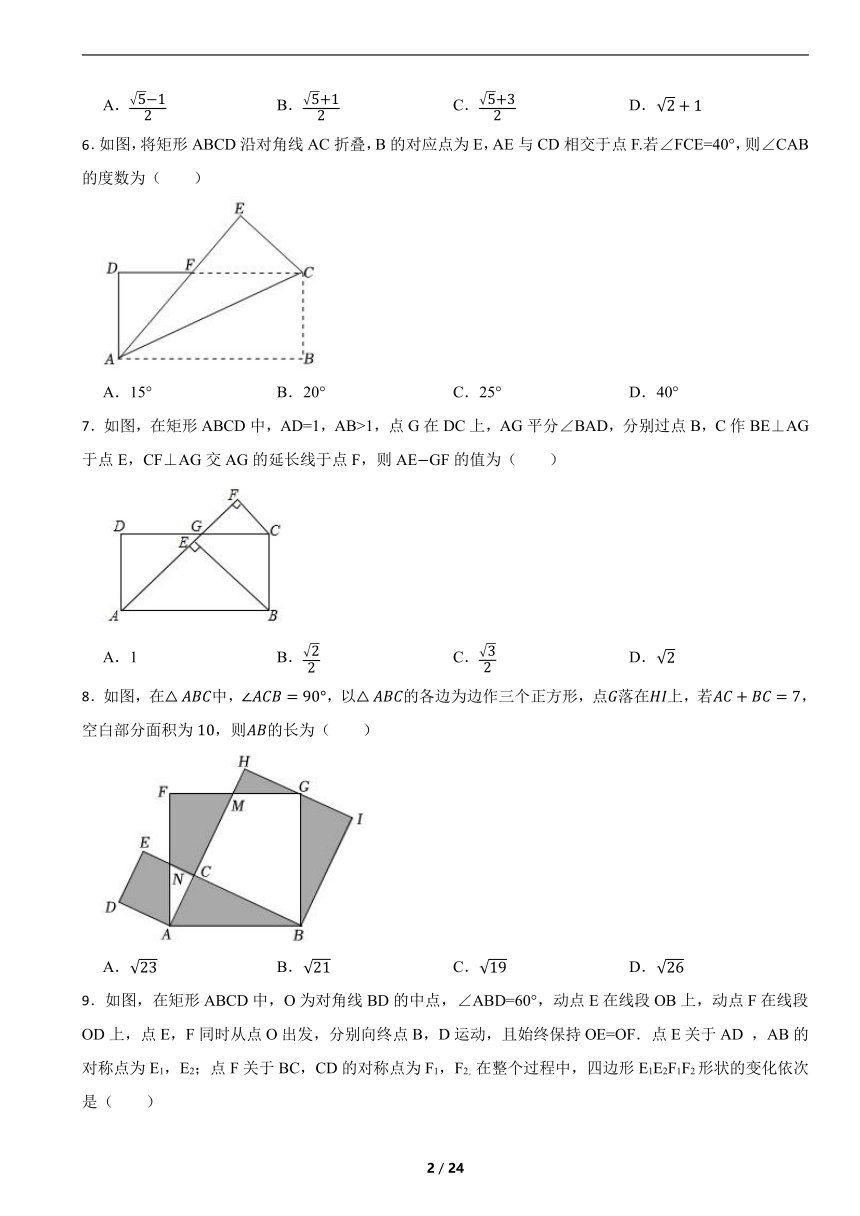
6.如图,将矩形ABCD沿对角线AC折叠,B的对应点为E,AE与CD相交于点F.若∠FCE=40°,则∠CAB的度数为( )
A.15° B.20° C.25° D.40°
7.如图,在矩形ABCD中,AD=1,AB>1,点G在DC上,AG平分∠BAD,分别过点B,C作BE⊥AG于点E,CF⊥AG交AG的延长线于点F,则AEGF的值为( )
A.1 B. C. D.
8.如图,在中,,以的各边为边作三个正方形,点落在上,若,空白部分面积为,则的长为( )
A. B. C. D.
9.如图,在矩形ABCD中,O为对角线BD的中点,∠ABD=60°,动点E在线段OB上,动点F在线段OD上,点E,F同时从点O出发,分别向终点B,D运动,且始终保持OE=OF.点E关于AD ,AB的对称点为E1,E2;点F关于BC,CD的对称点为F1,F2,在整个过程中,四边形E1E2F1F2形状的变化依次是( )
A.菱形→平行四边形→矩形→平行四边形→菱形
B.菱形→正方形→平行四边形→菱形→平行四边形
C.平行四边形→矩形→平行四边形→菱形→平行四边形
D.平行四边形→菱形→正方形→平行四边形→菱形
10.七巧板是我国祖先的一项卓越创造,如图1,正方形ABCD可以制作一副七巧板,现将这副七巧板拼成如图2所示的“风车”造型(内部有一处空缺),连结最外围的风车顶点 M,N,P,Q得到一个四边形MNPQ,则正方形ABCD与四边形MNPQ的面积之比为 ( )
A.5:8 B.3 : 5 C.8: 13 D.25:49
二、填空题
11.菱形的两条对角线的长分别为6和8,则这个菱形的周长为 .
12.如图,在菱形ABCD中,对角线 AC,BD相交于点O,不 添 加任何 辅 助线,请 添加一个条件: ,使得四边形ABCD 是正方形.
13.如图,已知ABCD中对角线AC,BD相交于点O,请你添加一个适当的条件,使ABCD成为一个矩形.你添加的条件是__.
14.如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为
15.如图①是一张等腰直角三角形纸片,,现要求按照图②的方法裁剪几条宽度都为的长方形纸条,用这些纸条为一幅正方形美术作品EFGH镶边(纸条不重叠)如图③,正方形美术作品的面积为 .
16.正方形ABCD的边长为2,如图1,点E,F均在正方形内部,且BE=EF=FD,∠E=∠F=90°,则BE的长为 ;如图2,点G,H,I,J,K,L均在正方形内部,且BG=GH=HI=IJ=JK=KL=LD,∠G=∠H=∠I=∠J=∠K=∠L=90°,则BG的长为 .
三、解答题
17.如图,是的一条角平分线,交于点E,交于点F.
(1)求证:四边形是菱形;
(2)若,当 ▲ 度时,四边形为正方形并证明.
18.如图,在正方形 ABCD中,点 E 在 BC 边的延长线上,点 F 在 CD 边的延长线上,且 CE=DF,连结 AE和BF.求证:AE=BF.
19.已知一个长方形相邻的两边长分别是a,b,且,;
(1)求此长方形的周长;
(2)若一个正方形的周长与上述长方形的周长相等,求此正方形的面积.
20.如图,在四边形ABCD中,AB∥CD,点E,F在对角线BD上,BE=EF=FD,∠BAF=∠DCE=90°.
(1)求证:△ABF≌△CDE.
(2)连结AE,CF,已知 ▲ (从条件①:∠ABD=30°.条件②:AB=BC中选择一个作为已知,填序号),请判断四边形AECF的形状,并说明理由.
21.如图,在长方形ABCD中,AD∥BC,E为边BC上一点,将长方形沿AE折叠,使点B落在点F处,EG平分∠CEF,交CD于点G,过点G作HG⊥EG,交AD于点H.
(1)试说明:HG∥AE.
(2)若∠EAF=20°,求∠DHG的度数.
22.如图,已知在正方形中,,点为线段上一点点不与、重合,连接,过点作交射线于点,以、为邻边作矩形.
(1)求证:;
(2)连接,设,的面积为求关于的函数关系式并写出自变量的取值范围;
(3)当时,求的度数.
23.如图,在平行四边形ABCD中,AD=9 cm,CD= cm,∠B=45°,点M,N分别以A,C为起点,以1 cm/s的速度沿AD,CB边运动,设点M,N运动的时间为t s(0≤t≤6). .
(1)求BC边上的高AE的长度.
(2)连结AN,CM,当t为何值时,四边形AMCN为菱形?
(3)作MP⊥BC于点P,NQ⊥AD于点Q,当t为何值时,四边形MPNQ为正方形?
24.如图1,已知O是坐标原点,点A的坐标是(5,0),B是y轴正半轴上一动点,以OB,OA为边作矩形OBCA,点E,H分别在边BC和OA上,将△BOE沿着OE对折,使点B落在OC上的点F处,将△ACH沿着CH对折,使点A落在OC上的点G处.
(1)求证:四边形OECH是平行四边形.
(2)如图2,当点F,G重合时,求点B的坐标.判断四边形OECH的形状,并说明理由.
(3)当点F,G将对角线OC三等分时,求点B的坐标.
答案解析部分
1.【答案】C
【解析】【解答】解:A、矩形的对角线相等但不互相垂直,故此选项错误;
B、菱形的对角线相互垂直,故此选项错误;
C、正方形的对角线相等且垂直,故此选项正确;
D、菱形的四个角不一定都是直角,故此选项错误.
故答案为:C.
【分析】根据矩形的对角线相等且互相平分;菱形的对角线互相平分且垂直;正方形的对角线相等、互相平分且垂直,即可逐项判断得出答案.
2.【答案】C
【解析】【解答】A、 两条对角线相等不能判定四边形是菱形,故此选项不符合题意;
B、两条对角线互相垂直不能判定四边形是菱形,故此选项不符合题意;
C、两条对角线互相垂直平分能判定四边形是菱形,故此选项符合题意;
D、两条对角线相等且互相垂直不能判定四边形是菱形,只能判定是矩形,故此选项不符合题意.
故答案为:C.
【分析】根据菱形的判定方法依次判断即可求解.
3.【答案】D
【解析】【解答】A、∵四边形是平行四边形,当时,∴是矩形,∴A正确,不符合题意;
B、∵四边形是平行四边形,当时,∴是菱形,∴B正确,不符合题意;
C、∵当是正方形时,,∴C正确,不符合题意;
D、∵当是菱形时,无法证出,∴D不正确,符合题意;
故答案为:D.
【分析】利用矩形的判定方法、菱形的判定和性质及正方形的性质逐项分析判断即可.
4.【答案】D
【解析】【解答】解:∵E为AB的中点,DE⊥AB,
∴AD=DB,
∵四边形ABCD是菱形,
∴AB=AD=DB,BD⊥AC于O
∴△ABD为等边三角形,AO=AC=3,
在Rt△AOB中,∠OAB=30°,
∴OB=
∴BD=2OB=,
∴菱形ABCD的面积=AC·BD=,
故答案为:D.
【分析】根据三角形三线合一性质可知AD=DB,再根据菱形的性质可判定出△ABD为等边三角形,∠OAB=30°,通过解含30°的直角三角形可算出BD,从而算出菱形的面积=两个对角线乘积的一半.
5.【答案】B
【解析】【解答】解:根据题意得:正方形的边长为a+b,长方形的长为a+b+b,宽为b,
则(a+b)2=b(a+b+b),即a2-b2+ab=0,
∴,
解得:,
∵>0,
∴,
∴当a=1时,,
故答案为:B.
【分析】根据题意得:正方形的边长为a+b,长方形的长为a+b+b,宽为b,则(a+b)2=b(a+b+b),即a2-b2+ab=0,可得出,根据>0,得出,当a=1时,将其代入计算即可。
6.【答案】C
【解析】【解答】解:由折叠的性质得: ∠ACE=∠ACB,
∵∠FCE=40°,∠DCB=90°,
∴∠ECB=∠FCE+∠DCB=130°,
∴,
∴∠CAB =90°-∠ACB=90°-65°=25°.
故答案为:C.
【分析】由折叠的性质及矩形的性质可得∠ECB=130°,,结合余角的性质即可得解.
7.【答案】B
【解析】【解答】解:设AE=x,
∵四边形ABCD是矩形,
∴∠BAD=∠D=90°,CD=AB,
∵AG平分∠BAD,
∴∠DAG=∠BAD=45°,
∴△DAG是等腰直角三角形,
∴DG=AD=1,
,
同理可证AE=BE,FG=CF,
∴AE=BE=x,则,
,,
∴
故答案为:B.
【分析】设AE=x,利用矩形的性质可证得∠BAD=∠D=90°,CD=AB,利用角平分线的定义可证得△DAG是等腰直角三角形,利用勾股定理求出AG的长,同理可证AE=BE,FG=CF,AE=BE=x,可表示出CD的长,同时可得到CG,FG的长,然后可求出AE-FG的长.
8.【答案】A
【解析】【解答】解:四边形是正方形,
,,
,
,
,
,
,,
≌,
的面积的面积,
四边形FNCM的面积=△ABC的面积,
空白部分的面积正方形的面积的面积,
,
,
,
,
,
,
由①×+②得,
(舍去负值).
故答案为:A.
【分析】由正方形的性质得AB=AF,∠BAN=∠F=90°,由同角的余角相等得∠ABN=∠MAF,从而根据ASA判断出△BAN≌△AFM,得S△BAN=S△AFM,推出S四边形FNCM=S△ABC,S空白部分=S正方形ABGF-2S△ABC,据此得AB2-2×AC×BC=10①,由AC+BC=7并结合勾股定理可得AB2+2AC×BC=49②,①×2+②可得AB2=23,再求其算术平方根即可.
9.【答案】A
【解析】【解答】解:如图1:
∵四边形ABCD是矩形,
∴AB∥CD,∠BAD=∠ABC=90°,
∴∠BDC=∠ABD=60°,∠ADB=∠CBD=90°-60°=30°,
∵OE=OF,OB=OD,
∴DF=EB,
∵点E关于AD ,AB的对称点为E1,E2;点F关于BC,CD的对称点为F1,F2 ,
∴DF=DF2,BF=BF1,BE=BE2,DE=DE1,E1F2=E2F1.
∴∠F2DC=∠BDC=60°,∠E1DA=∠ADB=30°,
∴∠E1DB=60°,
同理∠F1BD=60°,
∴DE1∥BF1,
∴四边形 E1E2F1F2 是平行四边形,
如图2所示,当E,F,O三点重合时,DO=OB,
∴DE1=DF2=AE1=AE2,即E1E2=E1F2,
∴四边形E1E2F1F2 是菱形.
如图3所示,当E,F分别为OD,OB的中点时,设DB=4,则 DF2=DF=1,DE1=DE=3,
在Rt△ABD中,AB=2,AD=,连接AE,AO,
∵∠ABO=60°,BO=2=AB,
∴△ABO是等边三角形,
∵E为OB中点,
∴AE⊥OB,BE=1,
∴∠E1=90°,
即四边形E1E2F1F2 是矩形.
当F,E分别与D,B重合时,△BE1D,△BDF1 都是等边三角形,则四边形E1E2F1F2 是菱形,
∴在整个过程中,四边形 E1E2F1F2 形状的变化依次是菱形→平行四边形→矩形→平行四边形→菱形,
故答案为:A.
【分析】E、F在特殊点时需分析四边形E1E2F1F2 的形状,而在一般点时均是平行四边形,根据对称的形式,菱形、平行四边形和矩形的判定方法判断即可.
10.【答案】C
【解析】【解答】解:如图1,设AC=4a,则AB=BC=AC=a,
∴正方形ABCD的面积为AB2=8a2,
由图1可得ME=QF=PG=NH,QE=PF=NG=MH,∠QFP=∠PGN=∠NHM=∠MEQ=135°,
∴△QFP≌△PGN≌△NHM≌△MEQ(SAS)
∴QM=QP=PN=MN,∠PQF=∠GPN,
∴∠NPQ=∠GPN+∠FPQ+∠FPG=∠PQF+∠FPQ+∠FPG=45°+45°=90°,
∴四边形MNPQ为正方形,
由AC=4a,则图2中MH=3a,QH=2a
∴MQ2=MH2+QH2=(3a)2+(2a)2=13a2,
∴ 四边形MNPQ的面积= MQ2=13a2,
∴ 正方形ABCD与四边形MNPQ的面积之比=8a2:13a2=8∶13.
故答案为:C.
【分析】设AC=4a,则AB=BC=AC=a,图2中MH=3a,QH=2a,由勾股定理求出MQ2,分别求出两正方形的面积公式,继而求出比值.
11.【答案】20
【解析】【解答】解:如图,根据题意得AO= ×8=4,BO= ×6=3,
∵四边形ABCD是菱形,∴AB=BC=CD=DA,AC⊥BD.
∴△AOB是直角三角形.
∴ .
∴此菱形的周长为:5×4=20
故答案为:20.
【分析】根据菱形的对角线互相垂直平分的性质,利用对角线的一半,根据勾股定理求出菱形的边长,再根据菱形的四条边相等求出周长即可.
12.【答案】∠BAD=90°(答案不唯一)
【解析】【解答】解:∵四边形ABCD是菱形,
∴当∠BAD=90°或BD=AC时, 四边形ABCD是正方形.
故答案为:∠BAD=90°(答案不唯一).
【分析】有一个角是直角的菱形是正方形,对角线相等的菱形是正方形,据此解答即可.
13.【答案】AC=BD(答案不唯一)
【解析】【解答】解:添加的条件是AC =BD(答案不唯一),
理由如下:∵AC=BD,四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形,
故答案为:AC = BD(答案不唯一).
【分析】利用矩形的判定方法证明即可。
14.【答案】
【解析】【解答】解:如图,连接、,
点、分别是、的中点,
,
正方形的边长为2,
,
点是边长的动点,
,
,
的最大值为.
故答案为:.
【分析】由点E是BC边长的动点可得,利用正方形的性质求得AC的边长,进而得到AE的取值范围,再通过三角形的中位线定理求得MN的最大值.
15.【答案】
【解析】【解答】解:如图,
∵△ABC是等腰直角三角形,且AC=BC,
∴∠B=∠C=45°,
∵四边形CDHG是矩形,且CD= ,
∴HG=CD= ,∠BGH=90°,
∴∠B=∠BHG=45°,
∴GB=GH=,
∴CG=DH=BC-BG=cm,
∵四边形CDHG是矩形,
∴DH∥BC,
∴∠B=∠DHN=45°,
∵四边形DENM是矩形,且DE=,
∴MN=ED= ,∠NMH=90°,
∴∠MNH=∠MHN=45°,
∴MN=MH=,
∴DM=EN=DN-MH=cm;
同理FQ=PE=,
∵AF=AC-CD-DE-EF=,
∴这样的长方形纸条只能裁出三条,
这三条的总长度为:CG+DM+EN=cm,
∴美术作品的边长为:cm,
∴这个美术作品的面积为:cm2.
故答案为:.
【分析】由等腰直角三角形的性质得∠B=∠C=45°,由矩形的性质得HG=CD= ,∠BGH=90°,从而可推出△BHG是等腰直角三角形,得GB=GH=,CG=DH=BC-BG=cm,同理可求出DM、PE得长,可得到裁剪出的矩形纸条的总长度,进而结合图③找出美术作品的边长,最后根据正方形面积计算方法计算可得答案.
16.【答案】;
【解析】【解答】解:连接BD,交BD于点M,
在△DFM和△BEM中
∴△DFM≌△BEM(AAS),
∴BM=DM,FM=ME,
∵正方形ABCD,
∴∠A=90°,AB=AD=2,
∴,
∴,
设ME=x,则BE=2x,
∴BE2+ME2=BM2即x2+4x2=2,
解之:x=,
∴;
如图,将KL,HJ,HI,HG平移,
设BG=GH=HI=IJ=JK=KL=LD=x,可知DS=2x, SO=1.5x,
∴(1.5x)2+(2x)2=2
解之:x=.
故答案为:,.
【分析】连接BD,交BD于点M,利用AAS证明△DFM≌△BEM,利用全等三角形的性质可证得BM=DM,FM=ME,利用正方形的性质可得到∠A=90°,AB=AD=2,利用勾股定理求出BD的长,可得到BM的长;设ME=x,则BE=2x,利用勾股定理可得到关于x的方程,解方程求出x的值,可得到BE的长;如图,将KL,HJ,HI,HG平移,设BG=GH=HI=IJ=JK=KL=LD=x,则DS=2x, SO=1.5x,利用勾股定理可得到关于x的方程,解方程求出x的值,即可求解.
17.【答案】(1)证明:∵交于点E,交于点F.
∴四边形AEDF是平行四边形,∠EAD=∠ADF,
∵是的一条角平分线,
∴∠EAD=∠FAD,
∴∠ADF=∠FAD,
∴FA=FD,
∴四边形AEDF是菱形;
(2)解:当△ABC是直角三角形,∠BAC=90°,此时∠C=55°,四边形AEDF是正方形,
理由:∵△ABC是直角三角形,∠BAC=90°,
由(1)可得四边形AEDF是菱形,
∴四边形AEDF是正方形,
∵∠B=35°,∠BAC=90°,
∴∠C=55°,
故答案为:55°.
【解析】【分析】(1)先利用角平分线的定义及等量代换可得∠ADF=∠FAD,利用等角对等边的性质可得FA=FD,再结合四边形AEDF是平行四边形,可得四边形AEDF是菱形;
(2)根据△ABC是直角三角形,∠BAC=90°,四边形AEDF是菱形,可得四边形AEDF是正方形,再结合∠B=35°,∠BAC=90°,求出∠C=55°即可.
18.【答案】证明:∵ 四边形ABCD为正方形,
∴ AB=BC=BC=CD,∠ABE=∠BCF=90°,
∵ CE=DF,
∴ BC+CE=CD+DF,即BE=CF,
∴ △ABE≌△BCF(SAS),
∴ AE=BF.
【解析】【分析】根据正方形的性质得AB=BC=BC=CD,∠ABE=∠BCF=90°,推出BE=CF,依据SAS判定△ABE≌△BCF,根据全等三角形的对应边相等即可求得.
19.【答案】(1)解:长方形的周长为
(2)解:正方形的周长为,
∴正方形的边长为,∴正方形的面积为
【解析】【分析】(1)直接根据长方形的周长公式进行求解即可;
(2)根据正方形与长方形的周长相等求得正方形的边长,再利用正方形的面积公式进行计算即可求解.
20.【答案】(1)证明:∵AB∥CD,
∴∠ABF=∠CDE,
∵ BE=EF=FD,
∴BF=DE,
在△ABF和△CDE中
∴ △ABF≌△CDE(AAS)
(2)解:①或②,四边形 AECF 是菱形,
如图,
已知①即 ∠ABD=30° ,
理由:
∵△ABF≌△CDE,
∴AF=CE,∠AFB=∠CED
∴AF∥CE,
∴四边形AECF是平行四边形,
∵∠ABD=30°,∠BAF=90°,BE=EF,
∴AE=BF,AF=BF,
∴AE=AF,
∴四边形AECF是菱形;
【解析】【分析】(1)利用平行线的性质可证得∠ABF=∠CDE,利用已知可得到BF=DE,再利用AAS可证得结论.
(2)已知①即 ∠ABD=30° ,利用全等三角形的性质及平行线的性质可证得AF=CE,AF∥CE,由此可推出四边形AECF是平行四边形;再利用直角三角形斜边上的中线等于斜边的一半和30°角所对的直角边等于斜边的一半去证明AE=AF,据此可证得四边形AECF是菱形.
21.【答案】(1)证明:由折叠得:
∵EG平分∠CEF,
∴
∴
∵
∴
∴.
(2)解:∵四边形ABCD为长方形,
∴
由折叠得:
∴
∵AD∥BC,
∴
∵,
∴.
【解析】【分析】(1)由折叠得∠AEB=∠AEF,然后根据角平分线的定义和平角的定义即可得∠AEG=90°,结合题目已给信息,由同旁内角互补,两直线平行可证HG∥AE;
(2)根据矩形的性质得到∠B=90°,AD∥BC,然后根据折叠的性质和三角形内角和定理即可求出∠BEA的度数,进而由二直线平行,内错角相等得到∠DAE的度数,最后根据二直线平行,同位角相等即可求解.
22.【答案】(1)证明:如图,作,.
,,
四边形是正方形,
,
四边形是矩形,
,
点是正方形对角线上的点,
,
四边形是矩形,
,
,
在和中,
,
≌,
;
(2)解:四边形是矩形,,
矩形是正方形,
,,
四边形是正方形,
,,,
,
≌,
,,
,
,
,,
,
的面积
(3)解:如图,当点在线段上时,
四边形是正方形,
,
,,
;
如图,当点在线段的延长线上时,
,,
,
综上,的度数为或.
【解析】【分析】本题主要考查正方形的基本性质、矩形的判定和性质、三角形全等的判定及性质.
(1)作,,结合题意可证得四边形是矩形,然后运用矩形和正方形的性质可得到≌,进而得到答案;
(2)根据矩形和正方形的性质运用等量代换的方法可证得:≌,得到,进而表示出的面积y的表达式;
(3)分点在线段上和点在线段的延长线上两种情况进行求解即可.
23.【答案】(1)解:∵四边形ABCD是平行四边形,∴AB= CD=3cm, 在Rt△ABE中,∠AEB=90 ,∠B=45°,∴设BE=AE=xcm,则有x2+x2 =(3)2,解得x=3,即AE的长度为3cm.
(2)解:∵点M,N分别以A,C为起点,以1 cm/s的速度沿AD,CB边运动,设点M,N运动的时间为t s(0≤t≤6),
∴AM=CN=t cm.∵AM∥ CN,∴四边形AMCN为平行四边形,
∴当AN=AM时,四边形AMCN为菱形.
∵BE=AE=3 cm,EN=(6-t)cm,∴AN2=32+(6-t)2,
∴32+(6-t)2=t2 ,解得t=
故当t为时,四边形AMCN为菱形.
(3)解:∵MP⊥BC于点P,NQ⊥AD于点Q,QM∥NP,∴四边形MPNQ
为矩形,∴当QM=QN时,四边形MPNQ为正方形.∵AM=CN=tcm,
BE=3 cm,∴AQ=EN=BC -BE -CN=9-3-t=(6-t)cm,
∴QM=|AM-AQ|=|t-(6-t)|=、2t-6|(注:分点Q在点M的左右两种情况).
∵QN=AE=3 cm,∴|2t-6|=3,解得t=4.5 或t=1.5.
故当t为4.5或1.5时,四边形MPNQ为正方形.
【解析】【分析】(1)根据勾股定理,列算式解答即可;
(2)根据菱形的判定方法,邻边相等的平行四边形为菱形,结合勾股定理,可解答;
(3)根据正方形的判定方法,邻边相等的矩形为正方形,再结合勾股定理可解答,但需要分Q在点M的左右两种情况,所以列式时需加上绝对值.
24.【答案】(1)证明:∵四边形OBCA为矩形,
∴OB//CA,BC//OA,
∴∠BOC=∠OCA,
由折叠的性质可得:∠BOC=2∠EOC,∠OCA=2∠OCH,
∴∠EOC=∠OCH,
∴OE//CH,
又∵BC//OA,
∴四边形OECH是平行四边形;
(2)解:四边形OECH是菱形.理由如下:
由折叠的性质可得∠EFO=∠EBO=90°,∠CFH=∠CAF=90°,
∵点F,G重合,
∴EH⊥OC,
又∵四边形OECH是平行四边形,
∴平行四边形OECH是菱形,
∴EO=EC,
∴∠EOC=∠ECO,
又∵∠EOC=∠BOE,
∴∠EOB=∠EOC=∠ECO=30°,
点A的坐标是(5,0),
∴OA=5,
由直角三角形的性质可得:OB=
∴点B的坐标是(0,);
(3)解:当点F在点O,G之间时,如图3,
由折叠性质得:OF=OB,CG=CA,
而OB=CA,
∴OF=CG,
∵点F,G将对角线OC三等分,
∴AC=OF=FG=GC,
设AC=m,则OC=3m,
在Rt△OAC中,OA=5,
由勾股定理得:AC2+OA2=OC2,
即:m2+52=(3m)2,解得m=,
∴OB=AC=,
∴点B的坐标是(0,);
当点G在O,F之间时,如图4,
同理可得OF=CG=AC,
设OG=n,则AC=GC=2n,
在Rt△OAC中,OA=5,
由勾股定理得:AC2+OA2=OC2,
即:(2n)2+52=(3n)2,解得n=,
∴AC=OB=2,
∴点B的坐标是(0,2).
故B的坐标是(0,)或(0,2).
【解析】【分析】(1)根据矩形的性质得OB∥CA,BC∥OA,再利用平行线的性质得∠BOC=∠OCA,然后根据折叠的性质得到∠BOC=2∠EOC,∠OCA=2∠OCH,所以∠EOC=∠OCH,根据平行线的判定定理得OE∥CH,根据平行四边形的判定方法:两组对边分别平行的四边形是平行四边形,即可得证;
(2)先根据折叠的性质得∠EFO=∠EBO=90°,∠CFH=∠CAF=90°,由点F,G重合得到EH⊥OC,根据菱形的判定方法:对角线垂直的平行四边形是菱形,得到四边形OECH是菱形,则EO=EC,所以∠EOC=∠ECO,而∠EOC=∠BOE,根据三角形内角和定理可计算出∠EOB=∠EOC=∠ECO=30°,在Rt△OBC中,根据含30度的直角三角形三边的关系得OB=,于是得到点B的坐标是(0,);
(3)分类讨论:当点F在点O,G之间时,如图3,根据折叠的性质得OF=OB,CG=CA,则OF=CG,所以AC=OF=FG=GC,设AC=m,则OC=3m,在Rt△OAC中,根据勾股定理得m2+52=(3m)2,解得m=,则点B的坐标是(0,);当点G在O,F之间时,如图4,同理可得OF=CG=AC,设OG=n,则AC=GC=2n,在Rt△OAC中,根据勾股定理得(2n)2+52=(3n)2,解得n=,则AC=OB=2,所以点B的坐标是(0,2),即可得解.
1 / 1
一、选择题
1.下列说法正确的是 ( )
A.矩形的对角线相等且互相垂直 B.菱形的对角线相等
C.正方形的对角线相等 D.菱形的四个角都是直角
2.下列条件中,能判定四边形是菱形的是( )
A.两条对角线相等 B.两条对角线互相垂直
C.两条对角线互相垂直平分 D.两条对角线相等且互相垂直
3.如图,四边形是平行四边形,下列结论中错误的是( )
A.当时,是矩形
B.当时,是菱形
C.当是正方形时,
D.当是菱形时,
4.如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是( )
A.18 B.18 C.9 D.6
5.如图,若将上图正方形剪成四块,恰能拼成下图的矩形,设,则( )
A. B. C. D.
6.如图,将矩形ABCD沿对角线AC折叠,B的对应点为E,AE与CD相交于点F.若∠FCE=40°,则∠CAB的度数为( )
A.15° B.20° C.25° D.40°
7.如图,在矩形ABCD中,AD=1,AB>1,点G在DC上,AG平分∠BAD,分别过点B,C作BE⊥AG于点E,CF⊥AG交AG的延长线于点F,则AEGF的值为( )
A.1 B. C. D.
8.如图,在中,,以的各边为边作三个正方形,点落在上,若,空白部分面积为,则的长为( )
A. B. C. D.
9.如图,在矩形ABCD中,O为对角线BD的中点,∠ABD=60°,动点E在线段OB上,动点F在线段OD上,点E,F同时从点O出发,分别向终点B,D运动,且始终保持OE=OF.点E关于AD ,AB的对称点为E1,E2;点F关于BC,CD的对称点为F1,F2,在整个过程中,四边形E1E2F1F2形状的变化依次是( )
A.菱形→平行四边形→矩形→平行四边形→菱形
B.菱形→正方形→平行四边形→菱形→平行四边形
C.平行四边形→矩形→平行四边形→菱形→平行四边形
D.平行四边形→菱形→正方形→平行四边形→菱形
10.七巧板是我国祖先的一项卓越创造,如图1,正方形ABCD可以制作一副七巧板,现将这副七巧板拼成如图2所示的“风车”造型(内部有一处空缺),连结最外围的风车顶点 M,N,P,Q得到一个四边形MNPQ,则正方形ABCD与四边形MNPQ的面积之比为 ( )
A.5:8 B.3 : 5 C.8: 13 D.25:49
二、填空题
11.菱形的两条对角线的长分别为6和8,则这个菱形的周长为 .
12.如图,在菱形ABCD中,对角线 AC,BD相交于点O,不 添 加任何 辅 助线,请 添加一个条件: ,使得四边形ABCD 是正方形.
13.如图,已知ABCD中对角线AC,BD相交于点O,请你添加一个适当的条件,使ABCD成为一个矩形.你添加的条件是__.
14.如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为
15.如图①是一张等腰直角三角形纸片,,现要求按照图②的方法裁剪几条宽度都为的长方形纸条,用这些纸条为一幅正方形美术作品EFGH镶边(纸条不重叠)如图③,正方形美术作品的面积为 .
16.正方形ABCD的边长为2,如图1,点E,F均在正方形内部,且BE=EF=FD,∠E=∠F=90°,则BE的长为 ;如图2,点G,H,I,J,K,L均在正方形内部,且BG=GH=HI=IJ=JK=KL=LD,∠G=∠H=∠I=∠J=∠K=∠L=90°,则BG的长为 .
三、解答题
17.如图,是的一条角平分线,交于点E,交于点F.
(1)求证:四边形是菱形;
(2)若,当 ▲ 度时,四边形为正方形并证明.
18.如图,在正方形 ABCD中,点 E 在 BC 边的延长线上,点 F 在 CD 边的延长线上,且 CE=DF,连结 AE和BF.求证:AE=BF.
19.已知一个长方形相邻的两边长分别是a,b,且,;
(1)求此长方形的周长;
(2)若一个正方形的周长与上述长方形的周长相等,求此正方形的面积.
20.如图,在四边形ABCD中,AB∥CD,点E,F在对角线BD上,BE=EF=FD,∠BAF=∠DCE=90°.
(1)求证:△ABF≌△CDE.
(2)连结AE,CF,已知 ▲ (从条件①:∠ABD=30°.条件②:AB=BC中选择一个作为已知,填序号),请判断四边形AECF的形状,并说明理由.
21.如图,在长方形ABCD中,AD∥BC,E为边BC上一点,将长方形沿AE折叠,使点B落在点F处,EG平分∠CEF,交CD于点G,过点G作HG⊥EG,交AD于点H.
(1)试说明:HG∥AE.
(2)若∠EAF=20°,求∠DHG的度数.
22.如图,已知在正方形中,,点为线段上一点点不与、重合,连接,过点作交射线于点,以、为邻边作矩形.
(1)求证:;
(2)连接,设,的面积为求关于的函数关系式并写出自变量的取值范围;
(3)当时,求的度数.
23.如图,在平行四边形ABCD中,AD=9 cm,CD= cm,∠B=45°,点M,N分别以A,C为起点,以1 cm/s的速度沿AD,CB边运动,设点M,N运动的时间为t s(0≤t≤6). .
(1)求BC边上的高AE的长度.
(2)连结AN,CM,当t为何值时,四边形AMCN为菱形?
(3)作MP⊥BC于点P,NQ⊥AD于点Q,当t为何值时,四边形MPNQ为正方形?
24.如图1,已知O是坐标原点,点A的坐标是(5,0),B是y轴正半轴上一动点,以OB,OA为边作矩形OBCA,点E,H分别在边BC和OA上,将△BOE沿着OE对折,使点B落在OC上的点F处,将△ACH沿着CH对折,使点A落在OC上的点G处.
(1)求证:四边形OECH是平行四边形.
(2)如图2,当点F,G重合时,求点B的坐标.判断四边形OECH的形状,并说明理由.
(3)当点F,G将对角线OC三等分时,求点B的坐标.
答案解析部分
1.【答案】C
【解析】【解答】解:A、矩形的对角线相等但不互相垂直,故此选项错误;
B、菱形的对角线相互垂直,故此选项错误;
C、正方形的对角线相等且垂直,故此选项正确;
D、菱形的四个角不一定都是直角,故此选项错误.
故答案为:C.
【分析】根据矩形的对角线相等且互相平分;菱形的对角线互相平分且垂直;正方形的对角线相等、互相平分且垂直,即可逐项判断得出答案.
2.【答案】C
【解析】【解答】A、 两条对角线相等不能判定四边形是菱形,故此选项不符合题意;
B、两条对角线互相垂直不能判定四边形是菱形,故此选项不符合题意;
C、两条对角线互相垂直平分能判定四边形是菱形,故此选项符合题意;
D、两条对角线相等且互相垂直不能判定四边形是菱形,只能判定是矩形,故此选项不符合题意.
故答案为:C.
【分析】根据菱形的判定方法依次判断即可求解.
3.【答案】D
【解析】【解答】A、∵四边形是平行四边形,当时,∴是矩形,∴A正确,不符合题意;
B、∵四边形是平行四边形,当时,∴是菱形,∴B正确,不符合题意;
C、∵当是正方形时,,∴C正确,不符合题意;
D、∵当是菱形时,无法证出,∴D不正确,符合题意;
故答案为:D.
【分析】利用矩形的判定方法、菱形的判定和性质及正方形的性质逐项分析判断即可.
4.【答案】D
【解析】【解答】解:∵E为AB的中点,DE⊥AB,
∴AD=DB,
∵四边形ABCD是菱形,
∴AB=AD=DB,BD⊥AC于O
∴△ABD为等边三角形,AO=AC=3,
在Rt△AOB中,∠OAB=30°,
∴OB=
∴BD=2OB=,
∴菱形ABCD的面积=AC·BD=,
故答案为:D.
【分析】根据三角形三线合一性质可知AD=DB,再根据菱形的性质可判定出△ABD为等边三角形,∠OAB=30°,通过解含30°的直角三角形可算出BD,从而算出菱形的面积=两个对角线乘积的一半.
5.【答案】B
【解析】【解答】解:根据题意得:正方形的边长为a+b,长方形的长为a+b+b,宽为b,
则(a+b)2=b(a+b+b),即a2-b2+ab=0,
∴,
解得:,
∵>0,
∴,
∴当a=1时,,
故答案为:B.
【分析】根据题意得:正方形的边长为a+b,长方形的长为a+b+b,宽为b,则(a+b)2=b(a+b+b),即a2-b2+ab=0,可得出,根据>0,得出,当a=1时,将其代入计算即可。
6.【答案】C
【解析】【解答】解:由折叠的性质得: ∠ACE=∠ACB,
∵∠FCE=40°,∠DCB=90°,
∴∠ECB=∠FCE+∠DCB=130°,
∴,
∴∠CAB =90°-∠ACB=90°-65°=25°.
故答案为:C.
【分析】由折叠的性质及矩形的性质可得∠ECB=130°,,结合余角的性质即可得解.
7.【答案】B
【解析】【解答】解:设AE=x,
∵四边形ABCD是矩形,
∴∠BAD=∠D=90°,CD=AB,
∵AG平分∠BAD,
∴∠DAG=∠BAD=45°,
∴△DAG是等腰直角三角形,
∴DG=AD=1,
,
同理可证AE=BE,FG=CF,
∴AE=BE=x,则,
,,
∴
故答案为:B.
【分析】设AE=x,利用矩形的性质可证得∠BAD=∠D=90°,CD=AB,利用角平分线的定义可证得△DAG是等腰直角三角形,利用勾股定理求出AG的长,同理可证AE=BE,FG=CF,AE=BE=x,可表示出CD的长,同时可得到CG,FG的长,然后可求出AE-FG的长.
8.【答案】A
【解析】【解答】解:四边形是正方形,
,,
,
,
,
,
,,
≌,
的面积的面积,
四边形FNCM的面积=△ABC的面积,
空白部分的面积正方形的面积的面积,
,
,
,
,
,
,
由①×+②得,
(舍去负值).
故答案为:A.
【分析】由正方形的性质得AB=AF,∠BAN=∠F=90°,由同角的余角相等得∠ABN=∠MAF,从而根据ASA判断出△BAN≌△AFM,得S△BAN=S△AFM,推出S四边形FNCM=S△ABC,S空白部分=S正方形ABGF-2S△ABC,据此得AB2-2×AC×BC=10①,由AC+BC=7并结合勾股定理可得AB2+2AC×BC=49②,①×2+②可得AB2=23,再求其算术平方根即可.
9.【答案】A
【解析】【解答】解:如图1:
∵四边形ABCD是矩形,
∴AB∥CD,∠BAD=∠ABC=90°,
∴∠BDC=∠ABD=60°,∠ADB=∠CBD=90°-60°=30°,
∵OE=OF,OB=OD,
∴DF=EB,
∵点E关于AD ,AB的对称点为E1,E2;点F关于BC,CD的对称点为F1,F2 ,
∴DF=DF2,BF=BF1,BE=BE2,DE=DE1,E1F2=E2F1.
∴∠F2DC=∠BDC=60°,∠E1DA=∠ADB=30°,
∴∠E1DB=60°,
同理∠F1BD=60°,
∴DE1∥BF1,
∴四边形 E1E2F1F2 是平行四边形,
如图2所示,当E,F,O三点重合时,DO=OB,
∴DE1=DF2=AE1=AE2,即E1E2=E1F2,
∴四边形E1E2F1F2 是菱形.
如图3所示,当E,F分别为OD,OB的中点时,设DB=4,则 DF2=DF=1,DE1=DE=3,
在Rt△ABD中,AB=2,AD=,连接AE,AO,
∵∠ABO=60°,BO=2=AB,
∴△ABO是等边三角形,
∵E为OB中点,
∴AE⊥OB,BE=1,
∴∠E1=90°,
即四边形E1E2F1F2 是矩形.
当F,E分别与D,B重合时,△BE1D,△BDF1 都是等边三角形,则四边形E1E2F1F2 是菱形,
∴在整个过程中,四边形 E1E2F1F2 形状的变化依次是菱形→平行四边形→矩形→平行四边形→菱形,
故答案为:A.
【分析】E、F在特殊点时需分析四边形E1E2F1F2 的形状,而在一般点时均是平行四边形,根据对称的形式,菱形、平行四边形和矩形的判定方法判断即可.
10.【答案】C
【解析】【解答】解:如图1,设AC=4a,则AB=BC=AC=a,
∴正方形ABCD的面积为AB2=8a2,
由图1可得ME=QF=PG=NH,QE=PF=NG=MH,∠QFP=∠PGN=∠NHM=∠MEQ=135°,
∴△QFP≌△PGN≌△NHM≌△MEQ(SAS)
∴QM=QP=PN=MN,∠PQF=∠GPN,
∴∠NPQ=∠GPN+∠FPQ+∠FPG=∠PQF+∠FPQ+∠FPG=45°+45°=90°,
∴四边形MNPQ为正方形,
由AC=4a,则图2中MH=3a,QH=2a
∴MQ2=MH2+QH2=(3a)2+(2a)2=13a2,
∴ 四边形MNPQ的面积= MQ2=13a2,
∴ 正方形ABCD与四边形MNPQ的面积之比=8a2:13a2=8∶13.
故答案为:C.
【分析】设AC=4a,则AB=BC=AC=a,图2中MH=3a,QH=2a,由勾股定理求出MQ2,分别求出两正方形的面积公式,继而求出比值.
11.【答案】20
【解析】【解答】解:如图,根据题意得AO= ×8=4,BO= ×6=3,
∵四边形ABCD是菱形,∴AB=BC=CD=DA,AC⊥BD.
∴△AOB是直角三角形.
∴ .
∴此菱形的周长为:5×4=20
故答案为:20.
【分析】根据菱形的对角线互相垂直平分的性质,利用对角线的一半,根据勾股定理求出菱形的边长,再根据菱形的四条边相等求出周长即可.
12.【答案】∠BAD=90°(答案不唯一)
【解析】【解答】解:∵四边形ABCD是菱形,
∴当∠BAD=90°或BD=AC时, 四边形ABCD是正方形.
故答案为:∠BAD=90°(答案不唯一).
【分析】有一个角是直角的菱形是正方形,对角线相等的菱形是正方形,据此解答即可.
13.【答案】AC=BD(答案不唯一)
【解析】【解答】解:添加的条件是AC =BD(答案不唯一),
理由如下:∵AC=BD,四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形,
故答案为:AC = BD(答案不唯一).
【分析】利用矩形的判定方法证明即可。
14.【答案】
【解析】【解答】解:如图,连接、,
点、分别是、的中点,
,
正方形的边长为2,
,
点是边长的动点,
,
,
的最大值为.
故答案为:.
【分析】由点E是BC边长的动点可得,利用正方形的性质求得AC的边长,进而得到AE的取值范围,再通过三角形的中位线定理求得MN的最大值.
15.【答案】
【解析】【解答】解:如图,
∵△ABC是等腰直角三角形,且AC=BC,
∴∠B=∠C=45°,
∵四边形CDHG是矩形,且CD= ,
∴HG=CD= ,∠BGH=90°,
∴∠B=∠BHG=45°,
∴GB=GH=,
∴CG=DH=BC-BG=cm,
∵四边形CDHG是矩形,
∴DH∥BC,
∴∠B=∠DHN=45°,
∵四边形DENM是矩形,且DE=,
∴MN=ED= ,∠NMH=90°,
∴∠MNH=∠MHN=45°,
∴MN=MH=,
∴DM=EN=DN-MH=cm;
同理FQ=PE=,
∵AF=AC-CD-DE-EF=,
∴这样的长方形纸条只能裁出三条,
这三条的总长度为:CG+DM+EN=cm,
∴美术作品的边长为:cm,
∴这个美术作品的面积为:cm2.
故答案为:.
【分析】由等腰直角三角形的性质得∠B=∠C=45°,由矩形的性质得HG=CD= ,∠BGH=90°,从而可推出△BHG是等腰直角三角形,得GB=GH=,CG=DH=BC-BG=cm,同理可求出DM、PE得长,可得到裁剪出的矩形纸条的总长度,进而结合图③找出美术作品的边长,最后根据正方形面积计算方法计算可得答案.
16.【答案】;
【解析】【解答】解:连接BD,交BD于点M,
在△DFM和△BEM中
∴△DFM≌△BEM(AAS),
∴BM=DM,FM=ME,
∵正方形ABCD,
∴∠A=90°,AB=AD=2,
∴,
∴,
设ME=x,则BE=2x,
∴BE2+ME2=BM2即x2+4x2=2,
解之:x=,
∴;
如图,将KL,HJ,HI,HG平移,
设BG=GH=HI=IJ=JK=KL=LD=x,可知DS=2x, SO=1.5x,
∴(1.5x)2+(2x)2=2
解之:x=.
故答案为:,.
【分析】连接BD,交BD于点M,利用AAS证明△DFM≌△BEM,利用全等三角形的性质可证得BM=DM,FM=ME,利用正方形的性质可得到∠A=90°,AB=AD=2,利用勾股定理求出BD的长,可得到BM的长;设ME=x,则BE=2x,利用勾股定理可得到关于x的方程,解方程求出x的值,可得到BE的长;如图,将KL,HJ,HI,HG平移,设BG=GH=HI=IJ=JK=KL=LD=x,则DS=2x, SO=1.5x,利用勾股定理可得到关于x的方程,解方程求出x的值,即可求解.
17.【答案】(1)证明:∵交于点E,交于点F.
∴四边形AEDF是平行四边形,∠EAD=∠ADF,
∵是的一条角平分线,
∴∠EAD=∠FAD,
∴∠ADF=∠FAD,
∴FA=FD,
∴四边形AEDF是菱形;
(2)解:当△ABC是直角三角形,∠BAC=90°,此时∠C=55°,四边形AEDF是正方形,
理由:∵△ABC是直角三角形,∠BAC=90°,
由(1)可得四边形AEDF是菱形,
∴四边形AEDF是正方形,
∵∠B=35°,∠BAC=90°,
∴∠C=55°,
故答案为:55°.
【解析】【分析】(1)先利用角平分线的定义及等量代换可得∠ADF=∠FAD,利用等角对等边的性质可得FA=FD,再结合四边形AEDF是平行四边形,可得四边形AEDF是菱形;
(2)根据△ABC是直角三角形,∠BAC=90°,四边形AEDF是菱形,可得四边形AEDF是正方形,再结合∠B=35°,∠BAC=90°,求出∠C=55°即可.
18.【答案】证明:∵ 四边形ABCD为正方形,
∴ AB=BC=BC=CD,∠ABE=∠BCF=90°,
∵ CE=DF,
∴ BC+CE=CD+DF,即BE=CF,
∴ △ABE≌△BCF(SAS),
∴ AE=BF.
【解析】【分析】根据正方形的性质得AB=BC=BC=CD,∠ABE=∠BCF=90°,推出BE=CF,依据SAS判定△ABE≌△BCF,根据全等三角形的对应边相等即可求得.
19.【答案】(1)解:长方形的周长为
(2)解:正方形的周长为,
∴正方形的边长为,∴正方形的面积为
【解析】【分析】(1)直接根据长方形的周长公式进行求解即可;
(2)根据正方形与长方形的周长相等求得正方形的边长,再利用正方形的面积公式进行计算即可求解.
20.【答案】(1)证明:∵AB∥CD,
∴∠ABF=∠CDE,
∵ BE=EF=FD,
∴BF=DE,
在△ABF和△CDE中
∴ △ABF≌△CDE(AAS)
(2)解:①或②,四边形 AECF 是菱形,
如图,
已知①即 ∠ABD=30° ,
理由:
∵△ABF≌△CDE,
∴AF=CE,∠AFB=∠CED
∴AF∥CE,
∴四边形AECF是平行四边形,
∵∠ABD=30°,∠BAF=90°,BE=EF,
∴AE=BF,AF=BF,
∴AE=AF,
∴四边形AECF是菱形;
【解析】【分析】(1)利用平行线的性质可证得∠ABF=∠CDE,利用已知可得到BF=DE,再利用AAS可证得结论.
(2)已知①即 ∠ABD=30° ,利用全等三角形的性质及平行线的性质可证得AF=CE,AF∥CE,由此可推出四边形AECF是平行四边形;再利用直角三角形斜边上的中线等于斜边的一半和30°角所对的直角边等于斜边的一半去证明AE=AF,据此可证得四边形AECF是菱形.
21.【答案】(1)证明:由折叠得:
∵EG平分∠CEF,
∴
∴
∵
∴
∴.
(2)解:∵四边形ABCD为长方形,
∴
由折叠得:
∴
∵AD∥BC,
∴
∵,
∴.
【解析】【分析】(1)由折叠得∠AEB=∠AEF,然后根据角平分线的定义和平角的定义即可得∠AEG=90°,结合题目已给信息,由同旁内角互补,两直线平行可证HG∥AE;
(2)根据矩形的性质得到∠B=90°,AD∥BC,然后根据折叠的性质和三角形内角和定理即可求出∠BEA的度数,进而由二直线平行,内错角相等得到∠DAE的度数,最后根据二直线平行,同位角相等即可求解.
22.【答案】(1)证明:如图,作,.
,,
四边形是正方形,
,
四边形是矩形,
,
点是正方形对角线上的点,
,
四边形是矩形,
,
,
在和中,
,
≌,
;
(2)解:四边形是矩形,,
矩形是正方形,
,,
四边形是正方形,
,,,
,
≌,
,,
,
,
,,
,
的面积
(3)解:如图,当点在线段上时,
四边形是正方形,
,
,,
;
如图,当点在线段的延长线上时,
,,
,
综上,的度数为或.
【解析】【分析】本题主要考查正方形的基本性质、矩形的判定和性质、三角形全等的判定及性质.
(1)作,,结合题意可证得四边形是矩形,然后运用矩形和正方形的性质可得到≌,进而得到答案;
(2)根据矩形和正方形的性质运用等量代换的方法可证得:≌,得到,进而表示出的面积y的表达式;
(3)分点在线段上和点在线段的延长线上两种情况进行求解即可.
23.【答案】(1)解:∵四边形ABCD是平行四边形,∴AB= CD=3cm, 在Rt△ABE中,∠AEB=90 ,∠B=45°,∴设BE=AE=xcm,则有x2+x2 =(3)2,解得x=3,即AE的长度为3cm.
(2)解:∵点M,N分别以A,C为起点,以1 cm/s的速度沿AD,CB边运动,设点M,N运动的时间为t s(0≤t≤6),
∴AM=CN=t cm.∵AM∥ CN,∴四边形AMCN为平行四边形,
∴当AN=AM时,四边形AMCN为菱形.
∵BE=AE=3 cm,EN=(6-t)cm,∴AN2=32+(6-t)2,
∴32+(6-t)2=t2 ,解得t=
故当t为时,四边形AMCN为菱形.
(3)解:∵MP⊥BC于点P,NQ⊥AD于点Q,QM∥NP,∴四边形MPNQ
为矩形,∴当QM=QN时,四边形MPNQ为正方形.∵AM=CN=tcm,
BE=3 cm,∴AQ=EN=BC -BE -CN=9-3-t=(6-t)cm,
∴QM=|AM-AQ|=|t-(6-t)|=、2t-6|(注:分点Q在点M的左右两种情况).
∵QN=AE=3 cm,∴|2t-6|=3,解得t=4.5 或t=1.5.
故当t为4.5或1.5时,四边形MPNQ为正方形.
【解析】【分析】(1)根据勾股定理,列算式解答即可;
(2)根据菱形的判定方法,邻边相等的平行四边形为菱形,结合勾股定理,可解答;
(3)根据正方形的判定方法,邻边相等的矩形为正方形,再结合勾股定理可解答,但需要分Q在点M的左右两种情况,所以列式时需加上绝对值.
24.【答案】(1)证明:∵四边形OBCA为矩形,
∴OB//CA,BC//OA,
∴∠BOC=∠OCA,
由折叠的性质可得:∠BOC=2∠EOC,∠OCA=2∠OCH,
∴∠EOC=∠OCH,
∴OE//CH,
又∵BC//OA,
∴四边形OECH是平行四边形;
(2)解:四边形OECH是菱形.理由如下:
由折叠的性质可得∠EFO=∠EBO=90°,∠CFH=∠CAF=90°,
∵点F,G重合,
∴EH⊥OC,
又∵四边形OECH是平行四边形,
∴平行四边形OECH是菱形,
∴EO=EC,
∴∠EOC=∠ECO,
又∵∠EOC=∠BOE,
∴∠EOB=∠EOC=∠ECO=30°,
点A的坐标是(5,0),
∴OA=5,
由直角三角形的性质可得:OB=
∴点B的坐标是(0,);
(3)解:当点F在点O,G之间时,如图3,
由折叠性质得:OF=OB,CG=CA,
而OB=CA,
∴OF=CG,
∵点F,G将对角线OC三等分,
∴AC=OF=FG=GC,
设AC=m,则OC=3m,
在Rt△OAC中,OA=5,
由勾股定理得:AC2+OA2=OC2,
即:m2+52=(3m)2,解得m=,
∴OB=AC=,
∴点B的坐标是(0,);
当点G在O,F之间时,如图4,
同理可得OF=CG=AC,
设OG=n,则AC=GC=2n,
在Rt△OAC中,OA=5,
由勾股定理得:AC2+OA2=OC2,
即:(2n)2+52=(3n)2,解得n=,
∴AC=OB=2,
∴点B的坐标是(0,2).
故B的坐标是(0,)或(0,2).
【解析】【分析】(1)根据矩形的性质得OB∥CA,BC∥OA,再利用平行线的性质得∠BOC=∠OCA,然后根据折叠的性质得到∠BOC=2∠EOC,∠OCA=2∠OCH,所以∠EOC=∠OCH,根据平行线的判定定理得OE∥CH,根据平行四边形的判定方法:两组对边分别平行的四边形是平行四边形,即可得证;
(2)先根据折叠的性质得∠EFO=∠EBO=90°,∠CFH=∠CAF=90°,由点F,G重合得到EH⊥OC,根据菱形的判定方法:对角线垂直的平行四边形是菱形,得到四边形OECH是菱形,则EO=EC,所以∠EOC=∠ECO,而∠EOC=∠BOE,根据三角形内角和定理可计算出∠EOB=∠EOC=∠ECO=30°,在Rt△OBC中,根据含30度的直角三角形三边的关系得OB=,于是得到点B的坐标是(0,);
(3)分类讨论:当点F在点O,G之间时,如图3,根据折叠的性质得OF=OB,CG=CA,则OF=CG,所以AC=OF=FG=GC,设AC=m,则OC=3m,在Rt△OAC中,根据勾股定理得m2+52=(3m)2,解得m=,则点B的坐标是(0,);当点G在O,F之间时,如图4,同理可得OF=CG=AC,设OG=n,则AC=GC=2n,在Rt△OAC中,根据勾股定理得(2n)2+52=(3n)2,解得n=,则AC=OB=2,所以点B的坐标是(0,2),即可得解.
1 / 1
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
