7.1~7.3复习

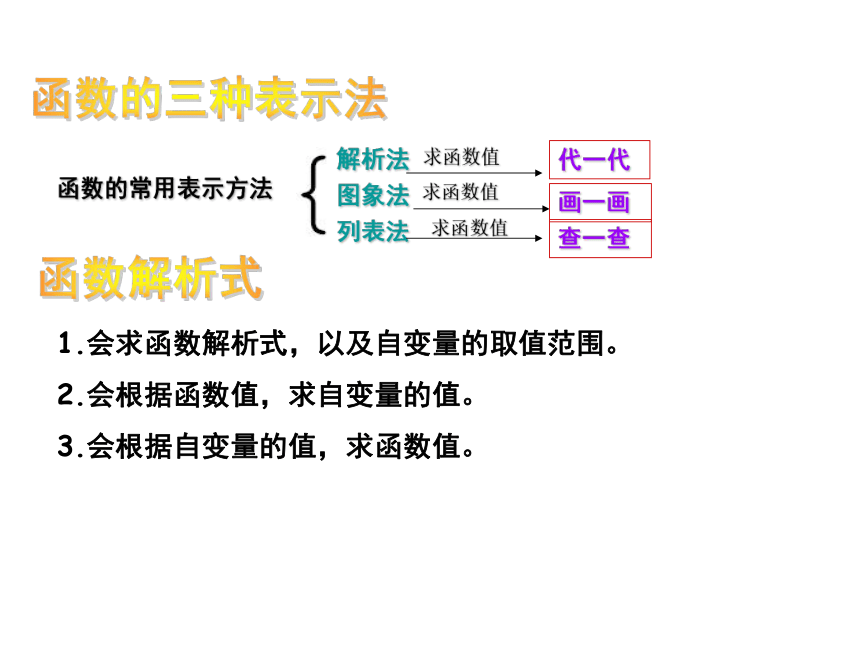
课件13张PPT。7.1-7.3复习在同一个过程中,固定不变的量称为常量.在同一个过程中,可以取不同数值的量称为变量.常量与变量函数的概念 一般地，在某个变化过程中，设有两个变量x,y，如果对于x的每一个确定的值，y都有唯一确定的值，那么说 y是x的函数，x叫做自变量。练习1：下列y与x的关系式中，y是x的函数是（ ）可取若干个特殊值判断。D函数的三种表示法画一画代一代查一查函数解析式1.会求函数解析式，以及自变量的取值范围。
2.会根据函数值，求自变量的值。
3.会根据自变量的值，求函数值。练习2：小刚、爸爸、爷爷同时从家中出发到达同一目的地后都立即返回。小刚去时骑自行车，返回时步行；爷爷去时步行，返回时骑自行车；爸爸往返都步行。三个人步行的速度不等，小刚与爷爷骑车的速度相等，每个人的行走路程与时间的关系分别是所给三个图像中的一个。（1）从家里到目的地共有多少米？
（2）走完一个往返，小刚、爸爸、爷爷各用了多少时间？
（3）小刚与爷爷骑车的速度是多少？
（4）小刚、爸爸、爷爷步行的速度各是多少？解：1）从家到目的地共1200m
2）走完一个往返，小刚用了21分，爸爸用了24分，爷爷用了26分
3）小刚和爷爷骑车速度：1200÷6=200米/分
4）爷爷：1200÷20=60米/分，爸爸：1200÷12=100米/分
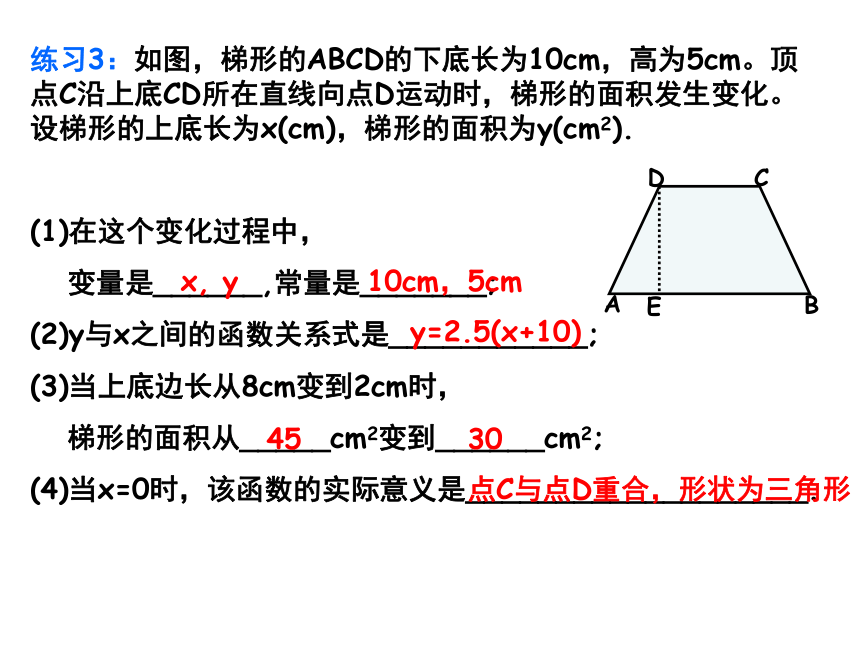
小刚：1200÷15=80米/分小刚爷爷爸爸练习3：如图，梯形的ABCD的下底长为10cm，高为5cm。顶点C沿上底CD所在直线向点D运动时，梯形的面积发生变化。设梯形的上底长为x(cm)，梯形的面积为y(cm2).
(1)在这个变化过程中，
变量是______,常量是_______;
(2)y与x之间的函数关系式是___________;
(3)当上底边长从8cm变到2cm时，
梯形的面积从_____cm2变到______cm2;
(4)当x=0时，该函数的实际意义是___________________.
x, y10cm，5cmy=2.5(x+10)4530点C与点D重合，形状为三角形ABCDE练习4：等腰三角形的周长为20，腰长为x，底边长为y。
（1）写出y关于x的函数解析式。
（2）求自变量x的取值范围；
（3）当底边长尾腰长的一半时，求腰长；
（4）若三角形是等边三角形，求此时x的值。解：（1）y=20-2x
（2）∵x＞0，y＞0，2x＞y 解得：5＜x＜10（3）当y=?x时，
?x=20-2x
∴ x=8，
∴ 即腰长为8 （4）∵三角形是等边三角形
∴当y=x时，
x=20-2x
∴ x=20/3
自变量的取值要从两个变量的实际意义考虑：x和y两方面兼顾！练习5：某辆摩托车油箱中能装汽油30升，摩托车每行驶20km耗油1升。
（1）写出余油量y(升)与行驶x(千米)之间的函数关系式。
（2）求自变量x的取值范围；
（3）当行驶400千米时，油箱中还有油多少升？
（4）如果加满油开出并且需要回来，最多能行驶多远？解：（1）（2）∵x≥0，y≥0解得：0≤x≤600（3）当x=400时，y=30-20=10
∴油箱中还有油10升。（4）当y=0时，∴x=600
∴加满油开出并且回来，最多行驶300米远。自变量的取值要从两个变量的实际意义考虑：x和y两方面兼顾！练习6 求下列函数，自变量的取值范围:x可取任何实数一次函数正比例函数一次函数y=kx（k为常数，且k≠0） y=kx+b（k、b为常数，且k≠0）当b=0时，一次函数y=kx+b就变形为正比例函数y=kx1、若y =(m-2)x m2-3 - 4是一次函数, 则m = ____ -2 解： 解：（1） 解：（2）2、已知函数y=(m+1)x+(m2-1),
1)当m取什么值时， y是x的一次函数？
2)当m取什么值时，y是x的正比例函数？练习7练习8已知y1是关于x正比例函数，y2是关于x的一次函数，
且当x=1时，y1+y2=6；当x=-1时，y1-y2=-10；
当x=2时，y1=6y2，求这两个函数的解析式。练习9某市自来水公司为限制单位用水，每月只给某单位计划内用水
2500m3，计划内用水每立方米收费0.9元，超计划部分每立方
米按1.5元收费。
1）写出该单位水费y(元)与每月用水量x(m3)之间的函数关系式。
2）某月该单位用水2000m3，应付水费多少元？
若用水3000m3，应付水费多少元？
3）若某月该单位付水费3300元，则该单位用水多少？练习10直线y=kx+b经过点A(-2,0)和y轴正半轴上的一点B，若△ABO
（O为坐标原点）的面积为2，求函数的解析式？O解：设点B坐标为(0, YB)
S△ABO =?×2×yB=2
∴ yB=2
∴B的坐标为(0, 2)
当x=-2时，y=0；当x=0时，y=2解得：函数的解析式为：y=x+2