7.4.1习题分析

课件15张PPT。学法P88，7.4.1一次函数的图像点(x0,y0)在函数y=kx+b图像上，是指：
(x0,y0)代入后满足y0=kx0+b1.下面哪个点不在函数y=-2x+3的图像上( )
A.(-5,13) B.(0.5,2) C.(3,0) D.(1,1)当x=3时，y=-2×3+3=-3≠0
∴(3,0)不在函数图像上。C平移规律：直线y=kx+b是由y=kx向上平移b个单位而来。2.将直线y=2x+1向下平移3个单位，得到的直线解析式应为_______y=2x+1-3=2x-2y=2x-2y=kx+b与坐标轴交点：
与x轴交点：把y=0代入求x，形式(x0,0)
与y轴交点：把x=0代入求y，得到点(0,b)3.一次函数y=-2x+6的图像与x轴交点的坐标是_____，
与y轴交点坐标为_____，图像与坐标轴围成的三角形面积是
_______(3,0)(0,6)9通过画图，判断所经过的象限。4.直线y=4x经过第____象限，直线y=4x-5经过第______象限。当x=0，y=0
当x=1，y=4
y=4x过(0,0),(1,4)一,三y=4x-5
过(0,-5),(1,-1)一,三,四5.直线y=2x+b与直线y=-?x-3交于y轴上一点，则b=___y=-?x-3过点(0,-3)
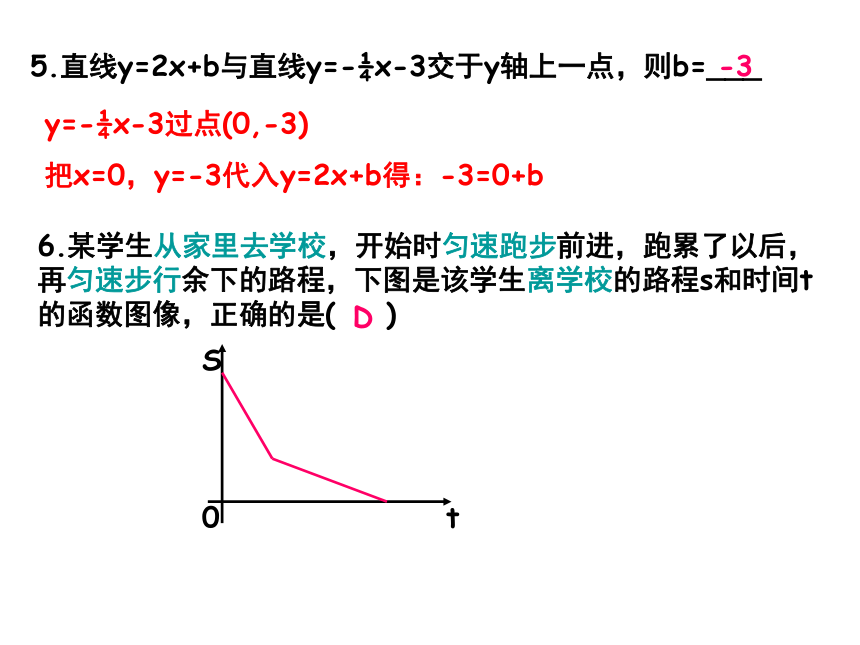
把x=0，y=-3代入y=2x+b得：-3=0+b-36.某学生从家里去学校，开始时匀速跑步前进，跑累了以后，再匀速步行余下的路程，下图是该学生离学校的路程s和时间t的函数图像，正确的是( )D7.已知一次函数y=kx+b的图像经过点(0,-1)和点(1,-2).
(1)求函数解析式；
(2)在直角坐标系中画出它的图像；
(3)试判断(-a,3a+1)是否在函数图像上？解：(1) y=kx+b
x=0，y=-1；x=1，y=-2；
∴解析式为y=-x-1
(2)由题意：图像过(0,-1),(1,-2)(3)当x=-a时，y=-(-a)-1=a-1≠3a+1
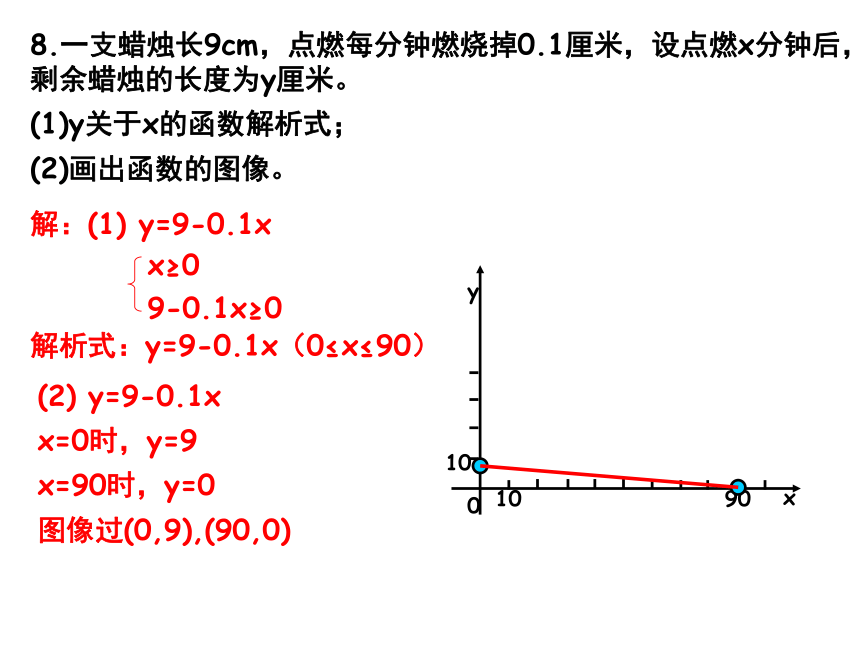
∴点(-a,3a+1)不在函数图像上。8.一支蜡烛长9cm，点燃每分钟燃烧掉0.1厘米，设点燃x分钟后，剩余蜡烛的长度为y厘米。
(1)y关于x的函数解析式；
(2)画出函数的图像。解：(1) y=9-0.1x解析式：y=9-0.1x（0≤x≤90）(2) y=9-0.1x
x=0时，y=9
x=90时，y=0
图像过(0,9),(90,0)9.若y是x的一次函数，图像过点(-3,2)，且与直线y=4x+6交于
x轴上同一点；
(1)求此一次函数的解析式；
(2)在(1)的一次函数图像上求出到y轴的距离等于1的点的坐标。解：(1) 当y=0时，4x+6=0
∴x=-1.5，即函数与x轴交点(-1.5,0)
设y=kx+b（k≠0）
x=-3，y=2；x=-1.5，y=0∴解析式为y=-4/3x-2
(2)由题意：图像过(-3,2),(-1.5,0)x=-1时，y=-2/3
x= 1时，y=-10/3
所求点为(-1,-2/3)
( 1,-10/3)课时P121，7.4.1一次函数的图像1.一次函数y=kx+b(k≠0)的图像是_______，正比例函数y=kx
(k≠0)的是经过______的一条直线。一条直线原点2.已知一次函数y=kx+5的图像经过点(-1，2)，则k=______33.已知点A的坐标为(-1，-2)，点B的坐标为(1,-1)，点C坐标为(5,1)，其中在直线y=-x+6上的点是______，在直线y=3x-4上的点为______.点C点B4.函数y=3x-6的图像是( )
A.过点(0,-6)，(0,-2)的直线
B.过点(0,2)，(1,-3)的直线
C.过点(2,0)，(1,3)的直线
D.过点(2,0)，(0,-6)的直线Dy=kx+b：k＞0：图像过一,三象限，y随x的增大而增大
k＜0：图像过二,四象限，y随x的增大而减小5.下列一次函数中，y随x的增大而减小的是( )
A.y=3x B.y=3x-2 C.y=3+2x D.y=-3x-2D6.(1)在同一直角坐标系中，作出下面一次函数y=-2x，y=-2x+1，
y=-2x-1的图像；
(2)由(1)画图，你觉得三条直线有何位置关系？
(3)直线y=-2x-1可由直线y=-2x怎样平移得到？解：(1) y=-2x
x=0时，y=0；x=1时，y=-2
图像过(0,0),(1,-2)
同理：y=-2x+1过(0,1),(1,-1)
y=-2x-1过(0,-1),(1,-3)解：(2)平行关系。
(3)直线y=-2x-1可由直线y=-2x向下平移一个单位而得。7.已知函数y=(2m-1)x-2+m
(1)若函数图像经过原点，求m的值；
(2)若这个函数是一次函数，且y随x增大而减小，求m的取值范围。解：(1)由题意：当x=0时，y=0，则：
-2+m=0，m=2
(2)∵y随x增大而减小
∴2m-1＜0
m＜?B组8.已知一次函数y=kx-k+4的图像与y轴的交点坐标是(0，-2)，那么这个一次函数的表达式是______y=6x-29. 10.AD11.一农民带了若干千克自产的土豆进城出售，为了方便，他带了一些零钱用，按市场价售出一些后，又降价出售，售出土豆千克数与他手中持有钱数(含备用零钱)的关系如图所示，结合图像回答下列问题：
(1)农民自带的零钱是多少？
(2)降价前他每千克土豆出售的价格是多少？
(3)降价后他按每千克0.4元将剩余土豆售完，
这时他手中的钱(含备用零钱)是26元，
问他一共带了多少kg土豆？解：(1)农民自带的零钱是5元。
(2)降价前他每千克土豆出售的价格:
(20-5)÷30=0.5元
(3)他一共带了土豆：(26-20)÷0.4+30=45kg课外练习A组1.C2.如果函数y=ax+b(a＜0,b＜0)和y=kx(k＞0)的图像交于点P，那么点P应该位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限C3. y=-2x-2(平行：k相同) 4. (2/3,0)，(0,3)，9/45. y=-2x+26.已知一次函数图像经过点(1,1)和(-1,-5).
(1)求该一次函数的表达式；
(2)求此一次函数图像与两坐标轴围成的三角形的面积；
(3)另一条直线与该一次函数图像交于点A(-1,m)，且与y轴交点的纵坐标为4，求这条直线的解析式。解：(1)设y=kx+b（k≠0）
x=1，y=1；x=-1，y=-5∴解析式为y=3x-2
(2) y=3x-2与两坐标轴交于：
(2/3,0)，(0,-2)
∴S△ABC=?×2/3×2=2/3(3)点A(-1,m)在y=3x-2上
∴m=3×(-1)-2=-5
点A(-1,-5)
∴另一直线经过(-1,-5),(0,4)
解法同(1)可得：
解析式为：y=9x+47.一次函数y1=kx+b与y2=x+a的图像如图，则下列结论
①k＜0； ②a＞0； ③当x＜3时，y1＜y2中，
正确的个数是( )
A.0个 B.1个 C.2个 D.3个解：当x＜3时，y1＞y2
当x＞3时，y1＜y2B8.为调动销售人员的积极性，A,B两公司采取如下工资支付方式：A公司每月2000元基本工资，另加销售额的2%作为奖金；B公司每月1600元基本工资，另加销售额的4%作为奖金。已知A、B公司两位销售员小李、小张1~6月份的销售额如下表：
（1）请问小李与小张三月份工资各是多少？
解：(1)小李：2000+14000×2%=2280元；
小张：1600+11000×4%=2040元。（2）小李1~6月份的销售额y1与月份x的函数解析式是y1=1200x+10400，
小张1~6月份的销售额y2也是月份x的一次函数，请求出y2与x的函数解析式？解：(1)设y2=kx+b（k≠0）
x=1，y2=7400；x=2，y2=9200∴解析式为y2=1800x+5600（3）如果7~12月份两人的销售额也分别满足（2）中两个一次函数的关系，问几月份起小张的工资高于小李的工资。解：1600+4%(1800x+5600)＞2000+2%(1200x+10400)
∴x＞8
答：从9月份起小张的工资高于小李的工资。9.某空中加油飞机接到命令，立即给另一架正在飞行的战斗机进行空中加油。在加油过程中，设战斗机进行空中加油。在加油过程中，设战斗机的油箱余油量为Q1，加油飞机的加油油箱余油量为Q2，加油时间为t分钟，Q1、Q2与t之间的函数关系图像如图所示，结合图像回答问题：
(1)加油飞机的加油油箱中装载了多少油？
将这些油全部加给战斗机需多长时间？解：(1)加油飞机的加油油箱中，装载了30t油，将这些油全部加给战斗机需10min(2)求加油过程中，战斗机的余油量Q1(t)与时间 t(min)的函数关系式；(2)设Q1=kt+40
将(10,69)代入得：k=2.9
∴Q1=2.9t+40（t≥0）(3)战斗机加完油后，以原速度继续飞行，需10h到达目的地，油料是否够用？请说明理由。(3)40+30-69=1(t), 即战斗机10min用了1t油；
10h=600min需用油60t，而69＞60
∴油料够用