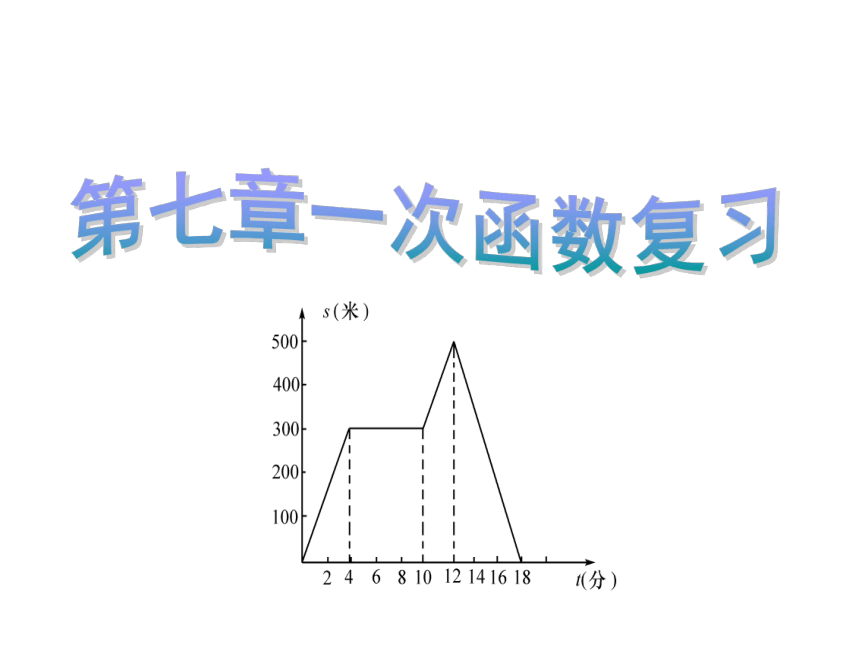
第七章 一次函数复习

课件17张PPT。第七章一次函数复习轻松过关请观察加油机为汽车加油过程中，
哪些量在改变，哪些量不变？在一个过程中,固定不变的量称为常量
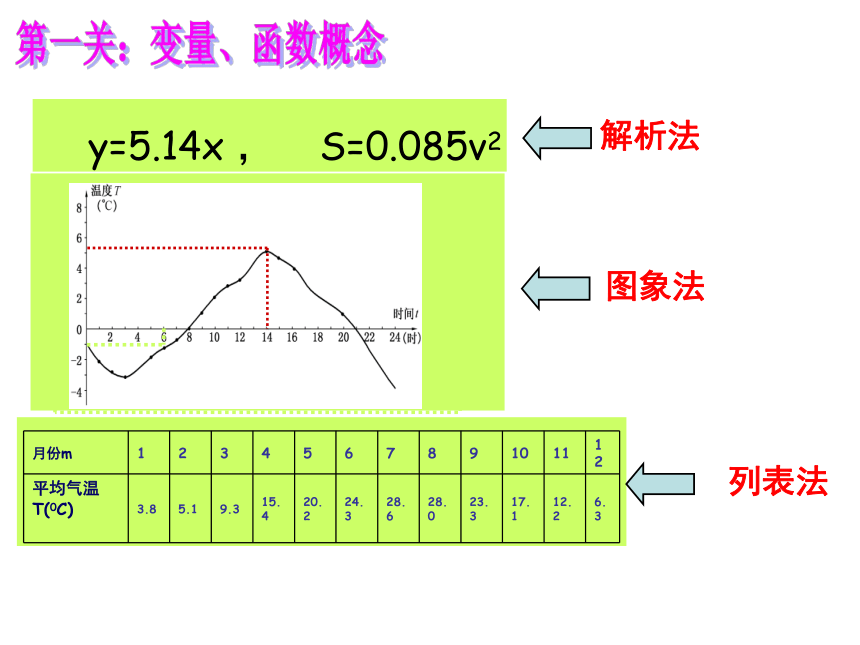
在一个过程中,可以取不同数值的量称为变量第一关：变量、函数概念第一关：变量、函数概念下列函数中，哪些是一次函数？哪些是正比例函数？第二关：一次函数概念是一次函数
不是正比例函数不是一次函数,不是正比例函数是一次函数
不是正比例函数是一次函数
是正比例函数不是一次函数
不是正比例函数（1）等号两边的代数式都是整式；
（2）自变量的次数是一次；1、已知y关于x的函数y=(a-1)x+a+1,
当a满足 时，它为一次函数；
当a满足 时，它为正比例函数。定义:函数y=kx ＋b (k、b为常数，k ≠０)叫做一次函数。
当b =０ 时，函数y=kx(k ≠０)叫做正比例函数。2、点P（2，-3）在函数y=kx+1的图象上，k= 。-2点在函数图象上，则点的坐标一定满足函数解析式。第二关：一次函数概念正比例函数y=kx（k≠0)的性质：
　　⑴当k>0时，图象过______象限；y随x的增大而______
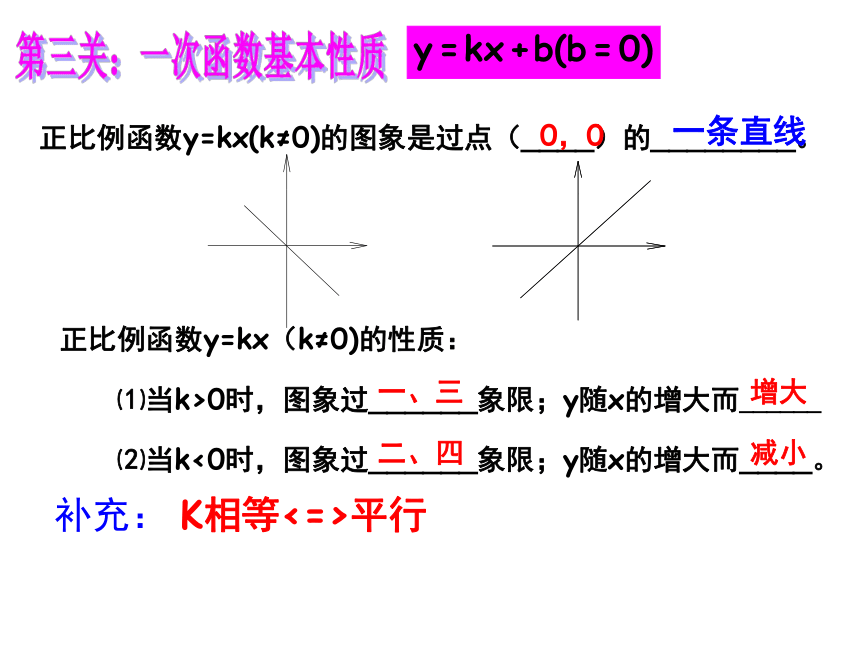
　　⑵当k<0时，图象过______象限；y随x的增大而____。一、三增大二、四减小正比例函数y=kx(k≠0)的图象是过点（____）的________。
0，0 一条直线第三关：一次函数基本性质补充： K相等<=>平行 k < 0一、二、三一、三、四一、二、四二、三、四 k > 0 k < 0 b < 0 b < 0 b > 0 b > 0 k > 0 k > 0 k < 0 k < 0 b < 0 b < 0 b > 0 b > 0第三关：一次函数基本性质 k > 01、一次函数y=-3x+2图像过_________ 象限，
y值随x的增大而______减小2、已知一次函数的图像过点（ 0 ，-1），且y随x的
增大而增大，这个一次函数的解析式可能是______
（只需写一个满足条件的解析式即可）3、已知函数y=kx+b与函数y=2x+2平行，且过点
（0，1），这个一次函数的解析式可能是______第三关：一次函数基本性质y=2x+1一、二、四利用一次函数的图象，求下列二元一次方程组的解（或近似解）??x+y=2??y= 2x-1●第四关：一次函数基本应用已知一次函数的图象经过点A（1，1），B（-2，7），
求这个一次函数的解析式。第四关：一次函数基本应用变一变：已知y-6与x+2成正比例，且当x＝3时，y＝－4；
求y关于x的函数解析式。整体思想的运用y-6=-2(x+2)已知y-6与x+2成正比例，且当x＝3时，y＝-4；
求y关于x的函数解析式。第五关：一次函数(变式练习)解：设y关于x的函数解析式为y-6=k(x+2)得：解这个方程，得k=-2∴ y关于x的函数解析式为(k≠0)-4-6=k(3+2) y=-2x y=-2x+2msO2462846ABL如图,线段AL表示弹簧的长度s(cm)与所挂物体的质量m(kg)之间的关系的图象,请结合图象回答下列问题:(1):问题中的两个变量s与m之间是不是一次函数关系?(3):s与m之间的函数关系是_______________ _ ;(4):当所挂物体的质量为3kg时,弹簧的长度 s=___cm; (kg)(cm)是s=0.5m+67.5归纳:运用一次函数模型解决实际问题的基本步骤是：6根据图象判断函数的类型用待定系数法求出函数解析式解决有关函数的实际问题(0≤m≤6)第五关：一次函数(变式练习)(2):由图知弹簧的原长____cm.你过关了吗?函数图象与生活实际的联系你会看图吗？如图反映的过程是：周末早上8：00张占一从家跑步到体育馆，锻炼一阵后，散步走回家，其中t表示时间，S表示离家的距离。（1）求张占一从家跑步到体育馆这段函数图象的解析式；（2）求出张占一散步回家这段函数图象的解析式；（3）回答张占一在体育馆用去的时间是多少分钟？张占一在OA和BC两段时间内的速度什么时候比较大？S（m）02250153080t（min）ABCO（4）求张占一离家1800m时的时间是几时几分?分类讨论的思想1800合作学习二、在具体的实际情景中,用一次函数解决问题三、用整体思想解决 数学问题实际问题 求函数解析式 计算问题 本节课我们复习了哪些数学知识和数学思想方法?一、用待定系数法求函数解析式今天我们学会了…四、求函数交点的方法：计算和看图