第五章 一元一次不等式复习

课件19张PPT。一元一次不等式复习课一. 知识体系1、 不等式的性质
<1> 若a>b, 则a+c>b+c
<2>若a>b, c>0 则ac>bc
若c<0, 则ac<3>若a>b, c>d 则a+c>b+d
同向不等式可以相加但不能相减
（ x－5y）2≥0写一写
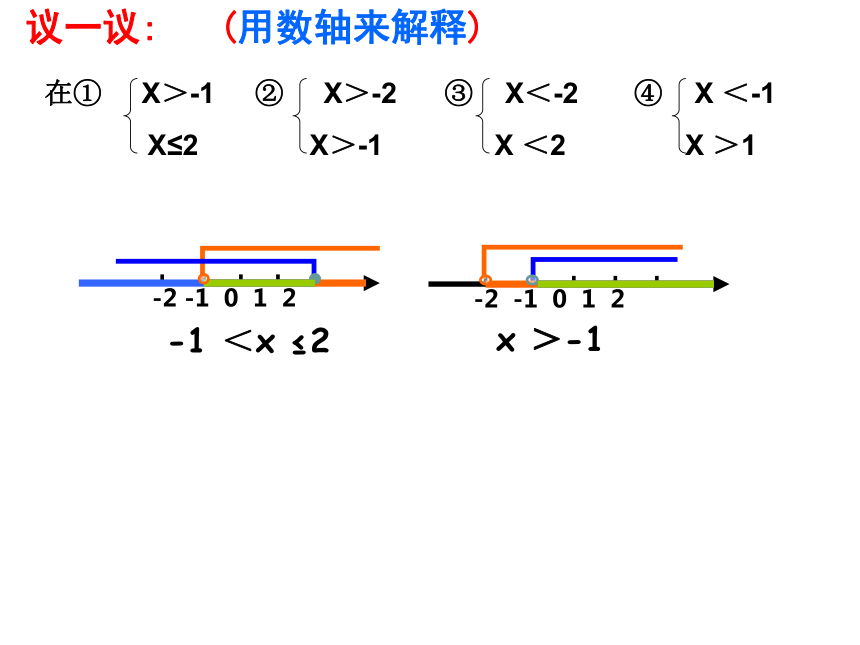
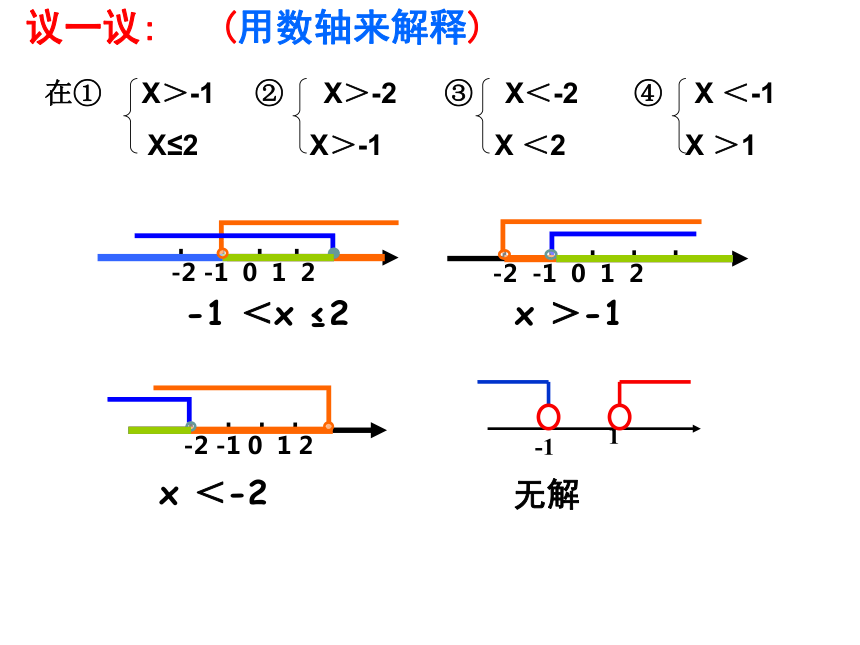
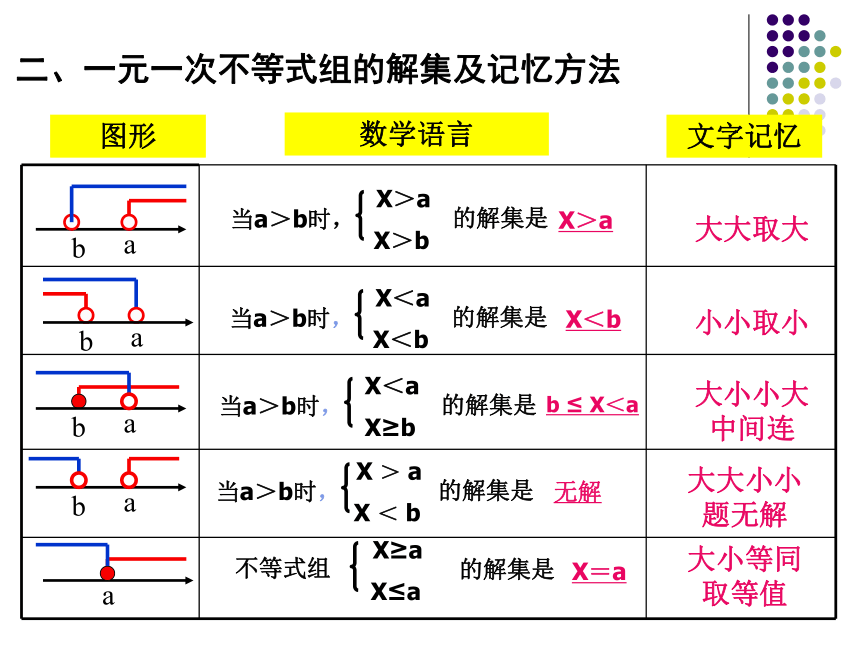
用不等式表示下列数量关系：(1)2x与1的和小于零.(2)x的一半与3的差不大于2.(3)a是负数.(4)a与b的和是非负数.2x+1<0x-3≤2a<0a+b ≥ 0(5)X的 与y的5倍的差的平方是一个非负数.议一议: (用数轴来解释)-1＜x≤2议一议: (用数轴来解释)x ＞-1-1 ＜x ≤2 议一议: (用数轴来解释)x ＜-2-1 ＜x ≤2x ＞-1无解大大取大X＞a小小取小X＜b大小小大中间连b ≤ X＜a大小等同取等值X＝a大大小小题无解无解文字记忆数学语言图形二、一元一次不等式组的解集及记忆方法4、由不等式（m-5）x＞m-5变形为x＜ 1，
则m需满足的条件是___________2、若a ＞b，且a、b 、 c为有理数，则ac2___bc2 5、若y=-x+7，且2≤y≤7，则x的取值范围是_____ 3、已知不等式 3(x+1) ≥5x-3 正整数解是_____二、热身训练：1,2,3≥m<50≤x≤51、若a>b,则a-2___b-2,3a___3b,2-a___2-b>><慧眼识金小明和小刚在比较5a与4a的大小关系
时发生了争执.
小明说:5a>4a,例如当a=2时,5a=10,
4a=8,10>8!
小刚说:5a<4a,例如当a=-3时,5a=-15,
4a=-12,-15<-12!
到底小明和小刚谁的判断是正确的呢?
谈谈你自己的看法.如果 m＜n＜0，那么下列结论中错误的是（ ）
A.m-9-n; C. D.思维拓展：C例1：已知不等式3x-a≤0的正整数解是1，2，3，求a的范围
变式1:
不等式3x-a<0的正整数解为1，2，3，求a的范围
变式2:
不等式3x-a>0的负整数解为-1，-2，求a的范围
变式3:
不等式3x-a≥0的负整数解为-1，-2，求a的范围一元一次不等式与一次函数一次函数的图像与一元一次不等式的关系： 一次函数y=kx+b(k≠0)的图像是直线，当kx+b>0，表示图像在x轴上方的部分；当kx+b=0时，表示直线与x轴的交点，当kx+b<0时，表示图像在x轴下方的部分。事实上，既可以运用函数图像解不等式和方程，也可以运用解不等式帮助研究函数问题，函数与不等式及方程三者之间互相渗透，相互作用。一元一次不等式与一次函数1．试一试：作出函数y=2x-4的图象，观察图象回答下列问题： （1）x取何值时，2x-4>0？
（2）x取何值时，2x-4<0？
（3）x取何值时，2x-4>2？一元一次不等式与一次函数Y=2x-4解：根据图像可知： （1）x>2时，2x-4>0 ；（2）x<2时，2x-4<0 ；（3）x<3时，2x-4<2 。 某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg， （1）设生产X件A种产品，写出X应满足的不等式组。 （2）有哪几种符合的生产方案？ （3）若生产一件A产品可获利700元，生产一件B产品可获利1200元，那么采用哪种生产方案可使生产A、B两种产品的总获利最大？最大利润是多少？
一元一次不等式与一次函数1、若|3a-5|=5-3a,则a______.不等式与绝对值，函数等知识结合的应用2、已知一次函数y=(3k-6)x+1,y随x的增大而增大，则k的取值范围是______.3、点P(-2a+1, 5)在第二象限，则a_____.如果关于x的方程3x+a＝x+4的解是非负数，求a的取值范围。 X是非负数不等式与方程结合的应用不等式在生活中的应用仔细阅读对话，根据对话内容，求出饼干和牛奶的标价。
小明：阿姨，我买一盒饼干和一袋牛奶。(递上10元钱)
售货员：小朋友，本来你用10元只能买一盒饼干，要再买一袋牛奶就不够了！不过今天是儿童节，饼干打9折，所以你买两样东西还找你8角钱。
（注意：一盒饼干的标价可是整数哦）