4.6 相似多边形 教学设计2023-2024学年浙教版九年级数学上册
文档属性
| 名称 | 4.6 相似多边形 教学设计2023-2024学年浙教版九年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 506.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-26 00:00:00 | ||
图片预览

文档简介
教学设计
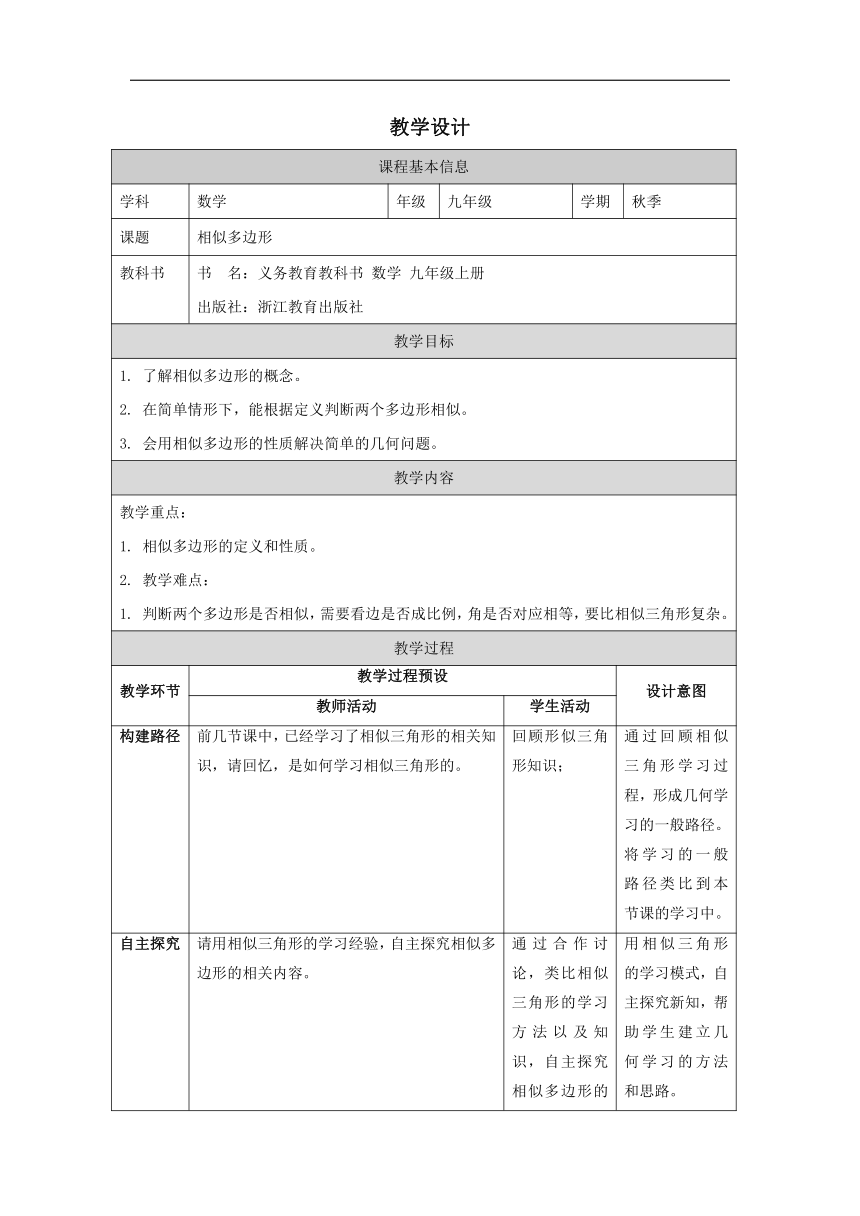
课程基本信息
学科 数学 年级 九年级 学期 秋季
课题 相似多边形
教科书 书 名:义务教育教科书 数学 九年级上册 出版社:浙江教育出版社
教学目标
1. 了解相似多边形的概念。 2. 在简单情形下,能根据定义判断两个多边形相似。 3. 会用相似多边形的性质解决简单的几何问题。
教学内容
教学重点: 相似多边形的定义和性质。 教学难点: 判断两个多边形是否相似,需要看边是否成比例,角是否对应相等,要比相似三角形复杂。
教学过程
教学环节 教学过程预设 设计意图
教师活动 学生活动
构建路径 前几节课中,已经学习了相似三角形的相关知识,请回忆,是如何学习相似三角形的。 回顾形似三角形知识; 通过回顾相似三角形学习过程,形成几何学习的一般路径。将学习的一般路径类比到本节课的学习中。
自主探究 请用相似三角形的学习经验,自主探究相似多边形的相关内容。 通过合作讨论,类比相似三角形的学习方法以及知识,自主探究相似多边形的定义与性质。 用相似三角形的学习模式,自主探究新知,帮助学生建立几何学习的方法和思路。
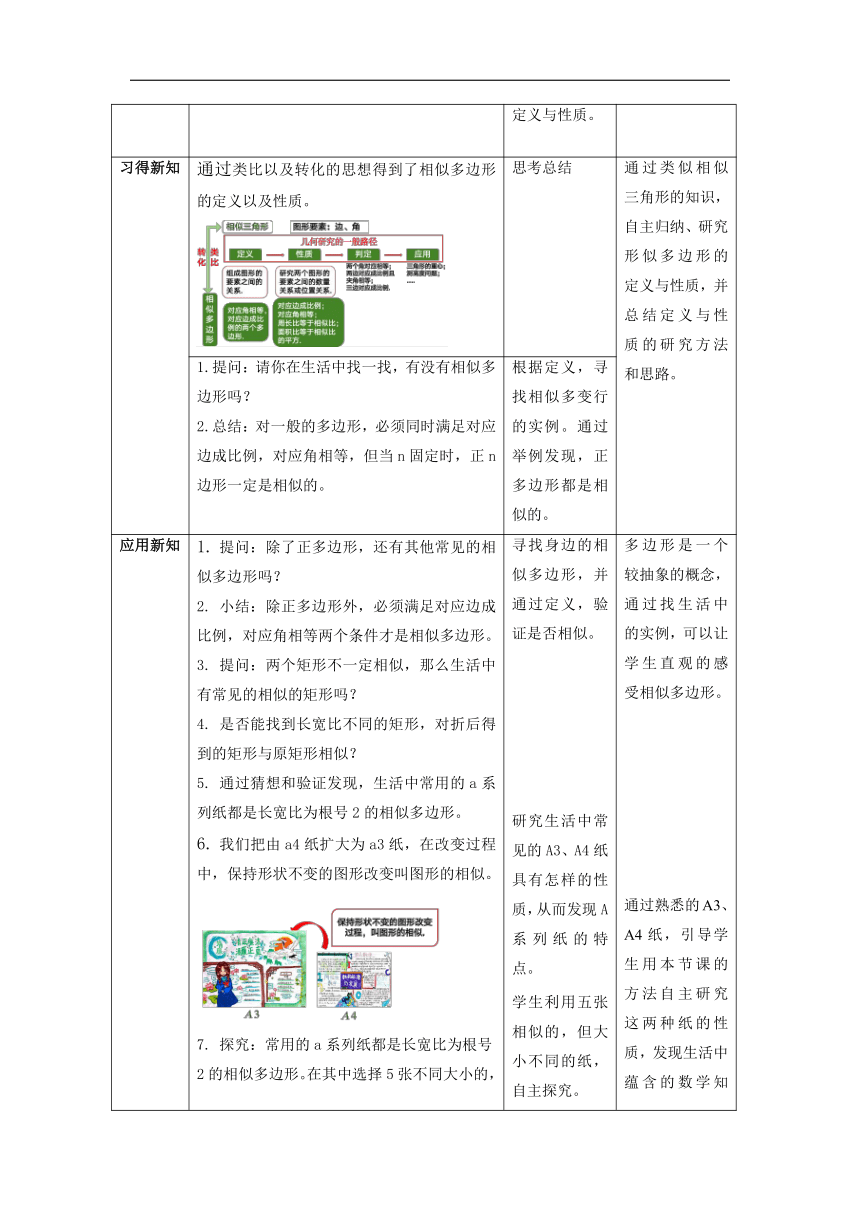
习得新知 通过类比以及转化的思想得到了相似多边形的定义以及性质。 思考总结 通过类似相似三角形的知识,自主归纳、研究形似多边形的定义与性质,并总结定义与性质的研究方法和思路。
1.提问:请你在生活中找一找,有没有相似多边形吗? 2.总结:对一般的多边形,必须同时满足对应边成比例,对应角相等,但当n固定时,正n边形一定是相似的。 根据定义,寻找相似多变行的实例。通过举例发现,正多边形都是相似的。
应用新知 提问:除了正多边形,还有其他常见的相似多边形吗? 小结:除正多边形外,必须满足对应边成比例,对应角相等两个条件才是相似多边形。 提问:两个矩形不一定相似,那么生活中有常见的相似的矩形吗? 是否能找到长宽比不同的矩形,对折后得到的矩形与原矩形相似? 通过猜想和验证发现,生活中常用的a系列纸都是长宽比为根号2的相似多边形。 我们把由a4纸扩大为a3纸,在改变过程中,保持形状不变的图形改变叫图形的相似。 探究:常用的a系列纸都是长宽比为根号2的相似多边形。在其中选择5张不同大小的,你发现什么有趣的现象?你能给出数学解释吗? 寻找身边的相似多边形,并通过定义,验证是否相似。 研究生活中常见的A3、A4纸具有怎样的性质,从而发现A系列纸的特点。 学生利用五张相似的,但大小不同的纸,自主探究。 通过不同摆放方式,发现长宽比为的矩形相关的结论。 多边形是一个较抽象的概念,通过找生活中的实例,可以让学生直观的感受相似多边形。 通过熟悉的A3、A4纸,引导学生用本节课的方法自主研究这两种纸的性质,发现生活中蕴含的数学知识。
8.数学文化:18世纪,时任哥廷根大学教授的德国学者利希滕贝格发现,一张长宽比为根号2的矩形纸,沿着长边对折,不论折叠几次,折叠后的矩形长宽比都保持不变,得到的矩形也都是相似的。我们把这个比例称为利希滕贝格比例或白银比例。 实际生活中用这个比值设计的纸张能避免生产过程中的浪费。同时,也可以确保将a4纸的图案放大到同系列的纸时图案不会变形。 自主探究:国旗尺寸是由国家标准规定了6个型号.请课后通过查阅资料,研究不同型号的国旗之间是否存在一定的比例关系. 感受数学文化,体会生活中处处有数学。 通过数学文化的渗透,感受生活中处处有数学,而数学最终运用于生活中。 同时,通过课后的探究活动,再次巩固研究图形的一般方法和思路。
总结梳理 回顾整节课,是怎么研究相似多边形的? 思考、小结 类比是几何学习的重要方法。从特殊到一般也是重要的数学思维。 通过小结归纳,帮助学生掌握研究几何图形的一般方法和思路。
当堂检测 1.在如图所示的相似四边形中,求边长x和角度α的大小. 如图,矩形ABCD~矩形BCFE,且AD=AE,求AB:AD. 3.把一个长方形划分成三个全等的长方形(如图).若要使每一个小长方形与原长方形相似,则原长方形应满足什么条件 完成、校对、订正 引导学生自主检测本节课掌握情况.
备注:教学设计应至少含教学目标、教学内容、教学过程等三个部分,如有其它内容,可自行补充增加。
课程基本信息
学科 数学 年级 九年级 学期 秋季
课题 相似多边形
教科书 书 名:义务教育教科书 数学 九年级上册 出版社:浙江教育出版社
教学目标
1. 了解相似多边形的概念。 2. 在简单情形下,能根据定义判断两个多边形相似。 3. 会用相似多边形的性质解决简单的几何问题。
教学内容
教学重点: 相似多边形的定义和性质。 教学难点: 判断两个多边形是否相似,需要看边是否成比例,角是否对应相等,要比相似三角形复杂。
教学过程
教学环节 教学过程预设 设计意图
教师活动 学生活动
构建路径 前几节课中,已经学习了相似三角形的相关知识,请回忆,是如何学习相似三角形的。 回顾形似三角形知识; 通过回顾相似三角形学习过程,形成几何学习的一般路径。将学习的一般路径类比到本节课的学习中。
自主探究 请用相似三角形的学习经验,自主探究相似多边形的相关内容。 通过合作讨论,类比相似三角形的学习方法以及知识,自主探究相似多边形的定义与性质。 用相似三角形的学习模式,自主探究新知,帮助学生建立几何学习的方法和思路。
习得新知 通过类比以及转化的思想得到了相似多边形的定义以及性质。 思考总结 通过类似相似三角形的知识,自主归纳、研究形似多边形的定义与性质,并总结定义与性质的研究方法和思路。
1.提问:请你在生活中找一找,有没有相似多边形吗? 2.总结:对一般的多边形,必须同时满足对应边成比例,对应角相等,但当n固定时,正n边形一定是相似的。 根据定义,寻找相似多变行的实例。通过举例发现,正多边形都是相似的。
应用新知 提问:除了正多边形,还有其他常见的相似多边形吗? 小结:除正多边形外,必须满足对应边成比例,对应角相等两个条件才是相似多边形。 提问:两个矩形不一定相似,那么生活中有常见的相似的矩形吗? 是否能找到长宽比不同的矩形,对折后得到的矩形与原矩形相似? 通过猜想和验证发现,生活中常用的a系列纸都是长宽比为根号2的相似多边形。 我们把由a4纸扩大为a3纸,在改变过程中,保持形状不变的图形改变叫图形的相似。 探究:常用的a系列纸都是长宽比为根号2的相似多边形。在其中选择5张不同大小的,你发现什么有趣的现象?你能给出数学解释吗? 寻找身边的相似多边形,并通过定义,验证是否相似。 研究生活中常见的A3、A4纸具有怎样的性质,从而发现A系列纸的特点。 学生利用五张相似的,但大小不同的纸,自主探究。 通过不同摆放方式,发现长宽比为的矩形相关的结论。 多边形是一个较抽象的概念,通过找生活中的实例,可以让学生直观的感受相似多边形。 通过熟悉的A3、A4纸,引导学生用本节课的方法自主研究这两种纸的性质,发现生活中蕴含的数学知识。
8.数学文化:18世纪,时任哥廷根大学教授的德国学者利希滕贝格发现,一张长宽比为根号2的矩形纸,沿着长边对折,不论折叠几次,折叠后的矩形长宽比都保持不变,得到的矩形也都是相似的。我们把这个比例称为利希滕贝格比例或白银比例。 实际生活中用这个比值设计的纸张能避免生产过程中的浪费。同时,也可以确保将a4纸的图案放大到同系列的纸时图案不会变形。 自主探究:国旗尺寸是由国家标准规定了6个型号.请课后通过查阅资料,研究不同型号的国旗之间是否存在一定的比例关系. 感受数学文化,体会生活中处处有数学。 通过数学文化的渗透,感受生活中处处有数学,而数学最终运用于生活中。 同时,通过课后的探究活动,再次巩固研究图形的一般方法和思路。
总结梳理 回顾整节课,是怎么研究相似多边形的? 思考、小结 类比是几何学习的重要方法。从特殊到一般也是重要的数学思维。 通过小结归纳,帮助学生掌握研究几何图形的一般方法和思路。
当堂检测 1.在如图所示的相似四边形中,求边长x和角度α的大小. 如图,矩形ABCD~矩形BCFE,且AD=AE,求AB:AD. 3.把一个长方形划分成三个全等的长方形(如图).若要使每一个小长方形与原长方形相似,则原长方形应满足什么条件 完成、校对、订正 引导学生自主检测本节课掌握情况.
备注:教学设计应至少含教学目标、教学内容、教学过程等三个部分,如有其它内容,可自行补充增加。
同课章节目录
