5.2 函数 教案(表格式)2023—2024学年浙教版数学八年级上册
文档属性
| 名称 | 5.2 函数 教案(表格式)2023—2024学年浙教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 437.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-27 00:00:00 | ||
图片预览

文档简介
教学设计
课程基本信息
学科 数学 年级 八年级 学期 秋季
课题 5.2 函数(第1课时)
教科书 书 名:义务教育教科书八年级上册数学 出版社:浙江教育出版社
教学目标
1.通过实例,了解函数的概念,感受生活中的数学,会用数学的眼光观察现实世界。 2.理解函数值的概念,在简单情况下求函数值,培养孩子的运算能力。 3.了解函数的三种表示法,感受三者之间的优劣势,三者能互相转换,培养孩子的模型观念。
教学内容
教学重点: 1. 理解函数的定义,能分辨两个变量中,谁是自变量,谁是谁的函数。 2.根据不同的函数表示法确定函数值。 教学难点: 重点:函数的相关概念 2.巩固练习2中的(4)和联系对比环节需要学生真正明白函数的对应关系,变量之间的函数关系不一定是单向的。
教学过程
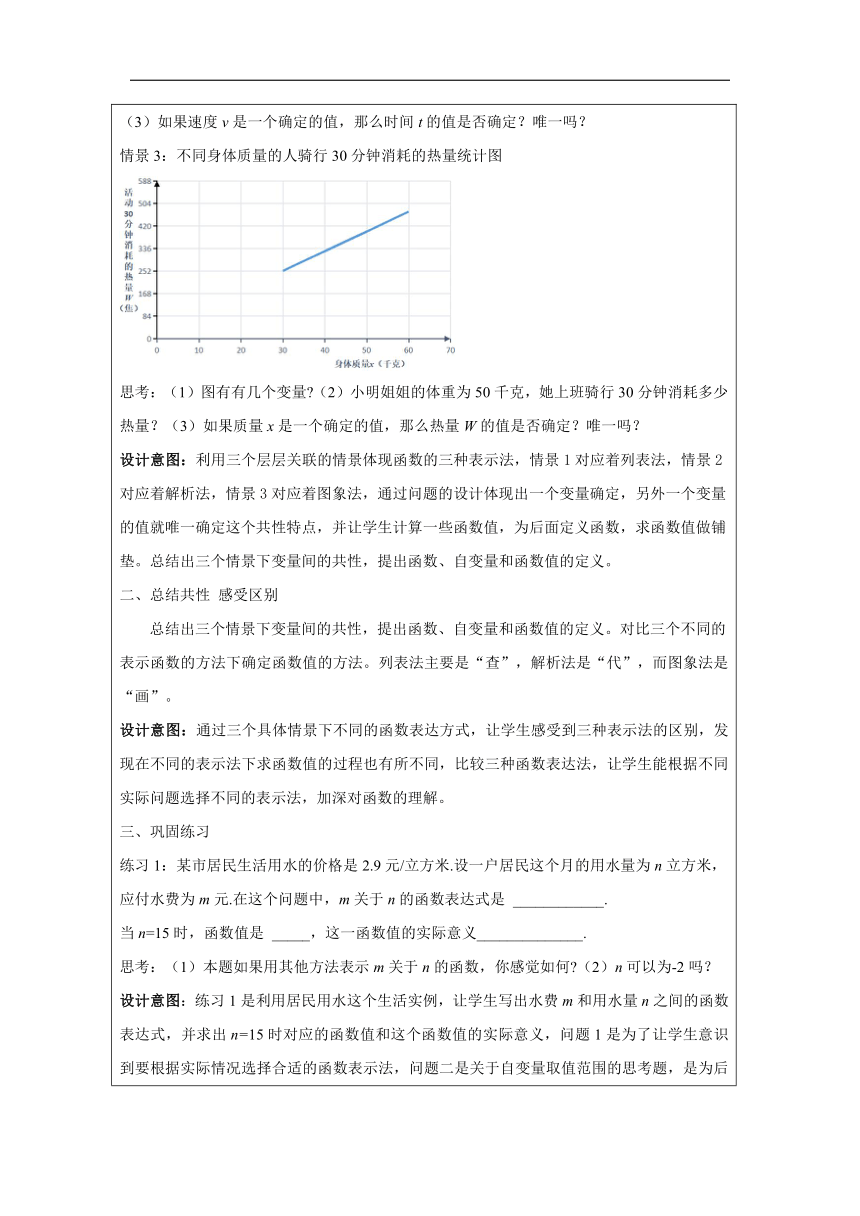
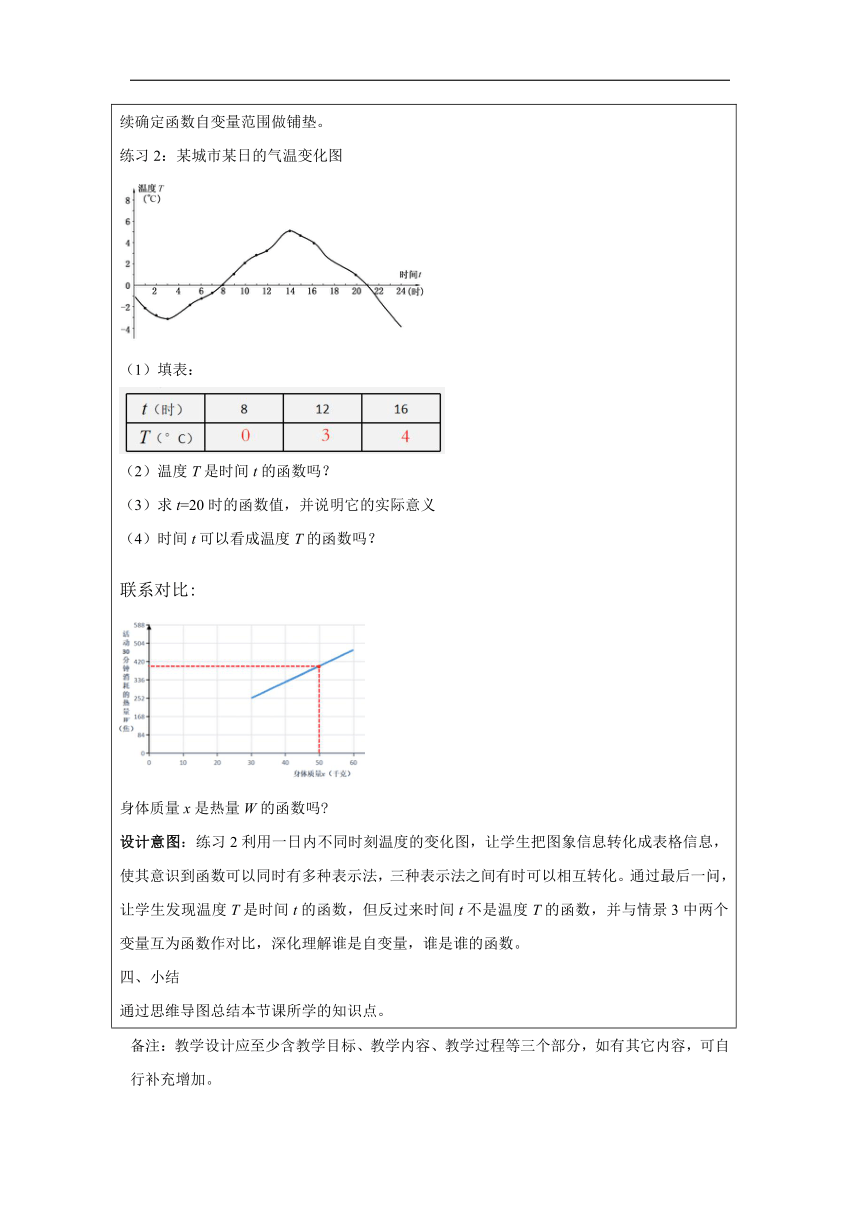
一、探索关系 情景1:小明的姐姐是一名大学生,她利用暑假去一家公司打工,报酬按16元/时计算,设小 明姐姐这个月工作的时间为n小时,应得报酬m元,请填表: 思考:如果时间n是一个确定的值,那么报酬m的值是否确定?唯一吗? 情景2:小明姐姐的家距离公司5400米,她想了解自己在不同出行方式下的上班所需时间, 设不同出行方式的平均速度为v米/分,时间为t分. 思考:(1)请用含v的代数式表示t.(2)计算当v为180、450时,相应的时间t. (3)如果速度v是一个确定的值,那么时间t的值是否确定?唯一吗? 情景3:不同身体质量的人骑行30分钟消耗的热量统计图 思考:(1)图有有几个变量 (2)小明姐姐的体重为50千克,她上班骑行30分钟消耗多少 热量?(3)如果质量x是一个确定的值,那么热量W的值是否确定?唯一吗? 设计意图:利用三个层层关联的情景体现函数的三种表示法,情景1对应着列表法,情景2 对应着解析法,情景3对应着图象法,通过问题的设计体现出一个变量确定,另外一个变量 的值就唯一确定这个共性特点,并让学生计算一些函数值,为后面定义函数,求函数值做铺 垫。总结出三个情景下变量间的共性,提出函数、自变量和函数值的定义。 二、总结共性 感受区别 总结出三个情景下变量间的共性,提出函数、自变量和函数值的定义。对比三个不同的 表示函数的方法下确定函数值的方法。列表法主要是“查”,解析法是“代”,而图象法是“画”。 设计意图:通过三个具体情景下不同的函数表达方式,让学生感受到三种表示法的区别,发现在不同的表示法下求函数值的过程也有所不同,比较三种函数表达法,让学生能根据不同实际问题选择不同的表示法,加深对函数的理解。 三、巩固练习 练习1:某市居民生活用水的价格是2.9元/立方米.设一户居民这个月的用水量为n立方米,应付水费为m元.在这个问题中,m关于n的函数表达式是 ____________. 当n=15时,函数值是 _____,这一函数值的实际意义______________. 思考:(1)本题如果用其他方法表示m关于n的函数,你感觉如何 (2)n可以为-2吗? 设计意图:练习1是利用居民用水这个生活实例,让学生写出水费m和用水量n之间的函数表达式,并求出n=15时对应的函数值和这个函数值的实际意义,问题1是为了让学生意识到要根据实际情况选择合适的函数表示法,问题二是关于自变量取值范围的思考题,是为后续确定函数自变量范围做铺垫。 练习2:某城市某日的气温变化图 (1)填表: (2)温度T是时间t的函数吗? (3)求t=20时的函数值,并说明它的实际意义 (4)时间t可以看成温度T的函数吗? 联系对比: 身体质量x是热量W的函数吗 设计意图:练习2利用一日内不同时刻温度的变化图,让学生把图象信息转化成表格信息,使其意识到函数可以同时有多种表示法,三种表示法之间有时可以相互转化。通过最后一问,让学生发现温度T是时间t的函数,但反过来时间t不是温度T的函数,并与情景3中两个变量互为函数作对比,深化理解谁是自变量,谁是谁的函数。 四、小结 通过思维导图总结本节课所学的知识点。
备注:教学设计应至少含教学目标、教学内容、教学过程等三个部分,如有其它内容,可自行补充增加。
教学设计
课程基本信息
学科 数学 年级 八年级 学期 秋季
课题 5.2 函数(第2课时)
教科书 书 名:义务教育教科书八年级上册数学 出版社:浙江教育出版社 出版日期:2013年7月
教学目标
1.会列简单实际问题中的函数表达式,培养模型观念。 2.会根据函数表达式,已知自变量的值求相应的函数值;或已知函数值,求相应自变量的值。 培养运算能力. 3.能确定简单实际问题中函数自变量的取值范围,培养应用意识。
教学内容
教学重点: 1.求函数的表达式。 2.求函数自变量的取值范围。 教学难点: 1.求自变量的取值范围需要正确理解问题,并化归为解不等式或不等式组。
教学过程
一、温故知新 回顾第1课时的巩固练习1,并利用思考题“n可以为-2吗?”引出新知“函数的自变量 取值范围”的定义。 设计意图:通过回顾复习上节课的巩固练习1,让学生意识到解析法在表示数量关系和确定 函数值上更准确,顺理成章引出这节课均采用解析法来表示函数,并利用思考题引出自变量 是有取值范围的,为后续怎么求自变量的取值范围埋下伏笔。 二、探索新知、讲解例题 1. 求下列函数自变量的取值范围. (1) y=2x+1 (2) 例1.等腰三角形ABC的周长为10,底边BC长为y,腰AB长为x,求: (1)y关于x的函数表达式 (2)自变量x的取值范围 (3)腰长AB=3时,底边的长 思考:当x=6时,y=10-2x的值是多少 对本例有意义吗 当x=2呢 例2 .游泳池应定期换水,某游泳池在一次换水前存水936立方米,换水时打开排水孔,以每小时312立方米的速度将水放出.设放水时间为t小时,游泳池内的存水量为Q立方米. (1)求Q关于t的函数表达式和自变量t的取值范围. (2)放水2小时20分后,游泳池内还剩水多少立方米 (3)放完游泳池内全部水需要多少时间? 例3.如图,每个图形都是由若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≥2)个棋子,设每个团的棋子总数为S. (1)S与n之间能用函数式表示吗 (2)自变量n的取值范围是什么 (3)棋子总数可能是42吗 设计意图:学生明白自变量有取值范围之后,先求自变量在纯粹的函数式中的取值范围,总结出第一个求函数自变量取值范围的条件:自变量需使代数式有意义。再通过三道实际问题例1例2例3总结出第二个求函数自变量取值范围的条件:自变量还需要符合实际。在讲解例题的过程中不仅涉及到求函数值的问题,巩固学生上节课所学的知识,而且突出求自变量的取值范围需要根据实际条件列出不等式或不等式组。 三、总结升华 通过前面的例题,总结出解析法表示函数的基本问题的类别和方法:求函数表达式就是找函数和自变量的等式;求函数的自变量的取值范围就是解不等式或不等式组;已知自变量的值,求相应的函数值就是求代数式的值;已知函数值,求相应自变量的值就是解方程。随后提出函数是刻画现实世界中变化规律的一个重要模型。 设计意图:回顾了前面所有涉及到的实际问题,归纳出解析法表示函数的基本问题的类别和方法,让学生对于函数有一个清晰的认识,意识到函数的重要性和实用性,同时也为后续学习一次函数、二次函数等做铺垫,培养学生的模型意识,能用数学的语言表达现实世界。 四、科普函数历史 简单介绍函数概念的发展史,随后播放关于“函数”一词是如何引入中国的小视频。 设计意图:通过科普关于函数的发展史,体现数学文化的魅力,激起学生学习函数的兴趣,增强课堂的趣味性和内容的丰富性。
备注:教学设计应至少含教学目标、教学内容、教学过程等三个部分,如有其它内容,可自行补充增加。
课程基本信息
学科 数学 年级 八年级 学期 秋季
课题 5.2 函数(第1课时)
教科书 书 名:义务教育教科书八年级上册数学 出版社:浙江教育出版社
教学目标
1.通过实例,了解函数的概念,感受生活中的数学,会用数学的眼光观察现实世界。 2.理解函数值的概念,在简单情况下求函数值,培养孩子的运算能力。 3.了解函数的三种表示法,感受三者之间的优劣势,三者能互相转换,培养孩子的模型观念。
教学内容
教学重点: 1. 理解函数的定义,能分辨两个变量中,谁是自变量,谁是谁的函数。 2.根据不同的函数表示法确定函数值。 教学难点: 重点:函数的相关概念 2.巩固练习2中的(4)和联系对比环节需要学生真正明白函数的对应关系,变量之间的函数关系不一定是单向的。
教学过程
一、探索关系 情景1:小明的姐姐是一名大学生,她利用暑假去一家公司打工,报酬按16元/时计算,设小 明姐姐这个月工作的时间为n小时,应得报酬m元,请填表: 思考:如果时间n是一个确定的值,那么报酬m的值是否确定?唯一吗? 情景2:小明姐姐的家距离公司5400米,她想了解自己在不同出行方式下的上班所需时间, 设不同出行方式的平均速度为v米/分,时间为t分. 思考:(1)请用含v的代数式表示t.(2)计算当v为180、450时,相应的时间t. (3)如果速度v是一个确定的值,那么时间t的值是否确定?唯一吗? 情景3:不同身体质量的人骑行30分钟消耗的热量统计图 思考:(1)图有有几个变量 (2)小明姐姐的体重为50千克,她上班骑行30分钟消耗多少 热量?(3)如果质量x是一个确定的值,那么热量W的值是否确定?唯一吗? 设计意图:利用三个层层关联的情景体现函数的三种表示法,情景1对应着列表法,情景2 对应着解析法,情景3对应着图象法,通过问题的设计体现出一个变量确定,另外一个变量 的值就唯一确定这个共性特点,并让学生计算一些函数值,为后面定义函数,求函数值做铺 垫。总结出三个情景下变量间的共性,提出函数、自变量和函数值的定义。 二、总结共性 感受区别 总结出三个情景下变量间的共性,提出函数、自变量和函数值的定义。对比三个不同的 表示函数的方法下确定函数值的方法。列表法主要是“查”,解析法是“代”,而图象法是“画”。 设计意图:通过三个具体情景下不同的函数表达方式,让学生感受到三种表示法的区别,发现在不同的表示法下求函数值的过程也有所不同,比较三种函数表达法,让学生能根据不同实际问题选择不同的表示法,加深对函数的理解。 三、巩固练习 练习1:某市居民生活用水的价格是2.9元/立方米.设一户居民这个月的用水量为n立方米,应付水费为m元.在这个问题中,m关于n的函数表达式是 ____________. 当n=15时,函数值是 _____,这一函数值的实际意义______________. 思考:(1)本题如果用其他方法表示m关于n的函数,你感觉如何 (2)n可以为-2吗? 设计意图:练习1是利用居民用水这个生活实例,让学生写出水费m和用水量n之间的函数表达式,并求出n=15时对应的函数值和这个函数值的实际意义,问题1是为了让学生意识到要根据实际情况选择合适的函数表示法,问题二是关于自变量取值范围的思考题,是为后续确定函数自变量范围做铺垫。 练习2:某城市某日的气温变化图 (1)填表: (2)温度T是时间t的函数吗? (3)求t=20时的函数值,并说明它的实际意义 (4)时间t可以看成温度T的函数吗? 联系对比: 身体质量x是热量W的函数吗 设计意图:练习2利用一日内不同时刻温度的变化图,让学生把图象信息转化成表格信息,使其意识到函数可以同时有多种表示法,三种表示法之间有时可以相互转化。通过最后一问,让学生发现温度T是时间t的函数,但反过来时间t不是温度T的函数,并与情景3中两个变量互为函数作对比,深化理解谁是自变量,谁是谁的函数。 四、小结 通过思维导图总结本节课所学的知识点。
备注:教学设计应至少含教学目标、教学内容、教学过程等三个部分,如有其它内容,可自行补充增加。
教学设计
课程基本信息
学科 数学 年级 八年级 学期 秋季
课题 5.2 函数(第2课时)
教科书 书 名:义务教育教科书八年级上册数学 出版社:浙江教育出版社 出版日期:2013年7月
教学目标
1.会列简单实际问题中的函数表达式,培养模型观念。 2.会根据函数表达式,已知自变量的值求相应的函数值;或已知函数值,求相应自变量的值。 培养运算能力. 3.能确定简单实际问题中函数自变量的取值范围,培养应用意识。
教学内容
教学重点: 1.求函数的表达式。 2.求函数自变量的取值范围。 教学难点: 1.求自变量的取值范围需要正确理解问题,并化归为解不等式或不等式组。
教学过程
一、温故知新 回顾第1课时的巩固练习1,并利用思考题“n可以为-2吗?”引出新知“函数的自变量 取值范围”的定义。 设计意图:通过回顾复习上节课的巩固练习1,让学生意识到解析法在表示数量关系和确定 函数值上更准确,顺理成章引出这节课均采用解析法来表示函数,并利用思考题引出自变量 是有取值范围的,为后续怎么求自变量的取值范围埋下伏笔。 二、探索新知、讲解例题 1. 求下列函数自变量的取值范围. (1) y=2x+1 (2) 例1.等腰三角形ABC的周长为10,底边BC长为y,腰AB长为x,求: (1)y关于x的函数表达式 (2)自变量x的取值范围 (3)腰长AB=3时,底边的长 思考:当x=6时,y=10-2x的值是多少 对本例有意义吗 当x=2呢 例2 .游泳池应定期换水,某游泳池在一次换水前存水936立方米,换水时打开排水孔,以每小时312立方米的速度将水放出.设放水时间为t小时,游泳池内的存水量为Q立方米. (1)求Q关于t的函数表达式和自变量t的取值范围. (2)放水2小时20分后,游泳池内还剩水多少立方米 (3)放完游泳池内全部水需要多少时间? 例3.如图,每个图形都是由若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≥2)个棋子,设每个团的棋子总数为S. (1)S与n之间能用函数式表示吗 (2)自变量n的取值范围是什么 (3)棋子总数可能是42吗 设计意图:学生明白自变量有取值范围之后,先求自变量在纯粹的函数式中的取值范围,总结出第一个求函数自变量取值范围的条件:自变量需使代数式有意义。再通过三道实际问题例1例2例3总结出第二个求函数自变量取值范围的条件:自变量还需要符合实际。在讲解例题的过程中不仅涉及到求函数值的问题,巩固学生上节课所学的知识,而且突出求自变量的取值范围需要根据实际条件列出不等式或不等式组。 三、总结升华 通过前面的例题,总结出解析法表示函数的基本问题的类别和方法:求函数表达式就是找函数和自变量的等式;求函数的自变量的取值范围就是解不等式或不等式组;已知自变量的值,求相应的函数值就是求代数式的值;已知函数值,求相应自变量的值就是解方程。随后提出函数是刻画现实世界中变化规律的一个重要模型。 设计意图:回顾了前面所有涉及到的实际问题,归纳出解析法表示函数的基本问题的类别和方法,让学生对于函数有一个清晰的认识,意识到函数的重要性和实用性,同时也为后续学习一次函数、二次函数等做铺垫,培养学生的模型意识,能用数学的语言表达现实世界。 四、科普函数历史 简单介绍函数概念的发展史,随后播放关于“函数”一词是如何引入中国的小视频。 设计意图:通过科普关于函数的发展史,体现数学文化的魅力,激起学生学习函数的兴趣,增强课堂的趣味性和内容的丰富性。
备注:教学设计应至少含教学目标、教学内容、教学过程等三个部分,如有其它内容,可自行补充增加。
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
