第3章 一元二次方程 项目化学习题集(含答案) 2023—2024学年浙教版数学八年级上册
文档属性
| 名称 | 第3章 一元二次方程 项目化学习题集(含答案) 2023—2024学年浙教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-27 10:11:52 | ||
图片预览




文档简介
浙教版八年级下册一元二次方程-项目化学习题集
资料介绍:
近几年,中考题中出现了一些不一样的情境类试题,考题围绕学生的生活实际设问,问题的解决需要建立数学模型,进而解决实际问题。而试题最大特点就是试题的结构“项目化”,呈现方式有别以往的“实际问题”,我们姑且称之为“项目化试题”吧。如温州中考,金华中考等
中考命题是我们平时考试的导向,所以在初二的期中期末中也出现了很多的项目化试题
“项目化学习”试题特点
以真实问题情境为载体命题立意、情境创设、任务指向与评分标准是命题的四大基本要素,四者相辅相成、不可分割。情境是命题立意与任务指向之间的桥梁和纽带,情境的真实性是项目化学习试题的重要特征。当然,这里的真实性是指所学知识和能力的真实及所运用思维方式的真实。
以驱动性问题为核心驱动性问题使整个项目活动始终保持持续性和一致性,是项目化学习的核心要素。项目化学习的驱动性问题一般是从一个大问题开始,逐步分解,层层递进,形成金字塔式的结构化问题链。学生正是在不断分析问题与解决问题的过程中,促使自己的认识持续深化、理解渐次深刻、情感不断升华、素养有效提升。
以核心知识为支撑项目化学习通过项目或活动使学生理解与掌握相应的核心知识。这要求项目化学习试题的命题者在精心研读课程标准、教材等基础上,寻找并确定核心知识,有机融入相应项目或活动中,融情感态度价值观、能力、知识于一体,以促成核心素养的有效落地。
(四)以高阶思维为目标美国教育心理学家L.W.安德森等继承与发展了教育心理学家本杰明·布鲁姆的教育目标分类学理论,将教育目标分为认知过程维度和知识维度。其中,认知过程维度包括记忆、理解、运用、分析、评价、创造六个类目。这六个类目由低到高、由简及繁,梯度排列。项目化学习往往设计富有挑战性的问题,创设富含高阶思维的真实学习情境,激发学生探究学习的兴趣与动力,提出带有问题分析、创造等高阶思维的项目任务,引导学生通过合作探究转化成项目化学习成果。
来上题!
试题
1.
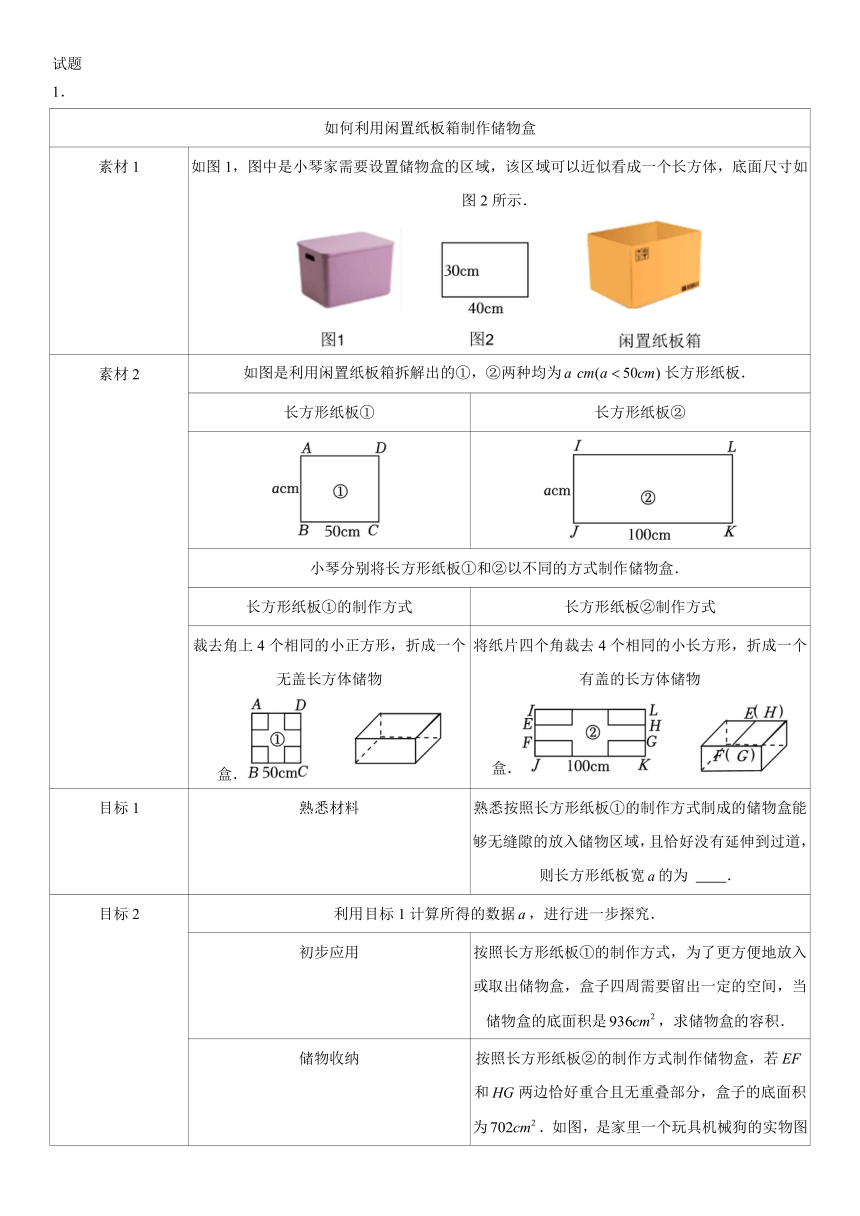
如何利用闲置纸板箱制作储物盒
素材1 如图1,图中是小琴家需要设置储物盒的区域,该区域可以近似看成一个长方体,底面尺寸如图2所示.
素材2 如图是利用闲置纸板箱拆解出的①,②两种均为长方形纸板.
长方形纸板① 长方形纸板②
小琴分别将长方形纸板①和②以不同的方式制作储物盒.
长方形纸板①的制作方式 长方形纸板②制作方式
裁去角上4个相同的小正方形,折成一个无盖长方体储物盒. 将纸片四个角裁去4个相同的小长方形,折成一个有盖的长方体储物盒.
目标1 熟悉材料 熟悉按照长方形纸板①的制作方式制成的储物盒能够无缝隙的放入储物区域,且恰好没有延伸到过道,则长方形纸板宽的为 .
目标2 利用目标1计算所得的数据,进行进一步探究.
初步应用 按照长方形纸板①的制作方式,为了更方便地放入或取出储物盒,盒子四周需要留出一定的空间,当储物盒的底面积是,求储物盒的容积.
储物收纳 按照长方形纸板②的制作方式制作储物盒,若和两边恰好重合且无重叠部分,盒子的底面积为.如图,是家里一个玩具机械狗的实物图和尺寸大小,请通过计算判断玩具机械狗能否完全放入该储物盒.
2.根据以下素材,探索完成任务.
圆柱体外包装的材料损耗率问题研究
素材1 厂商在生产产品时,对产品外包装的材料,通常要考虑尽可能地合理利用,减少浪费.圆柱体形状的物品,它的外包装盒通常都是长方体,且上下底面为正方形.
素材2 设计产品外包装时,我们把裁剪掉的废料部分的面积与原图形的面积之比称为材料的损耗率.一种材料利用率较高的裁剪方式如图所示,采用正方形纸板裁剪,只需剪掉四条边上的四个小三角形. 按这种方式包装一个底面直径为2,高为1的圆柱体(接缝处的材料损耗不计),损耗率只有.
问题解决
任务1 现采用一张边长为的正方形纸,按如图所示的裁剪方式剪掉各边上的四个三角形后,可恰好无缝地做成一个圆柱体的外包装盒.设圆柱体的底面半径为,则它的高 (用的代数式表示).
任务2 在图中,若已知该圆柱体外包装盒的材料损耗率为,求这个圆柱体的底面半径.
任务3 现利用两块同样大小的正方形纸板,按如图方式裁剪后,可包装两个高分别为4和2的圆柱体,发现这两个圆柱体的体积恰好相等.求第一个圆柱体的底面半径.(圆柱体的体积底面积高)
3.根据以下素材,探索完成任务.
素材1 某校统一安装了日光灯,日光灯中最易损坏的是灯管和镇流器.
素材2 该校后勤部准备补进灯管和镇流器共400件.批发市场灯管的单价为30元,镇流器的单价为80元.商家为了促销且保证有一定的利润,当镇流器购买数量超过80件时,每多购买1件,单价下降1元,但单价不低于50元.
问题解决
任务1 若镇流器补进90件,则学校补进镇流器和灯管共多少元?
任务2 设镇流器补进件,若,刚补进镇流器的单价为 元,补进灯管的总价为 (用含的代数式表示);
任务3 若学校后勤部补进镇流器和灯管共花15000元,求补进镇流器多少件?
4.根据以下信息,探索完成任务.
如何设计种植方案?
素材1 小明以“种植农作物”为主题在自己家100平方米的土地上进行课外实践,现有、两种作物的相关信息如下表所示: 作物作物每平方米种植株树(株210单株产量(千克)1.20.5
素材2 由于作物植株间距较大,可增加作物每平方米的种植株树.经过调研发现,每平方米种植作物每增加1株,作物的单株产量减少0.1千克.
素材3 若同时种植、两种作物,实行分区域种植.
问题解决
单一种植(全部种植作物) 任务1:明确数量关系 设每平方米增加株作物为正整数),则每平方米有 株,单株产量为 千克. (用含的代数式表示)
任务2:计算产量 要使作物每平方米产量为4.8千克,则每平方米应种植多少株?
分区种植(种植、两种作物) 任务3:规划种植方案 设这100平方米的土地中有平方米用于种植作物,且每平方米产量最大,其余区域按照每平方米10株种植作物,当这100平方米总产量不低于496千克时,则的取值范围是
5.根据以下素材,探索完成任务.
素材1 定义:如图1,点将线段分成两部分,如果,那么点称为线段的黄金分割点.
素材2 某兴趣小组在进行研究性学习时,由黄金分割点联想到“黄金分割线”,类似地给出黄金分割线的定义:直线将一个面积为的图形分成面积分别为,的两部分,如果,那么直线称为该图形的黄金分割线.
素材3 平行四边形是中心对称图形:在同一平面内,一个三角形绕其中一边的中点旋转,其余两边与旋转后相对应的两边组成一个平行四边形,例如,图2中的绕的中点旋转后与原三角形组成一个平行四边形(如图.
问题解决
任务1 问题1:如图3,边上黄金分割点旋转后的对称点是否也是边上的黄金分割点?请写出你的判断结论,并说明理由. 问题2:直线是不是四边形的黄金分割线?请写出你的判断结论: .
任务2 请在图3探索:边上是否存在点,使得直线是四边形的黄金分割线?如果存在,请说明点的位置;如果不存在,请说明理由.
任务3 兴趣小组探索图2时猜想:在中,若点为边上的黄金分割点,连接,则直线是的黄金分割线,你认为对吗?为什么?
任务4 兴趣小组探索图2时还发现:若点是的边的黄金分割点,过点任意作一条直线交于点,再过点作交于点,则直线是的黄金分割线,请你给出证明.
6.
如何裁剪出符合要求的长方形纸片?
素材1 如图1,是腰长为的等腰直角三角形卡纸,校艺术节上,甲、乙、丙三名同学分别用这样的卡纸试图裁剪出不一样的长方形纸片,并使长方形的四个顶点都在的边上.
素材2 甲同学按图2的方式裁剪,想裁出面积为三角形面积的的长方形纸片,乙同学按图3的方式裁剪,想裁出面积为三角形面积的的长方形纸片,丙同学想裁出面积最大的长方形纸片.
任务1 计算纸片周长 请帮甲同学计算此长方形纸片的周长.
任务2 判断裁剪方案 请帮乙同学判断此裁剪方案是否能够实现,说明理由.
任务3 计算最大面积 请帮丙同学计算出长方形纸片面积的最大值.
7.根据以下销售情况,解决销售任务.
销售情况分析
总公司将一批衬衫由甲、乙两家分店共同销售,因地段不同,它们的销售情况如下:
店面 甲店 乙店
日销售情况 每天可售出20件,每件盈利40元. 每天可售出32件,每件盈利30元.
市场调查 经调查发现,每件衬衫每降价1元,甲、乙两家店一天都可多售出2件.
情况设置 设甲店每件衬衫降价元,乙店每件衬衫降价元.
任务解决
任务1 甲店每天的销售量 (用含的代数式表示). 乙店每天的销售量 (用含的代数式表示).
任务2 当,时,分别求出甲、乙店每天的盈利.
任务3 总公司规定两家分店下降的价格必须相同,请求出每件衬衫下降多少元时,两家分店一天的盈利和为2244元.
8.
如何设计计算油漆用量的方案?
素材1 小明家的一面墙壁由边长为1分米的小正方形密铺而成,上面画了如图所示的心形图案.他现在准备将心形图案的内部刷上红色的油漆,已知刷1平方分米需要0.02升的油漆. 图1
素材2 奥地利数学家皮克证明了格点多边形的面积公式,格点多边形的面积与格点多边形内的格点数和边界上的格点数有关,面积公式可表示为(其中,为常数). 示例:如图2,格点多边形内的格点数,边界上的格点数,格点多边形的面积. 图2
问题解决
任务1 在图3中画一个格点多边形,并计算它的格点多边形内的格点数,边界上的格点数和面积. ; ; . 图3
任务2 得出格点多边形的面积公式 根据图2和图3的数据,求常数,的值.
任务3 计算油漆的用量 求需要红色油漆多少升?
9.根据以下素材,完成探索任务.
探索果园土地规划和销售利润问题
素材1 某农户承包了一块长方形果园,图1是果园的平面图,其中米,米.准备在它的四周铺设道路,上下两条横向道路的宽度都为米,左右两条纵向道路的宽度都为米,中间部分种植水果.已知道路的路面造价是50元;出于货车通行等因素的考虑,道路宽度不超过12米,且不小于5米.
素材2 该农户发现某一种草莓销售前景比较不错,经市场调查,草莓培育一年可产果,已知每平方米的草莓销售平均利润为100元;果园每年的承包费为25万元,期间需一次性投入33万元购进新苗,每年还需25万元的养护、施肥、运输等其余费用.
问题解决
任务1 解决果园中路面宽度的设计对种植面积的影响. (1)请直接写出纵向道路宽度的取值范围. (2)若中间种植的面积是,则路面设置的宽度是否符合要求.
任务2 解决果园种植的预期利润问题.(净利润草莓销售的总利润路面造价费用果园承包费用新苗购置费用其余费用) (3)经过1年后,农户是否可以达到预期净利润400万元?请说明理由.
10.根据以下素材,探索完成任务.
如何估算游客人数和门票收入?
素材1 今年疫情开放以来,我县接待的游客人数逐月增加,据统计,游玩某景区的游客人数1月份为4万人,3月份为5.76万人.
素材2 若该景区仅有,两个景点,售票处出示的三种购票方式如表所示: 据预测,5月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万.并且当甲、乙两种门票价格不变时,丙种门票价格每下降1元,将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票. 购票方式 甲 乙 丙
可游玩景点 和
门票价格 100元人 80元人 160元人
问题解决
任务1 确定增长率 求2月和3月这两个月中,该景区游客人数平均每月增长百分之几.
任务2 预计门票收入 若丙种门票价格下降10元,求景区5月份的门票总收入.
任务3 拟定价格方案 将丙种门票价格下降多少元时,景区5月份的门票总收入有816万元?
11.综合实践:
项目主题 “亚运主题”草坪设计
项目情境 为了迎亚会,同学们参与一块长为40米,宽为30米的矩形“亚运主题”草 坪方案设计的项目学习.以下为项目学习小组对草坪设计的研究过程.
活动任务一 请设计两条相同宽度的小路连接矩形草坪两组对边.小组内同学们设计的方案主要有甲、乙、丙、丁四种典型的方案
驱动问题一 (1)项目小组设计出来的四种方案小路面积的大小关系? ①直观猜想:我认为 ; 请用简洁的语言或代数式表达你的猜想) ②具体验证:选择最简单的甲、乙方案,假设小路宽为1米,则甲、乙方案中小路的面积分别为 和 ; ③一般验证:若小路宽为米,则甲、乙方案中小路所占的面积分别为 和 .
活动任务二 为施工方便,学校选择甲种方案设计,并要求除小路后草坪面积约为1064平方米.
驱动问题二 (2)请计算两条小路的宽度是多少?
活动任务三 为了布置五环标志等亚运元素,将在草坪上的亚运宣传主题墙前,用篱笆围(三边) 成面积为100平方米的矩形,如图.
驱动问题三 (3)为了使篱笆恰好用完同时围住三面,项目小组的同学对下列问题展开探究,其中矩形宽,长. ①若30米长的篱笆,请用两种不同的函数表示关于的函数关系. ②数学之星小明提出一个问题:若米长的篱笆恰好用完,且有两种不同方案可以选择,使得两种方案的宽之和小于15米,甲同学说“篱笆的长可以是28米”,乙同学说“篱笆的长可以是32米”,你认为他们俩的说法对吗?请说明理由.
【初二下专题4】项目化学习(PBL)类问题
参考答案与试题解析
1.(1)解:储物区域的长为,由于收纳盒可以完全放入储物区域,
则图1中的四角裁去小正方形的边长为,
则收纳盒的宽小正方形的边长,
由图2知,设小正方形的边长为,
由题意可得:,
解得:,
体积为,
答:储物盒的容积为6552立方厘米;
(2)设小长方形的宽为,,长为,
由题意可得:,
解得:
小长方形的宽为
当,之间两边恰好重合且无重叠部分,收纳盒的高为,
玩具机械狗也不能完全放入该储物;
综上所述:玩具机械狗不能完全放入该储物.
答:玩具机械狗不能完全放入该储物.
2.(1)解:由正方形的对角线的性质,边长为,对角线的一半为;
圆柱体的底面半径为,所以它的高.
(2)解裁剪掉的废料部分的面积与原图形的面积之比称为材料的损耗率,
裁剪掉的废料部分的面积,原图形的面积,
所以列方程为:.
解得.
由,得.
得.
答:这个圆柱体的底面半径为1.2.
(3)设两个圆柱的底面半径分别为和,则有,
得,
由题意,得
解得,(不合题意,舍去),
答:第一个圆柱体的底面半径为.
3.解:任务1:依题意,镇流器补进90件,学校补进镇流器和灯管共元,
答:若镇流器补进90件,则学校补进镇流器和灯管共15600元,
任务2:设镇流器补进件,若,刚补进镇流器的单价为(元,
补进灯管的总价为:(元,
故答案为:;.
任务3:依题意,,
解得:,,
.
.
当时,
依题意,,
解得:,
当时,镇流器的单价固定为50元,
,
.
答:补进镇流器100件或60件或150件.
4.解:任务一:设每平方米增加株作物为正整数),则每平方米有株,单株产量为千克,
故答案为:,;
任务二:根据题意得:,
整理得:,
解得:,,
或,
答:每平方米应种植6株或8株;
任务三:设种植作物每平方米的产量为千克,
根据题意得:,
,
当时,有最大值,最大值为4.9,
种植作物每平方米最大产量为1.9千克,
根据题意得:,
解得,
则的取值范围是,
故答案为:.
5.解:任务
问题
点是的黄金分割点,理由如下:
由旋转可得:,,,
为的黄金分割点,
,
,
点是上的黄金分割点;
问题
直线不是四边形的黄金分割线,
故答案为:直线不是四边形的黄金分割线;
任务
边上存在点,使得直线是四边形的黄金分割线,
过点作交于点,则是四边形的黄金分割线,
如图:
点即为所求的点;
任务
正确,理由如下:
如图:
是的黄金分割点,
,
,,
,
是三角形的黄金分割线;
任务
证明:连接,如图:
,
,,
,,
点是的边的黄金分割点,
,
,
,
直线是的黄金分割线.
6.解:任务1.由题意得:,
,
.
设,则,
矩形的面积为三角形面积的,
,
化简得,
解得:或,
矩形的边长为,,
周长为;
任务2.由题意得:,,
,,
.
设,则,
矩形的面积为三角形面积的,
,
整理得:.
△,
方程无实数根,
乙同学的方案不能实现;
任务3.图2方案:,
当时,矩形的面积最大为;
图3方案:,
当 时,面积最大为,
长方形纸片面积的最大值为.
7.解:任务1,甲店每天的销售量为件,乙店每天的销售量为件,
故答案为:件,件;
任务2,当时,甲店每天的盈利为(元;
当时,乙店每天的盈利为(元;
任务3,设每件衬衫下降元时,两家分店一天的盈利和为2244元,
由题意得:,
整理得:,
解得:,
即每件衬衫下降11元时,两家分店一天的盈利和为2244元.
8.
解:任务一:如图,即为所求.
观察图象可知:,,,
故答案为:1,8,4;
任务二:由题意,,
解得,
;
任务三:由题意,,,
,
(升.
9.解:(1)道路宽度不超过12米,且不小于5米,
纵向道路宽度的取值范围为;
(2)根据题意得:,
整理得:,
解得:,,
,
符合题意,
路面设置的宽度符合要求;
(3)经过1年后,农户可以达到预期净利润400万元,理由如下:
假设经过1年后,农户可以达到预期净利润400万元,
根据题意得:,
整理得:,
解得:,,
又,
符合题意,
假设成立,
即经过1年后,农户可以达到预期净利润400万元.
10.解:(任务设2月和3月这两个月中,该景区游客人数平均每月增长率为,
根据题意得:,
解得:,(不符合题意,舍去).
答:2月和3月这两个月中,该景区游客人数平均每月增长;
(任务根据题意得:
(元,
7980000元万元.
答:景区5月份的门票总收入798万元;
(任务设丙种门票价格下降元时,景区5月份的门票总收入有816万元,
根据题意得:,
整理得:,
解得:,.
答:丙种门票价格下降20元或28元时,景区5月份的门票总收入有816万元.
【点评】本题考查了一元二次方程的应用以及有理数的混合运算,找准等量关系,正确列出一元二次方程是解题的关键.
11.解:(1)①直观猜想:我认为:四种方案小路面积的大小相等,
故答案为:四种方案小路面积的大小相等;
②甲:;
乙:,
故答案为:,;
③甲:,
乙:,
故答案为:,;
(2)设小路的宽为,则,
解得:或(不合题意,舍去),
答:小路的宽为;
(3)①方法,,
方法,;
②由题意得:,
设方程的两个根分别为,,则,且△,
则:,,
,
,
故甲和乙的说法都不正确.
资料介绍:
近几年,中考题中出现了一些不一样的情境类试题,考题围绕学生的生活实际设问,问题的解决需要建立数学模型,进而解决实际问题。而试题最大特点就是试题的结构“项目化”,呈现方式有别以往的“实际问题”,我们姑且称之为“项目化试题”吧。如温州中考,金华中考等
中考命题是我们平时考试的导向,所以在初二的期中期末中也出现了很多的项目化试题
“项目化学习”试题特点
以真实问题情境为载体命题立意、情境创设、任务指向与评分标准是命题的四大基本要素,四者相辅相成、不可分割。情境是命题立意与任务指向之间的桥梁和纽带,情境的真实性是项目化学习试题的重要特征。当然,这里的真实性是指所学知识和能力的真实及所运用思维方式的真实。
以驱动性问题为核心驱动性问题使整个项目活动始终保持持续性和一致性,是项目化学习的核心要素。项目化学习的驱动性问题一般是从一个大问题开始,逐步分解,层层递进,形成金字塔式的结构化问题链。学生正是在不断分析问题与解决问题的过程中,促使自己的认识持续深化、理解渐次深刻、情感不断升华、素养有效提升。
以核心知识为支撑项目化学习通过项目或活动使学生理解与掌握相应的核心知识。这要求项目化学习试题的命题者在精心研读课程标准、教材等基础上,寻找并确定核心知识,有机融入相应项目或活动中,融情感态度价值观、能力、知识于一体,以促成核心素养的有效落地。
(四)以高阶思维为目标美国教育心理学家L.W.安德森等继承与发展了教育心理学家本杰明·布鲁姆的教育目标分类学理论,将教育目标分为认知过程维度和知识维度。其中,认知过程维度包括记忆、理解、运用、分析、评价、创造六个类目。这六个类目由低到高、由简及繁,梯度排列。项目化学习往往设计富有挑战性的问题,创设富含高阶思维的真实学习情境,激发学生探究学习的兴趣与动力,提出带有问题分析、创造等高阶思维的项目任务,引导学生通过合作探究转化成项目化学习成果。
来上题!
试题
1.
如何利用闲置纸板箱制作储物盒
素材1 如图1,图中是小琴家需要设置储物盒的区域,该区域可以近似看成一个长方体,底面尺寸如图2所示.
素材2 如图是利用闲置纸板箱拆解出的①,②两种均为长方形纸板.
长方形纸板① 长方形纸板②
小琴分别将长方形纸板①和②以不同的方式制作储物盒.
长方形纸板①的制作方式 长方形纸板②制作方式
裁去角上4个相同的小正方形,折成一个无盖长方体储物盒. 将纸片四个角裁去4个相同的小长方形,折成一个有盖的长方体储物盒.
目标1 熟悉材料 熟悉按照长方形纸板①的制作方式制成的储物盒能够无缝隙的放入储物区域,且恰好没有延伸到过道,则长方形纸板宽的为 .
目标2 利用目标1计算所得的数据,进行进一步探究.
初步应用 按照长方形纸板①的制作方式,为了更方便地放入或取出储物盒,盒子四周需要留出一定的空间,当储物盒的底面积是,求储物盒的容积.
储物收纳 按照长方形纸板②的制作方式制作储物盒,若和两边恰好重合且无重叠部分,盒子的底面积为.如图,是家里一个玩具机械狗的实物图和尺寸大小,请通过计算判断玩具机械狗能否完全放入该储物盒.
2.根据以下素材,探索完成任务.
圆柱体外包装的材料损耗率问题研究
素材1 厂商在生产产品时,对产品外包装的材料,通常要考虑尽可能地合理利用,减少浪费.圆柱体形状的物品,它的外包装盒通常都是长方体,且上下底面为正方形.
素材2 设计产品外包装时,我们把裁剪掉的废料部分的面积与原图形的面积之比称为材料的损耗率.一种材料利用率较高的裁剪方式如图所示,采用正方形纸板裁剪,只需剪掉四条边上的四个小三角形. 按这种方式包装一个底面直径为2,高为1的圆柱体(接缝处的材料损耗不计),损耗率只有.
问题解决
任务1 现采用一张边长为的正方形纸,按如图所示的裁剪方式剪掉各边上的四个三角形后,可恰好无缝地做成一个圆柱体的外包装盒.设圆柱体的底面半径为,则它的高 (用的代数式表示).
任务2 在图中,若已知该圆柱体外包装盒的材料损耗率为,求这个圆柱体的底面半径.
任务3 现利用两块同样大小的正方形纸板,按如图方式裁剪后,可包装两个高分别为4和2的圆柱体,发现这两个圆柱体的体积恰好相等.求第一个圆柱体的底面半径.(圆柱体的体积底面积高)
3.根据以下素材,探索完成任务.
素材1 某校统一安装了日光灯,日光灯中最易损坏的是灯管和镇流器.
素材2 该校后勤部准备补进灯管和镇流器共400件.批发市场灯管的单价为30元,镇流器的单价为80元.商家为了促销且保证有一定的利润,当镇流器购买数量超过80件时,每多购买1件,单价下降1元,但单价不低于50元.
问题解决
任务1 若镇流器补进90件,则学校补进镇流器和灯管共多少元?
任务2 设镇流器补进件,若,刚补进镇流器的单价为 元,补进灯管的总价为 (用含的代数式表示);
任务3 若学校后勤部补进镇流器和灯管共花15000元,求补进镇流器多少件?
4.根据以下信息,探索完成任务.
如何设计种植方案?
素材1 小明以“种植农作物”为主题在自己家100平方米的土地上进行课外实践,现有、两种作物的相关信息如下表所示: 作物作物每平方米种植株树(株210单株产量(千克)1.20.5
素材2 由于作物植株间距较大,可增加作物每平方米的种植株树.经过调研发现,每平方米种植作物每增加1株,作物的单株产量减少0.1千克.
素材3 若同时种植、两种作物,实行分区域种植.
问题解决
单一种植(全部种植作物) 任务1:明确数量关系 设每平方米增加株作物为正整数),则每平方米有 株,单株产量为 千克. (用含的代数式表示)
任务2:计算产量 要使作物每平方米产量为4.8千克,则每平方米应种植多少株?
分区种植(种植、两种作物) 任务3:规划种植方案 设这100平方米的土地中有平方米用于种植作物,且每平方米产量最大,其余区域按照每平方米10株种植作物,当这100平方米总产量不低于496千克时,则的取值范围是
5.根据以下素材,探索完成任务.
素材1 定义:如图1,点将线段分成两部分,如果,那么点称为线段的黄金分割点.
素材2 某兴趣小组在进行研究性学习时,由黄金分割点联想到“黄金分割线”,类似地给出黄金分割线的定义:直线将一个面积为的图形分成面积分别为,的两部分,如果,那么直线称为该图形的黄金分割线.
素材3 平行四边形是中心对称图形:在同一平面内,一个三角形绕其中一边的中点旋转,其余两边与旋转后相对应的两边组成一个平行四边形,例如,图2中的绕的中点旋转后与原三角形组成一个平行四边形(如图.
问题解决
任务1 问题1:如图3,边上黄金分割点旋转后的对称点是否也是边上的黄金分割点?请写出你的判断结论,并说明理由. 问题2:直线是不是四边形的黄金分割线?请写出你的判断结论: .
任务2 请在图3探索:边上是否存在点,使得直线是四边形的黄金分割线?如果存在,请说明点的位置;如果不存在,请说明理由.
任务3 兴趣小组探索图2时猜想:在中,若点为边上的黄金分割点,连接,则直线是的黄金分割线,你认为对吗?为什么?
任务4 兴趣小组探索图2时还发现:若点是的边的黄金分割点,过点任意作一条直线交于点,再过点作交于点,则直线是的黄金分割线,请你给出证明.
6.
如何裁剪出符合要求的长方形纸片?
素材1 如图1,是腰长为的等腰直角三角形卡纸,校艺术节上,甲、乙、丙三名同学分别用这样的卡纸试图裁剪出不一样的长方形纸片,并使长方形的四个顶点都在的边上.
素材2 甲同学按图2的方式裁剪,想裁出面积为三角形面积的的长方形纸片,乙同学按图3的方式裁剪,想裁出面积为三角形面积的的长方形纸片,丙同学想裁出面积最大的长方形纸片.
任务1 计算纸片周长 请帮甲同学计算此长方形纸片的周长.
任务2 判断裁剪方案 请帮乙同学判断此裁剪方案是否能够实现,说明理由.
任务3 计算最大面积 请帮丙同学计算出长方形纸片面积的最大值.
7.根据以下销售情况,解决销售任务.
销售情况分析
总公司将一批衬衫由甲、乙两家分店共同销售,因地段不同,它们的销售情况如下:
店面 甲店 乙店
日销售情况 每天可售出20件,每件盈利40元. 每天可售出32件,每件盈利30元.
市场调查 经调查发现,每件衬衫每降价1元,甲、乙两家店一天都可多售出2件.
情况设置 设甲店每件衬衫降价元,乙店每件衬衫降价元.
任务解决
任务1 甲店每天的销售量 (用含的代数式表示). 乙店每天的销售量 (用含的代数式表示).
任务2 当,时,分别求出甲、乙店每天的盈利.
任务3 总公司规定两家分店下降的价格必须相同,请求出每件衬衫下降多少元时,两家分店一天的盈利和为2244元.
8.
如何设计计算油漆用量的方案?
素材1 小明家的一面墙壁由边长为1分米的小正方形密铺而成,上面画了如图所示的心形图案.他现在准备将心形图案的内部刷上红色的油漆,已知刷1平方分米需要0.02升的油漆. 图1
素材2 奥地利数学家皮克证明了格点多边形的面积公式,格点多边形的面积与格点多边形内的格点数和边界上的格点数有关,面积公式可表示为(其中,为常数). 示例:如图2,格点多边形内的格点数,边界上的格点数,格点多边形的面积. 图2
问题解决
任务1 在图3中画一个格点多边形,并计算它的格点多边形内的格点数,边界上的格点数和面积. ; ; . 图3
任务2 得出格点多边形的面积公式 根据图2和图3的数据,求常数,的值.
任务3 计算油漆的用量 求需要红色油漆多少升?
9.根据以下素材,完成探索任务.
探索果园土地规划和销售利润问题
素材1 某农户承包了一块长方形果园,图1是果园的平面图,其中米,米.准备在它的四周铺设道路,上下两条横向道路的宽度都为米,左右两条纵向道路的宽度都为米,中间部分种植水果.已知道路的路面造价是50元;出于货车通行等因素的考虑,道路宽度不超过12米,且不小于5米.
素材2 该农户发现某一种草莓销售前景比较不错,经市场调查,草莓培育一年可产果,已知每平方米的草莓销售平均利润为100元;果园每年的承包费为25万元,期间需一次性投入33万元购进新苗,每年还需25万元的养护、施肥、运输等其余费用.
问题解决
任务1 解决果园中路面宽度的设计对种植面积的影响. (1)请直接写出纵向道路宽度的取值范围. (2)若中间种植的面积是,则路面设置的宽度是否符合要求.
任务2 解决果园种植的预期利润问题.(净利润草莓销售的总利润路面造价费用果园承包费用新苗购置费用其余费用) (3)经过1年后,农户是否可以达到预期净利润400万元?请说明理由.
10.根据以下素材,探索完成任务.
如何估算游客人数和门票收入?
素材1 今年疫情开放以来,我县接待的游客人数逐月增加,据统计,游玩某景区的游客人数1月份为4万人,3月份为5.76万人.
素材2 若该景区仅有,两个景点,售票处出示的三种购票方式如表所示: 据预测,5月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万.并且当甲、乙两种门票价格不变时,丙种门票价格每下降1元,将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票. 购票方式 甲 乙 丙
可游玩景点 和
门票价格 100元人 80元人 160元人
问题解决
任务1 确定增长率 求2月和3月这两个月中,该景区游客人数平均每月增长百分之几.
任务2 预计门票收入 若丙种门票价格下降10元,求景区5月份的门票总收入.
任务3 拟定价格方案 将丙种门票价格下降多少元时,景区5月份的门票总收入有816万元?
11.综合实践:
项目主题 “亚运主题”草坪设计
项目情境 为了迎亚会,同学们参与一块长为40米,宽为30米的矩形“亚运主题”草 坪方案设计的项目学习.以下为项目学习小组对草坪设计的研究过程.
活动任务一 请设计两条相同宽度的小路连接矩形草坪两组对边.小组内同学们设计的方案主要有甲、乙、丙、丁四种典型的方案
驱动问题一 (1)项目小组设计出来的四种方案小路面积的大小关系? ①直观猜想:我认为 ; 请用简洁的语言或代数式表达你的猜想) ②具体验证:选择最简单的甲、乙方案,假设小路宽为1米,则甲、乙方案中小路的面积分别为 和 ; ③一般验证:若小路宽为米,则甲、乙方案中小路所占的面积分别为 和 .
活动任务二 为施工方便,学校选择甲种方案设计,并要求除小路后草坪面积约为1064平方米.
驱动问题二 (2)请计算两条小路的宽度是多少?
活动任务三 为了布置五环标志等亚运元素,将在草坪上的亚运宣传主题墙前,用篱笆围(三边) 成面积为100平方米的矩形,如图.
驱动问题三 (3)为了使篱笆恰好用完同时围住三面,项目小组的同学对下列问题展开探究,其中矩形宽,长. ①若30米长的篱笆,请用两种不同的函数表示关于的函数关系. ②数学之星小明提出一个问题:若米长的篱笆恰好用完,且有两种不同方案可以选择,使得两种方案的宽之和小于15米,甲同学说“篱笆的长可以是28米”,乙同学说“篱笆的长可以是32米”,你认为他们俩的说法对吗?请说明理由.
【初二下专题4】项目化学习(PBL)类问题
参考答案与试题解析
1.(1)解:储物区域的长为,由于收纳盒可以完全放入储物区域,
则图1中的四角裁去小正方形的边长为,
则收纳盒的宽小正方形的边长,
由图2知,设小正方形的边长为,
由题意可得:,
解得:,
体积为,
答:储物盒的容积为6552立方厘米;
(2)设小长方形的宽为,,长为,
由题意可得:,
解得:
小长方形的宽为
当,之间两边恰好重合且无重叠部分,收纳盒的高为,
玩具机械狗也不能完全放入该储物;
综上所述:玩具机械狗不能完全放入该储物.
答:玩具机械狗不能完全放入该储物.
2.(1)解:由正方形的对角线的性质,边长为,对角线的一半为;
圆柱体的底面半径为,所以它的高.
(2)解裁剪掉的废料部分的面积与原图形的面积之比称为材料的损耗率,
裁剪掉的废料部分的面积,原图形的面积,
所以列方程为:.
解得.
由,得.
得.
答:这个圆柱体的底面半径为1.2.
(3)设两个圆柱的底面半径分别为和,则有,
得,
由题意,得
解得,(不合题意,舍去),
答:第一个圆柱体的底面半径为.
3.解:任务1:依题意,镇流器补进90件,学校补进镇流器和灯管共元,
答:若镇流器补进90件,则学校补进镇流器和灯管共15600元,
任务2:设镇流器补进件,若,刚补进镇流器的单价为(元,
补进灯管的总价为:(元,
故答案为:;.
任务3:依题意,,
解得:,,
.
.
当时,
依题意,,
解得:,
当时,镇流器的单价固定为50元,
,
.
答:补进镇流器100件或60件或150件.
4.解:任务一:设每平方米增加株作物为正整数),则每平方米有株,单株产量为千克,
故答案为:,;
任务二:根据题意得:,
整理得:,
解得:,,
或,
答:每平方米应种植6株或8株;
任务三:设种植作物每平方米的产量为千克,
根据题意得:,
,
当时,有最大值,最大值为4.9,
种植作物每平方米最大产量为1.9千克,
根据题意得:,
解得,
则的取值范围是,
故答案为:.
5.解:任务
问题
点是的黄金分割点,理由如下:
由旋转可得:,,,
为的黄金分割点,
,
,
点是上的黄金分割点;
问题
直线不是四边形的黄金分割线,
故答案为:直线不是四边形的黄金分割线;
任务
边上存在点,使得直线是四边形的黄金分割线,
过点作交于点,则是四边形的黄金分割线,
如图:
点即为所求的点;
任务
正确,理由如下:
如图:
是的黄金分割点,
,
,,
,
是三角形的黄金分割线;
任务
证明:连接,如图:
,
,,
,,
点是的边的黄金分割点,
,
,
,
直线是的黄金分割线.
6.解:任务1.由题意得:,
,
.
设,则,
矩形的面积为三角形面积的,
,
化简得,
解得:或,
矩形的边长为,,
周长为;
任务2.由题意得:,,
,,
.
设,则,
矩形的面积为三角形面积的,
,
整理得:.
△,
方程无实数根,
乙同学的方案不能实现;
任务3.图2方案:,
当时,矩形的面积最大为;
图3方案:,
当 时,面积最大为,
长方形纸片面积的最大值为.
7.解:任务1,甲店每天的销售量为件,乙店每天的销售量为件,
故答案为:件,件;
任务2,当时,甲店每天的盈利为(元;
当时,乙店每天的盈利为(元;
任务3,设每件衬衫下降元时,两家分店一天的盈利和为2244元,
由题意得:,
整理得:,
解得:,
即每件衬衫下降11元时,两家分店一天的盈利和为2244元.
8.
解:任务一:如图,即为所求.
观察图象可知:,,,
故答案为:1,8,4;
任务二:由题意,,
解得,
;
任务三:由题意,,,
,
(升.
9.解:(1)道路宽度不超过12米,且不小于5米,
纵向道路宽度的取值范围为;
(2)根据题意得:,
整理得:,
解得:,,
,
符合题意,
路面设置的宽度符合要求;
(3)经过1年后,农户可以达到预期净利润400万元,理由如下:
假设经过1年后,农户可以达到预期净利润400万元,
根据题意得:,
整理得:,
解得:,,
又,
符合题意,
假设成立,
即经过1年后,农户可以达到预期净利润400万元.
10.解:(任务设2月和3月这两个月中,该景区游客人数平均每月增长率为,
根据题意得:,
解得:,(不符合题意,舍去).
答:2月和3月这两个月中,该景区游客人数平均每月增长;
(任务根据题意得:
(元,
7980000元万元.
答:景区5月份的门票总收入798万元;
(任务设丙种门票价格下降元时,景区5月份的门票总收入有816万元,
根据题意得:,
整理得:,
解得:,.
答:丙种门票价格下降20元或28元时,景区5月份的门票总收入有816万元.
【点评】本题考查了一元二次方程的应用以及有理数的混合运算,找准等量关系,正确列出一元二次方程是解题的关键.
11.解:(1)①直观猜想:我认为:四种方案小路面积的大小相等,
故答案为:四种方案小路面积的大小相等;
②甲:;
乙:,
故答案为:,;
③甲:,
乙:,
故答案为:,;
(2)设小路的宽为,则,
解得:或(不合题意,舍去),
答:小路的宽为;
(3)①方法,,
方法,;
②由题意得:,
设方程的两个根分别为,,则,且△,
则:,,
,
,
故甲和乙的说法都不正确.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
