浙江省宁波市宁海县长街镇初级中学浙教版七年级上册数学课件:3.2实数(共23张PPT)
文档属性
| 名称 | 浙江省宁波市宁海县长街镇初级中学浙教版七年级上册数学课件:3.2实数(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 363.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-12 14:20:07 | ||
图片预览








文档简介
课件23张PPT。3.2 实 数
(1) 16的平方根是4
(2) 16的算术平方根是4
(3) -4是16的平方根
(4) 16的平方根是4与-4判断题
(5)平方根等于本身的数1,0
(6)算术平方根等于本身的数是1
(7)-1的平方根是+1与-1
判断题
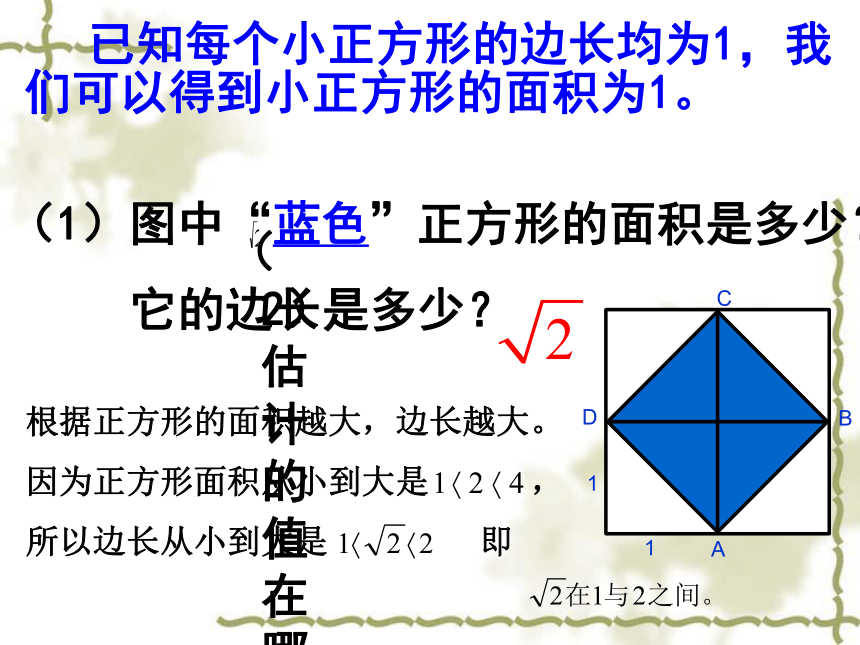
2的算术平方根记作填空题“海神错判” 约公元600年,毕达哥拉斯学派认为宇宙万物的总规律是服从整数化,认为世界上一切现象,都能归结为整数或整数之比。正当毕氏学派津津乐道地高唱“万物皆数”时,该学派的一位成员希伯索斯利用推理的方法发现,边长为1的正方形的对角线长既不是整数,也不是整数的比(分数)所能表示的.“海神错判” 这个发现被人们看成是“荒谬”和违反常识的事。对于只有整数和整数比概念的他们来说,这意味着边长为1的正方形的对角线长竟然不能用任何“数”来表示!这在数学史上称为第一次数学危机。最后希伯索斯的发现没有被毕达哥拉斯学派的信徒所接受,相传就因为这一发现,毕达哥拉斯学派把希伯索斯投入大海中处死。 已知每个小正方形的边长均为1,我们可以得到小正方形的面积为1。(1)图中“蓝色”正方形的面积是多少?
它的边长是多少?CDBA11<<<<<<<<<<<<<<<<<<<<…………像 这种无限不循环小数叫做无理数(irrational number). 无理数广泛存在着,一般有三种情况:
例如:带根号的数都是无理数,这种说法对吗?第二种: 有一定的规律,但不循环的无限小数都是无理数。例如:
0.1010010001…〔两个1之间依次多1个0〕
234.232232223…〔两个3之间依次多1个2〕0.12345678910111213 …〔小数部分有相继的正整数组成〕
第三种:实数有理数正有理数负有理数零无理数正无理数负无理数有理数和无理数统称为实数。或有理数整数分数(无限不循环小数)课内练习在 中属于有理数的有:__________________;属于无理数的有:________________;属于实数的有:______________________.把数从有理数扩充到实数以后,有理数的相反数和绝对值的概念同样适用于实数。和 互为相反数例如:绝对值等于 的数是做一做: 填空:
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值不大于 的 整数是 -1,0,10-1121AB 如图:OA=OB,数轴上A点对应的数是什么? 如果将所有有理数都标到数轴上,那么数轴被填满了吗?探索 & 交流在实数范围内,每一个数都可以用数轴上的点来表示;反过来,数轴上的每一个点都表示一个实数。实数与数轴上的点一一对应。 把下列实数表示在数轴上,并比较它们的大小(用“<”号连接)-1.43.31.5例题一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.两个无理数之积不一定是无理数。( )7.两个无理数之和一定是无理数。( )8.数轴上的任何一点都可以表示实数。( )×××
(1)1.7 和
例:比较下列各组里两个数的大小.(2)(1)无理数、实数的概念,实数的分类;
(2)知道实数与数轴上的点一一对应,能将实数表示在数轴上;
(3)相反数、绝对值、数的大小比较法则同样适用于实数.小结
(1) 16的平方根是4
(2) 16的算术平方根是4
(3) -4是16的平方根
(4) 16的平方根是4与-4判断题
(5)平方根等于本身的数1,0
(6)算术平方根等于本身的数是1
(7)-1的平方根是+1与-1
判断题
2的算术平方根记作填空题“海神错判” 约公元600年,毕达哥拉斯学派认为宇宙万物的总规律是服从整数化,认为世界上一切现象,都能归结为整数或整数之比。正当毕氏学派津津乐道地高唱“万物皆数”时,该学派的一位成员希伯索斯利用推理的方法发现,边长为1的正方形的对角线长既不是整数,也不是整数的比(分数)所能表示的.“海神错判” 这个发现被人们看成是“荒谬”和违反常识的事。对于只有整数和整数比概念的他们来说,这意味着边长为1的正方形的对角线长竟然不能用任何“数”来表示!这在数学史上称为第一次数学危机。最后希伯索斯的发现没有被毕达哥拉斯学派的信徒所接受,相传就因为这一发现,毕达哥拉斯学派把希伯索斯投入大海中处死。 已知每个小正方形的边长均为1,我们可以得到小正方形的面积为1。(1)图中“蓝色”正方形的面积是多少?
它的边长是多少?CDBA11<<<<<<<<<<<<<<<<<<<<…………像 这种无限不循环小数叫做无理数(irrational number). 无理数广泛存在着,一般有三种情况:
例如:带根号的数都是无理数,这种说法对吗?第二种: 有一定的规律,但不循环的无限小数都是无理数。例如:
0.1010010001…〔两个1之间依次多1个0〕
234.232232223…〔两个3之间依次多1个2〕0.12345678910111213 …〔小数部分有相继的正整数组成〕
第三种:实数有理数正有理数负有理数零无理数正无理数负无理数有理数和无理数统称为实数。或有理数整数分数(无限不循环小数)课内练习在 中属于有理数的有:__________________;属于无理数的有:________________;属于实数的有:______________________.把数从有理数扩充到实数以后,有理数的相反数和绝对值的概念同样适用于实数。和 互为相反数例如:绝对值等于 的数是做一做: 填空:
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值不大于 的 整数是 -1,0,10-1121AB 如图:OA=OB,数轴上A点对应的数是什么? 如果将所有有理数都标到数轴上,那么数轴被填满了吗?探索 & 交流在实数范围内,每一个数都可以用数轴上的点来表示;反过来,数轴上的每一个点都表示一个实数。实数与数轴上的点一一对应。 把下列实数表示在数轴上,并比较它们的大小(用“<”号连接)-1.43.31.5例题一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.两个无理数之积不一定是无理数。( )7.两个无理数之和一定是无理数。( )8.数轴上的任何一点都可以表示实数。( )×××
(1)1.7 和
例:比较下列各组里两个数的大小.(2)(1)无理数、实数的概念,实数的分类;
(2)知道实数与数轴上的点一一对应,能将实数表示在数轴上;
(3)相反数、绝对值、数的大小比较法则同样适用于实数.小结
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
