浙教版九年级上册数学第一章二次函数(含解析)
文档属性
| 名称 | 浙教版九年级上册数学第一章二次函数(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 321.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 22:27:12 | ||
图片预览




文档简介
浙教版九年级上册数学第一章二次函数
一、选择题
1.下列各式中,y是x的二次函数的是( )
A. B. C. D.
2.抛物线的顶点坐标是( )
A.(1,﹣2) B.(﹣1,2)
C.(1,2) D.(﹣1,﹣2)
3.抛物线向右平移2个单位,再向下平移3个单位,得到新的抛物线解析式是( )
A. B.
C. D.
4.抛物线 与 轴的交点坐标是( )
A. B. C. D.
5.用配方法将二次函数化为的形式为( ).
A. B.
C. D.
6.抛物线与x轴的公共点个数是( )
A.0个 B.1个 C.2个 D.3个
7.已知,,三点都在抛物线上,则、、的大小关系为( )
A. B. C. D.
8.九年级某学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为y=,由此可知该生此次实心球训练的成绩为( )
A.6米 B.10米 C.12米 D.15米
9.已知二次函数的对称轴为,当时,y的取值范围是.则的值为( )
A.或 B.或 C. D.
10.如图,二次函数及一次函数,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数,当直线与新图象有4个交点时,m的取值范围是( )
A. B. C. D.
二、填空题
11.二次函数 的最大值是 .
12.若抛物线y=x2﹣6x+c的顶点在x轴,则c= .
13.如图,抛物线y=ax2+c与直线y=kx+m交于A(﹣3,y1)、B(1,y2)两点,则关于x的不等式ax2+c≥﹣kx+m的解集是 .
14.如图,在平面直角坐标系中,抛物线交x轴正半轴于点C,交y轴于点A,轴交抛物线于点B,则△ABC的面积是 .
15.如图,同学们在操场上玩跳大绳游戏,绳甩到最高处时的形状是抛物线型,摇绳的甲、乙两名同学拿绳的手的间距为米,到地面的距离与均为米,绳子甩到最高点处时,最高点距地面的垂直距离为米身高为米的小吉站在距点水平距离为米处,若他能够正常跳大绳绳子甩到最高时超过他的头顶,则的取值范围是 .
16.如图,已知抛物线.
⑴抛物线与y轴的交点B的坐标为 ;
⑵P是抛物线在第四象限上的一点,过点P分别向x轴和y轴作垂线,垂足分别为点A、C,则四边形周长的最大值为 .
三、解答题
17.已知二次函数的图象的顶点坐标为(﹣2,﹣3),且图象过点(﹣3,﹣2),求这个二次函数的解析式.
18.请在如图坐标系中直接描点,画出函数的图象,并回答下列问题:
(1)抛物线的开口方向为 ;
(2)抛物线的对称轴是直线 ;
(3)若将抛物线的图象向上平移1个单位,再向右平移2个单位,则解析式为 .
19.已知二次函数的图象经过点.
(1)求的值;
(2)判断是否在该函数的图象上,并说明理由.
20.已知抛物线与轴交于点,当时,随的增大而减小,当时,随的增大而增大.
(1)求的值;
(2)若点(其中)在抛物线上,求的值.
21.小明对他击羽毛球的路线进行分析.如图,在平面直角坐标系中,点A,C在x轴上,球网与y轴的水平距离,,击球点P在y轴上.若小明选择扣球,羽毛球的飞行高度与水平距离近似满足一次函数关系;若小明选择吊球,羽毛球的飞行高度与水平距离近似满足二次函数关系.
(1)求点P的坐标和a的值;
(2)通过分析发现,上面两种击球方式均能使球过球网.要使球的落地点到点C的距离更近,请通过计算判断应选择哪种击球方式;
(3)小明在点P处再次以吊球的方式击球,此次羽毛球飞行路线的形状与的相同,且恰好落到点C处,则此次羽毛球飞行到最高点时与y轴的水平距离比 (填“大”或“小”).
22.在平面直角坐标系xOy中,等腰直角△ABC的直角顶点C在y轴上,另两个顶点A,B在x轴上,AB=4,抛物线经过A,B,C三点,如图1所示.
(1)求抛物线所表示的二次函数表达式.
(2)过原点任作直线l交抛物线于M,N两点,如图2所示.
①求△CMN面积的最小值.
②已知物线上一定点,问抛物线上是否存在点P,使得点P与点Q关于直线l对称,若存在,请直接写出点P的坐标及直线l的解析式;若不存在,请说明理由.
23.如图1,在平面直角坐标系中,O为坐标原点,抛物线与x轴负半轴交于点B,与x轴正半轴于点,交y轴于点C,连接,.
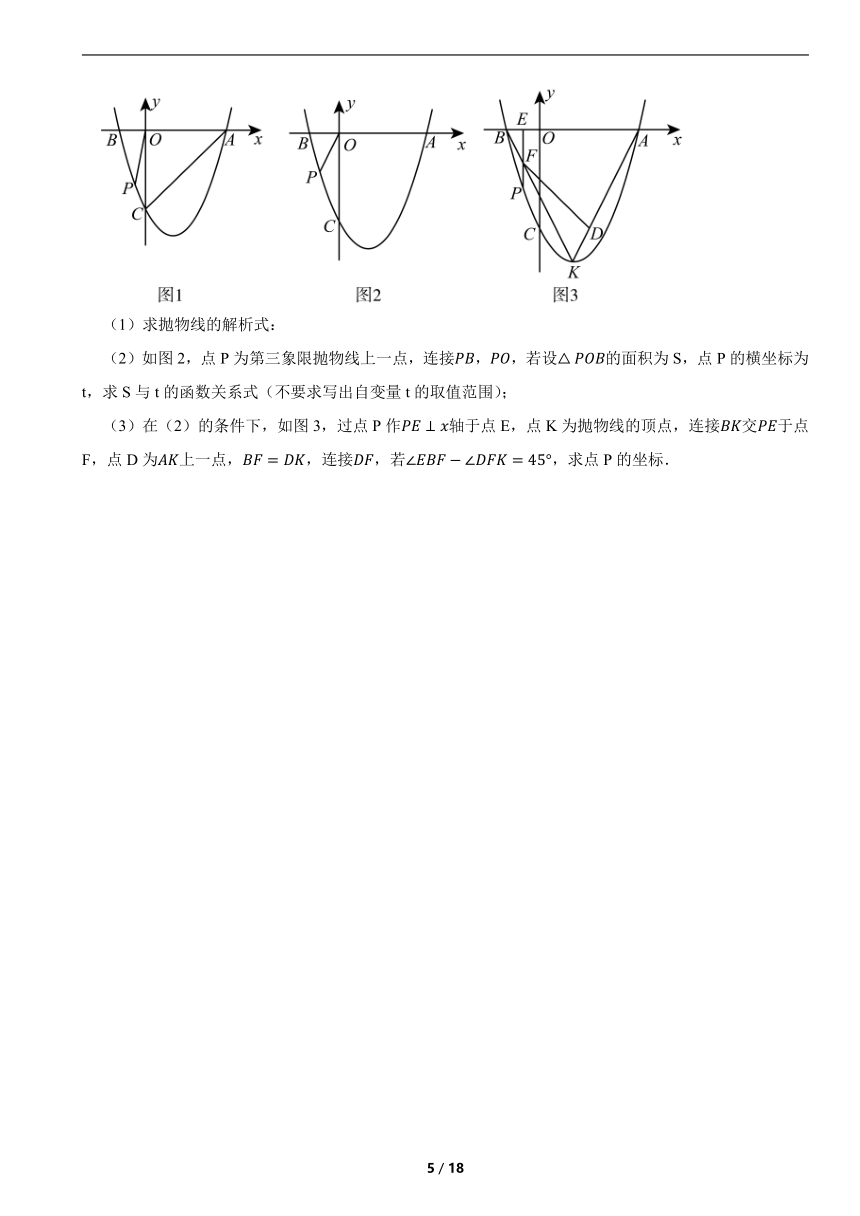
(1)求抛物线的解析式:
(2)如图2,点P为第三象限抛物线上一点,连接,,若设的面积为S,点P的横坐标为t,求S与t的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,如图3,过点P作轴于点E,点K为抛物线的顶点,连接交于点F,点D为上一点,,连接,若,求点P的坐标.
答案解析部分
1.【答案】C
【解析】【解答】解A、此函数不是二次函数,故A不符合题意;
B、此函数不是二次函数,故B不符合题意;
C、此函数是二次函数,故C符合题意;
D、此函数不是二次函数,故D不符合题意;
故答案为:C.
【分析】根据二次函数的定义:形如y=ax2+bx+c=0(a,b,c是常数且a≠0)则y是x的二次函数,再对各选项逐一判断.
2.【答案】D
【解析】【解答】解:∵抛物线的解析式为,
∴抛物线的顶点坐标为(-1,-2),
故答案为:D.
【分析】利用抛物线的顶点式直接求出顶点坐标即可.
3.【答案】B
【解析】【解答】解: 抛物线向右平移2个单位,再向下平移3个单位后的解析式为 .
故答案为:B.
【分析】 抛物线平移规律:左加右减,上加下减,据此解答即可.
4.【答案】A
【解析】【解答】解:令 ,
则
=
∴抛物线 与 轴的交点坐标是(0,-3),
故答案为:A.
【分析】由题意令x=0可得y的值,则抛物线与y轴的交点坐标可求解.
5.【答案】B
【解析】【解答】解:y=x2-8x+16-16-9=(x-4)2-25.
故答案为:B.
【分析】利用配方法将函数解析式转化为y=a(x-h)2+k的形式.
6.【答案】B
【解析】【解答】将y=0代入可得,
∵△=b2-4ac=42-4×(-1)×(-4)=16-16=0,
∴一元二次方程有两个相等的实数根,
∴抛物线与x轴的公共点个数是1个,
故答案为:B.
【分析】将二次函数与x轴的交点个数的问题转换为一元二次方程根的判别式分析求解即可.
7.【答案】B
【解析】【解答】解:
对称轴为.
a=1>0,抛物线开口向上,
所以点到对称轴距离越远,对应的函数值越大.
∵A到对称轴距离:;B到对称轴距离:;C到对称轴距离:;
∴.
故答案为:B.
【分析】求出抛物线的对称轴,根据点到对称轴的距离以及抛物线的开口方向即可判断函数值的大小.
8.【答案】B
【解析】【解答】解:∵ 实心球飞行高度y(米)与水平距离x(米)之间的关系为,铅球落地点y=0,
∴
解得:x=-2(舍去),x=10,
则该生此次实心球训练的成绩为10米.
故答案为:B.
【分析】根据解析式和铅球的落地点y=0,可得,据此求出x的值再选择.
9.【答案】D
【解析】【解答】∵二次函数的对称轴为,
∴b=1,
∴,
∴当x=1时,y有最大值,
①当时,y的最大值为2n,即x=1时,2n=,解得:n=;
当x=m时,y有最小值为2m,即,解得:m1=-2,m2=0(舍),
∴m+n=-2+;
②当时,y的最大值为2m,即x=1时,2m=,解得:m=;
当x=n时,y有最小值为2m,即,解得:n1=2,n2=-1(舍),
∴m+n=2+;
综上,的值为或.
【分析】分类讨论:①当时,y的最大值为2n,②当时,y的最大值为2m,再分别求出m、n的值,最后求出的值即可.
10.【答案】D
【解析】【解答】解:在中,
当,,
解得,,
,,
当时,,
∴原抛物线与轴交点坐标为,
∴翻折后与y轴的交点坐标为,
当直线经过点B时,直线与新图有3个交点,如图所示:
把代入中,得,
∵抛物线翻折到x轴下方的部分的解析式为:,
∴翻折后的部分解析式为:,
当直线与抛物线只有一个交点C时,
直线与图象有3个交点,
把代入中,
得到方程有两个相等的实数根,
整理得,
∴,
解得,
∴当直线与新图象有4个交点时,m的取值范围是.
故答案为:D.
【分析】令,代入可得,,如图,过点B作直线,代入可得,将直线往下平移,当直线与翻折后抛物线部分解析式只有一个交点C时,直线与图象有3个交点,结合图像可得,根据判别式即可求得,观察图像,可知一次函数在这两条直线间与新图象有4个交点,据此即可求解。
11.【答案】8
【解析】【解答】∵ ,
∴ 有最大值,
当 时, 有最大值8.
故答案为8.
【分析】二次函数的顶点式 在x=h时有最值,a>0时有最小值,a<0时有最大值,题中函数 ,故其在 时有最大值.
12.【答案】9
【解析】【解答】解:根据题意,顶点在x轴上,顶点纵坐标为0,
即
解得:c=9,
故答案为:9.
【分析】根据顶点在x轴上,可得顶点的纵坐标是0,结合顶点坐标公式,代入求解即可.
13.【答案】﹣1≤x≤3
【解析】【解答】解:∵y=kx+m与y=-kx+m的图象关于y轴对称
∴直线y=-kx+m与抛物线 y=ax2+c的交点A‘,B’与点A、B也关于y轴对称,
如图所示:
∵A(﹣3,y1)、B(1,y2)
∴A'( 3, y1 ),B'(-1,y2),
根据函数图象得:不等式 ax2+c≥﹣kx+m 的解集是 ﹣1≤x≤3 .
故答案为: ﹣1≤x≤3.
【分析】y=kx+m与y=-kx+m的图象关于y轴对称,利用数形结合思想,把不等式的解集转化为图象的交点问题求解。
14.【答案】2
【解析】【解答】解:当时,,
∴,
抛物线的对称轴为,
又轴交抛物线于点B,
∴,
∴的面积是.
故答案为:2.
【分析】先求出点A的坐标和抛物线的对称轴,再根据抛物线的对称性求出点B的坐标,最后根据三角形的面积公式求解即可.
15.【答案】
【解析】【解答】解:如图,
由题意可知C(3,1.8),
设抛物线的解析式为y=a(x﹣3)2+1.8,
把A(0,0.9)代入y=a(x﹣3)2+1.8,得
a=﹣0.1,
∴所求的抛物线的解析式是y=﹣0.1(x﹣3)2+1.8,
当y=1.4时,﹣0.1(x﹣3)2+1.8=1.4,
解得x1=1,x2=5,
∴则m的取值范围是1<m<5.
故答案为:1<m<5.
【分析】先确定顶点C的坐标,设二次函数的解析式为顶点式,再把A(0,0.9)代入求出a=﹣0.1,写出解析式求解即可。
16.【答案】;
【解析】【解答】解:(1),
当时,,
∴.
故答案为:
(2)设,则,
∴令四边形周长为,,
∵,
∴时,取最大值,为.
故答案为:
【分析】(1)令x=0,即可求得抛物线与y轴的交点B的坐标;
(2)设,则,可得四边形周长,根据函数的最大值,求得 则四边形周长的最大值为。
17.【答案】解:设解析式为:y=a(x+2)2﹣3,
将(﹣3,﹣2)代入得出:﹣2=a(﹣3+2)2﹣3,
解得:a=1.
故这个二次函数的解析式为:y=(x+2)2﹣3.
【解析】【分析】利用待定系数法求出二次函数解析式即可.
18.【答案】(1)向下
(2)x=﹣1
(3)
【解析】【解题】 应改为 , 列表如下:
描点、连线如下图,
【分析】(1)根据列表、描点、连线画出函数图象,即可求解;
(2)根据函数图象即可求解;
(3)根据函数图象的几何变换“上加下减、左加右减”即可求解.
19.【答案】(1)解:∵ 的图象经过,代入得
,
.
(2)解:当时,
∴P(2,3)是在这个二次函数的图象上.
【解析】【分析】(1)把点A坐标带入二次函数的解析式即可求出b的值;
(2)把x=2代入二次函数的解析式,若y值等于3,则说明在函数图象上,否则就不在.
20.【答案】(1)解:抛物线与轴交于点,∴
∵当时,随的增大而减小,当时,随的增大而增大,
∴抛物线对称轴为:,∴,解得:.
(2)解:由(1)知,抛物线的解析式为:.
∵点在抛物线上,∴.
原式,将代入可得,
原式
,
∴的值为.
21.【答案】(1)解:在一次函数,
令时,,
∴,
将代入中,可得:,
解得:;
(2)解:∵,,
∴,
选择扣球,则令,即:,解得:,
即:落地点距离点距离为,
∴落地点到C点的距离为,
选择吊球,则令,即:,
解得:(不合题意,舍去),
即:落地点距离点距离为,
∴落地点到C点的距离为,
∵,
∴选择吊球,使球的落地点到C点的距离更近.
(3)大
【解析】【解答】(3)解:∵,,
∴,
∴点C的坐标为,
设抛物线的解析式为,把点P和点C的坐标代入得到,
解得,
即此时抛物线的解析式为,
∴此次飞行路线的最高点是,
∴此次羽毛球飞行到最高点时与y轴的水平距离为,
即此次羽毛球飞行到最高点时与y轴的水平距离比大.
故答案为:大
【分析】(1)对于一次函数,令x=0,可求得点P的坐标,再代入二次函数即可求得的值;
(2)由题意可知OC=5,令y=0,代入两个函数的解析式,建立方程,即可求得落地点到O点的距离,即可判断谁更近;
(3)用待定系数法求出此时抛物线的解析式,确定此次飞行路线的最高点的坐标,即可得到答案.
22.【答案】(1)解:设抛物线的解析式为y=ax2+bx+c(a≠0),
在等腰Rt△ABC中,OC垂直平分AB,且AB=4,
∴OA=OB=OC=2,
∴A(﹣2,0),B(2,0),C(0,﹣2),代入解析式得:
,
解得,,
∴抛物线的解析式为y=﹣2;
(2)解:①设直线l的解析式为y=kx,M(x1,y1),N(x2,y2),
由 , 可得
∴x1+x2=2k,x1 x2=﹣4,
∴,
∴,
∴,
∴当k=0时2取最小值为4.
∴△CMN面积的最小值为4.
②存在,点P(,﹣),直线l的解析式为y=(1﹣)x或点P(﹣,﹣),直线l的解析式为y=(1+)x.
【解析】【解题】(2) ② 设抛物线上存在点P(a,), 使得点P与点Q关于直线l对称,
可得PO=PQ,
解得:
(不合题意,舍去),
当时,点
线段PQ的中点为
直线l的表达式为:
当时,点
线段PQ的中点为
直线l的表达式为:
综上所述:点直线l的表达式或.
【分析】(1) 设抛物线的解析式为y=ax2+bx+c(a≠0), 由等腰直角三角形的性质以及AB的值求得 OA=OB=OC=2, 从而得到A、B、C三点的坐标,利用待定系数法求得a、b、c的值,即可求解;
(2) ①设直线l的解析式为y=kx,M(x1,y1),N(x2,y2), 联立方程组得到 ,利用根与系数的关系得到 , 再由三角形的面积公式得到 ,从而求解;②设抛物线上存在点P(a,), 使得点P与点Q关于直线l对称,可得PO=PQ,列出关于m的方程,解得PQ的中点坐标,即可求解.
23.【答案】(1)解:∵抛物线与轴正半轴于点,
∴,
∵在中, ,
∴,
∴
把点、代入得:
解得
∴抛物线的解析式为;
(2)解:当时,
解得:,
∴,
∴,
∵点P在抛物线上,点P的横坐标为,
∴,
过点P作轴于点L,
∴,
∴;
(3)解:∵,
∴,
过点K作于点M,交于点N,作于点G,
根据对称性可知:,, ,
∵,
∴,
∴,
设,
∴,
∵,
∴,
∴
,
∴,
∴,
过点D作,
∵,,,
∴,
∴,,
过点F作于T,
∵,
∴与都是等腰直角三角形,
∴,,,
∵,,
∴
∵点P的横坐标为t,
∴,
∴,
∴,
∴,
解得:,
,
∴.
【解析】【分析】(1)根据已知的锐角三角函数可求出点C的坐标,然后用待定系数法可求解;
(2)令解析式中的y=0可得关于x的一元二次方程,解方程可求出点B的坐标,过点P作Pl⊥x轴于点L,用含t的代数式将PL表示出来,然后根据三角形的面积公式即可求解;
(3)由题意将所求出的二次函数的解析式配成顶点式可得顶点K的坐标,过点K作KM⊥AB于点M,交DF于点N,作FG⊥AK于点G,结合轴对称的性质可证△DHK≌△BEF,则可得DH=BE,HK=EF,过点F作FT⊥KM于T,易证△FTN和△HND是等腰直角三角形,于是可得DH=HN,FT=EM=TN,EF=MT=HK,根据线段的构成Mk=HK+HN+TN+MT可得关于t的方程,解方程即可求出t的值,于是点P的坐标可求解..
1 / 1
一、选择题
1.下列各式中,y是x的二次函数的是( )
A. B. C. D.
2.抛物线的顶点坐标是( )
A.(1,﹣2) B.(﹣1,2)
C.(1,2) D.(﹣1,﹣2)
3.抛物线向右平移2个单位,再向下平移3个单位,得到新的抛物线解析式是( )
A. B.
C. D.
4.抛物线 与 轴的交点坐标是( )
A. B. C. D.
5.用配方法将二次函数化为的形式为( ).
A. B.
C. D.
6.抛物线与x轴的公共点个数是( )
A.0个 B.1个 C.2个 D.3个
7.已知,,三点都在抛物线上,则、、的大小关系为( )
A. B. C. D.
8.九年级某学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为y=,由此可知该生此次实心球训练的成绩为( )
A.6米 B.10米 C.12米 D.15米
9.已知二次函数的对称轴为,当时,y的取值范围是.则的值为( )
A.或 B.或 C. D.
10.如图,二次函数及一次函数,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数,当直线与新图象有4个交点时,m的取值范围是( )
A. B. C. D.
二、填空题
11.二次函数 的最大值是 .
12.若抛物线y=x2﹣6x+c的顶点在x轴,则c= .
13.如图,抛物线y=ax2+c与直线y=kx+m交于A(﹣3,y1)、B(1,y2)两点,则关于x的不等式ax2+c≥﹣kx+m的解集是 .
14.如图,在平面直角坐标系中,抛物线交x轴正半轴于点C,交y轴于点A,轴交抛物线于点B,则△ABC的面积是 .
15.如图,同学们在操场上玩跳大绳游戏,绳甩到最高处时的形状是抛物线型,摇绳的甲、乙两名同学拿绳的手的间距为米,到地面的距离与均为米,绳子甩到最高点处时,最高点距地面的垂直距离为米身高为米的小吉站在距点水平距离为米处,若他能够正常跳大绳绳子甩到最高时超过他的头顶,则的取值范围是 .
16.如图,已知抛物线.
⑴抛物线与y轴的交点B的坐标为 ;
⑵P是抛物线在第四象限上的一点,过点P分别向x轴和y轴作垂线,垂足分别为点A、C,则四边形周长的最大值为 .
三、解答题
17.已知二次函数的图象的顶点坐标为(﹣2,﹣3),且图象过点(﹣3,﹣2),求这个二次函数的解析式.
18.请在如图坐标系中直接描点,画出函数的图象,并回答下列问题:
(1)抛物线的开口方向为 ;
(2)抛物线的对称轴是直线 ;
(3)若将抛物线的图象向上平移1个单位,再向右平移2个单位,则解析式为 .
19.已知二次函数的图象经过点.
(1)求的值;
(2)判断是否在该函数的图象上,并说明理由.
20.已知抛物线与轴交于点,当时,随的增大而减小,当时,随的增大而增大.
(1)求的值;
(2)若点(其中)在抛物线上,求的值.
21.小明对他击羽毛球的路线进行分析.如图,在平面直角坐标系中,点A,C在x轴上,球网与y轴的水平距离,,击球点P在y轴上.若小明选择扣球,羽毛球的飞行高度与水平距离近似满足一次函数关系;若小明选择吊球,羽毛球的飞行高度与水平距离近似满足二次函数关系.
(1)求点P的坐标和a的值;
(2)通过分析发现,上面两种击球方式均能使球过球网.要使球的落地点到点C的距离更近,请通过计算判断应选择哪种击球方式;
(3)小明在点P处再次以吊球的方式击球,此次羽毛球飞行路线的形状与的相同,且恰好落到点C处,则此次羽毛球飞行到最高点时与y轴的水平距离比 (填“大”或“小”).
22.在平面直角坐标系xOy中,等腰直角△ABC的直角顶点C在y轴上,另两个顶点A,B在x轴上,AB=4,抛物线经过A,B,C三点,如图1所示.
(1)求抛物线所表示的二次函数表达式.
(2)过原点任作直线l交抛物线于M,N两点,如图2所示.
①求△CMN面积的最小值.
②已知物线上一定点,问抛物线上是否存在点P,使得点P与点Q关于直线l对称,若存在,请直接写出点P的坐标及直线l的解析式;若不存在,请说明理由.
23.如图1,在平面直角坐标系中,O为坐标原点,抛物线与x轴负半轴交于点B,与x轴正半轴于点,交y轴于点C,连接,.
(1)求抛物线的解析式:
(2)如图2,点P为第三象限抛物线上一点,连接,,若设的面积为S,点P的横坐标为t,求S与t的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,如图3,过点P作轴于点E,点K为抛物线的顶点,连接交于点F,点D为上一点,,连接,若,求点P的坐标.
答案解析部分
1.【答案】C
【解析】【解答】解A、此函数不是二次函数,故A不符合题意;
B、此函数不是二次函数,故B不符合题意;
C、此函数是二次函数,故C符合题意;
D、此函数不是二次函数,故D不符合题意;
故答案为:C.
【分析】根据二次函数的定义:形如y=ax2+bx+c=0(a,b,c是常数且a≠0)则y是x的二次函数,再对各选项逐一判断.
2.【答案】D
【解析】【解答】解:∵抛物线的解析式为,
∴抛物线的顶点坐标为(-1,-2),
故答案为:D.
【分析】利用抛物线的顶点式直接求出顶点坐标即可.
3.【答案】B
【解析】【解答】解: 抛物线向右平移2个单位,再向下平移3个单位后的解析式为 .
故答案为:B.
【分析】 抛物线平移规律:左加右减,上加下减,据此解答即可.
4.【答案】A
【解析】【解答】解:令 ,
则
=
∴抛物线 与 轴的交点坐标是(0,-3),
故答案为:A.
【分析】由题意令x=0可得y的值,则抛物线与y轴的交点坐标可求解.
5.【答案】B
【解析】【解答】解:y=x2-8x+16-16-9=(x-4)2-25.
故答案为:B.
【分析】利用配方法将函数解析式转化为y=a(x-h)2+k的形式.
6.【答案】B
【解析】【解答】将y=0代入可得,
∵△=b2-4ac=42-4×(-1)×(-4)=16-16=0,
∴一元二次方程有两个相等的实数根,
∴抛物线与x轴的公共点个数是1个,
故答案为:B.
【分析】将二次函数与x轴的交点个数的问题转换为一元二次方程根的判别式分析求解即可.
7.【答案】B
【解析】【解答】解:
对称轴为.
a=1>0,抛物线开口向上,
所以点到对称轴距离越远,对应的函数值越大.
∵A到对称轴距离:;B到对称轴距离:;C到对称轴距离:;
∴.
故答案为:B.
【分析】求出抛物线的对称轴,根据点到对称轴的距离以及抛物线的开口方向即可判断函数值的大小.
8.【答案】B
【解析】【解答】解:∵ 实心球飞行高度y(米)与水平距离x(米)之间的关系为,铅球落地点y=0,
∴
解得:x=-2(舍去),x=10,
则该生此次实心球训练的成绩为10米.
故答案为:B.
【分析】根据解析式和铅球的落地点y=0,可得,据此求出x的值再选择.
9.【答案】D
【解析】【解答】∵二次函数的对称轴为,
∴b=1,
∴,
∴当x=1时,y有最大值,
①当时,y的最大值为2n,即x=1时,2n=,解得:n=;
当x=m时,y有最小值为2m,即,解得:m1=-2,m2=0(舍),
∴m+n=-2+;
②当时,y的最大值为2m,即x=1时,2m=,解得:m=;
当x=n时,y有最小值为2m,即,解得:n1=2,n2=-1(舍),
∴m+n=2+;
综上,的值为或.
【分析】分类讨论:①当时,y的最大值为2n,②当时,y的最大值为2m,再分别求出m、n的值,最后求出的值即可.
10.【答案】D
【解析】【解答】解:在中,
当,,
解得,,
,,
当时,,
∴原抛物线与轴交点坐标为,
∴翻折后与y轴的交点坐标为,
当直线经过点B时,直线与新图有3个交点,如图所示:
把代入中,得,
∵抛物线翻折到x轴下方的部分的解析式为:,
∴翻折后的部分解析式为:,
当直线与抛物线只有一个交点C时,
直线与图象有3个交点,
把代入中,
得到方程有两个相等的实数根,
整理得,
∴,
解得,
∴当直线与新图象有4个交点时,m的取值范围是.
故答案为:D.
【分析】令,代入可得,,如图,过点B作直线,代入可得,将直线往下平移,当直线与翻折后抛物线部分解析式只有一个交点C时,直线与图象有3个交点,结合图像可得,根据判别式即可求得,观察图像,可知一次函数在这两条直线间与新图象有4个交点,据此即可求解。
11.【答案】8
【解析】【解答】∵ ,
∴ 有最大值,
当 时, 有最大值8.
故答案为8.
【分析】二次函数的顶点式 在x=h时有最值,a>0时有最小值,a<0时有最大值,题中函数 ,故其在 时有最大值.
12.【答案】9
【解析】【解答】解:根据题意,顶点在x轴上,顶点纵坐标为0,
即
解得:c=9,
故答案为:9.
【分析】根据顶点在x轴上,可得顶点的纵坐标是0,结合顶点坐标公式,代入求解即可.
13.【答案】﹣1≤x≤3
【解析】【解答】解:∵y=kx+m与y=-kx+m的图象关于y轴对称
∴直线y=-kx+m与抛物线 y=ax2+c的交点A‘,B’与点A、B也关于y轴对称,
如图所示:
∵A(﹣3,y1)、B(1,y2)
∴A'( 3, y1 ),B'(-1,y2),
根据函数图象得:不等式 ax2+c≥﹣kx+m 的解集是 ﹣1≤x≤3 .
故答案为: ﹣1≤x≤3.
【分析】y=kx+m与y=-kx+m的图象关于y轴对称,利用数形结合思想,把不等式的解集转化为图象的交点问题求解。
14.【答案】2
【解析】【解答】解:当时,,
∴,
抛物线的对称轴为,
又轴交抛物线于点B,
∴,
∴的面积是.
故答案为:2.
【分析】先求出点A的坐标和抛物线的对称轴,再根据抛物线的对称性求出点B的坐标,最后根据三角形的面积公式求解即可.
15.【答案】
【解析】【解答】解:如图,
由题意可知C(3,1.8),
设抛物线的解析式为y=a(x﹣3)2+1.8,
把A(0,0.9)代入y=a(x﹣3)2+1.8,得
a=﹣0.1,
∴所求的抛物线的解析式是y=﹣0.1(x﹣3)2+1.8,
当y=1.4时,﹣0.1(x﹣3)2+1.8=1.4,
解得x1=1,x2=5,
∴则m的取值范围是1<m<5.
故答案为:1<m<5.
【分析】先确定顶点C的坐标,设二次函数的解析式为顶点式,再把A(0,0.9)代入求出a=﹣0.1,写出解析式求解即可。
16.【答案】;
【解析】【解答】解:(1),
当时,,
∴.
故答案为:
(2)设,则,
∴令四边形周长为,,
∵,
∴时,取最大值,为.
故答案为:
【分析】(1)令x=0,即可求得抛物线与y轴的交点B的坐标;
(2)设,则,可得四边形周长,根据函数的最大值,求得 则四边形周长的最大值为。
17.【答案】解:设解析式为:y=a(x+2)2﹣3,
将(﹣3,﹣2)代入得出:﹣2=a(﹣3+2)2﹣3,
解得:a=1.
故这个二次函数的解析式为:y=(x+2)2﹣3.
【解析】【分析】利用待定系数法求出二次函数解析式即可.
18.【答案】(1)向下
(2)x=﹣1
(3)
【解析】【解题】 应改为 , 列表如下:
描点、连线如下图,
【分析】(1)根据列表、描点、连线画出函数图象,即可求解;
(2)根据函数图象即可求解;
(3)根据函数图象的几何变换“上加下减、左加右减”即可求解.
19.【答案】(1)解:∵ 的图象经过,代入得
,
.
(2)解:当时,
∴P(2,3)是在这个二次函数的图象上.
【解析】【分析】(1)把点A坐标带入二次函数的解析式即可求出b的值;
(2)把x=2代入二次函数的解析式,若y值等于3,则说明在函数图象上,否则就不在.
20.【答案】(1)解:抛物线与轴交于点,∴
∵当时,随的增大而减小,当时,随的增大而增大,
∴抛物线对称轴为:,∴,解得:.
(2)解:由(1)知,抛物线的解析式为:.
∵点在抛物线上,∴.
原式,将代入可得,
原式
,
∴的值为.
21.【答案】(1)解:在一次函数,
令时,,
∴,
将代入中,可得:,
解得:;
(2)解:∵,,
∴,
选择扣球,则令,即:,解得:,
即:落地点距离点距离为,
∴落地点到C点的距离为,
选择吊球,则令,即:,
解得:(不合题意,舍去),
即:落地点距离点距离为,
∴落地点到C点的距离为,
∵,
∴选择吊球,使球的落地点到C点的距离更近.
(3)大
【解析】【解答】(3)解:∵,,
∴,
∴点C的坐标为,
设抛物线的解析式为,把点P和点C的坐标代入得到,
解得,
即此时抛物线的解析式为,
∴此次飞行路线的最高点是,
∴此次羽毛球飞行到最高点时与y轴的水平距离为,
即此次羽毛球飞行到最高点时与y轴的水平距离比大.
故答案为:大
【分析】(1)对于一次函数,令x=0,可求得点P的坐标,再代入二次函数即可求得的值;
(2)由题意可知OC=5,令y=0,代入两个函数的解析式,建立方程,即可求得落地点到O点的距离,即可判断谁更近;
(3)用待定系数法求出此时抛物线的解析式,确定此次飞行路线的最高点的坐标,即可得到答案.
22.【答案】(1)解:设抛物线的解析式为y=ax2+bx+c(a≠0),
在等腰Rt△ABC中,OC垂直平分AB,且AB=4,
∴OA=OB=OC=2,
∴A(﹣2,0),B(2,0),C(0,﹣2),代入解析式得:
,
解得,,
∴抛物线的解析式为y=﹣2;
(2)解:①设直线l的解析式为y=kx,M(x1,y1),N(x2,y2),
由 , 可得
∴x1+x2=2k,x1 x2=﹣4,
∴,
∴,
∴,
∴当k=0时2取最小值为4.
∴△CMN面积的最小值为4.
②存在,点P(,﹣),直线l的解析式为y=(1﹣)x或点P(﹣,﹣),直线l的解析式为y=(1+)x.
【解析】【解题】(2) ② 设抛物线上存在点P(a,), 使得点P与点Q关于直线l对称,
可得PO=PQ,
解得:
(不合题意,舍去),
当时,点
线段PQ的中点为
直线l的表达式为:
当时,点
线段PQ的中点为
直线l的表达式为:
综上所述:点直线l的表达式或.
【分析】(1) 设抛物线的解析式为y=ax2+bx+c(a≠0), 由等腰直角三角形的性质以及AB的值求得 OA=OB=OC=2, 从而得到A、B、C三点的坐标,利用待定系数法求得a、b、c的值,即可求解;
(2) ①设直线l的解析式为y=kx,M(x1,y1),N(x2,y2), 联立方程组得到 ,利用根与系数的关系得到 , 再由三角形的面积公式得到 ,从而求解;②设抛物线上存在点P(a,), 使得点P与点Q关于直线l对称,可得PO=PQ,列出关于m的方程,解得PQ的中点坐标,即可求解.
23.【答案】(1)解:∵抛物线与轴正半轴于点,
∴,
∵在中, ,
∴,
∴
把点、代入得:
解得
∴抛物线的解析式为;
(2)解:当时,
解得:,
∴,
∴,
∵点P在抛物线上,点P的横坐标为,
∴,
过点P作轴于点L,
∴,
∴;
(3)解:∵,
∴,
过点K作于点M,交于点N,作于点G,
根据对称性可知:,, ,
∵,
∴,
∴,
设,
∴,
∵,
∴,
∴
,
∴,
∴,
过点D作,
∵,,,
∴,
∴,,
过点F作于T,
∵,
∴与都是等腰直角三角形,
∴,,,
∵,,
∴
∵点P的横坐标为t,
∴,
∴,
∴,
∴,
解得:,
,
∴.
【解析】【分析】(1)根据已知的锐角三角函数可求出点C的坐标,然后用待定系数法可求解;
(2)令解析式中的y=0可得关于x的一元二次方程,解方程可求出点B的坐标,过点P作Pl⊥x轴于点L,用含t的代数式将PL表示出来,然后根据三角形的面积公式即可求解;
(3)由题意将所求出的二次函数的解析式配成顶点式可得顶点K的坐标,过点K作KM⊥AB于点M,交DF于点N,作FG⊥AK于点G,结合轴对称的性质可证△DHK≌△BEF,则可得DH=BE,HK=EF,过点F作FT⊥KM于T,易证△FTN和△HND是等腰直角三角形,于是可得DH=HN,FT=EM=TN,EF=MT=HK,根据线段的构成Mk=HK+HN+TN+MT可得关于t的方程,解方程即可求出t的值,于是点P的坐标可求解..
1 / 1
同课章节目录
