浙教版八年级下册3.3 方差和标准差 课件(18张PPT)
文档属性
| 名称 | 浙教版八年级下册3.3 方差和标准差 课件(18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 742.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 22:59:25 | ||
图片预览


文档简介
(共18张PPT)
单/击/此/处/添/加/副/标/题/内/容
方差与标准差
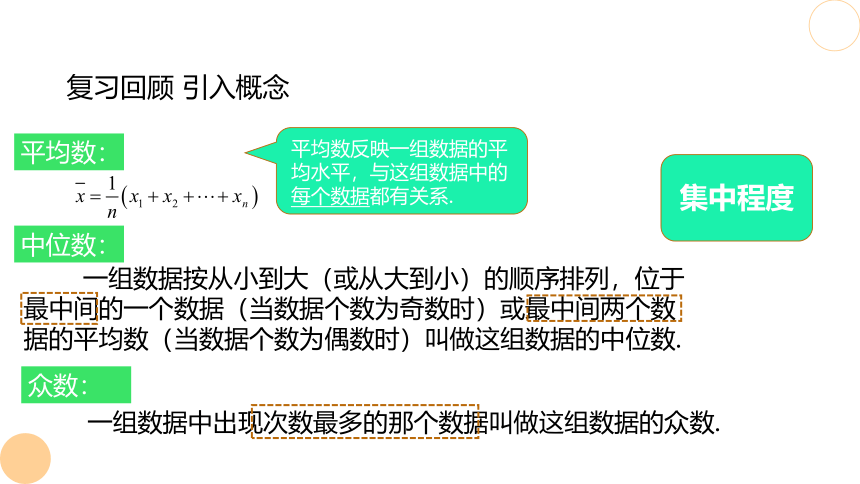
平均数:
复习回顾 引入概念
中位数:
众数:
一组数据中出现次数最多的那个数据叫做这组数据的众数.
一组数据按从小到大(或从大到小)的顺序排列,位于最中间的一个数据(当数据个数为奇数时)或最中间两个数据的平均数(当数据个数为偶数时)叫做这组数据的中位数.
集中程度
平均数反映一组数据的平均水平,与这组数据中的每个数据都有关系.
复习回顾 引入概念
如果要选拔射击手参加射击比赛,
甲、乙两人的测试成绩统计如下:
问题1:请分别算出甲、乙两人的平均成绩.
选谁去参加比赛呢?
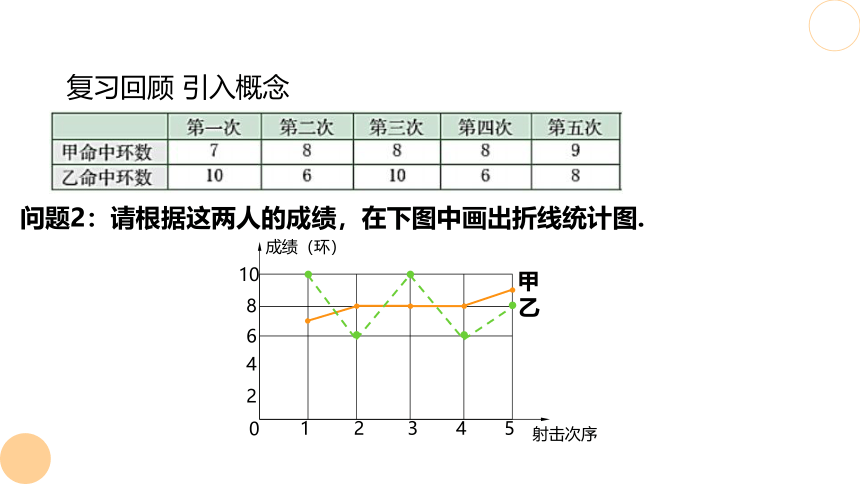
复习回顾 引入概念
问题2:请根据这两人的成绩,在下图中画出折线统计图.
0
1
2
2
3
4
5
4
6
8
10
射击次序
成绩(环)
甲
乙
复习回顾 引入概念
问题3:现要从甲、乙两人中挑选一人参加比赛,你认为挑选哪一位比较适宜?
0
1
2
2
3
4
5
4
6
8
10
射击次序
成绩(环)
甲
乙
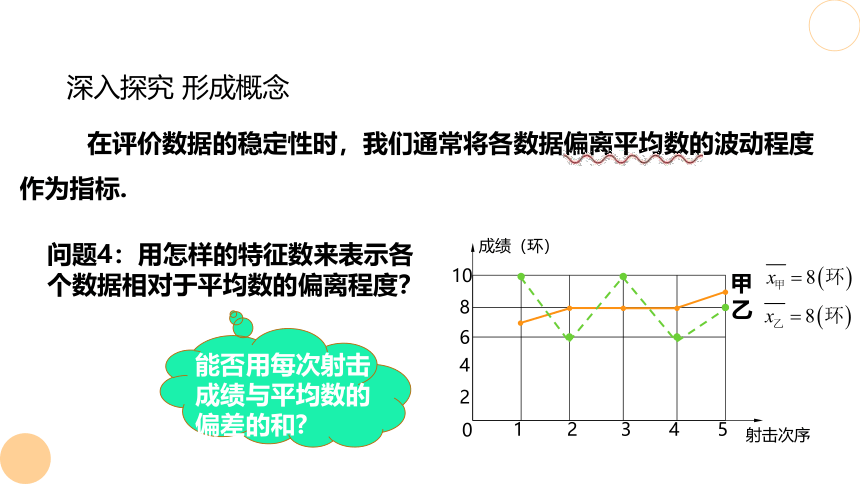
问题4:用怎样的特征数来表示各个数据相对于平均数的偏离程度?
在评价数据的稳定性时,我们通常将各数据偏离平均数的波动程度作为指标.
能否用每次射击成绩与平均数的偏差的和
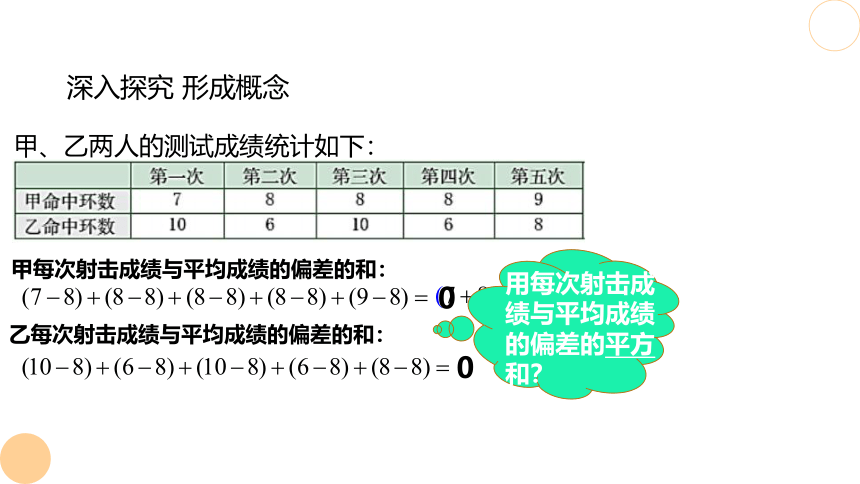
深入探究 形成概念
0
1
2
2
3
4
5
4
6
8
10
射击次序
成绩(环)
甲
乙
甲每次射击成绩与平均成绩的偏差的和:
乙每次射击成绩与平均成绩的偏差的和:
0
0
甲、乙两人的测试成绩统计如下:
用每次射击成绩与平均成绩的偏差的平方和?
深入探究 形成概念
甲每次射击成绩与平均成绩的偏差的平方和:
甲、乙两人的测试成绩统计如下:
乙每次射击成绩与平均成绩的偏差的平方和:
问题5:上述各偏差的平方和的大小还与什么有关?
与射击次数有关!
深入探究 形成概念
2
16
用各偏差平方和的平均数来衡量数据的稳定性.
一般地,各数据与平均数的差的平方的平均数叫做这组数据的 .
方差
注:方差越大,说明数据的波动越大,越不稳定.
深入探究 形成概念
离散程度
甲、乙两人的测试成绩统计如下:
方差的单位是所给数据单位的平方.
深入探究 形成概念
为了使单位一致,可用方差的算术平方根来表示数据的稳定性.
一般地,一组数据的方差的算术平方根称为这组数据的 .
标准差
深入探究 形成概念
标准差:
深入探究 形成概念
方差:
离散程度
探究提升 体悟概念
例 为了考察甲、乙两块地小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):
甲: 12,13,14,15,10,16,13,11,15,11;
乙: 11,16,17,14,13,19,6,8,10,16.
哪块地小麦长得比较整齐
解:
因为 ,所以甲这块地的小麦长得比较整齐.
探究提升 体悟概念
12,13,14,15,10,16,13,11,15,11.
把这组数据的每个数都减去5,得到一组新数据:
7,8,9,10,5,11,8,6,11,6.
问题1:请将这两组数据画成折线图, 并用一条平行于横轴的直线来表示这两组数据的平均数.
5
1
2
11
3
4
5
12
13
14
15
数据序号
数据
16
6
8
7
9
10
6
7
8
9
10
问题2:观察你画的两个图形,你发现了哪些有趣的结论?
1 复习回顾 引入概念
3 探究提升 体悟概念
2 深入探究 形成概念
标准差:
方差:
离散程度
中位数
众数
平均数
集中程度
数形结合
课后作业
1. 某校举办了一次趣味数学竞赛,满分100分,学生得分均为整数,达到成绩60分及以上为合格,达到90分及以上为优秀,这次竞赛中,甲、乙两组学生成绩如下(单位:分)
甲组:30,60,60,60,60,60,70,90,90,100;
乙组:50,60,60,60,70,70,70,70,80,90.
如果你是该校数学竞赛的教练员,现在需要你根据成绩的稳定性选一组同学代表学校参加复赛,你会选择哪一组?并说明理由.
课后作业
2. 某公司计划从两家生产能力相近的制造厂选择一家来承担外销业务,这两家厂生产的皮具款式和材料都符合要求,因此只需要检测皮具质量的克数是否稳定,现从两家提供的样品中各随机抽取了6件进行检查,超过标准质量部分记为正数,不足部分记为负数,若该皮具的标准质量为400克,测得它们质量如下(单位:g).
(1)分别计算甲、乙两厂抽样检测的6件皮具的平均质量各是多少克?
(2)通过计算,你认为哪一家生产的皮具质量比较稳定?
厂家 超过标准质量的部分 甲 ﹣4 1 0 1 2 0
乙 ﹣2 1 ﹣1 0 1 1
课后作业
3. 阅读以下材料:
已知一组数据 ,把每个数据都乘以2,
得到一组新数据 .
设原数据的平均数和方差分别为 ,可得新数据的平均数为:
请回答:已知数据 的平均数是3,方差是2,
则 的平均数和方差分别为__________.
新数据的方差
单/击/此/处/添/加/副/标/题/内/容
方差与标准差
平均数:
复习回顾 引入概念
中位数:
众数:
一组数据中出现次数最多的那个数据叫做这组数据的众数.
一组数据按从小到大(或从大到小)的顺序排列,位于最中间的一个数据(当数据个数为奇数时)或最中间两个数据的平均数(当数据个数为偶数时)叫做这组数据的中位数.
集中程度
平均数反映一组数据的平均水平,与这组数据中的每个数据都有关系.
复习回顾 引入概念
如果要选拔射击手参加射击比赛,
甲、乙两人的测试成绩统计如下:
问题1:请分别算出甲、乙两人的平均成绩.
选谁去参加比赛呢?
复习回顾 引入概念
问题2:请根据这两人的成绩,在下图中画出折线统计图.
0
1
2
2
3
4
5
4
6
8
10
射击次序
成绩(环)
甲
乙
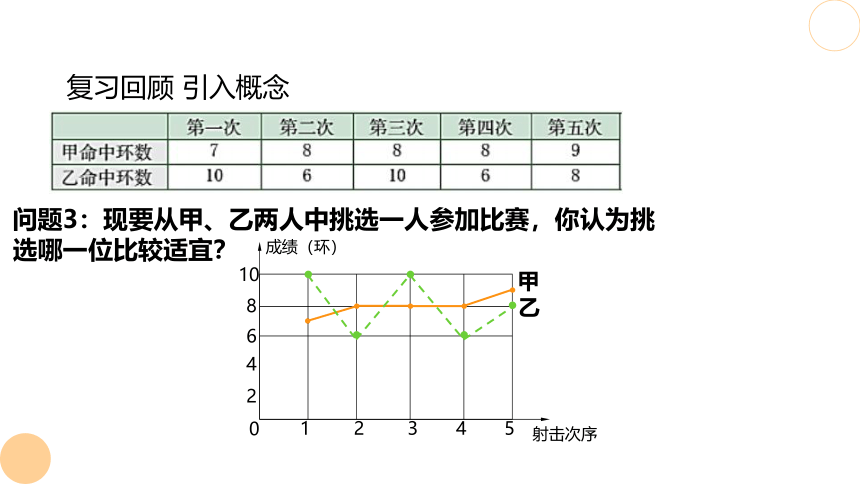
复习回顾 引入概念
问题3:现要从甲、乙两人中挑选一人参加比赛,你认为挑选哪一位比较适宜?
0
1
2
2
3
4
5
4
6
8
10
射击次序
成绩(环)
甲
乙
问题4:用怎样的特征数来表示各个数据相对于平均数的偏离程度?
在评价数据的稳定性时,我们通常将各数据偏离平均数的波动程度作为指标.
能否用每次射击成绩与平均数的偏差的和
深入探究 形成概念
0
1
2
2
3
4
5
4
6
8
10
射击次序
成绩(环)
甲
乙
甲每次射击成绩与平均成绩的偏差的和:
乙每次射击成绩与平均成绩的偏差的和:
0
0
甲、乙两人的测试成绩统计如下:
用每次射击成绩与平均成绩的偏差的平方和?
深入探究 形成概念
甲每次射击成绩与平均成绩的偏差的平方和:
甲、乙两人的测试成绩统计如下:
乙每次射击成绩与平均成绩的偏差的平方和:
问题5:上述各偏差的平方和的大小还与什么有关?
与射击次数有关!
深入探究 形成概念
2
16
用各偏差平方和的平均数来衡量数据的稳定性.
一般地,各数据与平均数的差的平方的平均数叫做这组数据的 .
方差
注:方差越大,说明数据的波动越大,越不稳定.
深入探究 形成概念
离散程度
甲、乙两人的测试成绩统计如下:
方差的单位是所给数据单位的平方.
深入探究 形成概念
为了使单位一致,可用方差的算术平方根来表示数据的稳定性.
一般地,一组数据的方差的算术平方根称为这组数据的 .
标准差
深入探究 形成概念
标准差:
深入探究 形成概念
方差:
离散程度
探究提升 体悟概念
例 为了考察甲、乙两块地小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):
甲: 12,13,14,15,10,16,13,11,15,11;
乙: 11,16,17,14,13,19,6,8,10,16.
哪块地小麦长得比较整齐
解:
因为 ,所以甲这块地的小麦长得比较整齐.
探究提升 体悟概念
12,13,14,15,10,16,13,11,15,11.
把这组数据的每个数都减去5,得到一组新数据:
7,8,9,10,5,11,8,6,11,6.
问题1:请将这两组数据画成折线图, 并用一条平行于横轴的直线来表示这两组数据的平均数.
5
1
2
11
3
4
5
12
13
14
15
数据序号
数据
16
6
8
7
9
10
6
7
8
9
10
问题2:观察你画的两个图形,你发现了哪些有趣的结论?
1 复习回顾 引入概念
3 探究提升 体悟概念
2 深入探究 形成概念
标准差:
方差:
离散程度
中位数
众数
平均数
集中程度
数形结合
课后作业
1. 某校举办了一次趣味数学竞赛,满分100分,学生得分均为整数,达到成绩60分及以上为合格,达到90分及以上为优秀,这次竞赛中,甲、乙两组学生成绩如下(单位:分)
甲组:30,60,60,60,60,60,70,90,90,100;
乙组:50,60,60,60,70,70,70,70,80,90.
如果你是该校数学竞赛的教练员,现在需要你根据成绩的稳定性选一组同学代表学校参加复赛,你会选择哪一组?并说明理由.
课后作业
2. 某公司计划从两家生产能力相近的制造厂选择一家来承担外销业务,这两家厂生产的皮具款式和材料都符合要求,因此只需要检测皮具质量的克数是否稳定,现从两家提供的样品中各随机抽取了6件进行检查,超过标准质量部分记为正数,不足部分记为负数,若该皮具的标准质量为400克,测得它们质量如下(单位:g).
(1)分别计算甲、乙两厂抽样检测的6件皮具的平均质量各是多少克?
(2)通过计算,你认为哪一家生产的皮具质量比较稳定?
厂家 超过标准质量的部分 甲 ﹣4 1 0 1 2 0
乙 ﹣2 1 ﹣1 0 1 1
课后作业
3. 阅读以下材料:
已知一组数据 ,把每个数据都乘以2,
得到一组新数据 .
设原数据的平均数和方差分别为 ,可得新数据的平均数为:
请回答:已知数据 的平均数是3,方差是2,
则 的平均数和方差分别为__________.
新数据的方差
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
