浙教版八年级下册4.1 多边形 课件(19张PPT)
文档属性
| 名称 | 浙教版八年级下册4.1 多边形 课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 868.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 23:03:36 | ||
图片预览

文档简介
(共19张PPT)
多边形(第二课时)
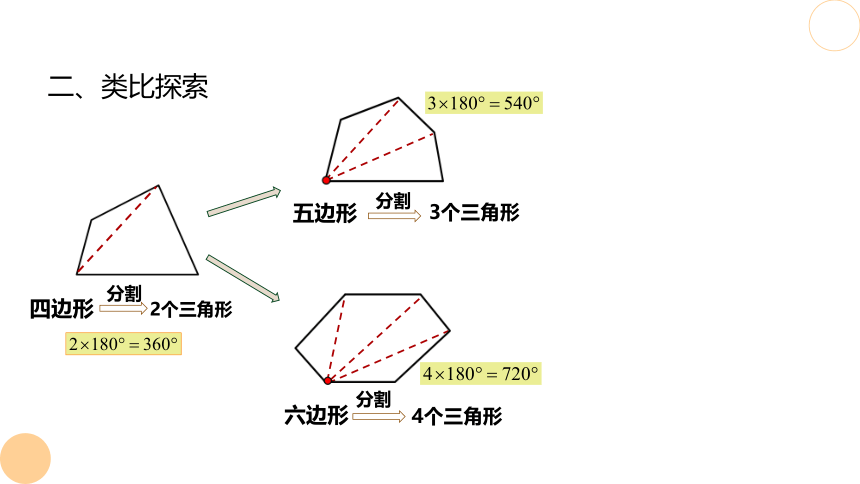
二、类比探索
四边形
分割
2个三角形
五边形
3个三角形
分割
六边形
4个三角形
分割
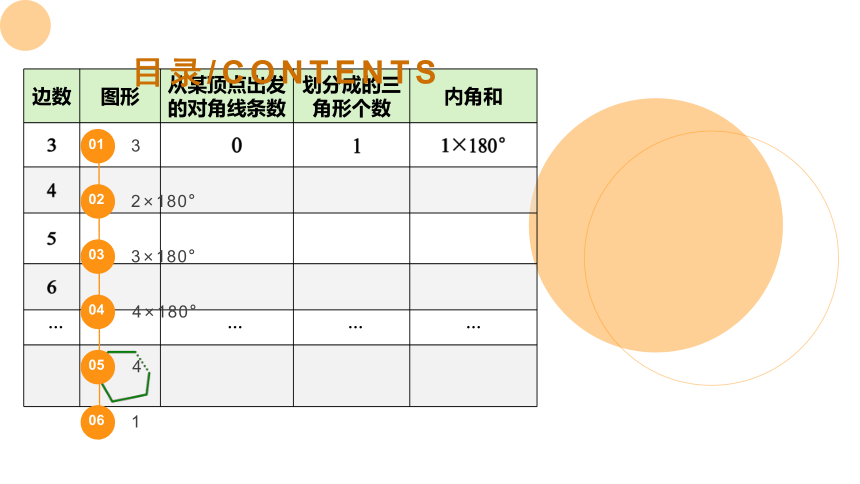
边数 图形 从某顶点出发 的对角线条数 划分成的三 角形个数 内角和
3 0 1 1×180°
4
5
6
… … … …
目录/CONTENTS
01
02
03
04
05
06
3
2×180°
3×180°
4×180°
4
1
A1
…
A2
A3
A4
An-1
An
An-2
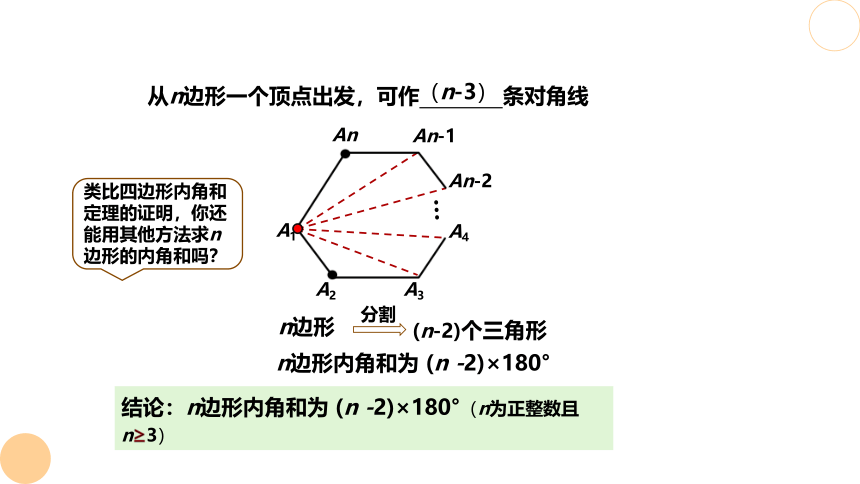
从n边形一个顶点出发,可作 条对角线
n边形
(n-2)个三角形
分割
结论:n边形内角和为 (n -2)×180°(n为正整数且n≥3)
(n-3)
类比四边形内角和定理的证明,你还能用其他方法求n边形的内角和吗?
n边形内角和为 (n -2)×180°
…
A1
A2
A3
A4
An-1
An
An-2
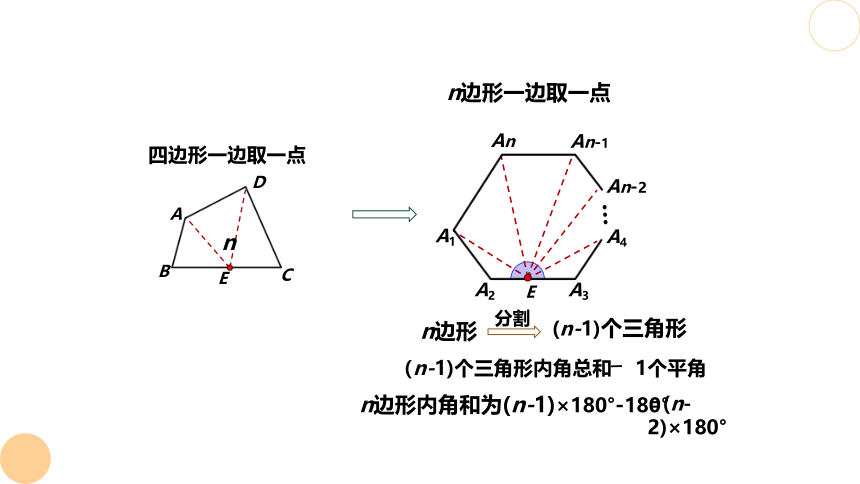
四边形一边取一点
A
B
C
D
E
n边形一边取一点
n边形
(n-1)个三角形
分割
(n-1)个三角形内角总和 1个平角
n边形内角和为(n-1)×180°-180°
=(n-2)×180°
E
n
…
A1
A2
A3
A4
An-1
An
An-2
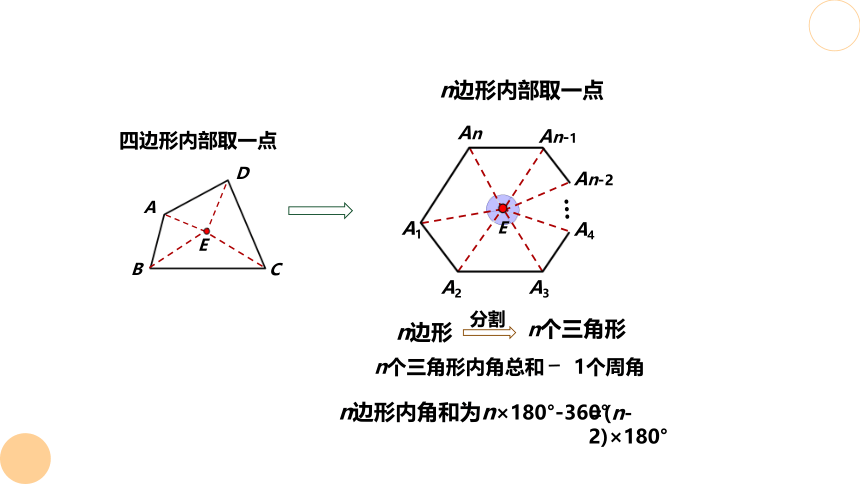
四边形内部取一点
n边形内部取一点
A
B
C
D
E
n边形
n个三角形
分割
n个三角形内角总和 1个周角
n边形内角和为n×180°-360°
=(n-2)×180°
E
…
A1
A2
A3
A4
An-1
An
An-2
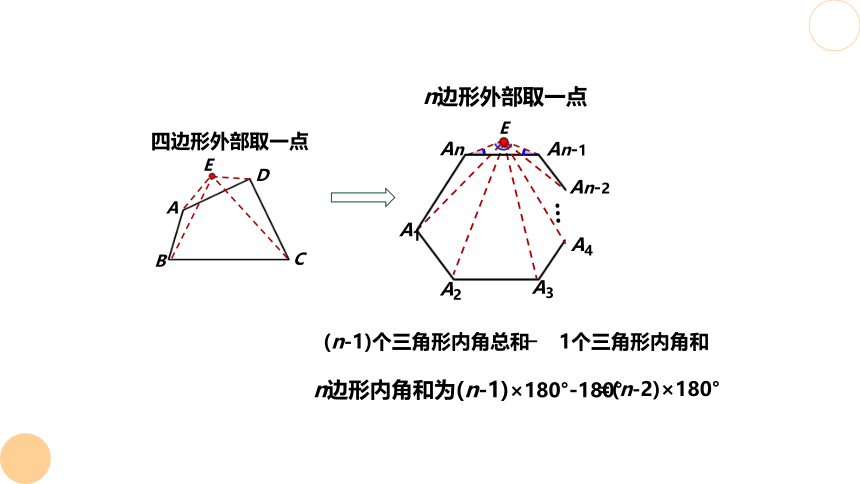
n边形外部取一点
(n-1)个三角形内角总和 1个三角形内角和
n边形内角和为(n-1)×180°-180°
=(n-2)×180°
A
B
C
D
E
四边形外部取一点
E
…
…
…
1.以上都是类比四边形内角和的证明思路,采用化归的思
想将未知的多边形问题 转化为已知的三角形问题来研究的.
2.多边形内角和仅与边数有关.
n边形内角和为 (n -2)×180°(n≥3)
…
归纳
练习 一个多边形的内角和是900° .
(1)确定这个多边形的边数.
解 (1) 设这个多边形是n边形,
所以这个多边形是七边形.
则有 (n -2)×180°=900°
解得 n=7
解(2)七边形每个顶点处的内角与外角均
互为邻补角.
其中内角和为(7-2)×180°,
外角和为 7×180°-(7-2)×180°
=360°
练习 一个多边形的内角和是900° .
(2)在多边形的每个顶点处各取一个外角,它们的和叫做这个多边形的外角和,求这个多边形的外角和.
7个内角和7个外角总和为7×180°,
追问:n边形的外角和为多少?
A1
…
追问:n边形的外角和为多少?
分析: n边形每个顶点处的内角与外角均互为邻补角.
n×180°-(n-2)×180°
=n×180°-n×180°+360°
=360°
n边形外角和为
结论:任意多边形外角和都为360°(与边数无关)
A1
任意多边形外角和等于周角的度数(360°).
追问:n边形的外角和为多少?
例1 一个六边形如图所示.已知AB∥DE,BC∥EF,CD∥AF.
求∠A+∠C+∠E的值.
三、典例精析
A
B
C
D
E
F
∠A+∠B+∠C+∠D+∠E+∠F
=(6-2)×180°=720°
这3个角和其他3个角有什么关系?
平行的条件如何利用起来?
分析
例1 一个六边形如图所示.已知AB∥DE,BC∥EF, CD∥AF. 求∠A+
∠C +∠E的值.
三、典例精析
A
B
C
D
E
F
解:
如图,连结AD.
∵AB∥DE,CD∥AF,
∴∠1=∠2,∠3=∠4.
∴∠1+∠3=∠2+∠4,
即∠FAB=∠CDE.
同理,∠B=∠E,∠C=∠F.
∵∠FAB+∠B+∠C+∠CDF+∠E+∠F
=
(6-2)×180°=720°
∴∠FAB+∠C+∠E=
=360°.
1
2
3
4
方法一
例1 一个六边形如图所示.已知AB∥DE,BC∥EF,
CD∥AF. 求∠A+∠C+∠E的值.
三、典例精析
A
B
C
D
E
F
G
A
B
C
D
E
F
1
2
3
4
以AD所在直线为截线
以AF、DE所在直线为截线
例1 一个六边形如图所示.已知AB∥DE,BC∥EF, CD∥AF. 求∠A+∠C+∠E的值.
三、典例精析
A
B
C
D
E
F
G
解:
如图,分别延长AF,DE交于点G.
∵AB∥DE,
∴∠G+∠A=180°.
∵CD∥AF,
∴∠G+∠D=180°.
∴∠A=∠D.
同理,∠B=∠DEF,∠C=∠EFA.
∴∠FAB+∠C+∠E=
=360°.
方法二
四、小结提升
本节课我们是怎样展开学习的?你收获了哪些数学知识和数学思想?
类比
四边形
内角和
特殊到一般
…
化归
转化为三角形问题
特殊到一般
方 程
五、作业布置
(1)课本P80作业题第2、4题;
(2)一个六边形如图所示.已知∠B=∠E,∠A=∠D,BC∥EF,
求∠A+∠C+∠E的度数.
选做题
必做题
一个多边形剪去一个角后内角和为1800°,则原多边形是
几边形?
感 谢 聆 听
汇报人姓名
多边形(第二课时)
二、类比探索
四边形
分割
2个三角形
五边形
3个三角形
分割
六边形
4个三角形
分割
边数 图形 从某顶点出发 的对角线条数 划分成的三 角形个数 内角和
3 0 1 1×180°
4
5
6
… … … …
目录/CONTENTS
01
02
03
04
05
06
3
2×180°
3×180°
4×180°
4
1
A1
…
A2
A3
A4
An-1
An
An-2
从n边形一个顶点出发,可作 条对角线
n边形
(n-2)个三角形
分割
结论:n边形内角和为 (n -2)×180°(n为正整数且n≥3)
(n-3)
类比四边形内角和定理的证明,你还能用其他方法求n边形的内角和吗?
n边形内角和为 (n -2)×180°
…
A1
A2
A3
A4
An-1
An
An-2
四边形一边取一点
A
B
C
D
E
n边形一边取一点
n边形
(n-1)个三角形
分割
(n-1)个三角形内角总和 1个平角
n边形内角和为(n-1)×180°-180°
=(n-2)×180°
E
n
…
A1
A2
A3
A4
An-1
An
An-2
四边形内部取一点
n边形内部取一点
A
B
C
D
E
n边形
n个三角形
分割
n个三角形内角总和 1个周角
n边形内角和为n×180°-360°
=(n-2)×180°
E
…
A1
A2
A3
A4
An-1
An
An-2
n边形外部取一点
(n-1)个三角形内角总和 1个三角形内角和
n边形内角和为(n-1)×180°-180°
=(n-2)×180°
A
B
C
D
E
四边形外部取一点
E
…
…
…
1.以上都是类比四边形内角和的证明思路,采用化归的思
想将未知的多边形问题 转化为已知的三角形问题来研究的.
2.多边形内角和仅与边数有关.
n边形内角和为 (n -2)×180°(n≥3)
…
归纳
练习 一个多边形的内角和是900° .
(1)确定这个多边形的边数.
解 (1) 设这个多边形是n边形,
所以这个多边形是七边形.
则有 (n -2)×180°=900°
解得 n=7
解(2)七边形每个顶点处的内角与外角均
互为邻补角.
其中内角和为(7-2)×180°,
外角和为 7×180°-(7-2)×180°
=360°
练习 一个多边形的内角和是900° .
(2)在多边形的每个顶点处各取一个外角,它们的和叫做这个多边形的外角和,求这个多边形的外角和.
7个内角和7个外角总和为7×180°,
追问:n边形的外角和为多少?
A1
…
追问:n边形的外角和为多少?
分析: n边形每个顶点处的内角与外角均互为邻补角.
n×180°-(n-2)×180°
=n×180°-n×180°+360°
=360°
n边形外角和为
结论:任意多边形外角和都为360°(与边数无关)
A1
任意多边形外角和等于周角的度数(360°).
追问:n边形的外角和为多少?
例1 一个六边形如图所示.已知AB∥DE,BC∥EF,CD∥AF.
求∠A+∠C+∠E的值.
三、典例精析
A
B
C
D
E
F
∠A+∠B+∠C+∠D+∠E+∠F
=(6-2)×180°=720°
这3个角和其他3个角有什么关系?
平行的条件如何利用起来?
分析
例1 一个六边形如图所示.已知AB∥DE,BC∥EF, CD∥AF. 求∠A+
∠C +∠E的值.
三、典例精析
A
B
C
D
E
F
解:
如图,连结AD.
∵AB∥DE,CD∥AF,
∴∠1=∠2,∠3=∠4.
∴∠1+∠3=∠2+∠4,
即∠FAB=∠CDE.
同理,∠B=∠E,∠C=∠F.
∵∠FAB+∠B+∠C+∠CDF+∠E+∠F
=
(6-2)×180°=720°
∴∠FAB+∠C+∠E=
=360°.
1
2
3
4
方法一
例1 一个六边形如图所示.已知AB∥DE,BC∥EF,
CD∥AF. 求∠A+∠C+∠E的值.
三、典例精析
A
B
C
D
E
F
G
A
B
C
D
E
F
1
2
3
4
以AD所在直线为截线
以AF、DE所在直线为截线
例1 一个六边形如图所示.已知AB∥DE,BC∥EF, CD∥AF. 求∠A+∠C+∠E的值.
三、典例精析
A
B
C
D
E
F
G
解:
如图,分别延长AF,DE交于点G.
∵AB∥DE,
∴∠G+∠A=180°.
∵CD∥AF,
∴∠G+∠D=180°.
∴∠A=∠D.
同理,∠B=∠DEF,∠C=∠EFA.
∴∠FAB+∠C+∠E=
=360°.
方法二
四、小结提升
本节课我们是怎样展开学习的?你收获了哪些数学知识和数学思想?
类比
四边形
内角和
特殊到一般
…
化归
转化为三角形问题
特殊到一般
方 程
五、作业布置
(1)课本P80作业题第2、4题;
(2)一个六边形如图所示.已知∠B=∠E,∠A=∠D,BC∥EF,
求∠A+∠C+∠E的度数.
选做题
必做题
一个多边形剪去一个角后内角和为1800°,则原多边形是
几边形?
感 谢 聆 听
汇报人姓名
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
