浙教版八年级下册第四章 平行四边形 小结 课件(15张PPT)
文档属性
| 名称 | 浙教版八年级下册第四章 平行四边形 小结 课件(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 795.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
平行四边形小结
最近,冯老师家在装修,我想在花园里造一条石头小路,计划在小路的正中央铺上平行四边形的石砖(形状不限),供人行走.
A
B
C
D
∟
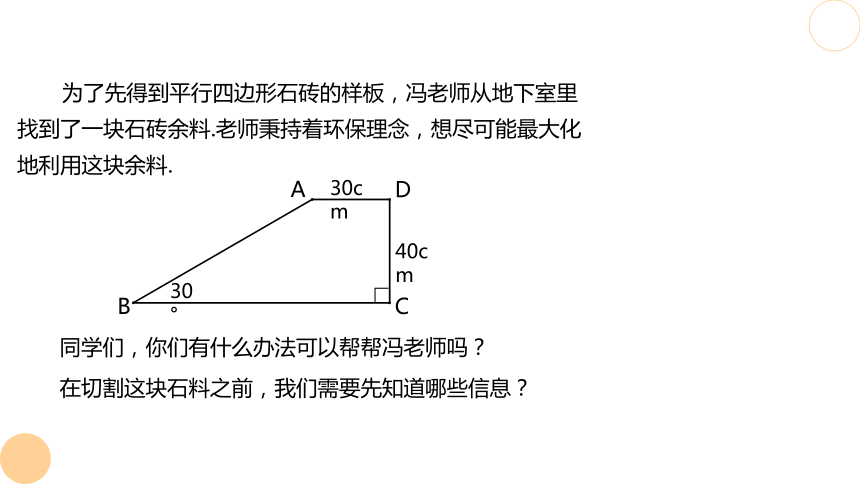
为了先得到平行四边形石砖的样板,冯老师从地下室里找到了一块石砖余料.老师秉持着环保理念,想尽可能最大化地利用这块余料.
同学们,你们有什么办法可以帮帮冯老师吗?
在切割这块石料之前,我们需要先知道哪些信息?
30°
30cm
40cm
探究:画一画
画法一
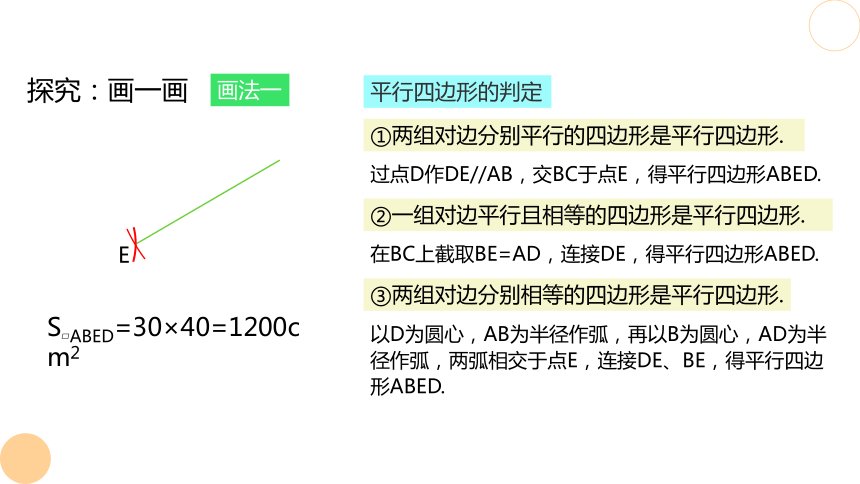
平行四边形的判定
②一组对边平行且相等的四边形是平行四边形.
在BC上截取BE=AD,连接DE,得平行四边形ABED.
①两组对边分别平行的四边形是平行四边形.
过点D作DE//AB,交BC于点E,得平行四边形ABED.
E
③两组对边分别相等的四边形是平行四边形.
以D为圆心,AB为半径作弧,再以B为圆心,AD为半径作弧,两弧相交于点E,连接DE、BE,得平行四边形ABED.
S ABED=30×40=1200cm2
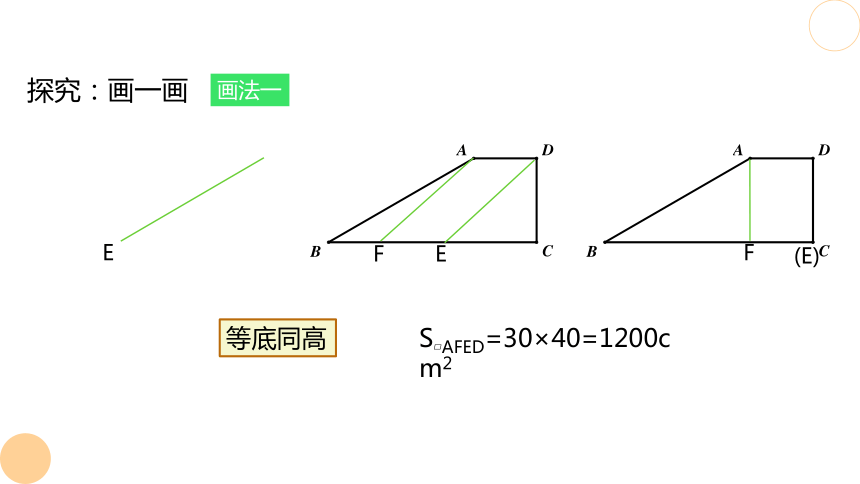
等底同高
F
E
F
画法一
探究:画一画
(E)
S AFED=30×40=1200cm2
E
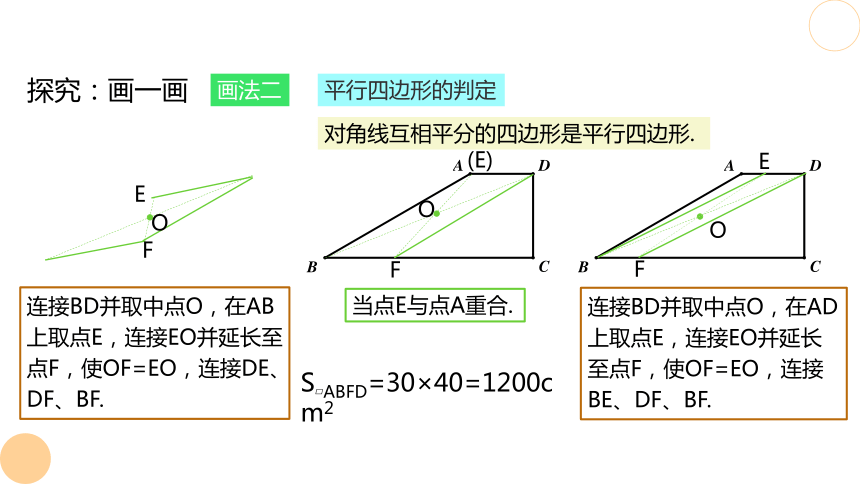
平行四边形的判定
对角线互相平分的四边形是平行四边形.
E
F
连接BD并取中点O,在AB上取点E,连接EO并延长至点F,使OF=EO,连接DE、DF、BF.
O
画法二
探究:画一画
E
F
O
F
O
(E)
连接BD并取中点O,在AD上取点E,连接EO并延长至点F,使OF=EO,连接BE、DF、BF.
当点E与点A重合.
S ABFD=30×40=1200cm2
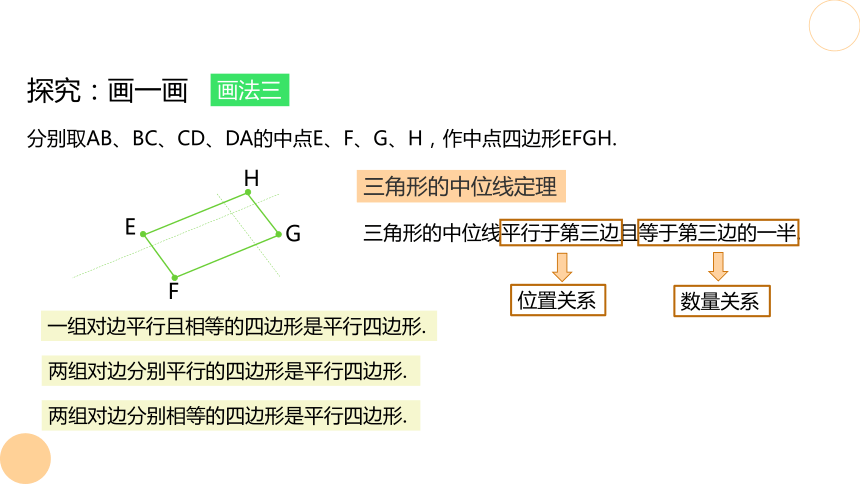
一组对边平行且相等的四边形是平行四边形.
两组对边分别平行的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
三角形的中位线平行于第三边且等于第三边的一半.
E
F
G
H
分别取AB、BC、CD、DA的中点E、F、G、H,作中点四边形EFGH.
画法三
探究:画一画
位置关系
数量关系
三角形的中位线定理
怎么得到平行四边形EFGH的面积呢?
∴S EFGH=S梯形ABCD-S△AEF-S△FDG-S△GCH-S△HBE
画法三
探究:画一画
N
M
过点E作MN BC,交BC于N,交DA延长线于M.
∵△AME≌△BNE ∴EN=EM=20cm
割补法
E
在CD上任取一点E,作EF//BC,交AB于点F,作EG//AB,交BC于点G,得平行四边形BFEG.
两组对边分别平行的四边形是平行四边形.
F
G
∴S BFEG
配方法
∴Smax
画法四
探究:画一画
30°
E
在CD上任取一点E,连接AE,作EF//AB,交BC于点F,作FG//AE,交AB于点G,得平行四边形AEFG.
两组对边分别平行的四边形是平行四边形.
F
G
∴S AEFG
画法四
探究:画一画
∴Smax
配方法
30°
H
∟
在面积相等的情况下,该如何挑选平行四边形的形状,使花园小路更加美观呢?
探究:选一选
等积变形
于是冯老师决定,就以平行四边形FEGH为花园小路的样板!
“匀称、工整、美观”
探究:选一选
再回首
判定
性质
平行四边形的判定
边 两组对边分别平行的四边形
两组对边分别相等的四边形
一组对边平行且相等的四边形
对角线 对角线互相平分的四边形
平行四边形的性质
边 对边平行且相等
角 对角相等,邻角互补
对角线 对角线互相平分
对称性 中心对称图形
数学知识
数学方法
配方法
等积变形
数学思想
数形结合
转化
分类讨论
平行四边形
矩形
菱形
会用数学的眼光观察现实世界!
会用数学的思维思考现实世界!
会用数学的语言表达现实世界!
齐展望
……
谢 谢 大 家 !
汇报人姓名
平行四边形小结
最近,冯老师家在装修,我想在花园里造一条石头小路,计划在小路的正中央铺上平行四边形的石砖(形状不限),供人行走.
A
B
C
D
∟
为了先得到平行四边形石砖的样板,冯老师从地下室里找到了一块石砖余料.老师秉持着环保理念,想尽可能最大化地利用这块余料.
同学们,你们有什么办法可以帮帮冯老师吗?
在切割这块石料之前,我们需要先知道哪些信息?
30°
30cm
40cm
探究:画一画
画法一
平行四边形的判定
②一组对边平行且相等的四边形是平行四边形.
在BC上截取BE=AD,连接DE,得平行四边形ABED.
①两组对边分别平行的四边形是平行四边形.
过点D作DE//AB,交BC于点E,得平行四边形ABED.
E
③两组对边分别相等的四边形是平行四边形.
以D为圆心,AB为半径作弧,再以B为圆心,AD为半径作弧,两弧相交于点E,连接DE、BE,得平行四边形ABED.
S ABED=30×40=1200cm2
等底同高
F
E
F
画法一
探究:画一画
(E)
S AFED=30×40=1200cm2
E
平行四边形的判定
对角线互相平分的四边形是平行四边形.
E
F
连接BD并取中点O,在AB上取点E,连接EO并延长至点F,使OF=EO,连接DE、DF、BF.
O
画法二
探究:画一画
E
F
O
F
O
(E)
连接BD并取中点O,在AD上取点E,连接EO并延长至点F,使OF=EO,连接BE、DF、BF.
当点E与点A重合.
S ABFD=30×40=1200cm2
一组对边平行且相等的四边形是平行四边形.
两组对边分别平行的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
三角形的中位线平行于第三边且等于第三边的一半.
E
F
G
H
分别取AB、BC、CD、DA的中点E、F、G、H,作中点四边形EFGH.
画法三
探究:画一画
位置关系
数量关系
三角形的中位线定理
怎么得到平行四边形EFGH的面积呢?
∴S EFGH=S梯形ABCD-S△AEF-S△FDG-S△GCH-S△HBE
画法三
探究:画一画
N
M
过点E作MN BC,交BC于N,交DA延长线于M.
∵△AME≌△BNE ∴EN=EM=20cm
割补法
E
在CD上任取一点E,作EF//BC,交AB于点F,作EG//AB,交BC于点G,得平行四边形BFEG.
两组对边分别平行的四边形是平行四边形.
F
G
∴S BFEG
配方法
∴Smax
画法四
探究:画一画
30°
E
在CD上任取一点E,连接AE,作EF//AB,交BC于点F,作FG//AE,交AB于点G,得平行四边形AEFG.
两组对边分别平行的四边形是平行四边形.
F
G
∴S AEFG
画法四
探究:画一画
∴Smax
配方法
30°
H
∟
在面积相等的情况下,该如何挑选平行四边形的形状,使花园小路更加美观呢?
探究:选一选
等积变形
于是冯老师决定,就以平行四边形FEGH为花园小路的样板!
“匀称、工整、美观”
探究:选一选
再回首
判定
性质
平行四边形的判定
边 两组对边分别平行的四边形
两组对边分别相等的四边形
一组对边平行且相等的四边形
对角线 对角线互相平分的四边形
平行四边形的性质
边 对边平行且相等
角 对角相等,邻角互补
对角线 对角线互相平分
对称性 中心对称图形
数学知识
数学方法
配方法
等积变形
数学思想
数形结合
转化
分类讨论
平行四边形
矩形
菱形
会用数学的眼光观察现实世界!
会用数学的思维思考现实世界!
会用数学的语言表达现实世界!
齐展望
……
谢 谢 大 家 !
汇报人姓名
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
