初中数学浙教版八年级下册第5章 特殊平行四边形 课题学习 格点多边形的面积计算 课件(20张PPT)
文档属性
| 名称 | 初中数学浙教版八年级下册第5章 特殊平行四边形 课题学习 格点多边形的面积计算 课件(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 408.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 09:37:47 | ||
图片预览

文档简介
(共20张PPT)
课题学习:格点多边形的面积计算
概念讲解
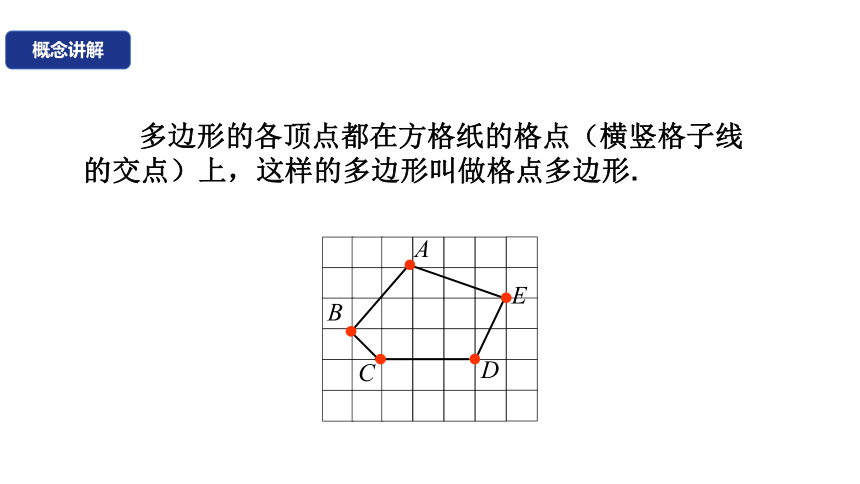
多边形的各顶点都在方格纸的格点(横竖格子线的交点)上,这样的多边形叫做格点多边形.
A
B
C
D
E
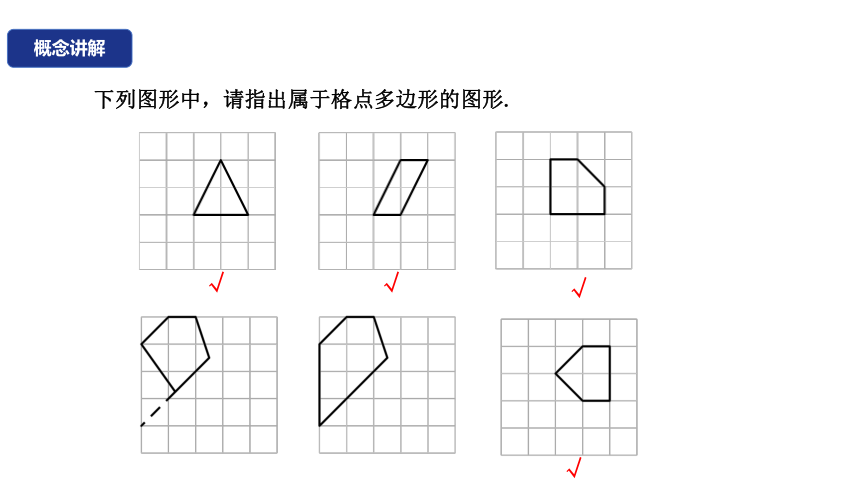
下列图形中,请指出属于格点多边形的图形.
概念讲解
√
√
√
√
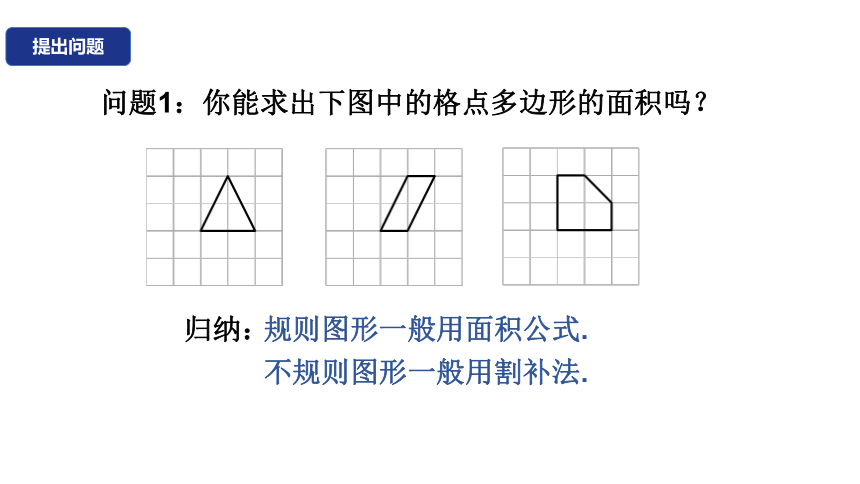
规则图形一般用面积公式.
问题1:你能求出下图中的格点多边形的面积吗?
归纳:
不规则图形一般用割补法.
提出问题
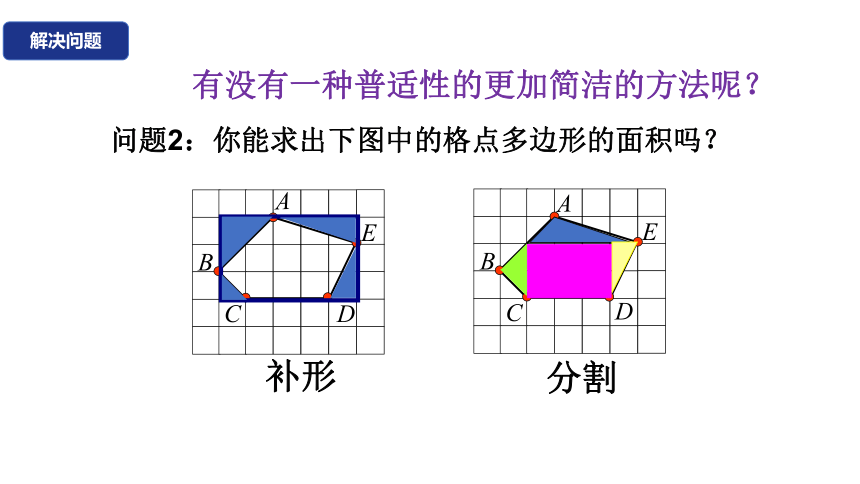
问题2:你能求出下图中的格点多边形的面积吗?
A
B
C
D
E
分割
A
B
C
D
E
补形
有没有一种普适性的更加简洁的方法呢?
解决问题
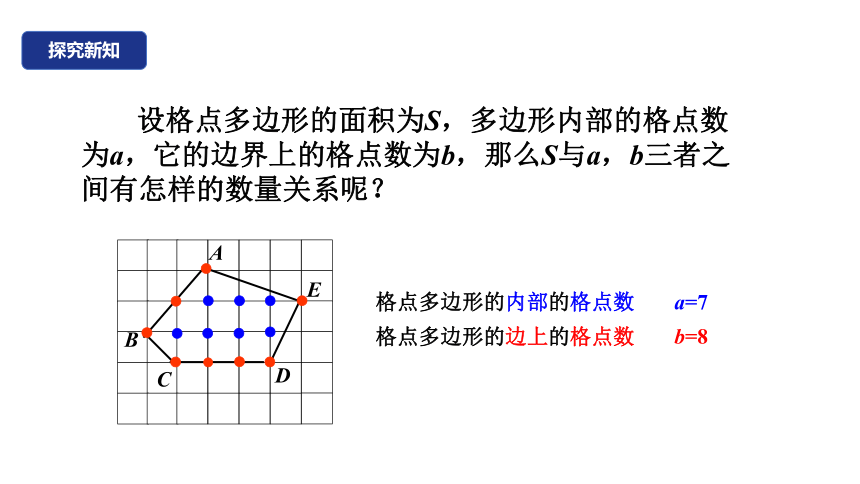
设格点多边形的面积为S,多边形内部的格点数为a,它的边界上的格点数为b,那么S与a,b三者之间有怎样的数量关系呢?
格点多边形的边上的格点数
a=7
格点多边形的内部的格点数
b=8
A
B
C
D
E
探究新知
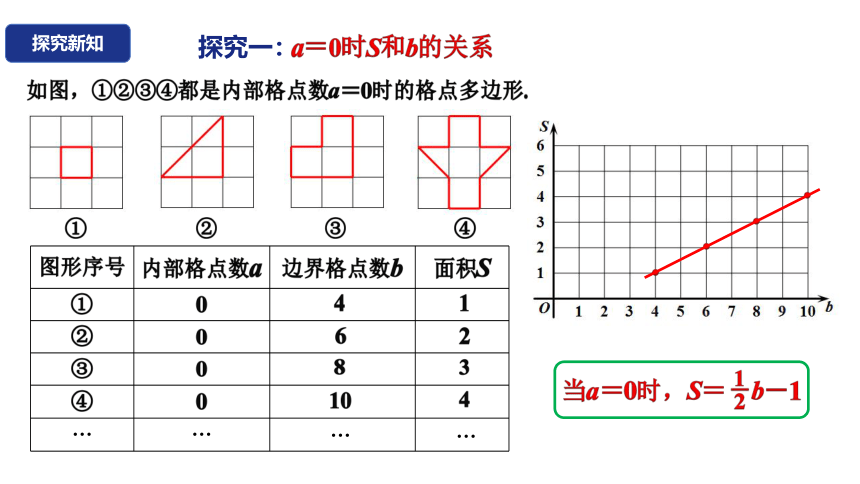
a=0时S和b的关系
如图,①②③④都是内部格点数a=0时的格点多边形.
图形序号 内部格点数a 边界格点数b 面积S
① 0
② 0
③ 0
④ 0
… …
4
6
8
1
2
3
①
②
③
④
10
4
…
…
.
.
.
.
当a=0时,S= b-1
1
2
-
探究一:
探究新知
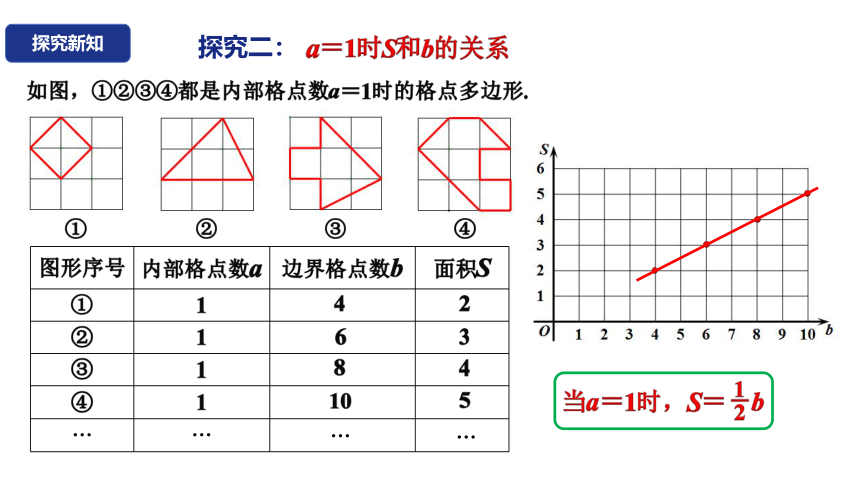
a=1时S和b的关系
如图,①②③④都是内部格点数a=1时的格点多边形.
图形序号 内部格点数a 边界格点数b 面积S
① 1
② 1
③ 1
④ 1
… …
4
6
8
2
3
4
10
5
…
…
.
.
.
.
当a=1时,S= b
1
2
-
①
②
③
④
探究二:
探究新知
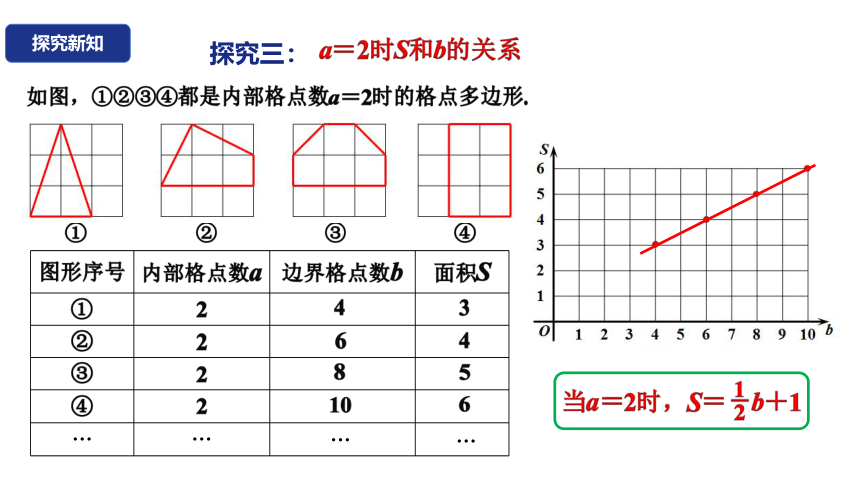
a=2时S和b的关系
如图,①②③④都是内部格点数a=2时的格点多边形.
图形序号 内部格点数a 边界格点数b 面积S
① 2
② 2
③ 2
④ 2
… …
4
6
8
3
4
5
①
②
③
④
10
6
…
…
.
.
.
.
当a=2时,S= b+1
1
2
-
探究新知
探究三:
S和a,b的关系
当a=0时,S= b-1
1
2
-
当a=1时,S= b
1
2
-
当a=2时,S= b+1
1
2
-
当a=1时,S= b+0
1
2
-
当a=a时,S= b+
1
2
-
a-1
格点多边形的面积公式
(皮克定理)
S= 边+内-1
1
2
-
猜想归纳
猜想:
探究二:
探究一:
探究三:
…
…
一般地:
当a=1时,S= b+0
1
2
-
当a=0时,S= b-1
1
2
-
当a=2时,S= b+1
1
2
-
当a=a时,S= b+
1
2
-
a-1
格点多边形的面积公式
(皮克定理)
S= 边+内-1
1
2
-
方法归纳
探究二:
探究一:
探究三:
…
…
一般地:
画图
填表
画图象
判断函数类型
列出关系式
特殊
一般
你将如何验证归纳所得
S=
的正确性?
格点多边形的边上的格点数
a=7
格点多边形的内部的格点数
b=8
A
B
C
D
E
验证猜想
如图所示,在四边形ABCD中,点A,B,C,D均落在单位长度为1的格点图的格点上,要求出四边形ABCD的面积,你有什么方法?
方法1(皮克公式):
该四边形边界上有 个格点,内部有 个格点,所
以根据皮克定理,得
S= ×4+11-1
1
2
-
=12.
4
11
方法2(补全法):
应用新知
如图所示,在四边形ABCD中,点A,B,C,D均落在单位长度为1的格点图的格点上,要求出四边形ABCD的面积,你有什么方法?
方法1(皮克公式):
该四边形边界上有 个格点,内部有 个格点,所
以根据皮克定理,得
S= ×4+11-1
1
2
-
=12.
4
11
方法2(补全法):
S1
S2
S3
S4
S=S长方形-S1-S2-S3-S4 =24-3-6-1-2=12.
应用新知
如图所示,在四边形ABCD中,点A,B,C,D均落在单位长度为1的格点图的格点上,要求出四边形ABCD的面积,你有什么方法?
方法1(皮克定理):
该四边形边界上有 个格点,内部有 个格点,所
以根据皮克定理,得
S= ×4+11-1
1
2
-
=12.
4
11
方法2(补全法):
S=S长方形-S1-S2-S3-S4 =24-3-6-1-2=12.
方法3(切割法):
应用新知
如图所示,在四边形ABCD中,点A,B,C,D均落在单位长度为1的格点图的格点上,要求出四边形ABCD的面积,你有什么方法?
方法1(皮克定理):
该四边形边界上有 个格点,内部有 个格点,所
以根据皮克定理,得
S= ×4+11-1
1
2
-
=12.
4
11
方法2(补全法):
S=S长方形-S1-S2-S3-S4 =24-3-6-1-2=12.
方法3(切割法):
S=S△ACD+S△ACB =4+8=12.
(竖切)
应用新知
如图所示,在四边形ABCD中,点A,B,C,D均落在单位长度为1的格点图的格点上,要求出四边形ABCD的面积,你有什么方法?
方法1(皮克定理):
该四边形边界上有 个格点,内部有 个格点,所
以根据皮克定理,得
S= ×4+11-1
1
2
-
=12.
4
11
方法2(补全法):
S=S长方形-S1-S2-S3-S4 =24-3-6-1-2=12.
方法3(切割法):
S=S△ACD+S△ACB =4+8=12.
(竖切)
S=S△ADB+S△CDB =9+3=12.
(横切)
应用新知
如图所示,已知每个小方格的边长均为1,点A,B,C均在格点上,则点C到AB所在直线的距离等于_________.
解:
连结AC,BC,作CD垂直AB,垂足为点D.
由皮克定理,得
S△ABC= ×4+3-1=4.
1
2
-
易知AB=
S△ABC= AB×CD.
1
2
-
∴CD=
2S△ABC
_______
AB
=
8
____
=
4
_____
5
.
拓展应用
两种方法
一个过程
三种思想
割补法
皮克定理
化归思想
函数思想
建模思想
实验
归纳
猜想
建模
课堂小结
同学们,再见
课题学习:格点多边形的面积计算
概念讲解
多边形的各顶点都在方格纸的格点(横竖格子线的交点)上,这样的多边形叫做格点多边形.
A
B
C
D
E
下列图形中,请指出属于格点多边形的图形.
概念讲解
√
√
√
√
规则图形一般用面积公式.
问题1:你能求出下图中的格点多边形的面积吗?
归纳:
不规则图形一般用割补法.
提出问题
问题2:你能求出下图中的格点多边形的面积吗?
A
B
C
D
E
分割
A
B
C
D
E
补形
有没有一种普适性的更加简洁的方法呢?
解决问题
设格点多边形的面积为S,多边形内部的格点数为a,它的边界上的格点数为b,那么S与a,b三者之间有怎样的数量关系呢?
格点多边形的边上的格点数
a=7
格点多边形的内部的格点数
b=8
A
B
C
D
E
探究新知
a=0时S和b的关系
如图,①②③④都是内部格点数a=0时的格点多边形.
图形序号 内部格点数a 边界格点数b 面积S
① 0
② 0
③ 0
④ 0
… …
4
6
8
1
2
3
①
②
③
④
10
4
…
…
.
.
.
.
当a=0时,S= b-1
1
2
-
探究一:
探究新知
a=1时S和b的关系
如图,①②③④都是内部格点数a=1时的格点多边形.
图形序号 内部格点数a 边界格点数b 面积S
① 1
② 1
③ 1
④ 1
… …
4
6
8
2
3
4
10
5
…
…
.
.
.
.
当a=1时,S= b
1
2
-
①
②
③
④
探究二:
探究新知
a=2时S和b的关系
如图,①②③④都是内部格点数a=2时的格点多边形.
图形序号 内部格点数a 边界格点数b 面积S
① 2
② 2
③ 2
④ 2
… …
4
6
8
3
4
5
①
②
③
④
10
6
…
…
.
.
.
.
当a=2时,S= b+1
1
2
-
探究新知
探究三:
S和a,b的关系
当a=0时,S= b-1
1
2
-
当a=1时,S= b
1
2
-
当a=2时,S= b+1
1
2
-
当a=1时,S= b+0
1
2
-
当a=a时,S= b+
1
2
-
a-1
格点多边形的面积公式
(皮克定理)
S= 边+内-1
1
2
-
猜想归纳
猜想:
探究二:
探究一:
探究三:
…
…
一般地:
当a=1时,S= b+0
1
2
-
当a=0时,S= b-1
1
2
-
当a=2时,S= b+1
1
2
-
当a=a时,S= b+
1
2
-
a-1
格点多边形的面积公式
(皮克定理)
S= 边+内-1
1
2
-
方法归纳
探究二:
探究一:
探究三:
…
…
一般地:
画图
填表
画图象
判断函数类型
列出关系式
特殊
一般
你将如何验证归纳所得
S=
的正确性?
格点多边形的边上的格点数
a=7
格点多边形的内部的格点数
b=8
A
B
C
D
E
验证猜想
如图所示,在四边形ABCD中,点A,B,C,D均落在单位长度为1的格点图的格点上,要求出四边形ABCD的面积,你有什么方法?
方法1(皮克公式):
该四边形边界上有 个格点,内部有 个格点,所
以根据皮克定理,得
S= ×4+11-1
1
2
-
=12.
4
11
方法2(补全法):
应用新知
如图所示,在四边形ABCD中,点A,B,C,D均落在单位长度为1的格点图的格点上,要求出四边形ABCD的面积,你有什么方法?
方法1(皮克公式):
该四边形边界上有 个格点,内部有 个格点,所
以根据皮克定理,得
S= ×4+11-1
1
2
-
=12.
4
11
方法2(补全法):
S1
S2
S3
S4
S=S长方形-S1-S2-S3-S4 =24-3-6-1-2=12.
应用新知
如图所示,在四边形ABCD中,点A,B,C,D均落在单位长度为1的格点图的格点上,要求出四边形ABCD的面积,你有什么方法?
方法1(皮克定理):
该四边形边界上有 个格点,内部有 个格点,所
以根据皮克定理,得
S= ×4+11-1
1
2
-
=12.
4
11
方法2(补全法):
S=S长方形-S1-S2-S3-S4 =24-3-6-1-2=12.
方法3(切割法):
应用新知
如图所示,在四边形ABCD中,点A,B,C,D均落在单位长度为1的格点图的格点上,要求出四边形ABCD的面积,你有什么方法?
方法1(皮克定理):
该四边形边界上有 个格点,内部有 个格点,所
以根据皮克定理,得
S= ×4+11-1
1
2
-
=12.
4
11
方法2(补全法):
S=S长方形-S1-S2-S3-S4 =24-3-6-1-2=12.
方法3(切割法):
S=S△ACD+S△ACB =4+8=12.
(竖切)
应用新知
如图所示,在四边形ABCD中,点A,B,C,D均落在单位长度为1的格点图的格点上,要求出四边形ABCD的面积,你有什么方法?
方法1(皮克定理):
该四边形边界上有 个格点,内部有 个格点,所
以根据皮克定理,得
S= ×4+11-1
1
2
-
=12.
4
11
方法2(补全法):
S=S长方形-S1-S2-S3-S4 =24-3-6-1-2=12.
方法3(切割法):
S=S△ACD+S△ACB =4+8=12.
(竖切)
S=S△ADB+S△CDB =9+3=12.
(横切)
应用新知
如图所示,已知每个小方格的边长均为1,点A,B,C均在格点上,则点C到AB所在直线的距离等于_________.
解:
连结AC,BC,作CD垂直AB,垂足为点D.
由皮克定理,得
S△ABC= ×4+3-1=4.
1
2
-
易知AB=
S△ABC= AB×CD.
1
2
-
∴CD=
2S△ABC
_______
AB
=
8
____
=
4
_____
5
.
拓展应用
两种方法
一个过程
三种思想
割补法
皮克定理
化归思想
函数思想
建模思想
实验
归纳
猜想
建模
课堂小结
同学们,再见
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
