浙教版数学九年级下册1.3 解直角三角形 课件(19张PPT)
文档属性
| 名称 | 浙教版数学九年级下册1.3 解直角三角形 课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-10 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
解直角三角形
单击此处添加副标题
复习回顾
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
∠A+∠B=90°
AC2+BC2=AB2
定义:在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.
解决有关梯形的计算问题
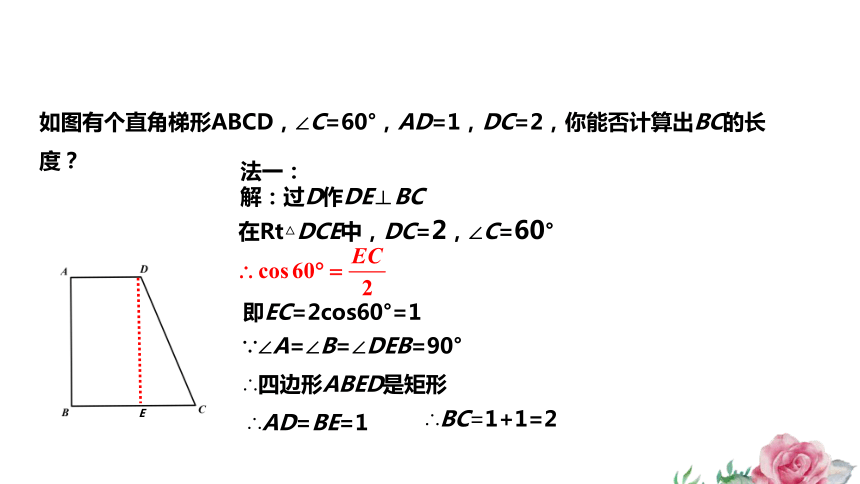
如图有个直角梯形ABCD,∠C=60°,AD=1,DC=2,你能否计算出BC的长度?
E
【分析】1.添加高线,构造直角三角形
2.解直角三角形
如图有个直角梯形ABCD,∠C=60°,AD=1,DC=2,你能否计算出BC的长度?
法一:
解:过D作DE⊥BC
在Rt△DCE中,DC=2,∠C=60°
即EC=2cos60°=1
∵∠A=∠B=∠DEB=90°
∴四边形ABED是矩形
∴AD=BE=1
∴BC=1+1=2
E
E
法二:
解:延长BA,CD,交于点E
∵AD//BC
∴∠C=∠EDA=60°
∵在Rt△EAD中,AD=1
如图有个直角梯形ABCD,∠C=60°,AD=1,DC=2,你能否计算出BC的长度?
∴CE=ED+DC=4
∵在Rt△EBC中,∠C=60°
∴BC=2
【方法】解决这类梯形的计算问题,我们可以通过添加高线化归为解直角三角形问题。
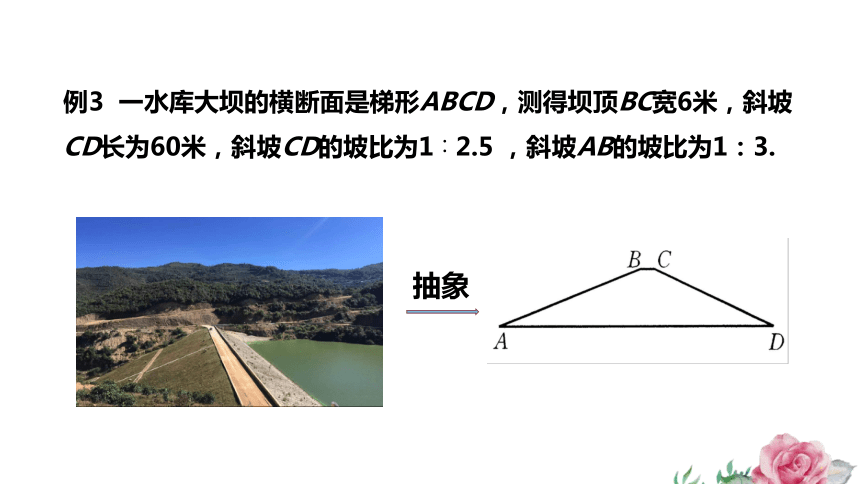
例3 一水库大坝的横断面是梯形ABCD,测得坝顶BC宽6米,斜坡CD长为60米,斜坡CD的坡比为1∶2.5 ,斜坡AB的坡比为1:3.
抽象
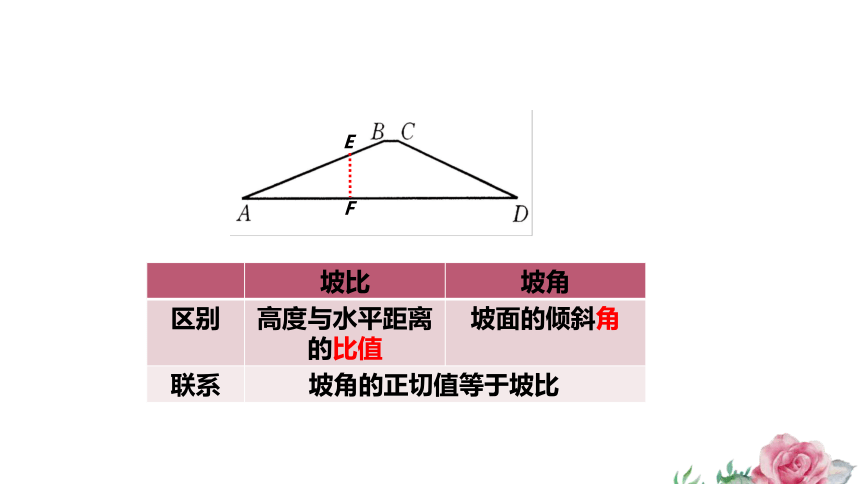
坡比 坡角
区别 高度与水平距离的比值 坡面的倾斜角
联系 E
F
坡角的正切值等于坡比
例3 一水库大坝的横断面是梯形ABCD,测得坝顶BC宽6米,斜坡CD长为60米,斜坡CD的坡比为1∶2.5 ,斜坡AB的坡比为1:3.求:
(1)斜坡CD的坡角∠D与坝底AD的宽度;(角度精确到1′,长度精确到0.1米)
1∶3
1∶2.5
【思考】如何转化问题?
1∶3
E
F
1∶2.5
解:(1)如图,作BE⊥AD,CF⊥AD,点E,F为垂足
在Rt△CFD中,
∴ ∠D≈21°48′.
∴ CF= CD ·sinD=60 × sin 21°48′≈22.28(m)
DF= CD·cosD=60 × cos21°48′≈55.71(m)
∴AD=AE+EF+DF=AE+BC+DF
=66.84+6+55.71=128.55≈128.6 (m)
(1)斜坡CD的坡角∠D与坝底AD的宽度;(角度精确到1′,长度精确到0.1米)
∴ AE=3BE=3CF=66.84(m),
例3 一水库大坝的横断面是梯形ABCD,测得坝顶BC宽6米,斜坡CD长为60米,斜坡CD的坡比为1∶2.5 ,斜坡AB的坡比为1:3.求:
1∶3
1∶2.5
(2)若堤坝长150m,问建造这个堤坝需用多少土石方(精确到1m3).
解:(2)横断面面积:
需要土石方:
体育项目400M栏比赛中,规定相邻两栏架的路程为45m.
在弯道处,以跑道离内侧0.3m处的弧线(图1-17中的虚线)的长度作为相邻两栏架之间的间隔路程.
已知跑道的内侧线半径为36m.在放置好A栏架后,给你皮卷尺,你能否确定B栏架的位置?
解决有关圆形的计算问题
抽象
例4 体育项目400M栏比赛中,规定相邻两栏架的路程为45m.
在弯道处,以跑道离内侧0.3m处的弧线(图1-17中的虚线)的长度作为相邻两栏架之间的间隔路程.
已知跑道的内侧线半径为36m.问在设定A栏架后,B栏架离栏架的距离是多少(π取3.14,结果精确到0.1m)
【分析】1.添加高线,构造直角三角形.
2.利用弧长计算角度
解:如图,连结AB.由题意得 =45m,OB=36.3m
设∠AOB=n°,由弧长公式
可以得到
作OC⊥AB于点C
∵OA=OB,
∴AC=BC, ∠AOC=0.5∠AOB=35.52°
∴ AC=OAsin∠AOC
=36.3×sin 35.52°
≈21.09(m),
∴ AB=2AC=2×21.09≈42.2(m).
答:设定A栏架的位置后,B栏架离A栏架的距离约为42.2m.
【思考】若过点B作BC⊥AO,构造直角三角形,是否可行?
【方法】解决这类圆形的计算问题,我们可以通过添加高线化归为解直角三角形问题。
探究活动
如图,在圆内接正十边形中,AB是正十边形的一条边,M是∠ABO的平分线与半径OA的交点.
(1)设⊙O的半径为R,用关于R的代数式表示正十边形的边长AB.
法一(相似):由题意得∠O=36°,∠OAB=72°
∵BM平分∠OAB
∴∠OBM=∠ABM=36°
∴∠ABM=∠O
∴△ABM∽△BOA
设AB=x,则
∵∠O=∠OBM=36°
∴OM=BM=AB
法二(解直角三角形):
过点O作OC⊥AB
C
BC=AC
∵在Rt△BOC中,BC=OB·sin∠BOC=Rsin18°
∴AB=2BC=2Rsin18°
(2)你发现sin18°和黄金比有怎样的关系?
C
(2)你发现sin18°和黄金比有怎样的关系?
∴sin18°等于黄金比的一半.
【思考】你还能提出什么问题?
课堂小结
实际问题
抽象
转化
模型
抽象
转化
作业
必做题:作业本
选做题:书本作业题6
解直角三角形
单击此处添加副标题
复习回顾
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
∠A+∠B=90°
AC2+BC2=AB2
定义:在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.
解决有关梯形的计算问题
如图有个直角梯形ABCD,∠C=60°,AD=1,DC=2,你能否计算出BC的长度?
E
【分析】1.添加高线,构造直角三角形
2.解直角三角形
如图有个直角梯形ABCD,∠C=60°,AD=1,DC=2,你能否计算出BC的长度?
法一:
解:过D作DE⊥BC
在Rt△DCE中,DC=2,∠C=60°
即EC=2cos60°=1
∵∠A=∠B=∠DEB=90°
∴四边形ABED是矩形
∴AD=BE=1
∴BC=1+1=2
E
E
法二:
解:延长BA,CD,交于点E
∵AD//BC
∴∠C=∠EDA=60°
∵在Rt△EAD中,AD=1
如图有个直角梯形ABCD,∠C=60°,AD=1,DC=2,你能否计算出BC的长度?
∴CE=ED+DC=4
∵在Rt△EBC中,∠C=60°
∴BC=2
【方法】解决这类梯形的计算问题,我们可以通过添加高线化归为解直角三角形问题。
例3 一水库大坝的横断面是梯形ABCD,测得坝顶BC宽6米,斜坡CD长为60米,斜坡CD的坡比为1∶2.5 ,斜坡AB的坡比为1:3.
抽象
坡比 坡角
区别 高度与水平距离的比值 坡面的倾斜角
联系 E
F
坡角的正切值等于坡比
例3 一水库大坝的横断面是梯形ABCD,测得坝顶BC宽6米,斜坡CD长为60米,斜坡CD的坡比为1∶2.5 ,斜坡AB的坡比为1:3.求:
(1)斜坡CD的坡角∠D与坝底AD的宽度;(角度精确到1′,长度精确到0.1米)
1∶3
1∶2.5
【思考】如何转化问题?
1∶3
E
F
1∶2.5
解:(1)如图,作BE⊥AD,CF⊥AD,点E,F为垂足
在Rt△CFD中,
∴ ∠D≈21°48′.
∴ CF= CD ·sinD=60 × sin 21°48′≈22.28(m)
DF= CD·cosD=60 × cos21°48′≈55.71(m)
∴AD=AE+EF+DF=AE+BC+DF
=66.84+6+55.71=128.55≈128.6 (m)
(1)斜坡CD的坡角∠D与坝底AD的宽度;(角度精确到1′,长度精确到0.1米)
∴ AE=3BE=3CF=66.84(m),
例3 一水库大坝的横断面是梯形ABCD,测得坝顶BC宽6米,斜坡CD长为60米,斜坡CD的坡比为1∶2.5 ,斜坡AB的坡比为1:3.求:
1∶3
1∶2.5
(2)若堤坝长150m,问建造这个堤坝需用多少土石方(精确到1m3).
解:(2)横断面面积:
需要土石方:
体育项目400M栏比赛中,规定相邻两栏架的路程为45m.
在弯道处,以跑道离内侧0.3m处的弧线(图1-17中的虚线)的长度作为相邻两栏架之间的间隔路程.
已知跑道的内侧线半径为36m.在放置好A栏架后,给你皮卷尺,你能否确定B栏架的位置?
解决有关圆形的计算问题
抽象
例4 体育项目400M栏比赛中,规定相邻两栏架的路程为45m.
在弯道处,以跑道离内侧0.3m处的弧线(图1-17中的虚线)的长度作为相邻两栏架之间的间隔路程.
已知跑道的内侧线半径为36m.问在设定A栏架后,B栏架离栏架的距离是多少(π取3.14,结果精确到0.1m)
【分析】1.添加高线,构造直角三角形.
2.利用弧长计算角度
解:如图,连结AB.由题意得 =45m,OB=36.3m
设∠AOB=n°,由弧长公式
可以得到
作OC⊥AB于点C
∵OA=OB,
∴AC=BC, ∠AOC=0.5∠AOB=35.52°
∴ AC=OAsin∠AOC
=36.3×sin 35.52°
≈21.09(m),
∴ AB=2AC=2×21.09≈42.2(m).
答:设定A栏架的位置后,B栏架离A栏架的距离约为42.2m.
【思考】若过点B作BC⊥AO,构造直角三角形,是否可行?
【方法】解决这类圆形的计算问题,我们可以通过添加高线化归为解直角三角形问题。
探究活动
如图,在圆内接正十边形中,AB是正十边形的一条边,M是∠ABO的平分线与半径OA的交点.
(1)设⊙O的半径为R,用关于R的代数式表示正十边形的边长AB.
法一(相似):由题意得∠O=36°,∠OAB=72°
∵BM平分∠OAB
∴∠OBM=∠ABM=36°
∴∠ABM=∠O
∴△ABM∽△BOA
设AB=x,则
∵∠O=∠OBM=36°
∴OM=BM=AB
法二(解直角三角形):
过点O作OC⊥AB
C
BC=AC
∵在Rt△BOC中,BC=OB·sin∠BOC=Rsin18°
∴AB=2BC=2Rsin18°
(2)你发现sin18°和黄金比有怎样的关系?
C
(2)你发现sin18°和黄金比有怎样的关系?
∴sin18°等于黄金比的一半.
【思考】你还能提出什么问题?
课堂小结
实际问题
抽象
转化
模型
抽象
转化
作业
必做题:作业本
选做题:书本作业题6
