浙教版数学九年级下册3.3 由三视图描述几何体 课件(17张PPT)
文档属性
| 名称 | 浙教版数学九年级下册3.3 由三视图描述几何体 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-10 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
3.3 由三视图描述几何体
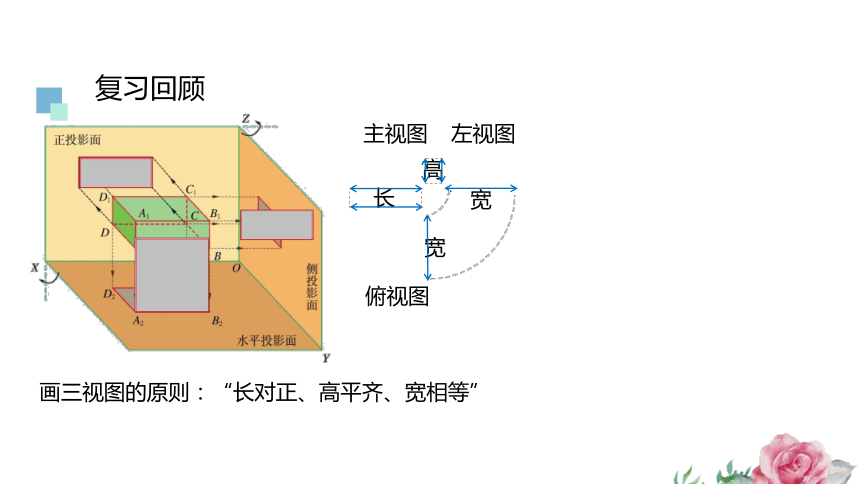
复习回顾
主视图
俯视图
画三视图的原则:“长对正、高平齐、宽相等”
长
宽
宽
高
左视图
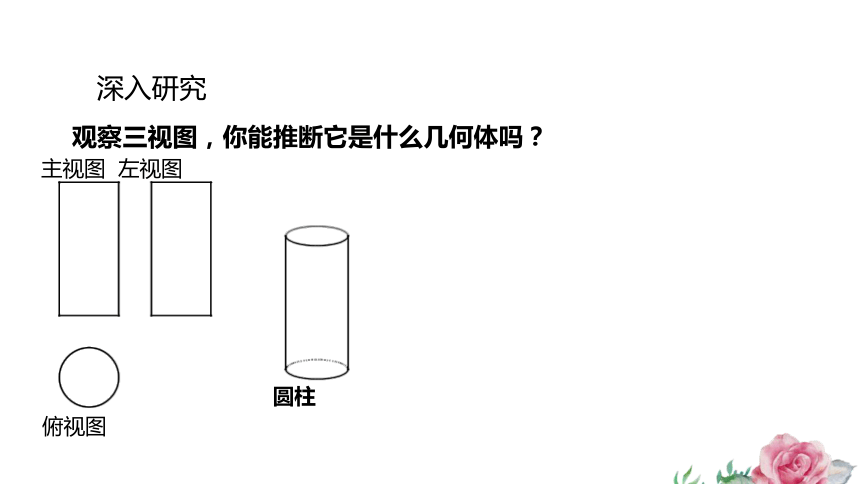
观察三视图,你能推断它是什么几何体吗?
深入研究
主视图 左视图
俯视图
圆柱
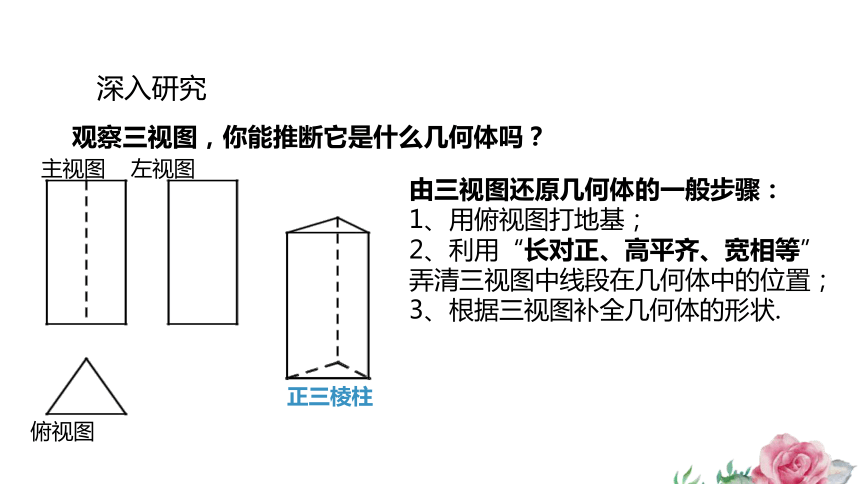
主视图 左视图
俯视图
正三棱柱
深入研究
观察三视图,你能推断它是什么几何体吗?
由三视图还原几何体的一般步骤:
1、用俯视图打地基;
2、利用“长对正、高平齐、宽相等”弄清三视图中线段在几何体中的位置;
3、根据三视图补全几何体的形状.
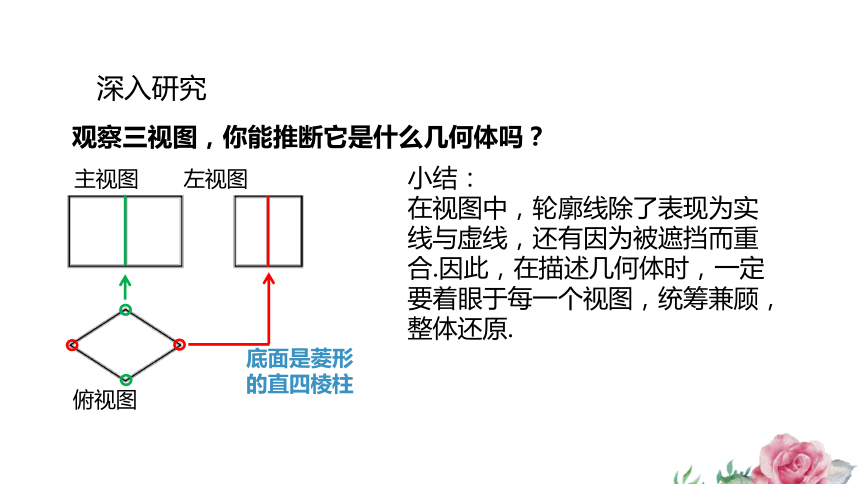
主视图 左视图
俯视图
深入研究
观察三视图,你能推断它是什么几何体吗?
底面是菱形的直四棱柱
小结:
在视图中,轮廓线除了表现为实线与虚线,还有因为被遮挡而重合.因此,在描述几何体时,一定要着眼于每一个视图,统筹兼顾,整体还原.
主视图 左视图
俯视图
深入研究
观察三视图,你能推断它是什么几何体吗?
直五棱柱
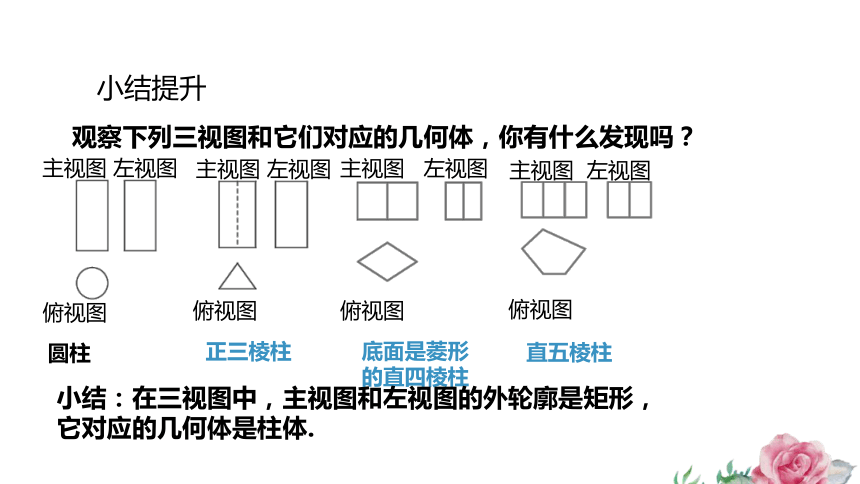
小结提升
观察下列三视图和它们对应的几何体,你有什么发现吗?
直五棱柱
底面是菱形的直四棱柱
主视图 左视图
俯视图
正三棱柱
主视图 左视图
俯视图
主视图 左视图
俯视图
主视图 左视图
俯视图
圆柱
小结:在三视图中,主视图和左视图的外轮廓是矩形,它对应的几何体是柱体.
主视图 左视图
俯视图
横放的正三棱柱
小结:
在三视图中,如果有两个视图的外轮廓是矩形,那它对应的几何体是柱体.
观察三视图,你能推断它是什么几何体吗?
深入研究
主视图 左视图
俯视图
圆锥
观察三视图,你能推断它是什么几何体吗?
深入研究
主视图 左视图
俯视图
正四棱锥
小结:
在三视图中,如果有两个视图的外轮廓是等腰三角形,那它对应的几何体是锥体.
主视图 左视图
俯视图
观察三视图,你能推断它是什么几何体吗?
深入研究
长方体上搁了一个球
小结:
对于组合体,可联系学过的基本几何体进行描述.
主视图 左视图
俯视图
小结:
4
2
3
4
2
4
3
深入研究
观察三视图,你能推断它是什么几何体吗?
主视图的每列正方形个数
左视图的每列正方形个数
俯视图对应行上搭的小立方块最高的块数
俯视图对应列上搭的小立方块最高的块数
俯视图对应列上搭的小立方块最高的块数
由几个相同的小立方块搭成的几何体的俯视图如图所示,方格中的数字表示在该位置的小立方块的个数.请画出这个几何体的三视图.
3
4
1
2
主视图 左视图
俯视图
深入研究
主视图的每列正方形个数
左视图的每列正方形个数
俯视图对应行上搭的小立方块最高的块数
1
主视图 左视图
俯视图
底面是直角梯形的直四棱柱
已知一个几何体的三视图如图所示,描述该几何体的形状,量出三视图的有关尺寸,并根据已知的比例求出它的侧面积.
例题解析
比例:1:3
思考:
1、要计算该四棱柱的侧面积,需要量出哪些线段的长度?
2、为减少误差,能少量几条线段吗?
1
1.5cm
3cm
1.5
1cm
2cm
根据比例1:3,可得这个直四棱柱各个方
向的尺寸如图所示.
主视图 左视图
俯视图
底面是直角梯形的直四棱柱
已知一个几何体的三视图如图所示,描述该几何体的形状,量出三视图的有关尺寸,并根据已知的比例求出它的侧面积.
例题解析
比例:1:3
思考:还有其他方法计算该直棱柱的侧面积吗?
方法二:
方法一:
1
1.5cm
3cm
1.5
1cm
1
2cm
底面周长
底面是直角梯形的直四棱柱
已知一个几何体的三视图如图所示,描述该几何体的形状,量出三视图的有关尺寸,并根据已知的比例求出它的侧面积.
例题解析
思考:还有其他方法计算该直棱柱的侧面积吗?
方法二:
方法一:
直棱柱相关公式:
底面周长
课堂小结
2 根据三视图计算几何体的侧面积等
1 由三视图还原几何体形状
1)三视图中有两个视图的外轮廓为矩形,则它对应的几何体是柱体;有两个视图的外轮廓为等腰三角形,则它对应的几何体是锥体.
2)对于组合体,可联系学过的基本几何体进行描述.
3)对于小立方块组合体,可利用两个等式.
关键:利用 “长对正、高平齐、宽相等”找到三视图中对应线段,量出尺寸后,根据比例,计算实际尺寸,利用公式计算几何体的侧面积等.
同学们,再见!
单击此处添加副标题
3.3 由三视图描述几何体
复习回顾
主视图
俯视图
画三视图的原则:“长对正、高平齐、宽相等”
长
宽
宽
高
左视图
观察三视图,你能推断它是什么几何体吗?
深入研究
主视图 左视图
俯视图
圆柱
主视图 左视图
俯视图
正三棱柱
深入研究
观察三视图,你能推断它是什么几何体吗?
由三视图还原几何体的一般步骤:
1、用俯视图打地基;
2、利用“长对正、高平齐、宽相等”弄清三视图中线段在几何体中的位置;
3、根据三视图补全几何体的形状.
主视图 左视图
俯视图
深入研究
观察三视图,你能推断它是什么几何体吗?
底面是菱形的直四棱柱
小结:
在视图中,轮廓线除了表现为实线与虚线,还有因为被遮挡而重合.因此,在描述几何体时,一定要着眼于每一个视图,统筹兼顾,整体还原.
主视图 左视图
俯视图
深入研究
观察三视图,你能推断它是什么几何体吗?
直五棱柱
小结提升
观察下列三视图和它们对应的几何体,你有什么发现吗?
直五棱柱
底面是菱形的直四棱柱
主视图 左视图
俯视图
正三棱柱
主视图 左视图
俯视图
主视图 左视图
俯视图
主视图 左视图
俯视图
圆柱
小结:在三视图中,主视图和左视图的外轮廓是矩形,它对应的几何体是柱体.
主视图 左视图
俯视图
横放的正三棱柱
小结:
在三视图中,如果有两个视图的外轮廓是矩形,那它对应的几何体是柱体.
观察三视图,你能推断它是什么几何体吗?
深入研究
主视图 左视图
俯视图
圆锥
观察三视图,你能推断它是什么几何体吗?
深入研究
主视图 左视图
俯视图
正四棱锥
小结:
在三视图中,如果有两个视图的外轮廓是等腰三角形,那它对应的几何体是锥体.
主视图 左视图
俯视图
观察三视图,你能推断它是什么几何体吗?
深入研究
长方体上搁了一个球
小结:
对于组合体,可联系学过的基本几何体进行描述.
主视图 左视图
俯视图
小结:
4
2
3
4
2
4
3
深入研究
观察三视图,你能推断它是什么几何体吗?
主视图的每列正方形个数
左视图的每列正方形个数
俯视图对应行上搭的小立方块最高的块数
俯视图对应列上搭的小立方块最高的块数
俯视图对应列上搭的小立方块最高的块数
由几个相同的小立方块搭成的几何体的俯视图如图所示,方格中的数字表示在该位置的小立方块的个数.请画出这个几何体的三视图.
3
4
1
2
主视图 左视图
俯视图
深入研究
主视图的每列正方形个数
左视图的每列正方形个数
俯视图对应行上搭的小立方块最高的块数
1
主视图 左视图
俯视图
底面是直角梯形的直四棱柱
已知一个几何体的三视图如图所示,描述该几何体的形状,量出三视图的有关尺寸,并根据已知的比例求出它的侧面积.
例题解析
比例:1:3
思考:
1、要计算该四棱柱的侧面积,需要量出哪些线段的长度?
2、为减少误差,能少量几条线段吗?
1
1.5cm
3cm
1.5
1cm
2cm
根据比例1:3,可得这个直四棱柱各个方
向的尺寸如图所示.
主视图 左视图
俯视图
底面是直角梯形的直四棱柱
已知一个几何体的三视图如图所示,描述该几何体的形状,量出三视图的有关尺寸,并根据已知的比例求出它的侧面积.
例题解析
比例:1:3
思考:还有其他方法计算该直棱柱的侧面积吗?
方法二:
方法一:
1
1.5cm
3cm
1.5
1cm
1
2cm
底面周长
底面是直角梯形的直四棱柱
已知一个几何体的三视图如图所示,描述该几何体的形状,量出三视图的有关尺寸,并根据已知的比例求出它的侧面积.
例题解析
思考:还有其他方法计算该直棱柱的侧面积吗?
方法二:
方法一:
直棱柱相关公式:
底面周长
课堂小结
2 根据三视图计算几何体的侧面积等
1 由三视图还原几何体形状
1)三视图中有两个视图的外轮廓为矩形,则它对应的几何体是柱体;有两个视图的外轮廓为等腰三角形,则它对应的几何体是锥体.
2)对于组合体,可联系学过的基本几何体进行描述.
3)对于小立方块组合体,可利用两个等式.
关键:利用 “长对正、高平齐、宽相等”找到三视图中对应线段,量出尺寸后,根据比例,计算实际尺寸,利用公式计算几何体的侧面积等.
同学们,再见!
单击此处添加副标题
