浙教版数学九年级下册第二章 直线与圆的位置关系 小结课件(23张PPT)
文档属性
| 名称 | 浙教版数学九年级下册第二章 直线与圆的位置关系 小结课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 571.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-10 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
直线与圆的位置关系(小结)
年 级:九年级
学 科:初中数学(浙教版)
回忆知识
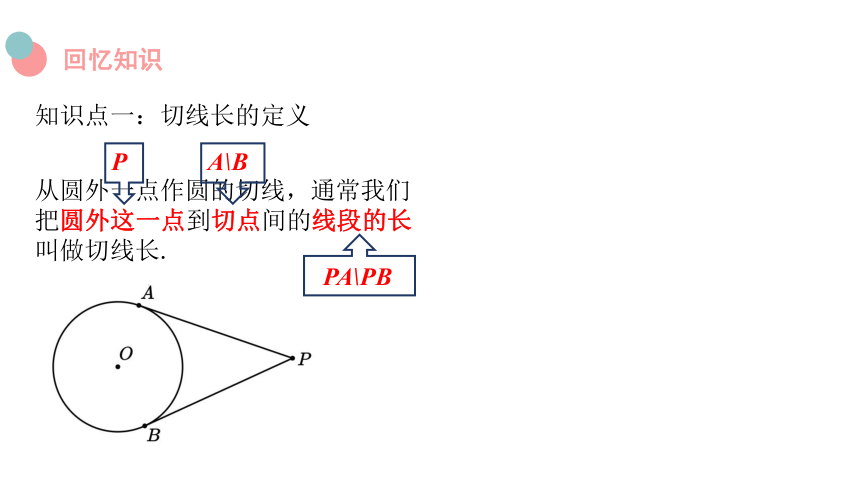
知识点一:切线长的定义
从圆外一点作圆的切线,通常我们把圆外这一点到切点间的线段的长叫做切线长.
P
A\B
PA\PB
回忆知识
知识点二:切线长定理
过圆外一点所做的圆的两条切线长相等.
几何语言:
∵的切线,
∴
回忆知识
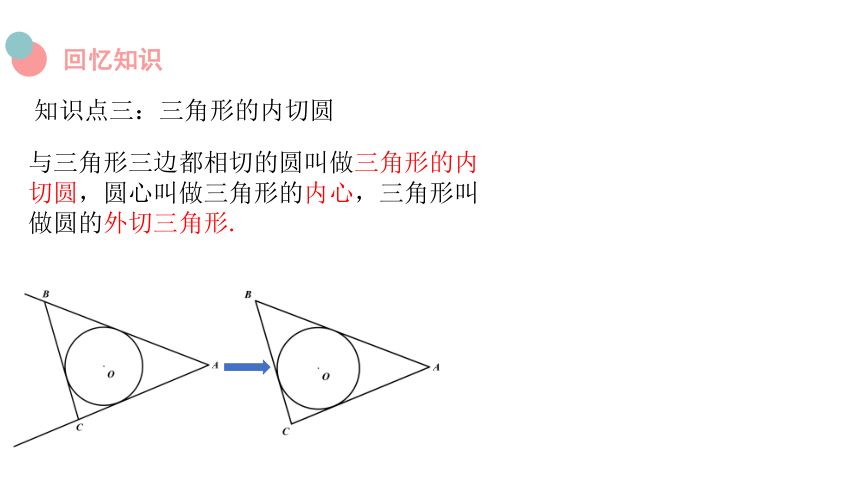
知识点三:三角形的内切圆
与三角形三边都相切的圆叫做三角形的内切圆,圆心叫做三角形的内心,三角形叫做圆的外切三角形.
回忆知识
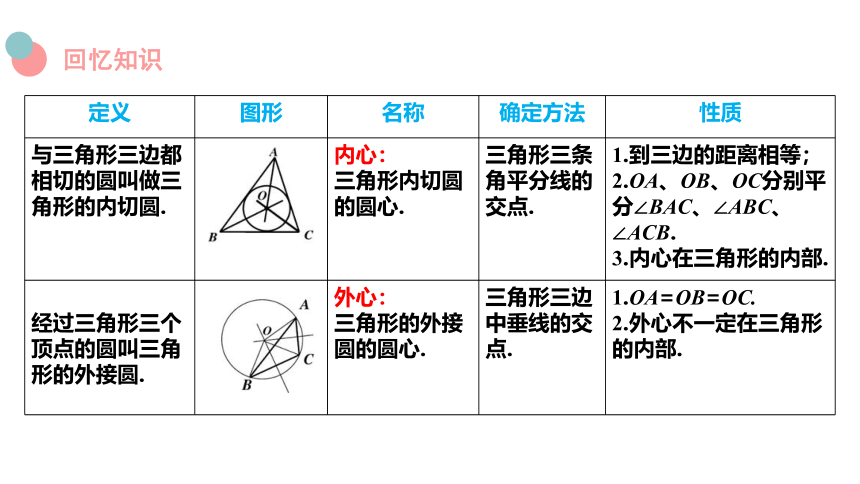
定义 图形 名称 确定方法 性质
与三角形三边都相切的圆叫做三角形的内切圆. 内心: 三角形内切圆的圆心. 三角形三条角平分线的交点. 1.到三边的距离相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB.
3.内心在三角形的内部.
经过三角形三个顶点的圆叫三角形的外接圆. 外心: 三角形的外接圆的圆心. 三角形三边中垂线的交点. 1.OA=OB=OC.
2.外心不一定在三角形的内部.
回忆知识
基础巩固
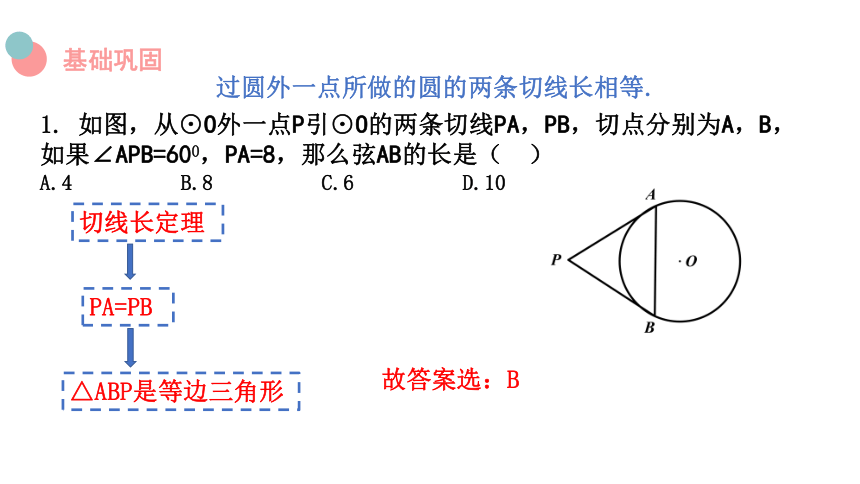
1. 如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B,如果∠APB=600,PA=8,那么弦AB的长是( )
A.4 B.8 C.6 D.10
切线长定理
PA=PB
△ABP是等边三角形
故答案选:B
过圆外一点所做的圆的两条切线长相等.
基础巩固
基础巩固
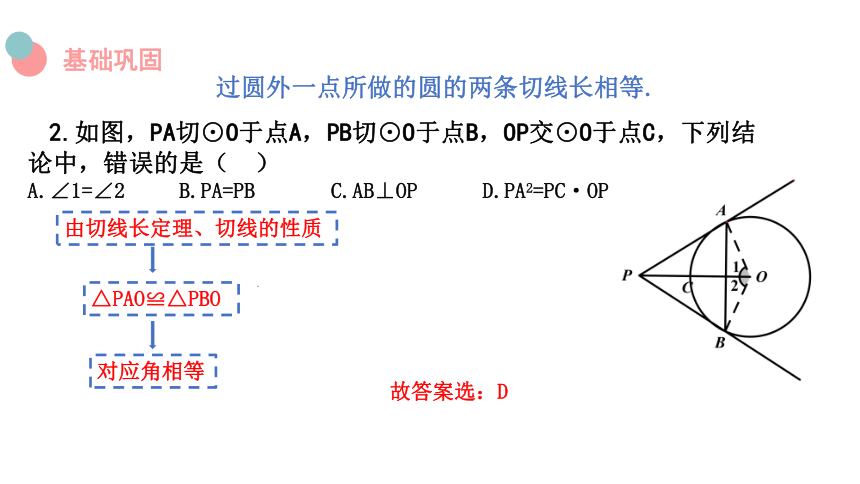
过圆外一点所做的圆的两条切线长相等.
2.如图,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中,错误的是( )
A.∠1=∠2 B.PA=PB C.AB⊥OP D.PA2=PC·OP
由切线长定理、切线的性质
△PAO≌△PBO
对应角相等
故答案选:D
基础巩固
归纳 切线长定理的基本图形
如图, 是的切线,此图形中含有:
(1)两个等腰三角形,两个直角三角形
(2)一条特殊的角平分线
(3)三个垂直关系
(4)两对互补的角
归纳小结
基础巩
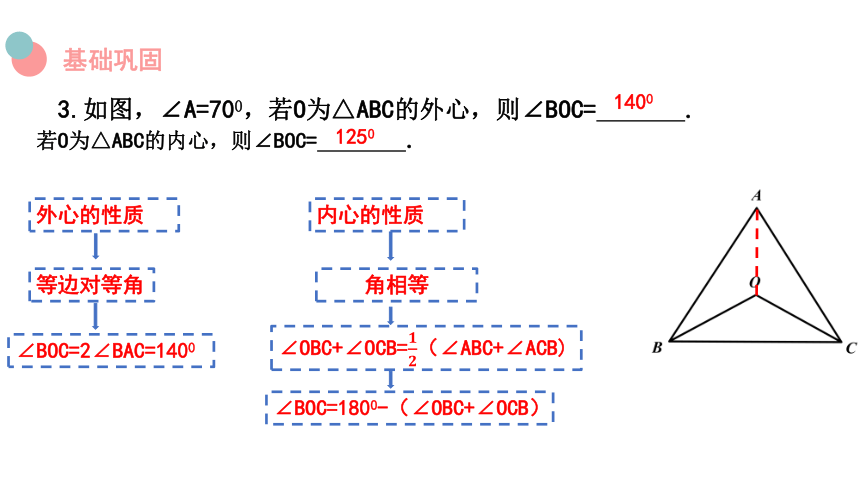
3.如图,∠A=700,若O为△ABC的外心,则∠BOC= .
若O为△ABC的内心,则∠BOC= .
外心的性质
等边对等角
∠BOC=2∠BAC=1400
内心的性质
角相等
∠OBC+∠OCB=(∠ABC+∠ACB)
∠BOC=1800-(∠OBC+∠OCB)
1400
1250
基础巩固
4.如图,一圆外切四边形ABCD,且AB=16,CD=10,则四边形的周长为( )
A.50 B.52 C.54 D.56
四边形的周长=2(AB+CD)=2×26=52
故答案选:B
基础巩固
基础巩固
5.如图,在Rt△ABC中,AC=3,AB=5,圆心O在BC边上,且⊙O与边BC相交于点C和E,与边AB相切于点D,求BD以及BE的长。
由切线长定理
求得线段AD、BD
由切线的性质
得垂直,证得三角形相似
基础巩固
5.如图,在Rt△ABC中,AC=3,AB=5,圆心O在BC边上,且⊙O与边BC相交于点C和E,与边AB相切于点D,求BD以及BE的长。
解:连接OD
由题意可知AC⊥CE且CE为⊙O的直径
∴AC为⊙O的切线.
又∵AB为⊙O的切线
∴AC=AD=3
∴BD=AB-AD=5-3=2
由切线的性质可知:OD⊥AB
∴∠C=∠ODB=900
又∵∠B=∠B
∴△BDO∽△BCA
∴
由勾股定理得BC=4
∴
∴OD=
BE=BC-CE=4-3=1
基础巩固
基础巩固
6.如图,△ABC的三边分别切⊙O于点D,E,F.若AB=7,AC=8,BC=9,则BE= ,CF= .
4
5
基础巩固
基础巩固
7.如图,在Rt△ABC中,∠C=900,△ABC的内切圆⊙O切AB于点D,切BC于点E ,切AC于点F,AD=4,BD=6,求⊙O的半径,以及Rt△ABC的面积.
由切线长定理
线段相等
切线的性质
正方形
分析:
基础巩固
7.如图,在Rt△ABC中,∠C=900,△ABC的内切圆⊙O切AB于点D,切BC于点E ,切AC于点F,AD=4,BD=6,求⊙O的半径,以及Rt△ABC的面积.
解:连接OD、OE、OF
∵⊙O是△ABC的内切圆,由切线长定理可得
AF=AD=4、BD=BE=6、CE=CF
由切线的性质可得OF⊥AC、OE⊥BC
∵∠C=900
∴四边形CEOF是正方形
设⊙O的半径为,则CF=CE=
在Rt△ABC中,AC2+BC2=AB2
∴
解的
基础巩固
基础巩固
7.如图,在Rt△ABC中,∠C=900,△ABC的内切圆⊙O切AB于点D,切BC于点E ,切AC于点F,AD=4,BD=6,求⊙O的半径,以及Rt△ABC的面积.
半径的第二种求法:
基础巩固
基础巩固
7.如图,在Rt△ABC中,∠C=900,△ABC的内切圆⊙O切AB于点D,切BC于点E ,切AC于点F,AD=4,BD=6,求⊙O的半径,以及Rt△ABC的面积.
Rt△ABC面积的第二种求法:
连接AO、BO、CO
S△ABC=S△ACO+S△BCO+S△ABO
=
=
=24
∴AC=6、BC=8
∴S△ABC=
基础巩固
归纳:
(只针对于直角三角形)
(任意三角形都适用)
归纳小结
8.如图,AB为半圆O的直径,在AB的同侧作AC,BD切半圆O于点A,B,CD切半圆O于点E,若AC=4,BD=9.求⊙O的半径.
F
由切线长定理
AC=CE、DE=DB
勾股定理即可求得半径
分析
拓展提升
8.如图,AB为半圆O的直径,在AB的同侧作AC,BD切半圆O于点A,B,CD切半圆O于点E,若AC=4,BD=9.求⊙O的半径.
F
解:过点C作CF⊥BD于点F
由切线长定理可得
AC=CE=4、DE=DB=9
∴CD=4+9=13
由切线的性质可得
AC⊥AB、BD⊥AB
又∵CF⊥BD
∴四边形ACFB为矩形
∴BF=AC=4
∴DF=BD-BF=5
在Rt△CFD中
CF2+DF2=CD2
解得 CF=12
∴⊙O的半径为6.
拓展提升
圆的切线
切线的判定与性质
切线长的概念
切线长定理
三角形的内切圆定义
三角形的内切圆性质
三角形的内切圆运用
反思小结
9.如图,在Rt△ABC中,AC=3, BC=4,⊙O与△ABC中AB,AC的延长线以及边BC相切,切点分别是D,E,F.
(1)求⊙O的半径以及AD的长.
(2)若∠A=500.求∠O的度数.
课后练习
10.如图,⊙O是Rt△ABC的内切圆,∠C=900,AO的延长线交BC于点D,若AC=4,CD=1,求⊙O的半径.
课后练习
直线与圆的位置关系(小结)
年 级:九年级
学 科:初中数学(浙教版)
回忆知识
知识点一:切线长的定义
从圆外一点作圆的切线,通常我们把圆外这一点到切点间的线段的长叫做切线长.
P
A\B
PA\PB
回忆知识
知识点二:切线长定理
过圆外一点所做的圆的两条切线长相等.
几何语言:
∵的切线,
∴
回忆知识
知识点三:三角形的内切圆
与三角形三边都相切的圆叫做三角形的内切圆,圆心叫做三角形的内心,三角形叫做圆的外切三角形.
回忆知识
定义 图形 名称 确定方法 性质
与三角形三边都相切的圆叫做三角形的内切圆. 内心: 三角形内切圆的圆心. 三角形三条角平分线的交点. 1.到三边的距离相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB.
3.内心在三角形的内部.
经过三角形三个顶点的圆叫三角形的外接圆. 外心: 三角形的外接圆的圆心. 三角形三边中垂线的交点. 1.OA=OB=OC.
2.外心不一定在三角形的内部.
回忆知识
基础巩固
1. 如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B,如果∠APB=600,PA=8,那么弦AB的长是( )
A.4 B.8 C.6 D.10
切线长定理
PA=PB
△ABP是等边三角形
故答案选:B
过圆外一点所做的圆的两条切线长相等.
基础巩固
基础巩固
过圆外一点所做的圆的两条切线长相等.
2.如图,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中,错误的是( )
A.∠1=∠2 B.PA=PB C.AB⊥OP D.PA2=PC·OP
由切线长定理、切线的性质
△PAO≌△PBO
对应角相等
故答案选:D
基础巩固
归纳 切线长定理的基本图形
如图, 是的切线,此图形中含有:
(1)两个等腰三角形,两个直角三角形
(2)一条特殊的角平分线
(3)三个垂直关系
(4)两对互补的角
归纳小结
基础巩
3.如图,∠A=700,若O为△ABC的外心,则∠BOC= .
若O为△ABC的内心,则∠BOC= .
外心的性质
等边对等角
∠BOC=2∠BAC=1400
内心的性质
角相等
∠OBC+∠OCB=(∠ABC+∠ACB)
∠BOC=1800-(∠OBC+∠OCB)
1400
1250
基础巩固
4.如图,一圆外切四边形ABCD,且AB=16,CD=10,则四边形的周长为( )
A.50 B.52 C.54 D.56
四边形的周长=2(AB+CD)=2×26=52
故答案选:B
基础巩固
基础巩固
5.如图,在Rt△ABC中,AC=3,AB=5,圆心O在BC边上,且⊙O与边BC相交于点C和E,与边AB相切于点D,求BD以及BE的长。
由切线长定理
求得线段AD、BD
由切线的性质
得垂直,证得三角形相似
基础巩固
5.如图,在Rt△ABC中,AC=3,AB=5,圆心O在BC边上,且⊙O与边BC相交于点C和E,与边AB相切于点D,求BD以及BE的长。
解:连接OD
由题意可知AC⊥CE且CE为⊙O的直径
∴AC为⊙O的切线.
又∵AB为⊙O的切线
∴AC=AD=3
∴BD=AB-AD=5-3=2
由切线的性质可知:OD⊥AB
∴∠C=∠ODB=900
又∵∠B=∠B
∴△BDO∽△BCA
∴
由勾股定理得BC=4
∴
∴OD=
BE=BC-CE=4-3=1
基础巩固
基础巩固
6.如图,△ABC的三边分别切⊙O于点D,E,F.若AB=7,AC=8,BC=9,则BE= ,CF= .
4
5
基础巩固
基础巩固
7.如图,在Rt△ABC中,∠C=900,△ABC的内切圆⊙O切AB于点D,切BC于点E ,切AC于点F,AD=4,BD=6,求⊙O的半径,以及Rt△ABC的面积.
由切线长定理
线段相等
切线的性质
正方形
分析:
基础巩固
7.如图,在Rt△ABC中,∠C=900,△ABC的内切圆⊙O切AB于点D,切BC于点E ,切AC于点F,AD=4,BD=6,求⊙O的半径,以及Rt△ABC的面积.
解:连接OD、OE、OF
∵⊙O是△ABC的内切圆,由切线长定理可得
AF=AD=4、BD=BE=6、CE=CF
由切线的性质可得OF⊥AC、OE⊥BC
∵∠C=900
∴四边形CEOF是正方形
设⊙O的半径为,则CF=CE=
在Rt△ABC中,AC2+BC2=AB2
∴
解的
基础巩固
基础巩固
7.如图,在Rt△ABC中,∠C=900,△ABC的内切圆⊙O切AB于点D,切BC于点E ,切AC于点F,AD=4,BD=6,求⊙O的半径,以及Rt△ABC的面积.
半径的第二种求法:
基础巩固
基础巩固
7.如图,在Rt△ABC中,∠C=900,△ABC的内切圆⊙O切AB于点D,切BC于点E ,切AC于点F,AD=4,BD=6,求⊙O的半径,以及Rt△ABC的面积.
Rt△ABC面积的第二种求法:
连接AO、BO、CO
S△ABC=S△ACO+S△BCO+S△ABO
=
=
=24
∴AC=6、BC=8
∴S△ABC=
基础巩固
归纳:
(只针对于直角三角形)
(任意三角形都适用)
归纳小结
8.如图,AB为半圆O的直径,在AB的同侧作AC,BD切半圆O于点A,B,CD切半圆O于点E,若AC=4,BD=9.求⊙O的半径.
F
由切线长定理
AC=CE、DE=DB
勾股定理即可求得半径
分析
拓展提升
8.如图,AB为半圆O的直径,在AB的同侧作AC,BD切半圆O于点A,B,CD切半圆O于点E,若AC=4,BD=9.求⊙O的半径.
F
解:过点C作CF⊥BD于点F
由切线长定理可得
AC=CE=4、DE=DB=9
∴CD=4+9=13
由切线的性质可得
AC⊥AB、BD⊥AB
又∵CF⊥BD
∴四边形ACFB为矩形
∴BF=AC=4
∴DF=BD-BF=5
在Rt△CFD中
CF2+DF2=CD2
解得 CF=12
∴⊙O的半径为6.
拓展提升
圆的切线
切线的判定与性质
切线长的概念
切线长定理
三角形的内切圆定义
三角形的内切圆性质
三角形的内切圆运用
反思小结
9.如图,在Rt△ABC中,AC=3, BC=4,⊙O与△ABC中AB,AC的延长线以及边BC相切,切点分别是D,E,F.
(1)求⊙O的半径以及AD的长.
(2)若∠A=500.求∠O的度数.
课后练习
10.如图,⊙O是Rt△ABC的内切圆,∠C=900,AO的延长线交BC于点D,若AC=4,CD=1,求⊙O的半径.
课后练习
