2.6探索勾股定理（2）

课件16张PPT。 2.6探索勾股定理（2） 合作学习： 一、要求每组画一个三角形,使其三边长分别为: （1）3cm, 4cm, 5cm；（2）5cm, 12cm,13cm；
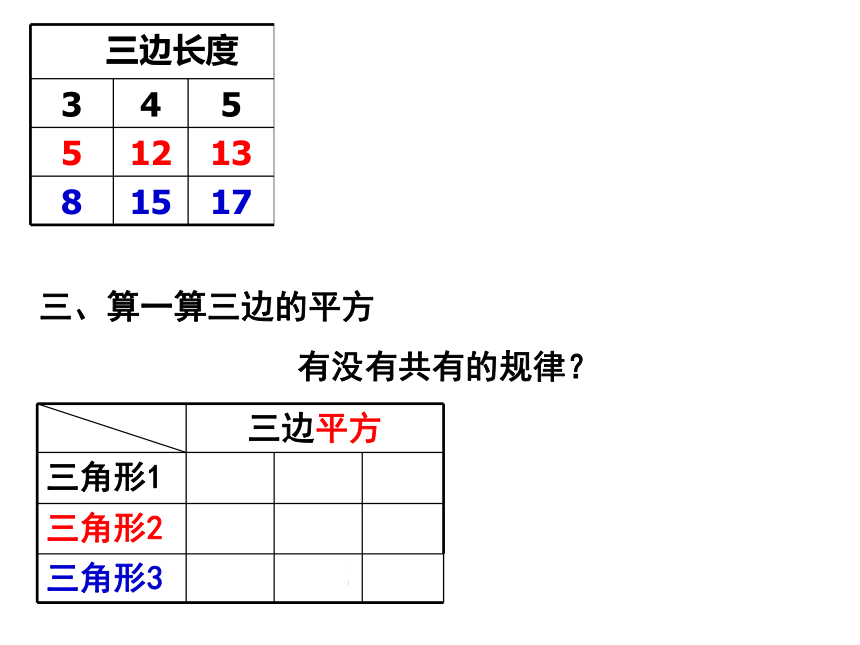
（3）6cm, 8cm, 10cm； 二、再用量角器量一量最大的角，并判断它们是否哪类三角形。直角三角形 三、算一算三边的平方
有没有共有的规律？ 如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形. 即如果三角形的三边长a，b，c有关系 那么这个三角形是直角三角形.结论：如何确定直角的位置呢？ 像3,4,5,这样能够成为直角三角形三条边长的三个正整数，称为勾股数. 分析：根据直角三角形的判定方法, 判断一个三角形是不是直角三角形, 只要看两条较小边长的平方和是否等于最大边长的平方. 例1、判断由线段a，b，c组成的三角形是不是直角
三角形?
(1) a=15，b=17，c=8; (2) a=13，b=15，c=14 解:(1)最大边为17 ∵152+82=225+64 =289172 =289 ∴152+82 =172 ∴以15, 8, 17为边长的三角形是直角三角形 (2)最大边为15 ∵132+142=169+196=365152 =225 ∴132+ 142 ≠ 152 ∴以13, 15, 14为边长的三角形不是直角三角形 练习：下面以a,b,c为边长且所对角分别为∠A ∠B ，∠C的三角形是不是直角三角形？如果是那么哪一个角是直角？（3）变式：a=5n, b=12n, c=13n; (1) a=2 b=1 c= ；　____ _______;是∠ A=90° (2) a=5，b=12，c=13;____ _______;是∠ Ｃ=90° 利用勾股定理的逆定理，先区分最长边与较短两边，然后再比较较短两边的平方和与最长边的平方，若相等，则三角形是直角三角形，并且最长边所对的角是直角，否则该三角形不是直角三角形.1、根据下列条件，判断下面以a、b、
　c 为边的三角形是不是直角三角形?
1、　a=5，b=7，c=8
2、　
3、a : b : c = 3 : 4 : 5 Let me try!4、△ABC的两边AB=5,AC=12,则BC=13 ( ) ??5、在△ABC中,若AC2=BC2-AB2,则∠B=90°( )
快判速断：6、如图在△ABC中AB=4,BC=2,BD=1,CD=
判断下列结论是否正确，并说明理由
(1) CD ⊥AB;
解(1)∵BC2=BD2 +CD2=4(2)∵AC2=AD2+CD2=12∴∠CDB=90°∴CD⊥ABAC2+BC2=16=AB2∴∠ACB=90°∴AC⊥BC(2) AC⊥BC例2、 已知△ABC三条边长分别为a, b, c,且a＝m2－n2，b＝2mn，c＝m2＋n2(m>n，m, n是正整数)。△ABC是直角三角形吗？请说明理由.解：∵ a=m2－n2，b=2mn，c＝m2＋n2∴a2+b2=(m2－n2)2+(2mn)2＝m4－2m2n2＋n4＋4m2n2＝(m2＋n2)2＝m4＋2m2n2＋n4＝c2∴△ABC是直角三角形问：哪边是最长边？你有办法判断吗？1、如图，四边形ABCD中，AB＝3，BC=4,CD=12,AD=13, ∠B=90°，求四边形ABCD的面积.┐拓展提高：解：连结AC，在Rt△ABC中∴S四边形ABCD=S△ABC+S△ACD5 变式：若零件的形状及边长如图（2）所示,你还能求面积吗?图(2) 归纳小结复习勾股定理：
直角三角形两直角边的平方和等于斜边的平方．如果三角形两边的平方和等于第三边平方,
那么这个三角形是直角三角形.今天学习的是勾股定理的逆定理：如果 那么 布置作业1、《作业本》2.6（2）
2、《同步练习》
反馈练习： 1、三角形ABC中,∠A.∠B.∠C.的对边分别是a，b，c,且 c＋a=2b, c – a= b,试问三角形ABC的形状。2: 已知△ABC中,三条边长分别是 、 、 ,
( ＞1),那
么△ABC是直角三角形吗？请说明理由.是直角三角形吗？ 合作探究： 如下图中分别以 三边a,b,c为边向外作正方形，正三角形，为直径作半圆，若S1+S2=S3成立，则