1.1认识三角形 课件(共74张PPT)数学浙教版八年级上册
文档属性
| 名称 | 1.1认识三角形 课件(共74张PPT)数学浙教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-13 19:35:52 | ||
图片预览

文档简介
(共74张PPT)
认识三角形
生活中的三角形
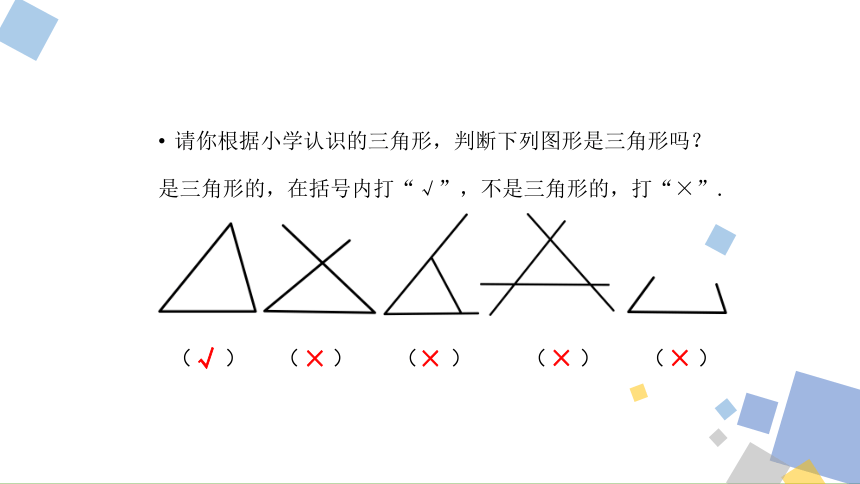
请你根据小学认识的三角形,判断下列图形是三角形吗?
是三角形的,在括号内打“√”,不是三角形的,打“×”.
( ) ( ) ( ) ( ) ( )
√
×
×
×
×
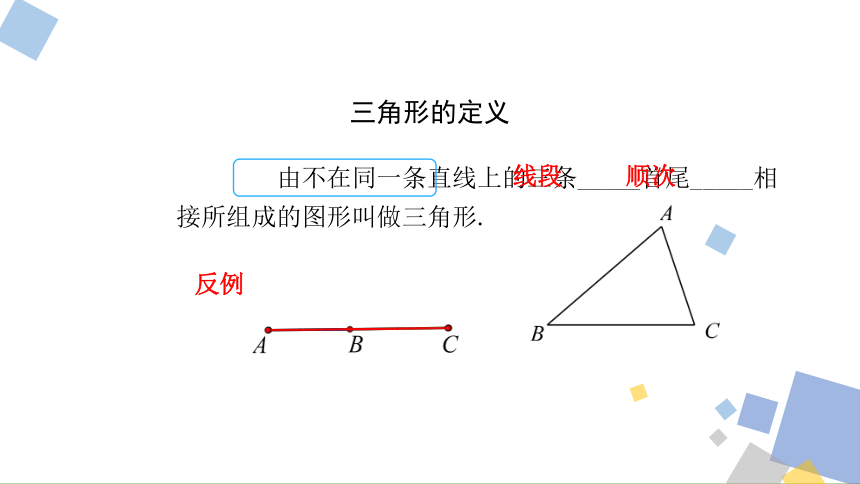
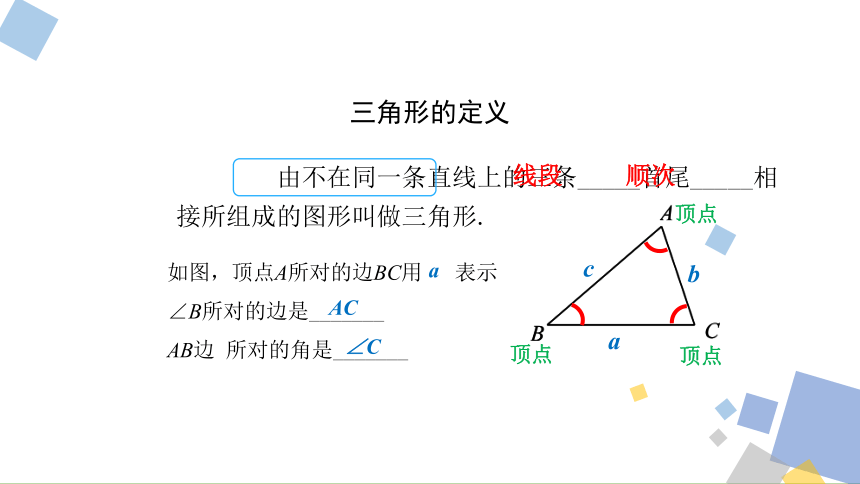
由不在同一条直线上的三条_____首尾_____相
接所组成的图形叫做三角形.
线段
顺次
三角形的定义
反例
由不在同一条直线上的三条_____首尾_____相
接所组成的图形叫做三角形.
线段
顺次
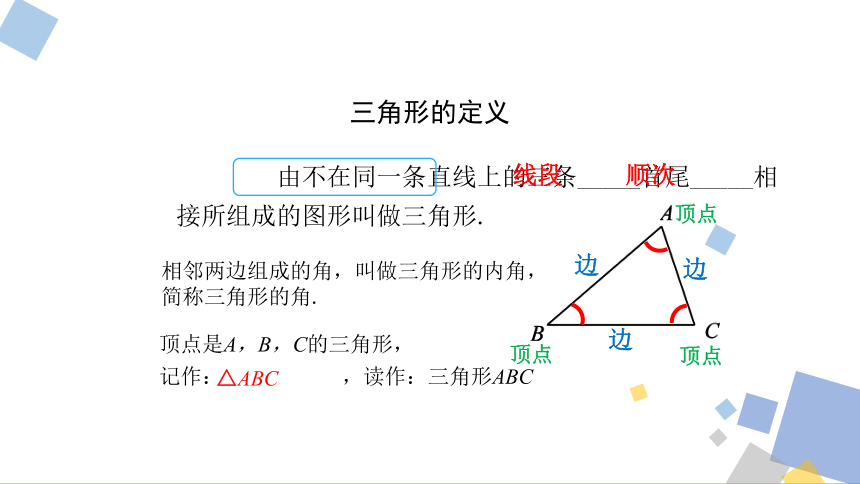
三角形的定义
边
边
边
顶点
顶点
顶点
相邻两边组成的角,叫做三角形的内角,简称三角形的角.
顶点是A,B,C的三角形,
记作: ,读作:三角形ABC
△ABC
由不在同一条直线上的三条_____首尾_____相
接所组成的图形叫做三角形.
三角形的定义
顶点
顶点
顶点
线段
顺次
c
a
b
如图,顶点A所对的边BC用 表示
∠B所对的边是_______
AB边 所对的角是_______
a
AC
∠C
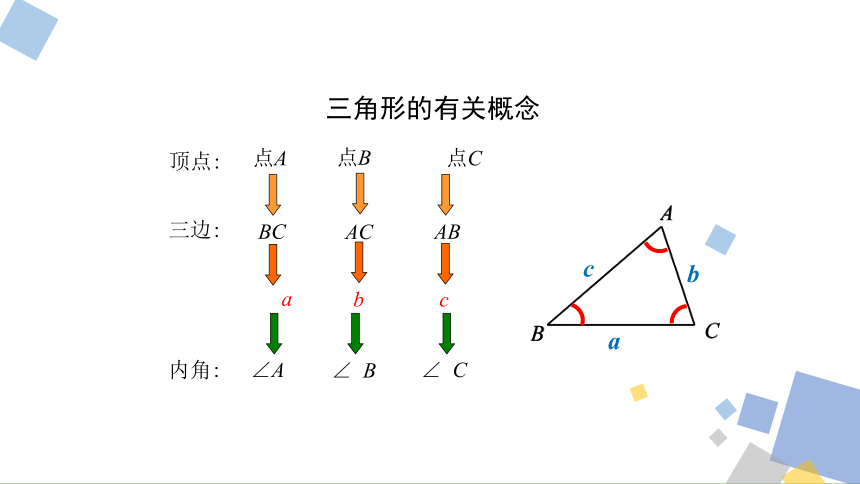
三角形的有关概念
BC
内角:
a
三边:
顶点:
点A
∠A
点B
点C
AC
AB
b
c
∠ B
∠ C
c
a
b
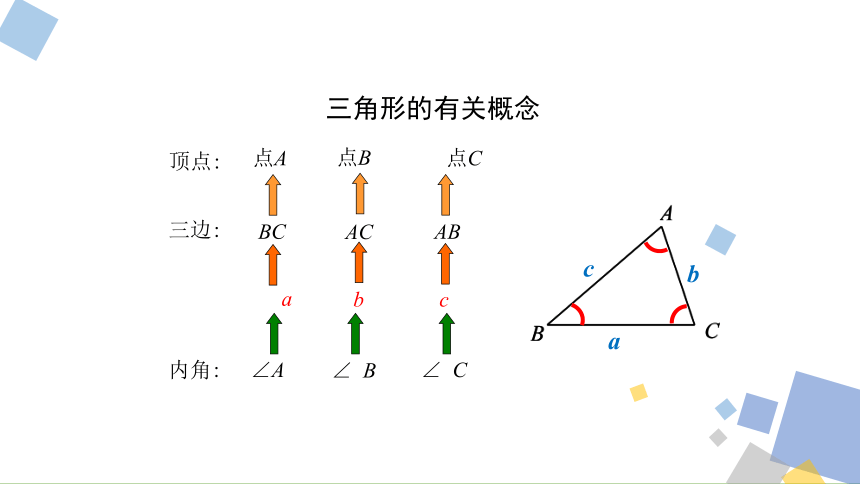
三角形的有关概念
BC
内角:
a
三边:
顶点:
点A
∠A
点B
点C
AC
AB
b
c
∠ B
∠ C
c
a
b
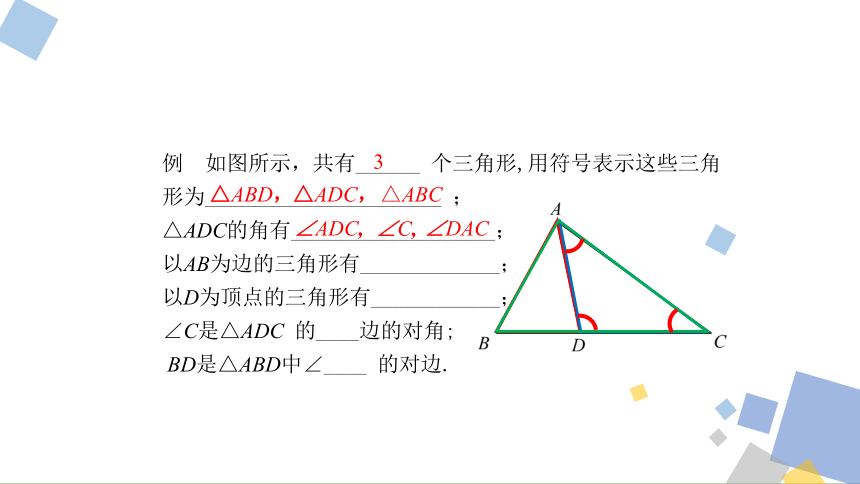
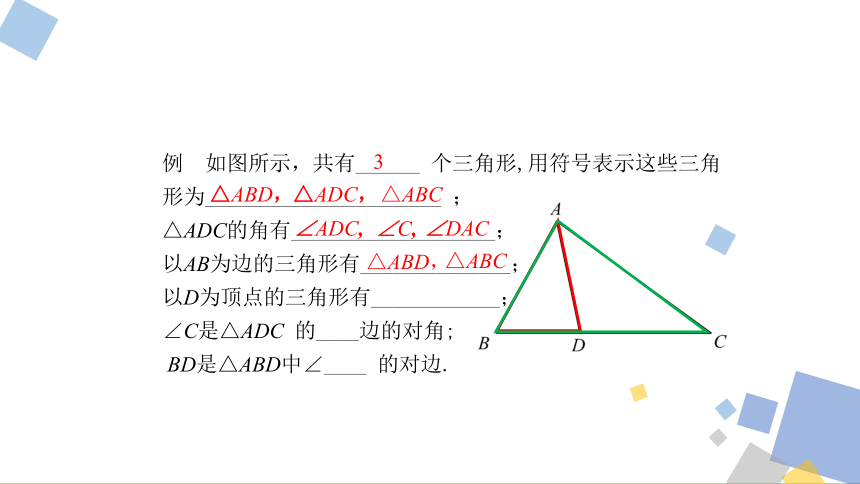
例 如图所示,共有______ 个三角形,用符号表示这些三角
形为______________________ ;
△ADC的角有___________________;
以AB为边的三角形有_____________;
以D为顶点的三角形有____________;
∠C是△ADC 的____边的对角;
BD是△ABD中∠____ 的对边.
3
△ABD,
△ADC,
△ABC
∠ADC,
∠C,
∠DAC
例 如图所示,共有______ 个三角形,用符号表示这些三角
形为______________________ ;
△ADC的角有___________________;
以AB为边的三角形有______________;
以D为顶点的三角形有____________;
∠C是△ADC 的____边的对角;
BD是△ABD中∠____ 的对边.
∠ADC,
∠C,
∠DAC
△ABD,
△ABC
△ABD,
△ADC,
△ABC
3
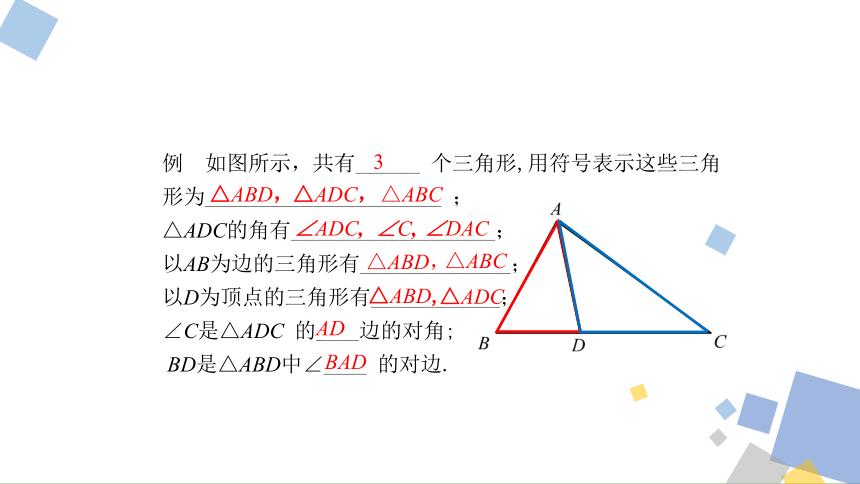
例 如图所示,共有______ 个三角形,用符号表示这些三角
形为______________________ ;
△ADC的角有___________________;
以AB为边的三角形有______________;
以D为顶点的三角形有____________;
∠C是△ADC 的____边的对角;
BD是△ABD中∠____ 的对边.
∠ADC,
∠C,
∠DAC
△ABD,
△ABC
△ABD,
△ADC
AD
BAD
△ABD,
△ADC,
△ABC
3
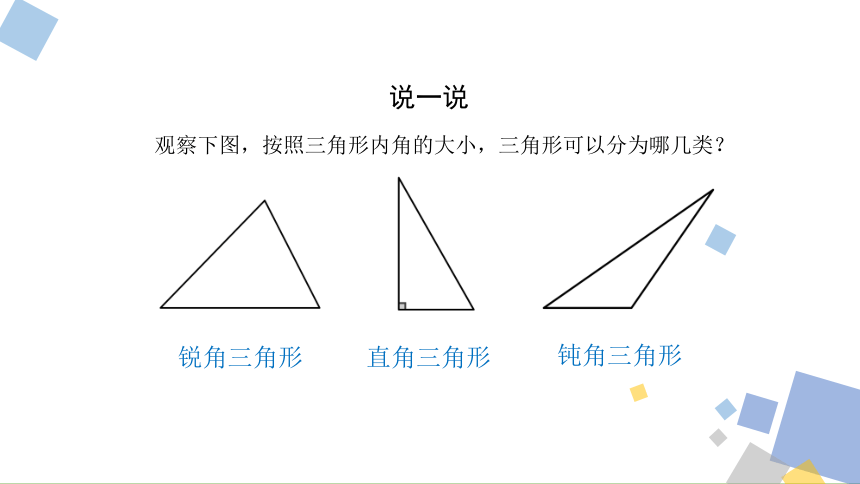
说一说
观察下图,按照三角形内角的大小,三角形可以分为哪几类?
直角三角形
锐角三角形
钝角三角形
想一想
如何按照边的关系对三角形进行分类呢?
三边都不相等的三角形
等腰三角形
腰
腰
底边
顶角
底角
底角
等边三角形
三角形按边的相等关系分类
三角形的分类
三边都
不相等
的三角形
等腰
三角形
等边
三角形
三角形
锐角
三角形
直角
三角形
钝角三角形
三角形
按边的相等关系
按角的大小关系
探 究
任意画一个△ABC,从点B出发,沿着三角形的边到点C,有几条线路可以选择?各条线路的长有什么关系?能证明你的结论吗?
A
B
C
由“两点之间,线段最短”,得
AB+AC >BC
同理,AC+BC>AB
AB+BC>AC
BC>AB-AC
BC>AC-AB
三角形两边的和大于第三边
三角形两边的差小于第三边
三角形三边的关系
三角形两边的和大于_________;
(可用来判断三条线段能否组成三角形)
第三边
第三边
三角形两边的差小于________.
进而得到,三角形第三边的取值范围
两边的差<第三边< 两边的和
例 有两根长度分别为5 cm和8 cm的木棒,用长度为2 cm的木棒与它们能组成三角形吗?为什么?长度为13 cm的木棒呢?
分析:5+8>2,
8+2>5,
5+2<8.
√
×
√
5+8=13,
8+13>5,
5+13>8.
√
√
×
发现:判断三条线段是否可以组成三角形,只需判断两
条较短线段的和是否大于第三条线段即可
解:∵5+2<8,
∴长度为2 cm的木棒与它们不能组成三角形.
∵5+8=13 ,
∴长度为13 cm的木棒与它们也不能组成三角形.
例 有两根长度分别为5 cm和8 cm的木棒,用长度为2 cm的木棒与它们能组成三角形吗?为什么?长度为13 cm的木棒呢?
例 用一条长为18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边长是多少?
(2)能围成有一边长为4 cm的等腰三角形吗?为什么?
分析:
等腰三角形的周长=18 cm,即2倍的腰长+底边长=18 cm.
(1)腰长是底边长的2倍,可设底边长为x cm,列方程可求解.
(2)可能腰长为4 cm, 也可能底边长为4 cm,需分类讨论.
解:(1)设底边长为x cm,则腰长为2x cm,
2ⅹ2x+x=18.
解,得 x=3.6.
∴三边长分别为3.6 cm,7.2 cm ,7.2 cm.
例 用一条长为18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边长是多少?
(2)能围成有一边长为4 cm的等腰三角形吗?为什么?
方程思想
例 用一条长为18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边长是多少?
(2)能围成有一边长为4 cm的等腰三角形吗?为什么?
(2)当底边长为4 cm 时,腰长为
当腰长为4 cm时,底边长为18 -2ⅹ4=10
∵4+4<10,不符合三角形两边的和大于第三边
∴不能围成腰长为4 cm的等腰三角形.
综上,可以围成底边长是4 cm 的等腰三角形.
分类讨论思想
判断能否
围成三角形
已知等腰三角形一边长为4,一边长为6,则等腰三角形的周长为( )
A.14 B.16 C.10 D.14或16
知识点:等腰三角形的概念.
D
思想方法:分类讨论思想.
三角形两边的和大于第三边.
已知等腰三角形一边长为4,一边长为6,则等腰三角形的周长为( )
A.14 B.16 C.10 D.14或16
D
如果把“4”改成“2”,其他条件不变,那么等腰三角形的周长为_____.
知识点:等腰三角形的概念.
思想方法:分类讨论思想.
三角形两边的和大于第三边.
14
拓展提升
6.已知:a、b、c为三角形的三边长,化简:|b+c-a|
+|b-c-a|-|c-a-b|-|a-b+c|.
∴原式=|(b+c)-a|+|b-(c+a)|-|c-(a+b)|-
|(a+c)-b|
=b+c-a+a+c-b-a-b+c+b-a-c
=2c-2a.
解:∵a、b、c为三角形三边的长,
∴a+b>c,a+c>b,b+c>a,
思 考
盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?
动手操作
用三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗
通过实验得出结论:它的形状不会改变.
用四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗
通过实验得出结论:它的形状会改变.
在四边形的木架上再钉一根木条,将它的一对顶点连接起来,然后扭动它,它的形状会改变吗
通过实验得出结论:它的形状不会改变.
经过以上三次实验,你发现了什么规律
发现,
三角形木架的形状不会改变,而四边形木架的形状会改变.
三角形是具有稳定性的图形,而四边形没有稳定性.
与三角形有关的线段
三角形的边
三角形的高
三角形的中线
三角形的角平分线
c
a
b
1
2
三角形的高线:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线.
锐角三角形三条高线交于三角形内部一点;
直角三角形三条高线交于直角顶点;
钝角三角形三条高线所在直线交于三角形外部一点.
例:如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,求BP的最小值.
解:根据垂线段最短,可知当BP⊥AC时,BP有最小值.
由△ABC的面积公式可知,
AD·BC = BP·AC.
代入数值,可解得BP=4×6÷5=4.8 .
面积法应用
三角形的中线:连接三角形一个顶点与它对边中点的线段叫做三角形的中线.
三角形的中线将三角形分成面积相等的两部分.
三角形的中线:连接三角形一个顶点与它对边中点的线段叫做三角形的中线.
三角形的中线将三角形分成面积相等的两部分.
三角形的三条中线交于三角形内部一点,这个交点叫做三角形的重心.
例:如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,求S△ADF-S△BEF的值.
解:∵点D是AC的中点,∴AD= AC.
∵S△ABC=12,∴S△ABD= S△ABC= ×12=6.
∵EC=2BE,S△ABC=12,∴S△ABE= S△ABC= ×12=4.
方法总结:三角形的中线将三角形分成面积相等的两部分;高相等时,面积的比等于底边的比;底相等时,面积的比等于高的比.
∵S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)=S△ADF-S△BEF,
即S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
三角形的角平分线:三角形一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.三角形的三条角平分线交于三角形内部一点.
角平分线模型
例 如图1,在△ABC中,BD平分∠ABC ,CE平分∠ACB,BD与AC相交于点O. 若∠ABC=40° , ∠ACB=60°,则∠BOC= .
图1
条件①:∠ABC=40°;
条件②: BD平分∠ABC;
条件③:∠ACB=60°;
条件④: CE平分∠ACB;
条件⑤:三角形的内角和为180°.
图1
∠BOC的大小
∠OBC
条件①②
∠OCB
条件③④
在△OBC 中
条件⑤
分析:
∵ CE平分∠ACB,∠ACB=60°,
∵BD平分∠ABC ,∠ABC=40° ,
∴ ∠ABD= ∠DBC= ∠ABC= 20°.
∴ ∠ACE= ∠ECB= ∠ACB= 30°.
在△OBC 中,
∵ ∠DBC+ ∠ECB+∠BOC=180°,
∴ ∠BOC= 130°.
图1
解:
另解:
∵ CE平分∠ACB,∠ACB=60°,
∵BD平分∠ABC ,∠ABC=40° ,
∴ ∠ABD= ∠DBC= ∠ABC= 20°.
∴ ∠ACE= ∠ECB= ∠ACB= 30°.
图1
变式 将例题中的条件“若∠ABC=40° , ∠ACB=60°”变成“若∠A=80°” ,则∠BOC= .
图1
条件②: BD平分∠ABC;
条件④: CE平分∠ACB;
条件⑤:三角形的内角和为180°;
条件⑥: ∠A=80°.
图1
条件⑥
条件⑤
△ABC 中
∠ABC+ ∠ACB
条件②
条件④
∠DBC+ ∠ECB
条件⑤
在△BOC 中
∠BOC的大小
分析:
解:在△ABC中, ∵ ∠ABC+ ∠ACB+∠A=180°,∠A=80°,
∴∠ABC+ ∠ACB= 100°,
∵ CE平分∠ACB,
∵BD平分∠ABC ,
∴ ∠ABD= ∠DBC= ∠ABC.
∴ ∠ACE= ∠ECB= ∠ACB.
图1
∴ ∠DBC+ ∠ECB
= ∠ABC+ ∠ACB
= (∠ABC +∠ACB)
= 50°.
在△OBC 中,
∵ ∠DBC+ ∠ECB+∠BOC=180°,
∴ ∠BOC= 130°.
图1
解后反思
在解决问题的过程中,如果不能求出需要的每一个量,可以考虑用整体思想解决问题.
变式 将例题中的条件“若∠ABC=40° , ∠ACB=60°”去掉,∠BOC与∠A有怎样的数量关系?
图1
条件②: BD平分∠ABC;
条件④: CE平分∠ACB;
条件⑤:三角形的内角和为180°.
图1
条件⑤
△ABC 中
∠ABC+ ∠ACB与∠A的关系
条件②
条件④
∠DBC+ ∠ECB与∠A的关系
∠BOC与∠A的关系
条件⑤
△BOC 中
分析:
解
解:在△ABC中, ∵ ∠ABC+ ∠ACB+∠A=180°,
∴∠ABC+ ∠ACB= 180°- ∠A.
∵ CE平分∠ACB,
∵BD平分∠ABC ,
∴ ∠DBC= ∠ABC.
∴ ∠ECB= ∠ACB.
图1
∴ ∠DBC+ ∠ECB
= ∠ABC+ ∠ACB
= (∠ABC +∠ACB)
= (180°- ∠A).
图1
在△OBC 中,
∵ ∠DBC+ ∠ECB+∠BOC=180°,
∴ ∠BOC= 180°-(∠DBC+ ∠ECB)
= 180°- (180°- ∠A).
= 90°+ ∠A.
图1
角平分线模型
变式 如图2,将例题中的条件“两条角平分线交于点O”换成“两条高线交于点O”,将“若∠ABC=40° , ∠ACB=60°”去掉,∠BOC与∠A又有怎样的数量关系?
从特殊到一般
图2
不妨设若∠ABC=40° , ∠ACB=60°,求∠BOC.
图2
分析:
图2
∠BOC的大小
∠OBC
条件①④
∠OCB
条件②③
在△OBC 中
条件⑤
条件①:∠ABC=40°;条件②: BD⊥AC;
条件③:∠ACB=60°;条件④: CE⊥AB;
条件⑤:三角形的内角和为180°.
分析:
图2
分析:接下来我们依然假设∠A=80° ,求∠BOC.
图2
条件②: BD⊥AC;条件④: CE⊥AB;
条件⑤:三角形的内角和为180°;
条件⑥: ∠A=80° .
条件⑥
条件⑤
△ABC 中
∠ABC+ ∠ACB
条件②
条件④
∠DBC+ ∠ECB
条件⑤
△BOC 中
∠BOC
的大小
分析:
图2
分析:回到本题要研究的问题:∠BOC与∠A的数量关系.
图2
条件②: BD⊥AC;条件④: CE⊥AB;
条件⑤:三角形的内角和为180°.
条件⑤
△ABC 中
∠ABC+ ∠ACB与∠A的关系
条件②
条件④
∠DBC+ ∠ECB与∠A的关系
条件⑤
△BOC 中
∠BOC与∠A的关系
分析:
解:在△ABC中, ∵ ∠ABC+ ∠ACB+∠A=180°,
∴∠ABC+ ∠ACB= 180°-∠A.
∵BD⊥AC ,
∴ ∠ BDC= 90°, △BDC为直角三角形.
∴ ∠ACB与∠DBC互余,
即∠DBC = 90° -∠ACB.
图2
同理可得, ∠ECB = 90° -∠ABC.
∴ ∠DBC+ ∠ECB
= 90°-∠ACB + 90°-∠ABC
= 180°- (∠ABC +∠ACB)
=180°- (180°-∠A)
= ∠A.
图2
在△OBC 中,
∵ ∠DBC+ ∠ECB+∠BOC=180°,
∴ ∠BOC= 180°- (∠DBC+ ∠ECB)
= 180°- ∠A.
图2
解后反思
(1)这个变式的研究,可以从例题及前面两个变式的研究过程中得到启发,虽然条件②、④发生了变化,但从条件②、④中依然可以得到∠DBC和∠ECB的度数,所以仍然可以按照同样的方法解决问题.
解后反思
(2)其他解决问题的方法.
思路2:(利用外角)
∠BOC与∠A的关系
∠ABO与 ∠A 的关系
条件②
△BOE 的外角
条件④
∠BEC=90°
条件②: BD⊥AC;条件④: CE⊥AB.
图2
解后反思
思路3:(利用对顶角)
图2
图2
解后反思
思路3:(利用对顶角)
图2
解后反思
思路3:(利用对顶角)
图2
∴ ∠ BDA= 90°, ∠CEA= 90°.
在四边形AEOD中,
∵ ∠A+ ∠CEA+ ∠BDA+∠EOD=360°,
∴ ∠A+ ∠EOD=180°.
∴ ∠EOD=180°- ∠A.
∴ ∠BOC= ∠EOD=180°- ∠A.
∵BD⊥AC , CE⊥AB,
解后反思
思路3:(利用对顶角)
解后反思
(3)三角形中求角的大小问题,可以从三角形的内角和、三角形外角的性质,对顶角以及邻补角的角度来考虑.
BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是_____.
分析:
△ABD的周长=AB+BD+AD
△BCD的周长=BC+BD+DC
△ABD的周长-△BCD的周长
=AB-BC
在△ABC中, ∠ACB=90°, CD是AB边上的高, AB=13 cm,BC=12 cm,AC=5 cm,
(1)CD的长为 cm ;
(2)若AE是BC边上的中线,则△ABE的面积为 cm .
分析:
S△ABC= AB CD= BC AC
13CD=12 5
认识三角形
生活中的三角形
请你根据小学认识的三角形,判断下列图形是三角形吗?
是三角形的,在括号内打“√”,不是三角形的,打“×”.
( ) ( ) ( ) ( ) ( )
√
×
×
×
×
由不在同一条直线上的三条_____首尾_____相
接所组成的图形叫做三角形.
线段
顺次
三角形的定义
反例
由不在同一条直线上的三条_____首尾_____相
接所组成的图形叫做三角形.
线段
顺次
三角形的定义
边
边
边
顶点
顶点
顶点
相邻两边组成的角,叫做三角形的内角,简称三角形的角.
顶点是A,B,C的三角形,
记作: ,读作:三角形ABC
△ABC
由不在同一条直线上的三条_____首尾_____相
接所组成的图形叫做三角形.
三角形的定义
顶点
顶点
顶点
线段
顺次
c
a
b
如图,顶点A所对的边BC用 表示
∠B所对的边是_______
AB边 所对的角是_______
a
AC
∠C
三角形的有关概念
BC
内角:
a
三边:
顶点:
点A
∠A
点B
点C
AC
AB
b
c
∠ B
∠ C
c
a
b
三角形的有关概念
BC
内角:
a
三边:
顶点:
点A
∠A
点B
点C
AC
AB
b
c
∠ B
∠ C
c
a
b
例 如图所示,共有______ 个三角形,用符号表示这些三角
形为______________________ ;
△ADC的角有___________________;
以AB为边的三角形有_____________;
以D为顶点的三角形有____________;
∠C是△ADC 的____边的对角;
BD是△ABD中∠____ 的对边.
3
△ABD,
△ADC,
△ABC
∠ADC,
∠C,
∠DAC
例 如图所示,共有______ 个三角形,用符号表示这些三角
形为______________________ ;
△ADC的角有___________________;
以AB为边的三角形有______________;
以D为顶点的三角形有____________;
∠C是△ADC 的____边的对角;
BD是△ABD中∠____ 的对边.
∠ADC,
∠C,
∠DAC
△ABD,
△ABC
△ABD,
△ADC,
△ABC
3
例 如图所示,共有______ 个三角形,用符号表示这些三角
形为______________________ ;
△ADC的角有___________________;
以AB为边的三角形有______________;
以D为顶点的三角形有____________;
∠C是△ADC 的____边的对角;
BD是△ABD中∠____ 的对边.
∠ADC,
∠C,
∠DAC
△ABD,
△ABC
△ABD,
△ADC
AD
BAD
△ABD,
△ADC,
△ABC
3
说一说
观察下图,按照三角形内角的大小,三角形可以分为哪几类?
直角三角形
锐角三角形
钝角三角形
想一想
如何按照边的关系对三角形进行分类呢?
三边都不相等的三角形
等腰三角形
腰
腰
底边
顶角
底角
底角
等边三角形
三角形按边的相等关系分类
三角形的分类
三边都
不相等
的三角形
等腰
三角形
等边
三角形
三角形
锐角
三角形
直角
三角形
钝角三角形
三角形
按边的相等关系
按角的大小关系
探 究
任意画一个△ABC,从点B出发,沿着三角形的边到点C,有几条线路可以选择?各条线路的长有什么关系?能证明你的结论吗?
A
B
C
由“两点之间,线段最短”,得
AB+AC >BC
同理,AC+BC>AB
AB+BC>AC
BC>AB-AC
BC>AC-AB
三角形两边的和大于第三边
三角形两边的差小于第三边
三角形三边的关系
三角形两边的和大于_________;
(可用来判断三条线段能否组成三角形)
第三边
第三边
三角形两边的差小于________.
进而得到,三角形第三边的取值范围
两边的差<第三边< 两边的和
例 有两根长度分别为5 cm和8 cm的木棒,用长度为2 cm的木棒与它们能组成三角形吗?为什么?长度为13 cm的木棒呢?
分析:5+8>2,
8+2>5,
5+2<8.
√
×
√
5+8=13,
8+13>5,
5+13>8.
√
√
×
发现:判断三条线段是否可以组成三角形,只需判断两
条较短线段的和是否大于第三条线段即可
解:∵5+2<8,
∴长度为2 cm的木棒与它们不能组成三角形.
∵5+8=13 ,
∴长度为13 cm的木棒与它们也不能组成三角形.
例 有两根长度分别为5 cm和8 cm的木棒,用长度为2 cm的木棒与它们能组成三角形吗?为什么?长度为13 cm的木棒呢?
例 用一条长为18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边长是多少?
(2)能围成有一边长为4 cm的等腰三角形吗?为什么?
分析:
等腰三角形的周长=18 cm,即2倍的腰长+底边长=18 cm.
(1)腰长是底边长的2倍,可设底边长为x cm,列方程可求解.
(2)可能腰长为4 cm, 也可能底边长为4 cm,需分类讨论.
解:(1)设底边长为x cm,则腰长为2x cm,
2ⅹ2x+x=18.
解,得 x=3.6.
∴三边长分别为3.6 cm,7.2 cm ,7.2 cm.
例 用一条长为18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边长是多少?
(2)能围成有一边长为4 cm的等腰三角形吗?为什么?
方程思想
例 用一条长为18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边长是多少?
(2)能围成有一边长为4 cm的等腰三角形吗?为什么?
(2)当底边长为4 cm 时,腰长为
当腰长为4 cm时,底边长为18 -2ⅹ4=10
∵4+4<10,不符合三角形两边的和大于第三边
∴不能围成腰长为4 cm的等腰三角形.
综上,可以围成底边长是4 cm 的等腰三角形.
分类讨论思想
判断能否
围成三角形
已知等腰三角形一边长为4,一边长为6,则等腰三角形的周长为( )
A.14 B.16 C.10 D.14或16
知识点:等腰三角形的概念.
D
思想方法:分类讨论思想.
三角形两边的和大于第三边.
已知等腰三角形一边长为4,一边长为6,则等腰三角形的周长为( )
A.14 B.16 C.10 D.14或16
D
如果把“4”改成“2”,其他条件不变,那么等腰三角形的周长为_____.
知识点:等腰三角形的概念.
思想方法:分类讨论思想.
三角形两边的和大于第三边.
14
拓展提升
6.已知:a、b、c为三角形的三边长,化简:|b+c-a|
+|b-c-a|-|c-a-b|-|a-b+c|.
∴原式=|(b+c)-a|+|b-(c+a)|-|c-(a+b)|-
|(a+c)-b|
=b+c-a+a+c-b-a-b+c+b-a-c
=2c-2a.
解:∵a、b、c为三角形三边的长,
∴a+b>c,a+c>b,b+c>a,
思 考
盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?
动手操作
用三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗
通过实验得出结论:它的形状不会改变.
用四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗
通过实验得出结论:它的形状会改变.
在四边形的木架上再钉一根木条,将它的一对顶点连接起来,然后扭动它,它的形状会改变吗
通过实验得出结论:它的形状不会改变.
经过以上三次实验,你发现了什么规律
发现,
三角形木架的形状不会改变,而四边形木架的形状会改变.
三角形是具有稳定性的图形,而四边形没有稳定性.
与三角形有关的线段
三角形的边
三角形的高
三角形的中线
三角形的角平分线
c
a
b
1
2
三角形的高线:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线.
锐角三角形三条高线交于三角形内部一点;
直角三角形三条高线交于直角顶点;
钝角三角形三条高线所在直线交于三角形外部一点.
例:如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,求BP的最小值.
解:根据垂线段最短,可知当BP⊥AC时,BP有最小值.
由△ABC的面积公式可知,
AD·BC = BP·AC.
代入数值,可解得BP=4×6÷5=4.8 .
面积法应用
三角形的中线:连接三角形一个顶点与它对边中点的线段叫做三角形的中线.
三角形的中线将三角形分成面积相等的两部分.
三角形的中线:连接三角形一个顶点与它对边中点的线段叫做三角形的中线.
三角形的中线将三角形分成面积相等的两部分.
三角形的三条中线交于三角形内部一点,这个交点叫做三角形的重心.
例:如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,求S△ADF-S△BEF的值.
解:∵点D是AC的中点,∴AD= AC.
∵S△ABC=12,∴S△ABD= S△ABC= ×12=6.
∵EC=2BE,S△ABC=12,∴S△ABE= S△ABC= ×12=4.
方法总结:三角形的中线将三角形分成面积相等的两部分;高相等时,面积的比等于底边的比;底相等时,面积的比等于高的比.
∵S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)=S△ADF-S△BEF,
即S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
三角形的角平分线:三角形一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.三角形的三条角平分线交于三角形内部一点.
角平分线模型
例 如图1,在△ABC中,BD平分∠ABC ,CE平分∠ACB,BD与AC相交于点O. 若∠ABC=40° , ∠ACB=60°,则∠BOC= .
图1
条件①:∠ABC=40°;
条件②: BD平分∠ABC;
条件③:∠ACB=60°;
条件④: CE平分∠ACB;
条件⑤:三角形的内角和为180°.
图1
∠BOC的大小
∠OBC
条件①②
∠OCB
条件③④
在△OBC 中
条件⑤
分析:
∵ CE平分∠ACB,∠ACB=60°,
∵BD平分∠ABC ,∠ABC=40° ,
∴ ∠ABD= ∠DBC= ∠ABC= 20°.
∴ ∠ACE= ∠ECB= ∠ACB= 30°.
在△OBC 中,
∵ ∠DBC+ ∠ECB+∠BOC=180°,
∴ ∠BOC= 130°.
图1
解:
另解:
∵ CE平分∠ACB,∠ACB=60°,
∵BD平分∠ABC ,∠ABC=40° ,
∴ ∠ABD= ∠DBC= ∠ABC= 20°.
∴ ∠ACE= ∠ECB= ∠ACB= 30°.
图1
变式 将例题中的条件“若∠ABC=40° , ∠ACB=60°”变成“若∠A=80°” ,则∠BOC= .
图1
条件②: BD平分∠ABC;
条件④: CE平分∠ACB;
条件⑤:三角形的内角和为180°;
条件⑥: ∠A=80°.
图1
条件⑥
条件⑤
△ABC 中
∠ABC+ ∠ACB
条件②
条件④
∠DBC+ ∠ECB
条件⑤
在△BOC 中
∠BOC的大小
分析:
解:在△ABC中, ∵ ∠ABC+ ∠ACB+∠A=180°,∠A=80°,
∴∠ABC+ ∠ACB= 100°,
∵ CE平分∠ACB,
∵BD平分∠ABC ,
∴ ∠ABD= ∠DBC= ∠ABC.
∴ ∠ACE= ∠ECB= ∠ACB.
图1
∴ ∠DBC+ ∠ECB
= ∠ABC+ ∠ACB
= (∠ABC +∠ACB)
= 50°.
在△OBC 中,
∵ ∠DBC+ ∠ECB+∠BOC=180°,
∴ ∠BOC= 130°.
图1
解后反思
在解决问题的过程中,如果不能求出需要的每一个量,可以考虑用整体思想解决问题.
变式 将例题中的条件“若∠ABC=40° , ∠ACB=60°”去掉,∠BOC与∠A有怎样的数量关系?
图1
条件②: BD平分∠ABC;
条件④: CE平分∠ACB;
条件⑤:三角形的内角和为180°.
图1
条件⑤
△ABC 中
∠ABC+ ∠ACB与∠A的关系
条件②
条件④
∠DBC+ ∠ECB与∠A的关系
∠BOC与∠A的关系
条件⑤
△BOC 中
分析:
解
解:在△ABC中, ∵ ∠ABC+ ∠ACB+∠A=180°,
∴∠ABC+ ∠ACB= 180°- ∠A.
∵ CE平分∠ACB,
∵BD平分∠ABC ,
∴ ∠DBC= ∠ABC.
∴ ∠ECB= ∠ACB.
图1
∴ ∠DBC+ ∠ECB
= ∠ABC+ ∠ACB
= (∠ABC +∠ACB)
= (180°- ∠A).
图1
在△OBC 中,
∵ ∠DBC+ ∠ECB+∠BOC=180°,
∴ ∠BOC= 180°-(∠DBC+ ∠ECB)
= 180°- (180°- ∠A).
= 90°+ ∠A.
图1
角平分线模型
变式 如图2,将例题中的条件“两条角平分线交于点O”换成“两条高线交于点O”,将“若∠ABC=40° , ∠ACB=60°”去掉,∠BOC与∠A又有怎样的数量关系?
从特殊到一般
图2
不妨设若∠ABC=40° , ∠ACB=60°,求∠BOC.
图2
分析:
图2
∠BOC的大小
∠OBC
条件①④
∠OCB
条件②③
在△OBC 中
条件⑤
条件①:∠ABC=40°;条件②: BD⊥AC;
条件③:∠ACB=60°;条件④: CE⊥AB;
条件⑤:三角形的内角和为180°.
分析:
图2
分析:接下来我们依然假设∠A=80° ,求∠BOC.
图2
条件②: BD⊥AC;条件④: CE⊥AB;
条件⑤:三角形的内角和为180°;
条件⑥: ∠A=80° .
条件⑥
条件⑤
△ABC 中
∠ABC+ ∠ACB
条件②
条件④
∠DBC+ ∠ECB
条件⑤
△BOC 中
∠BOC
的大小
分析:
图2
分析:回到本题要研究的问题:∠BOC与∠A的数量关系.
图2
条件②: BD⊥AC;条件④: CE⊥AB;
条件⑤:三角形的内角和为180°.
条件⑤
△ABC 中
∠ABC+ ∠ACB与∠A的关系
条件②
条件④
∠DBC+ ∠ECB与∠A的关系
条件⑤
△BOC 中
∠BOC与∠A的关系
分析:
解:在△ABC中, ∵ ∠ABC+ ∠ACB+∠A=180°,
∴∠ABC+ ∠ACB= 180°-∠A.
∵BD⊥AC ,
∴ ∠ BDC= 90°, △BDC为直角三角形.
∴ ∠ACB与∠DBC互余,
即∠DBC = 90° -∠ACB.
图2
同理可得, ∠ECB = 90° -∠ABC.
∴ ∠DBC+ ∠ECB
= 90°-∠ACB + 90°-∠ABC
= 180°- (∠ABC +∠ACB)
=180°- (180°-∠A)
= ∠A.
图2
在△OBC 中,
∵ ∠DBC+ ∠ECB+∠BOC=180°,
∴ ∠BOC= 180°- (∠DBC+ ∠ECB)
= 180°- ∠A.
图2
解后反思
(1)这个变式的研究,可以从例题及前面两个变式的研究过程中得到启发,虽然条件②、④发生了变化,但从条件②、④中依然可以得到∠DBC和∠ECB的度数,所以仍然可以按照同样的方法解决问题.
解后反思
(2)其他解决问题的方法.
思路2:(利用外角)
∠BOC与∠A的关系
∠ABO与 ∠A 的关系
条件②
△BOE 的外角
条件④
∠BEC=90°
条件②: BD⊥AC;条件④: CE⊥AB.
图2
解后反思
思路3:(利用对顶角)
图2
图2
解后反思
思路3:(利用对顶角)
图2
解后反思
思路3:(利用对顶角)
图2
∴ ∠ BDA= 90°, ∠CEA= 90°.
在四边形AEOD中,
∵ ∠A+ ∠CEA+ ∠BDA+∠EOD=360°,
∴ ∠A+ ∠EOD=180°.
∴ ∠EOD=180°- ∠A.
∴ ∠BOC= ∠EOD=180°- ∠A.
∵BD⊥AC , CE⊥AB,
解后反思
思路3:(利用对顶角)
解后反思
(3)三角形中求角的大小问题,可以从三角形的内角和、三角形外角的性质,对顶角以及邻补角的角度来考虑.
BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是_____.
分析:
△ABD的周长=AB+BD+AD
△BCD的周长=BC+BD+DC
△ABD的周长-△BCD的周长
=AB-BC
在△ABC中, ∠ACB=90°, CD是AB边上的高, AB=13 cm,BC=12 cm,AC=5 cm,
(1)CD的长为 cm ;
(2)若AE是BC边上的中线,则△ABE的面积为 cm .
分析:
S△ABC= AB CD= BC AC
13CD=12 5
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
