第3章 数据分析初步单元测试卷(标准难度)(含解析)
文档属性
| 名称 | 第3章 数据分析初步单元测试卷(标准难度)(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 379.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-14 19:01:58 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版初中数学八年级下册第三单元《数据分析初步》单元测试卷
考试范围:第三单元;考试时间:120分钟;总分:120分
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.某次射击训练中,一小组的成绩如表所示:已知该小组的平均成绩为环,那么成绩为环的人数是
( )
环数
人数
A. 人 B. 人 C. 人 D. 人
2.某工厂生产质量分别为,,,四种规格的球,现从中取个球装到一个空箱子里,这时箱子里球的平均质量为,若再放入一个的球,此时箱子里球的平均质量变为,则的值为
( )
A. B. C. D.
3.一个小组有名学生,如果名学生的平均成绩是分,另外名学生每人得分,那么整个小组的平均成绩是( )
A. 分 B. 分 C. 分 D. 分
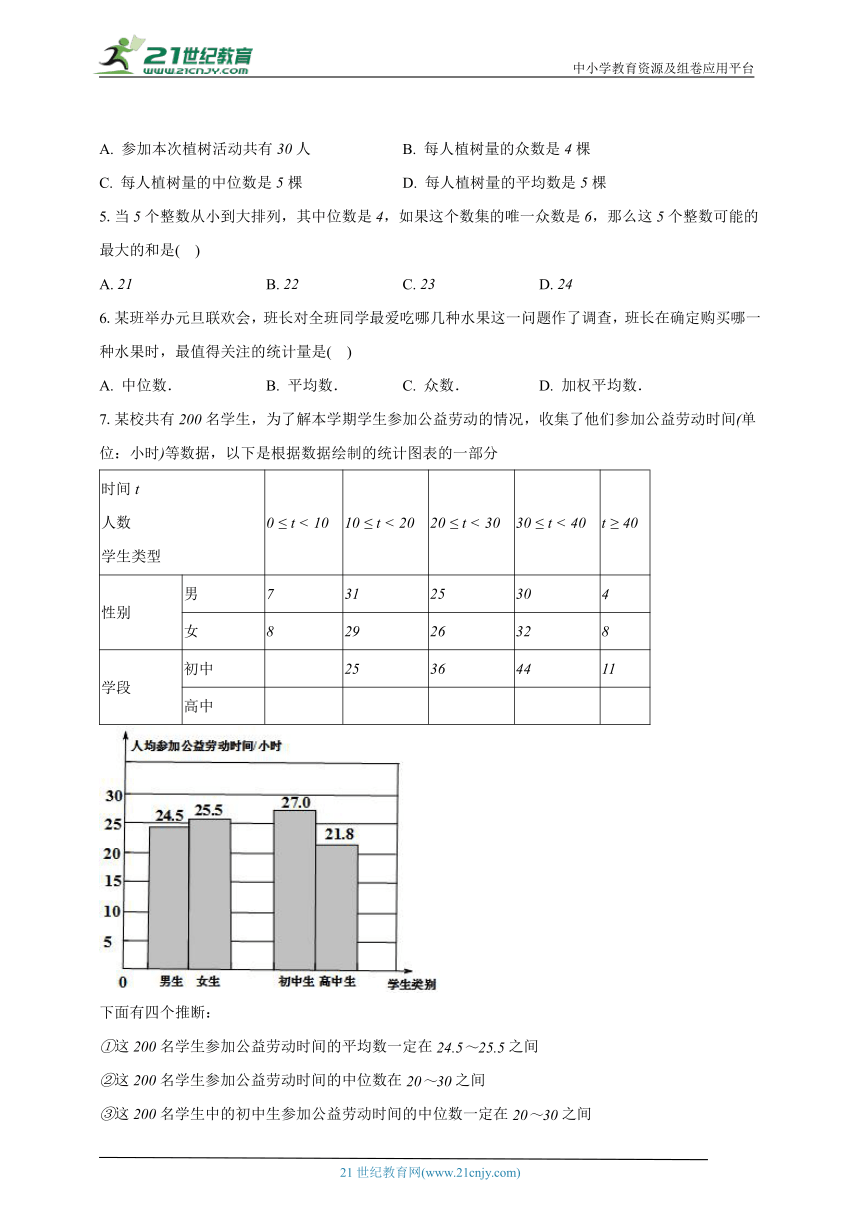
4.某单位组织职工开展植树活动,植树量与人数之间关系如图,下列说法不正确的是( )
A. 参加本次植树活动共有人 B. 每人植树量的众数是棵
C. 每人植树量的中位数是棵 D. 每人植树量的平均数是棵
5.当个整数从小到大排列,其中位数是,如果这个数集的唯一众数是,那么这个整数可能的最大的和是( )
A. B. C. D.
6.某班举办元旦联欢会,班长对全班同学最爱吃哪几种水果这一问题作了调查,班长在确定购买哪一种水果时,最值得关注的统计量是( )
A. 中位数. B. 平均数. C. 众数. D. 加权平均数.
7.某校共有名学生,为了解本学期学生参加公益劳动的情况,收集了他们参加公益劳动时间单位:小时等数据,以下是根据数据绘制的统计图表的一部分
时间
人数
学生类型
性别 男
女
学段 初中
高中
下面有四个推断:
这名学生参加公益劳动时间的平均数一定在之间
这名学生参加公益劳动时间的中位数在之间
这名学生中的初中生参加公益劳动时间的中位数一定在之间
这名学生中的高中生参加公益劳动时间的中位数可能在之间
所有合理推断的序号是( )
A. B. C. D.
8.若数据,,,,,,的方差是,则数据,,,,,,的方差是
( )
A. B. C. D.
9.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续天,每天新增疑似病例不超过人”下列新增疑似病例的数据中,一定符合该标志的是( )
A. 平均数是,中位数是 B. 平均数是,总体方差是
C. 中位数是,众数是 D. 平均数是,方差大于
10.在对一组样本数据进行分析时,小华列出了方差的计算公式:
.
由公式提供的信息,得到以下四个结论:样本的容量是;样本的中位数是;样本的众数是;样本的平均数是其中正确的是
( )
A. B. C. D.
11.某校在读书系列活动中,为了解学生的课外阅读情况,随机选取了八年级某班甲、乙两组学生一周的课外阅读时间单位:进行统计,数据如图表,两组数据的平均数分别为、,方差分别为、,则( )
甲组
乙组
A. , B. ,
C. , D. ,
12.家乐福超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如表:
测试项目 创新能力 综合知识 语言表达
测试成绩分数
将创新能力、综合知识和语言表达三项测试成绩按的比分计入总成绩,则该应聘者的总成绩是
分.( )
A. B. C. D. 以上都不对
二、填空题:本题共4小题,每小题3分,共12分。
13.棉农种植了一亩地的良种棉,这亩棉约种了株,在棉花采摘时,棉农随机确定了株棉花进行分摘,等采摘完后称这株棉花,产籽棉的质量如下表所示:
棉株数
单株产量
这株棉花的平均产量为 ,并根据计算估计这亩地的棉花产量是 亩,市制面积单位
14.从甲、乙、丙三个厂家生产的同一种产品中各抽取件,对它们的使用寿命进行跟踪调查,结果如下单位:年:
甲:,,,,,,,;
乙:,,,,,,,;
丙:,,,,,,,.
三个厂家在广告中都称该产品的使用寿命是年.请根据结果判断,厂家在广告中分别运用了平均数、众数、中位数中的哪一种集中趋势的特征数:甲: ,乙: ,丙: .
15.两组数据:,,,与,,的平均数都是若将这两组数据合并为一组新数据,则这组新数据的众数为 .
16.将甲、乙两组各个数据绘制成折线统计图如图,两组数据的平均数都是,设甲、乙两组数据的方差分别为则 填“”“”或“”.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
为了响应“五水共治,建设美丽家园”的号召,某小区业委会随机调查了该小区户家庭月的用水量,结果如下表所示:
月用水量
户数
计算这户家庭月的平均用水量.
若该小区有户家庭,估计该小区月的用水量为多少吨?
18.本小题分
某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛现有甲、乙两个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录甲、乙两个小组各项得分如下表:
小组 研究报告 小组展示 答辩
甲
乙
计算各小组的平均成绩,并从高分到低分确定小组的排名顺序
如果研究报告、小组展示、答辩按照计算成绩,哪个小组的成绩最高
19.本小题分
某学校评选先进班集体,从“学习”“卫生”“纪律”“活动参与”四个方面考核打分,各项满分均为分,所占比例如下表:
项目 学习 卫生 纪律 活动参与
所占比例
八年级班这四项得分依次为,,,,若学校规定班级四项综合得分超过分的将会获得“先进班集体”称号,请你通过计算说明该班是否会获得“先进班集体”称号
20.本小题分
甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下:单位:年
甲厂:,,,,,,,,,
乙厂:,,,,,,,,,
丙厂:,,,,,,,,,
请回答下面问题:
填空:
平均数 众数 中位数
甲厂
乙厂
丙厂
这三个厂家的销售广告分别利用了哪一种表示集中趋势的特征数
你是顾客,你买三家中哪一家的电子产品为什么
21.本小题分
为提高节水意识,小申随机统计了自己家天的用水量,并分析了第天的用水情况,将得到的数据进行整理后,绘制成统计图单位:升
求这天内小申家每天用水量的平均数和中位数.
求第天小申家洗衣服的水占这一天总用水量的百分比.
请你根据统计图中的信息,给小申家提出一条合理的节约用水建议,并估算采用你的建议后小申家一个月按天计算节约的用水量.
22.本小题分
下表是从某校八年级名女生中随机抽取的名女生的身高统计表.
身高
人数
依据样本,估计该校八年级女生的平均身高.
写出这名女生身高的中位数和众数.
请你依据这个样本,设计一个挑选名女生组成方队的方案要求选中女生的身高尽可能接近
23.本小题分
希望中学八年级学生开展踢毽子活动,每班派名学生参加,按团体总分排列名次,在规定时间内每人踢个以上含个为优秀下表是甲班和乙班成绩最好的名学生的比赛成绩单位:个
号 号 号 号 号 总数
甲班
乙班
经统计发现,两班名学生踢毽子的总个数相等此时有学生建议,可以考查数据的其他信息作为参考请你回答下列问题:
求甲、乙两班名学生比赛成绩的中位数.
计算甲、乙两班名学生比赛成绩的方差,并比较哪一个方差小.
根据以上信息,你认为哪个班获得冠军简述理由.
24.本小题分
某校舞蹈队共名学生,测量并获取了所有学生的身高单位:,数据整理如下:
名学生的 身高:
,,,,,,,,
,,,,,,,
名学生的身高的平均数、中位数、众数:
平均数 中位数 众数
写出表中,的值;
对于不同组的学生,如果一组学生的身高的方差越小,则认为该组舞台呈现效果越好.据此推断:在下列两组学生中,舞台呈现效果更好的是______填“甲组”或“乙组”;
甲组学生的身高
乙组学生的身高
该舞蹈队要选五名学生参加比赛.已确定三名学生参赛,他们的身高分别为,,,他们的身高的方差为在选另外两名学生时,首先要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的方差小于,其次要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的平均数尽可能大,则选出的另外两名学生的身高分别为______和______.
25.本小题分
“惜餐为荣,殄物为耻”,为了解落实“光盘行动”的情况,某校数学兴趣小组的同学调研了七、八年级部分班级某一天的餐厨垃圾质量从七、八年级中各随机抽取个班的餐厨垃圾质量的数据单位:,进行整理和分析餐厨垃圾质量用表示,共分为四个等级:,,,,下面给出了部分信息.
七年级个班的餐厨垃圾质量:,,,,,,,,,.
八年级个班的餐厨垃圾质量中等级包含的所有数据为:,,,,.
七、八年级抽取的班级餐厨垃圾质量统计表
年级 平均数 中位数 众数 方差 等级所占百分比
七年级
八年级
根据以上信息,解答下列问题:
直接写出上述表中,,的值;
该校八年级共个班,估计八年级这一天餐厨垃圾质量符合等级的班级数;
根据以上数据,你认为该校七、八年级的“光盘行动”,哪个年级落实得更好?请说明理由写出一条理由即可.
答案和解析
1.【答案】
【解析】解:设成绩为环的人数是,根据题意,得:
,解得,
经检验是分式方程的解,且符合题意.
2.【答案】
【解析】根据题意,得,解得,经检验:是原分式方程的解,故选B.
3.【答案】
【解析】略
4.【答案】
【解析】解:、人,
参加本次植树活动共有人,选项A正确;
B、出现的次数最多,出现了次,
每人植树量的众数是棵,选项B正确;
C、共有个数,第、个数为,
每人植树量的中位数是棵,选项C正确;
D、棵,
每人植树量的平均数约是棵,选项D不正确.
故选:.
A、将人数进行相加,即可得出结论A正确;、由种植棵的人数最多,可得出结论B正确;、由,可得出每人植树量数列中第、个数为,即结论C正确;、利用加权平均数的计算公式,即可求出每人植树量的平均数约是棵,结论D错误.此题得解.
本题考查了条形统计图、中位数、众数以及加权平均数,逐一分析四个选项的正误是解题的关键.
5.【答案】
【解析】解:根据中位数的定义个整数从小到大排列时,其中位数为,前两个数不是众数,因而一定不是同一个数则前两位最大是,,
根据众数的定义可知后两位最大为,这个整数最大为:,,,,,
这个整数可能的最大的和是.
6.【答案】
【解析】略
7.【答案】
【解析】【分析】
本题考查了中位数与平均数,正确理解中位数与平均数的意义是解题的关键.
平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.将一组数据按照从小到大或从大到小的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
【解答】解:解这名学生参加公益劳动时间的平均数:,一定在之间,正确;
由统计表类别栏计算可得,各时间段人数分别为,,,,,则中位数在之间,故正确.
由统计表计算可得,初中学段栏的人数在大于等于小于等于之间,当人数为时中位数在之间;当人数为时,中位数在之间,故正确.
由统计表计算可得,高中学段栏各时间段人数分别为大于等于小于等于,,,,,当时间段人数为时,中位数在之间;当时间段人数为时,中位数在之间,故错误.
故选:.
8.【答案】
【解析】【分析】
本题考查方差的计算公式的运用:一般地设有个数据,,,,若每个数据都放大或缩小相同的倍数后再同加或同减去一个数,其平均数也有相对应的变化,方差则变为这个倍数的平方倍.根据如果将一组数据中的每一个数据都加上同一个非零常数,那么这组数据的波动情况不变,即方差不变,从而得出答案.
【解答】
解:一组数据中的每一个数据都加上或都减去同一个常数后,它的平均数都加上或都减去这一个常数,两数进行相减,故方差不变,
一组数据中的每一个数据都乘以或都除以同一个常数后,它的平均数都乘以或都除以这一个常数,两数进行相减,故方差成平方变化,
,,,,,,是在原数据,,,,,,中每个数均先乘以再加上,
数据,,,,,,的方差为数据,,,,,,的方差的倍.
故选D.
9.【答案】
【解析】平均数、中位数和众数不能说明某天新增疑似病例是否超过人,故A,C错误.
设连续天,每天新增疑似病例为,,,,,若有一天新增疑似病例超过人,假设为人,则,若方差是,说明连续天,每天新增疑似病例不超过人,故B正确.
当方差大于,方差的具体数值未知,不能确定数据的波动大小,故D错误.
故选B.
10.【答案】
【解析】略
11.【答案】
【解析】解:,
,
所以,,
从表格中可以看出,甲组的数据分布于,乙组的数据分布于,
根据方差的概念和意义可知,甲组的数据波动比乙组的数据波动更小,离散程度更小,稳定性也更大,
所以,
故答案为:.
先计算甲乙两组的平均数判断和的大小,再根据方差的概念和意义,分析和的大小,即可解答.
本题考查了方差和平均数,熟练掌握方差和平均数的相关知识,并结合题意加以分析是解题的关键.
12.【答案】
【解析】【分析】
本题考查加权平均数,解题的关键是掌握加权平均数的定义.
根据加权平均数的定义列式计算即可.
【解答】
解:该应聘者的总成绩是:分.
13.【答案】
【解析】略
14.【答案】平均数
中位数
众数
【解析】略
15.【答案】
【解析】由题意得解得即这两组数据为,,,和,,,这两组数合并成一组新数据为,,,,,,,在这组新数据中,出现次数最多的是,众数是.
16.【答案】
【解析】解:从图看出:乙组数据的波动较小,故乙的方差较小,即.
故答案为.
结合图形,根据数据波动较大的方差较大即可求解.
本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
17.【答案】【小题】
【小题】
【解析】 略
略
18.【答案】解:甲组的平均成绩为分,
乙组的平均成绩为分,
所以乙组第一名,甲组第二名.
甲组的平均成绩为分,
乙组的平均成绩为分,
所以甲组成绩最高.
【解析】略
19.【答案】解:根据题意得,
分,
,
八年级班会获得“先进班集体”称号.
【解析】略
20.【答案】解:甲厂: 乙厂: 丙厂:
甲家的销售广告利用了平均数表示集中趋势的特征数乙家的销售广告利用了众数表示集中趋势的特征数丙家的销售广告利用了中位数表示集中趋势的特征数.
平均数:乙大于丙大于甲众数:乙大于甲大于丙中位数:乙大于丙大于甲,顾客在选购产品时,一般以平均数为依据,选平均数大的厂家的产品,因此应选乙厂的产品.
【解析】略
21.【答案】解:这天内小申家每天用水量的平均数为升.
将这天的用水量从小到大重新排列为,,,,,,,
用水量的中位数为升.
,
答:第天小申家洗衣服的水占这一天总用水量的百分比为.
答案不唯一,例如:小申家冲厕所的用水量较大,可以用洗衣服的水冲厕所采用以上建议,每天可节约用水升,一个月估计可以节约用水升.
【解析】略
22.【答案】【小题】平均身高为
【小题】这名女生的身高的中位数是,众数是
【小题】答案不唯一如:可先将八年级身高为的所有女生挑选出来作为参
加方队的人选如果不够,则挑选身高与比较接近的女生,直至挑选
到人为止
【解析】 略
略
略
23.【答案】【小题】甲班:,乙班:
【小题】甲班:,乙班:甲班成绩的方差较小
【小题】略
【解析】 略
略
略
24.【答案】【小问详解】
解:将这组数据按照从小到大的顺序排列为:,,,,,,,,,,,,,,,,
出现次数最多的数是,出现了次,即众数,
个数据中的第和第个数据分别是,,
中位数,
,;
【小问详解】
解:甲组身高的平均数为,
甲组身高的方差为
乙组身高的平均数为,
乙组身高的方差为,
舞台呈现效果更好的是甲组,
故答案为:甲组;
【小问详解】
解:,,的平均数为
所选的两名学生与已确定的三名学生所组成的五名学生的身高的方差小于,
数据的差别较小,数据才稳定,
可供选择的有:,,
且选择,时,平均数会增大,
故答案为:,.
【解析】【分析】根据中位数和众数的定义求解即可;
计算每一组的方差,根据方差越小数据越稳定进行判断即可;
根据要求,身高的平均数尽可能大且方差小于,结合其余学生的身高即可做出选择.
25.【答案】解:,,;
八年级抽测的个班级中,等级的百分比是.
估计该校八年级共个班这一天餐厨垃圾质量符合等级的班级数为:个.
答:该校八年级共个班,估计八年级这一天餐厨垃圾质量符合等级的班级数为个.
七年级各班落实“光盘行动”更好,因为:
七年级各班餐厨垃圾质量众数,低于八年级各班餐厨质量垃圾的众数.
七年级各班餐厨垃圾质量等级的高于八年级各班餐厨质量垃圾质量等级的.
八年级各班落实“光盘行动”更好,因为:
八年级各班餐厨垃圾质量的中位数低于七年级各班餐厨质量垃圾的中位数.
八年级各班餐厨垃圾质量的方差低于七年级各班餐厨质量垃圾的方差,更稳定.
【解析】本题考查了中位数、众数、方差的意义,关键在于根据图中信息结合统计相关知识的意义进行分析即可.
在,,,,,,,,,中,出现次数最多的是,
众数,
八年级个班中等级有个,占,、等级所占百分比分别为、,
等级占:,即,
把八年级个班的餐厨垃圾质量从小到大排列,、等级共占个数,则第个和第个数都是等级中的,
,
故答案为:,,;
用抽测的百分比乘总体即可求解.
从众数,中位数、等级的百分比、方差进行评论即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙教版初中数学八年级下册第三单元《数据分析初步》单元测试卷
考试范围:第三单元;考试时间:120分钟;总分:120分
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.某次射击训练中,一小组的成绩如表所示:已知该小组的平均成绩为环,那么成绩为环的人数是
( )
环数
人数
A. 人 B. 人 C. 人 D. 人
2.某工厂生产质量分别为,,,四种规格的球,现从中取个球装到一个空箱子里,这时箱子里球的平均质量为,若再放入一个的球,此时箱子里球的平均质量变为,则的值为
( )
A. B. C. D.
3.一个小组有名学生,如果名学生的平均成绩是分,另外名学生每人得分,那么整个小组的平均成绩是( )
A. 分 B. 分 C. 分 D. 分
4.某单位组织职工开展植树活动,植树量与人数之间关系如图,下列说法不正确的是( )
A. 参加本次植树活动共有人 B. 每人植树量的众数是棵
C. 每人植树量的中位数是棵 D. 每人植树量的平均数是棵
5.当个整数从小到大排列,其中位数是,如果这个数集的唯一众数是,那么这个整数可能的最大的和是( )
A. B. C. D.
6.某班举办元旦联欢会,班长对全班同学最爱吃哪几种水果这一问题作了调查,班长在确定购买哪一种水果时,最值得关注的统计量是( )
A. 中位数. B. 平均数. C. 众数. D. 加权平均数.
7.某校共有名学生,为了解本学期学生参加公益劳动的情况,收集了他们参加公益劳动时间单位:小时等数据,以下是根据数据绘制的统计图表的一部分
时间
人数
学生类型
性别 男
女
学段 初中
高中
下面有四个推断:
这名学生参加公益劳动时间的平均数一定在之间
这名学生参加公益劳动时间的中位数在之间
这名学生中的初中生参加公益劳动时间的中位数一定在之间
这名学生中的高中生参加公益劳动时间的中位数可能在之间
所有合理推断的序号是( )
A. B. C. D.
8.若数据,,,,,,的方差是,则数据,,,,,,的方差是
( )
A. B. C. D.
9.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续天,每天新增疑似病例不超过人”下列新增疑似病例的数据中,一定符合该标志的是( )
A. 平均数是,中位数是 B. 平均数是,总体方差是
C. 中位数是,众数是 D. 平均数是,方差大于
10.在对一组样本数据进行分析时,小华列出了方差的计算公式:
.
由公式提供的信息,得到以下四个结论:样本的容量是;样本的中位数是;样本的众数是;样本的平均数是其中正确的是
( )
A. B. C. D.
11.某校在读书系列活动中,为了解学生的课外阅读情况,随机选取了八年级某班甲、乙两组学生一周的课外阅读时间单位:进行统计,数据如图表,两组数据的平均数分别为、,方差分别为、,则( )
甲组
乙组
A. , B. ,
C. , D. ,
12.家乐福超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如表:
测试项目 创新能力 综合知识 语言表达
测试成绩分数
将创新能力、综合知识和语言表达三项测试成绩按的比分计入总成绩,则该应聘者的总成绩是
分.( )
A. B. C. D. 以上都不对
二、填空题:本题共4小题,每小题3分,共12分。
13.棉农种植了一亩地的良种棉,这亩棉约种了株,在棉花采摘时,棉农随机确定了株棉花进行分摘,等采摘完后称这株棉花,产籽棉的质量如下表所示:
棉株数
单株产量
这株棉花的平均产量为 ,并根据计算估计这亩地的棉花产量是 亩,市制面积单位
14.从甲、乙、丙三个厂家生产的同一种产品中各抽取件,对它们的使用寿命进行跟踪调查,结果如下单位:年:
甲:,,,,,,,;
乙:,,,,,,,;
丙:,,,,,,,.
三个厂家在广告中都称该产品的使用寿命是年.请根据结果判断,厂家在广告中分别运用了平均数、众数、中位数中的哪一种集中趋势的特征数:甲: ,乙: ,丙: .
15.两组数据:,,,与,,的平均数都是若将这两组数据合并为一组新数据,则这组新数据的众数为 .
16.将甲、乙两组各个数据绘制成折线统计图如图,两组数据的平均数都是,设甲、乙两组数据的方差分别为则 填“”“”或“”.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
为了响应“五水共治,建设美丽家园”的号召,某小区业委会随机调查了该小区户家庭月的用水量,结果如下表所示:
月用水量
户数
计算这户家庭月的平均用水量.
若该小区有户家庭,估计该小区月的用水量为多少吨?
18.本小题分
某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛现有甲、乙两个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录甲、乙两个小组各项得分如下表:
小组 研究报告 小组展示 答辩
甲
乙
计算各小组的平均成绩,并从高分到低分确定小组的排名顺序
如果研究报告、小组展示、答辩按照计算成绩,哪个小组的成绩最高
19.本小题分
某学校评选先进班集体,从“学习”“卫生”“纪律”“活动参与”四个方面考核打分,各项满分均为分,所占比例如下表:
项目 学习 卫生 纪律 活动参与
所占比例
八年级班这四项得分依次为,,,,若学校规定班级四项综合得分超过分的将会获得“先进班集体”称号,请你通过计算说明该班是否会获得“先进班集体”称号
20.本小题分
甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下:单位:年
甲厂:,,,,,,,,,
乙厂:,,,,,,,,,
丙厂:,,,,,,,,,
请回答下面问题:
填空:
平均数 众数 中位数
甲厂
乙厂
丙厂
这三个厂家的销售广告分别利用了哪一种表示集中趋势的特征数
你是顾客,你买三家中哪一家的电子产品为什么
21.本小题分
为提高节水意识,小申随机统计了自己家天的用水量,并分析了第天的用水情况,将得到的数据进行整理后,绘制成统计图单位:升
求这天内小申家每天用水量的平均数和中位数.
求第天小申家洗衣服的水占这一天总用水量的百分比.
请你根据统计图中的信息,给小申家提出一条合理的节约用水建议,并估算采用你的建议后小申家一个月按天计算节约的用水量.
22.本小题分
下表是从某校八年级名女生中随机抽取的名女生的身高统计表.
身高
人数
依据样本,估计该校八年级女生的平均身高.
写出这名女生身高的中位数和众数.
请你依据这个样本,设计一个挑选名女生组成方队的方案要求选中女生的身高尽可能接近
23.本小题分
希望中学八年级学生开展踢毽子活动,每班派名学生参加,按团体总分排列名次,在规定时间内每人踢个以上含个为优秀下表是甲班和乙班成绩最好的名学生的比赛成绩单位:个
号 号 号 号 号 总数
甲班
乙班
经统计发现,两班名学生踢毽子的总个数相等此时有学生建议,可以考查数据的其他信息作为参考请你回答下列问题:
求甲、乙两班名学生比赛成绩的中位数.
计算甲、乙两班名学生比赛成绩的方差,并比较哪一个方差小.
根据以上信息,你认为哪个班获得冠军简述理由.
24.本小题分
某校舞蹈队共名学生,测量并获取了所有学生的身高单位:,数据整理如下:
名学生的 身高:
,,,,,,,,
,,,,,,,
名学生的身高的平均数、中位数、众数:
平均数 中位数 众数
写出表中,的值;
对于不同组的学生,如果一组学生的身高的方差越小,则认为该组舞台呈现效果越好.据此推断:在下列两组学生中,舞台呈现效果更好的是______填“甲组”或“乙组”;
甲组学生的身高
乙组学生的身高
该舞蹈队要选五名学生参加比赛.已确定三名学生参赛,他们的身高分别为,,,他们的身高的方差为在选另外两名学生时,首先要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的方差小于,其次要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的平均数尽可能大,则选出的另外两名学生的身高分别为______和______.
25.本小题分
“惜餐为荣,殄物为耻”,为了解落实“光盘行动”的情况,某校数学兴趣小组的同学调研了七、八年级部分班级某一天的餐厨垃圾质量从七、八年级中各随机抽取个班的餐厨垃圾质量的数据单位:,进行整理和分析餐厨垃圾质量用表示,共分为四个等级:,,,,下面给出了部分信息.
七年级个班的餐厨垃圾质量:,,,,,,,,,.
八年级个班的餐厨垃圾质量中等级包含的所有数据为:,,,,.
七、八年级抽取的班级餐厨垃圾质量统计表
年级 平均数 中位数 众数 方差 等级所占百分比
七年级
八年级
根据以上信息,解答下列问题:
直接写出上述表中,,的值;
该校八年级共个班,估计八年级这一天餐厨垃圾质量符合等级的班级数;
根据以上数据,你认为该校七、八年级的“光盘行动”,哪个年级落实得更好?请说明理由写出一条理由即可.
答案和解析
1.【答案】
【解析】解:设成绩为环的人数是,根据题意,得:
,解得,
经检验是分式方程的解,且符合题意.
2.【答案】
【解析】根据题意,得,解得,经检验:是原分式方程的解,故选B.
3.【答案】
【解析】略
4.【答案】
【解析】解:、人,
参加本次植树活动共有人,选项A正确;
B、出现的次数最多,出现了次,
每人植树量的众数是棵,选项B正确;
C、共有个数,第、个数为,
每人植树量的中位数是棵,选项C正确;
D、棵,
每人植树量的平均数约是棵,选项D不正确.
故选:.
A、将人数进行相加,即可得出结论A正确;、由种植棵的人数最多,可得出结论B正确;、由,可得出每人植树量数列中第、个数为,即结论C正确;、利用加权平均数的计算公式,即可求出每人植树量的平均数约是棵,结论D错误.此题得解.
本题考查了条形统计图、中位数、众数以及加权平均数,逐一分析四个选项的正误是解题的关键.
5.【答案】
【解析】解:根据中位数的定义个整数从小到大排列时,其中位数为,前两个数不是众数,因而一定不是同一个数则前两位最大是,,
根据众数的定义可知后两位最大为,这个整数最大为:,,,,,
这个整数可能的最大的和是.
6.【答案】
【解析】略
7.【答案】
【解析】【分析】
本题考查了中位数与平均数,正确理解中位数与平均数的意义是解题的关键.
平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.将一组数据按照从小到大或从大到小的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
【解答】解:解这名学生参加公益劳动时间的平均数:,一定在之间,正确;
由统计表类别栏计算可得,各时间段人数分别为,,,,,则中位数在之间,故正确.
由统计表计算可得,初中学段栏的人数在大于等于小于等于之间,当人数为时中位数在之间;当人数为时,中位数在之间,故正确.
由统计表计算可得,高中学段栏各时间段人数分别为大于等于小于等于,,,,,当时间段人数为时,中位数在之间;当时间段人数为时,中位数在之间,故错误.
故选:.
8.【答案】
【解析】【分析】
本题考查方差的计算公式的运用:一般地设有个数据,,,,若每个数据都放大或缩小相同的倍数后再同加或同减去一个数,其平均数也有相对应的变化,方差则变为这个倍数的平方倍.根据如果将一组数据中的每一个数据都加上同一个非零常数,那么这组数据的波动情况不变,即方差不变,从而得出答案.
【解答】
解:一组数据中的每一个数据都加上或都减去同一个常数后,它的平均数都加上或都减去这一个常数,两数进行相减,故方差不变,
一组数据中的每一个数据都乘以或都除以同一个常数后,它的平均数都乘以或都除以这一个常数,两数进行相减,故方差成平方变化,
,,,,,,是在原数据,,,,,,中每个数均先乘以再加上,
数据,,,,,,的方差为数据,,,,,,的方差的倍.
故选D.
9.【答案】
【解析】平均数、中位数和众数不能说明某天新增疑似病例是否超过人,故A,C错误.
设连续天,每天新增疑似病例为,,,,,若有一天新增疑似病例超过人,假设为人,则,若方差是,说明连续天,每天新增疑似病例不超过人,故B正确.
当方差大于,方差的具体数值未知,不能确定数据的波动大小,故D错误.
故选B.
10.【答案】
【解析】略
11.【答案】
【解析】解:,
,
所以,,
从表格中可以看出,甲组的数据分布于,乙组的数据分布于,
根据方差的概念和意义可知,甲组的数据波动比乙组的数据波动更小,离散程度更小,稳定性也更大,
所以,
故答案为:.
先计算甲乙两组的平均数判断和的大小,再根据方差的概念和意义,分析和的大小,即可解答.
本题考查了方差和平均数,熟练掌握方差和平均数的相关知识,并结合题意加以分析是解题的关键.
12.【答案】
【解析】【分析】
本题考查加权平均数,解题的关键是掌握加权平均数的定义.
根据加权平均数的定义列式计算即可.
【解答】
解:该应聘者的总成绩是:分.
13.【答案】
【解析】略
14.【答案】平均数
中位数
众数
【解析】略
15.【答案】
【解析】由题意得解得即这两组数据为,,,和,,,这两组数合并成一组新数据为,,,,,,,在这组新数据中,出现次数最多的是,众数是.
16.【答案】
【解析】解:从图看出:乙组数据的波动较小,故乙的方差较小,即.
故答案为.
结合图形,根据数据波动较大的方差较大即可求解.
本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
17.【答案】【小题】
【小题】
【解析】 略
略
18.【答案】解:甲组的平均成绩为分,
乙组的平均成绩为分,
所以乙组第一名,甲组第二名.
甲组的平均成绩为分,
乙组的平均成绩为分,
所以甲组成绩最高.
【解析】略
19.【答案】解:根据题意得,
分,
,
八年级班会获得“先进班集体”称号.
【解析】略
20.【答案】解:甲厂: 乙厂: 丙厂:
甲家的销售广告利用了平均数表示集中趋势的特征数乙家的销售广告利用了众数表示集中趋势的特征数丙家的销售广告利用了中位数表示集中趋势的特征数.
平均数:乙大于丙大于甲众数:乙大于甲大于丙中位数:乙大于丙大于甲,顾客在选购产品时,一般以平均数为依据,选平均数大的厂家的产品,因此应选乙厂的产品.
【解析】略
21.【答案】解:这天内小申家每天用水量的平均数为升.
将这天的用水量从小到大重新排列为,,,,,,,
用水量的中位数为升.
,
答:第天小申家洗衣服的水占这一天总用水量的百分比为.
答案不唯一,例如:小申家冲厕所的用水量较大,可以用洗衣服的水冲厕所采用以上建议,每天可节约用水升,一个月估计可以节约用水升.
【解析】略
22.【答案】【小题】平均身高为
【小题】这名女生的身高的中位数是,众数是
【小题】答案不唯一如:可先将八年级身高为的所有女生挑选出来作为参
加方队的人选如果不够,则挑选身高与比较接近的女生,直至挑选
到人为止
【解析】 略
略
略
23.【答案】【小题】甲班:,乙班:
【小题】甲班:,乙班:甲班成绩的方差较小
【小题】略
【解析】 略
略
略
24.【答案】【小问详解】
解:将这组数据按照从小到大的顺序排列为:,,,,,,,,,,,,,,,,
出现次数最多的数是,出现了次,即众数,
个数据中的第和第个数据分别是,,
中位数,
,;
【小问详解】
解:甲组身高的平均数为,
甲组身高的方差为
乙组身高的平均数为,
乙组身高的方差为,
舞台呈现效果更好的是甲组,
故答案为:甲组;
【小问详解】
解:,,的平均数为
所选的两名学生与已确定的三名学生所组成的五名学生的身高的方差小于,
数据的差别较小,数据才稳定,
可供选择的有:,,
且选择,时,平均数会增大,
故答案为:,.
【解析】【分析】根据中位数和众数的定义求解即可;
计算每一组的方差,根据方差越小数据越稳定进行判断即可;
根据要求,身高的平均数尽可能大且方差小于,结合其余学生的身高即可做出选择.
25.【答案】解:,,;
八年级抽测的个班级中,等级的百分比是.
估计该校八年级共个班这一天餐厨垃圾质量符合等级的班级数为:个.
答:该校八年级共个班,估计八年级这一天餐厨垃圾质量符合等级的班级数为个.
七年级各班落实“光盘行动”更好,因为:
七年级各班餐厨垃圾质量众数,低于八年级各班餐厨质量垃圾的众数.
七年级各班餐厨垃圾质量等级的高于八年级各班餐厨质量垃圾质量等级的.
八年级各班落实“光盘行动”更好,因为:
八年级各班餐厨垃圾质量的中位数低于七年级各班餐厨质量垃圾的中位数.
八年级各班餐厨垃圾质量的方差低于七年级各班餐厨质量垃圾的方差,更稳定.
【解析】本题考查了中位数、众数、方差的意义,关键在于根据图中信息结合统计相关知识的意义进行分析即可.
在,,,,,,,,,中,出现次数最多的是,
众数,
八年级个班中等级有个,占,、等级所占百分比分别为、,
等级占:,即,
把八年级个班的餐厨垃圾质量从小到大排列,、等级共占个数,则第个和第个数都是等级中的,
,
故答案为:,,;
用抽测的百分比乘总体即可求解.
从众数,中位数、等级的百分比、方差进行评论即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
